Computation Binary Numbers Decimal numbers 905 Binary numbers

Computation

Binary Numbers • Decimal numbers 905 • Binary numbers 1110001001
Counting in Binary http: //www. youtube. com/watch? v=z. ELAfmp 3 f. XY
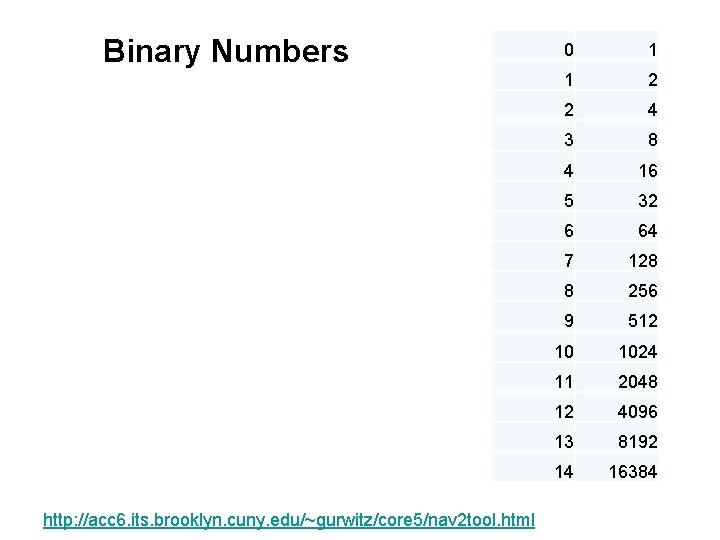
Binary Numbers http: //acc 6. its. brooklyn. cuny. edu/~gurwitz/core 5/nav 2 tool. html 0 1 1 2 2 4 3 8 4 16 5 32 6 64 7 128 8 256 9 512 10 1024 11 2048 12 4096 13 8192 14 16384

Text Computers have revolutionized our world. They have changed the course of our daily lives, the way we do science, the way we entertain ourselves, the way that business is conducted, and the way we protect our security.

Text Computers have revolutionized our world. They have changed the course of our daily lives, the way we do science, the way we entertain ourselves, the way that business is conducted, and the way we protect our security. Les ordinateurs ont révolutionné notre monde. Ils ont changé le cours de notre vie quotidienne, notre façon de faire la science, la façon dont nous divertissons, la façon dont les affaires sont menées, et la façon dont nous protégeons notre sécurité.

Text Computers have revolutionized our world. They have changed the course of our daily lives, the way we do science, the way we entertain ourselves, the way that business is conducted, and the way we protect our security. Les ordinateurs ont révolutionné notre monde. Ils ont changé le cours de notre vie quotidienne, notre façon de faire la science, la façon dont nous divertissons, la façon dont les affaires sont menées, et la façon dont nous protégeons notre sécurité. 計算機已經徹底改變我們的世界。當然,他們已經改變了我 們的日常生活中,我們這樣做科研,我們自娛自樂的方式, 經營的方式進行的方式,以及我們保護我們的安全。

Representing Text • Decide how many characters we need to represent. • Determine the required number of bits. • Ascii: 7 bits. Can encode 27 = 128 different symbols.
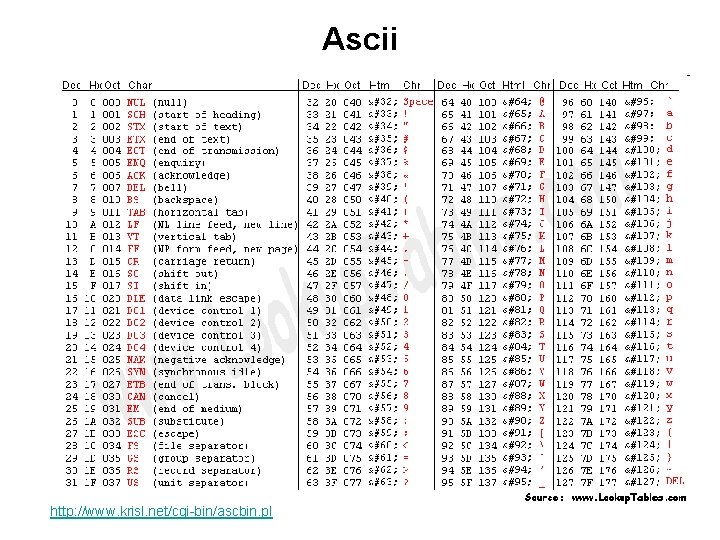
Ascii http: //www. krisl. net/cgi-bin/ascbin. pl

Representing Text F o u r 010001101111 01110101 01110010

Representing Text T h e n u m b e r i s 1 7 . 54 68 65 20 6 E 75 6 D 62 65 72 20 69 73 20 31 37 2 E

When We Need More Characters What about things like: 简体字

When We Need More Characters What about things like: 简体字 Answer: Unicode: 32 bits. Over 4 million characters. http: //www. unicode. org/charts/ A conversion applet: http: //www. pinyin. info/tools/converter/chars 2 uninumbers. html

But What Do Symbols Look Like? Computers have revolutionized our world.

The Basic Idea results = google(text, query)

The Basic Idea results = google(text, query) if word_count(text) > 5000: return(“Done!!”) else: return(“No sleep yet. ”)

The Basic Idea results = google(text, query) if word_count(text) > 5000: return(“Done!!”) else: return(“No sleep yet. ” display = render(text, font)

The Basic Idea Computers have revolutionized our world.

Digital Images

Pixels

Pixels Now we must turn this 2 -dimensional bit matrix into a string of bits.
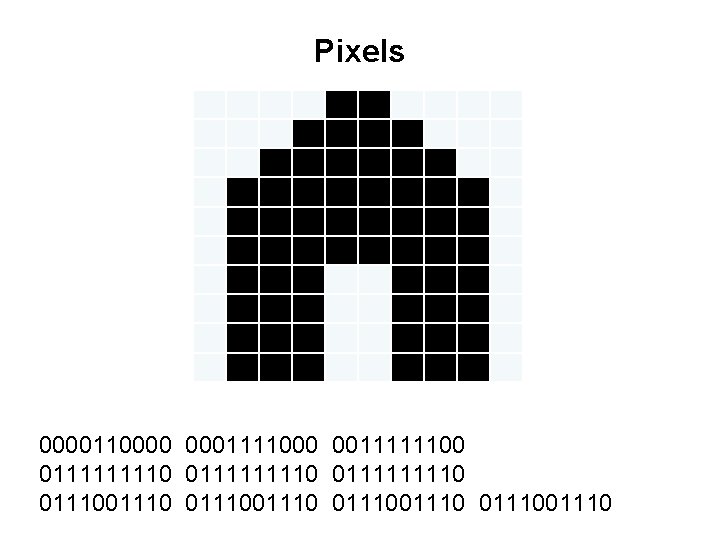
Pixels 0000110000 0001111000 0011111100 0111111110 011110 0111001110

Digital Images
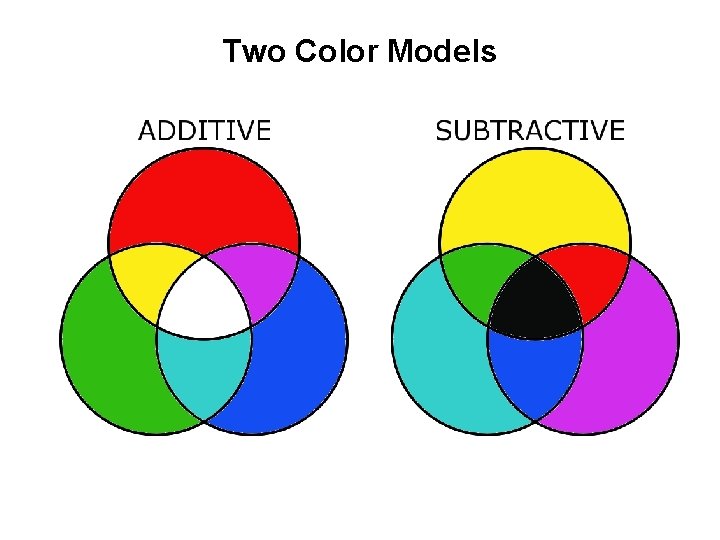
Two Color Models

RGB The red channel

RGB The green channel

RGB Red Green Blue

Experimenting with RGB http: //www. jgiesen. de/Color. Theory/RGBColor. Applet/rgbcolorapplet. html
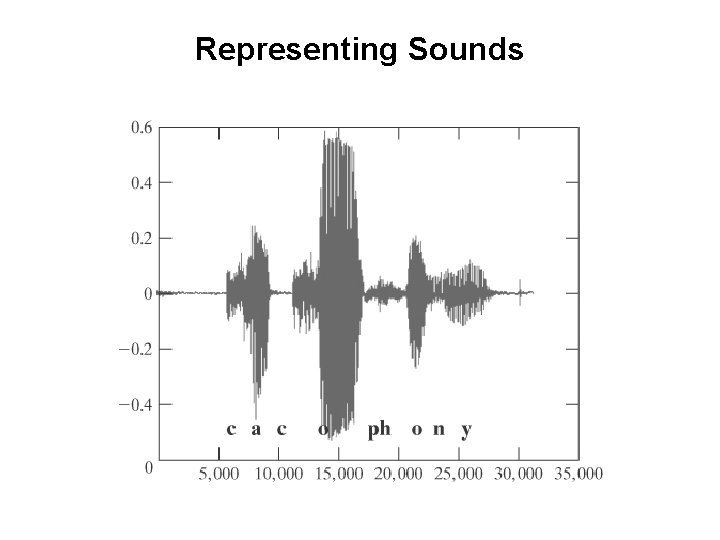
Representing Sounds
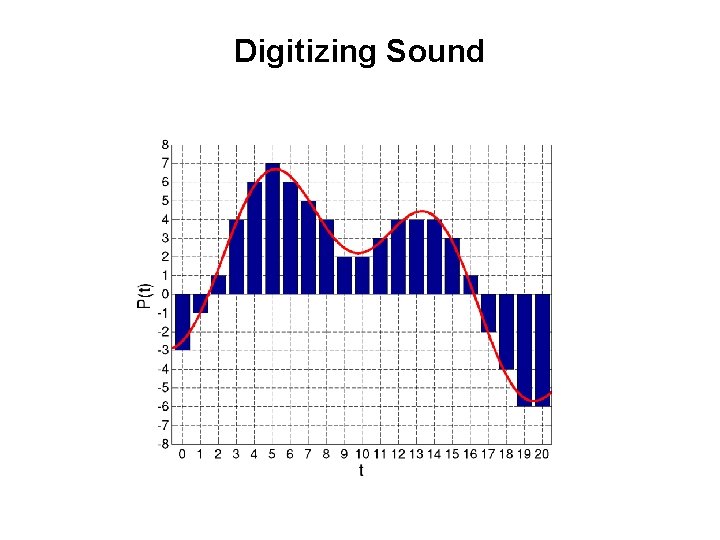
Digitizing Sound

Video

Representing Programs public static Tree. Map<String, Integer> create() throws IOException { Integer freq; String word; Tree. Map<String, Integer> result = new Tree. Map<String, Integer>(); JFile. Chooser c = new JFile. Chooser(); int retval = c. show. Open. Dialog(null); if (retval == JFile. Chooser. APPROVE_OPTION) { Scanner s = new Scanner( c. get. Selected. File()); while( s. has. Next() ) { word = s. next(). to. Lower. Case(); freq = result. get(word); result. put(word, (freq == null ? 1 : freq + 1)); } } return result; } }

Chess Boards Forsythe-Edwards Notation rnbqkbnr/pppp/8/8/PPPP/RNBQKBNR w KQkq - 0 1 http: //en. wikipedia. org/wiki/Forsyth-Edwards_Notation
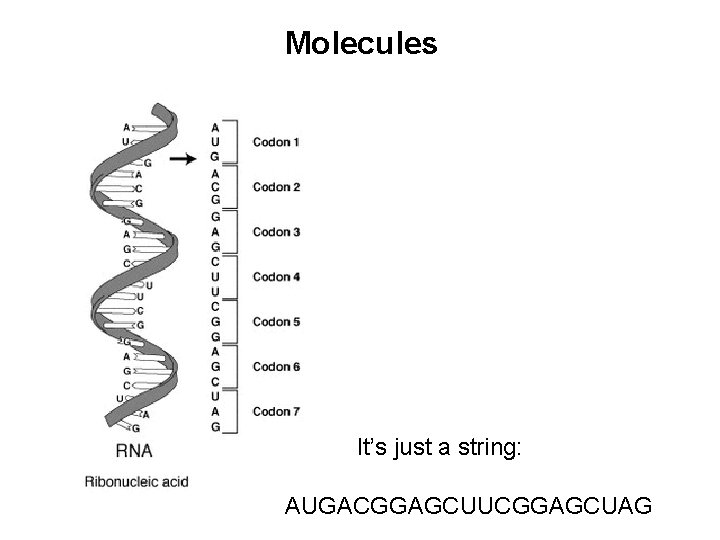
Molecules It’s just a string: AUGACGGAGCUUCGGAGCUAG

The Roots of Modern Technology 1834 Charles Babbage’s Analytical Engine Ada writes of the engine, “The Analytical Engine has no pretensions whatever to originate anything. It can do whatever we know how to order it to perform. ” The picture is of a model built in the late 1800 s by Babbage’s son from Babbage’s drawings.

Using Logic • Tai. Shan. Has. Tail • Smoky. Has. Tail • Puffy. Has. Tail • Chumpy. Has. Tail • Snowflake. Has. Tail

Using Logic • Tai. Shan. Has. Tail • Smoky. Has. Tail • Puffy. Has. Tail • Chumpy. Has. Tail • Snowflake. Has. Tail

Using Logic • Panda(Tai. Shan). • Bear(Smoky). • x (Panda(x) Bear(x). • x (Bear(x) Has. Part(x, Tail)). • x (Bear(x) Animal(x)). • x (Animal(x) Bear(x)). • x (Animal(x) y (Mother-of(y, x))). • x ((Animal(x) Dead(x)) Alive(x)). Does Tai. Shan have a tail?

Search Start state Goal state http: //www. javaonthebrain. com/java/puzz 15/

What is a Heuristic?

What is a Heuristic? The word heuristic comes from the Greek word (heuriskein), meaning “to discover”, which is also the origin of eureka, derived from Archimedes’ reputed exclamation, heurika (“I have found”), uttered when he had discovered that the volume of water displaced in the bath equals the volume of whatever (him) got put in the water. This could be used as a method for determining the purity of gold.

What is a Heuristic? The word heuristic comes from the Greek word (heuriskein), meaning “to discover”, which is also the origin of eureka, derived from Archimedes’ reputed exclamation, heurika (“I have found”), uttered when he had discovered that the volume of water displaced in the bath equals the volume of whatever (him) got put in the water. This could be used as a method for determining the purity of gold. A heuristic is a rule that helps us find something.

An Aside on Checking Facts on the Web Who invented the 15 -puzzle? Sam Loyd did: (http: //www. jimloy. com/puzz/15. htm ) Did he or didn’t he: (http: //www. archimedes-lab. org/game_slide 15/slide 15_puzzle. html ) No he didn’t: (http: //www. cut-the-knot. org/pythagoras/fifteen. shtml )
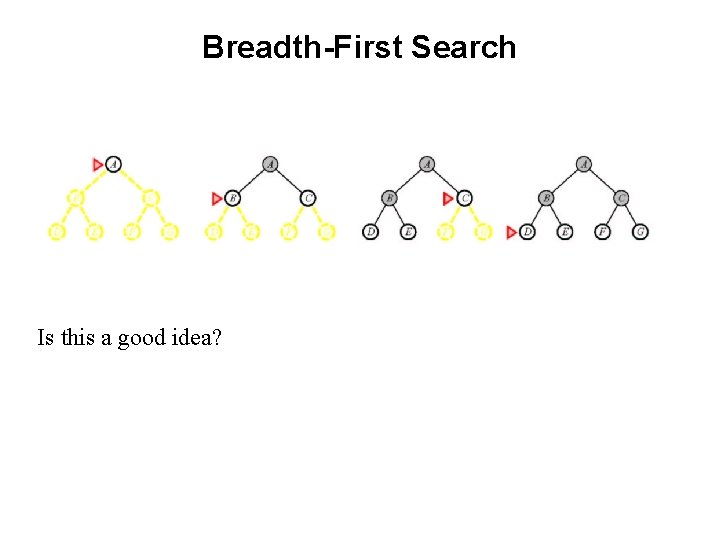
Breadth-First Search Is this a good idea?

Depth-First Search
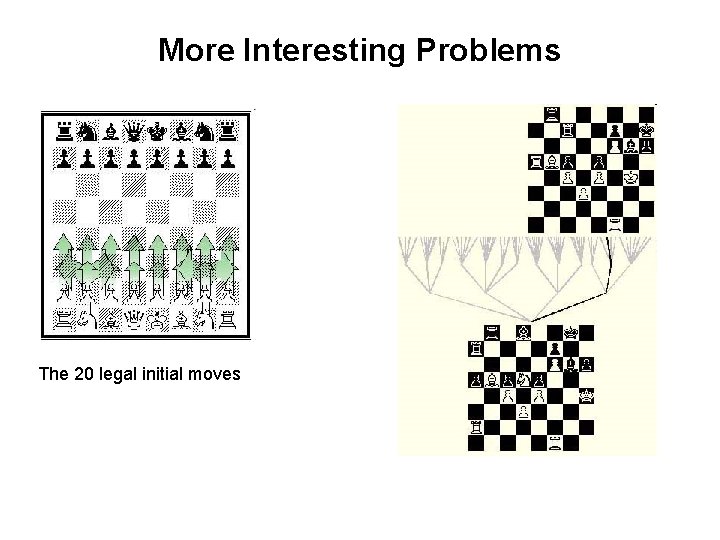
More Interesting Problems The 20 legal initial moves

Scalability Solving hard problems requires search in a large space. To play master-level chess requires searching about 8 ply deep. So about 358 or 2 1012 nodes must be examined.
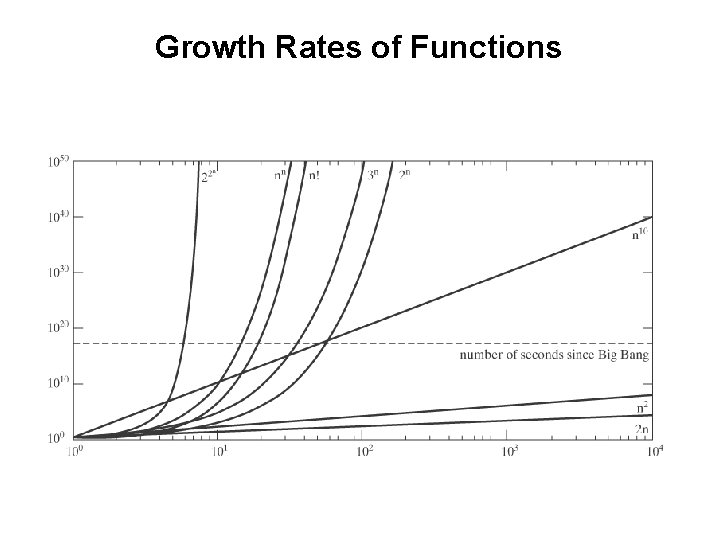
Growth Rates of Functions

Scalability To play one master-level game 2 1012 nodes Seconds since Big Bang 3 1017 Number of sequential games 150, 000 since Big Bang

Yet This Exists How?

A Heuristic Function for Chess c 1 c 2 c 3 c 4 * * material + mobility + king safety + center control +. . . Computing material: Pawn Knight Bishop Rook Queen King 100 325 500 975 32767

The Advent of the Computer 1945 ENIAC The first electronic digital computer 1948 Modified to be a stored program machine

1949 EDVAC Possibly the first stored program computer

Moore’s Law http: //www. intel. com/technology/mooreslaw/
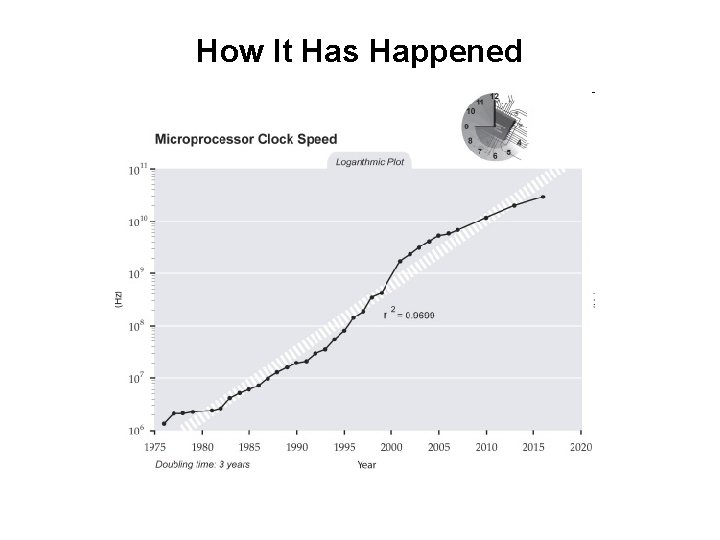
How It Has Happened
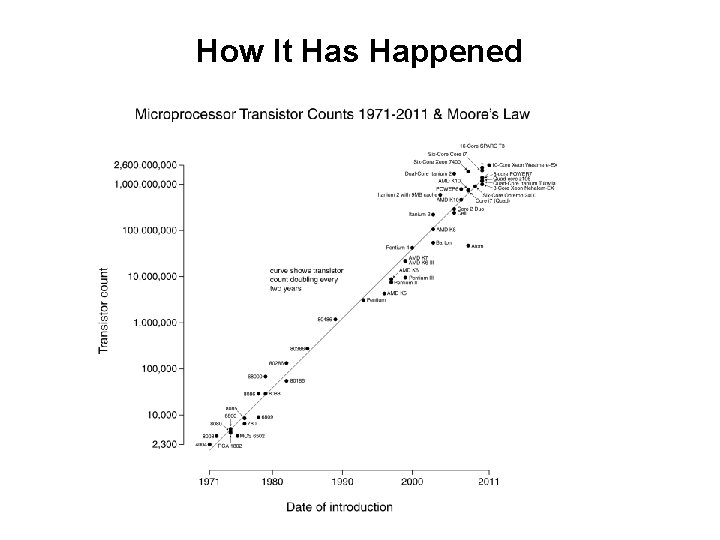
How It Has Happened

Can This Trend Continue? http: //www. nytimes. com/2010/08/31/science/31 compute. html? _r=1
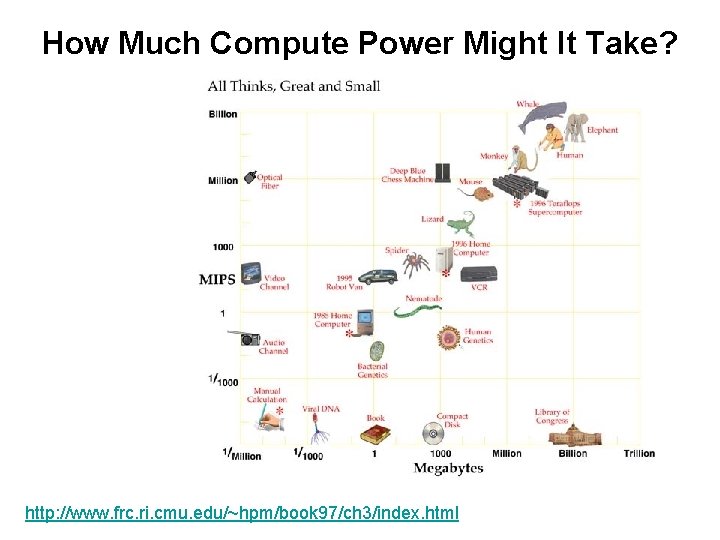
How Much Compute Power Might It Take? http: //www. frc. ri. cmu. edu/~hpm/book 97/ch 3/index. html
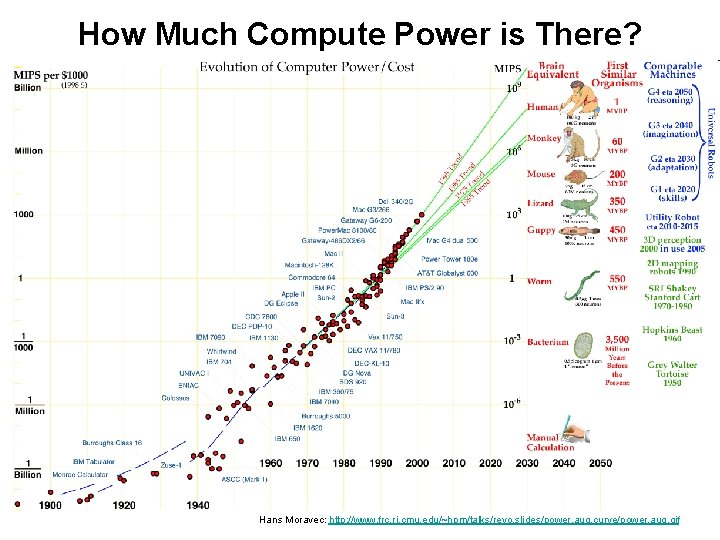
How Much Compute Power is There? Hans Moravec: http: //www. frc. ri. cmu. edu/~hpm/talks/revo. slides/power. aug. curve/power. aug. gif

How Much Compute Power Is There?

Kurweil’s Vision http: //www. pocket-lint. co. uk/news. phtml/12920/13944/Computersmatch-humans-by-2030. phtml

Some Other People Agree http: //www. networkworld. com/news/2009/092109 -intel-cto-interview. html

Countdown to Singularity
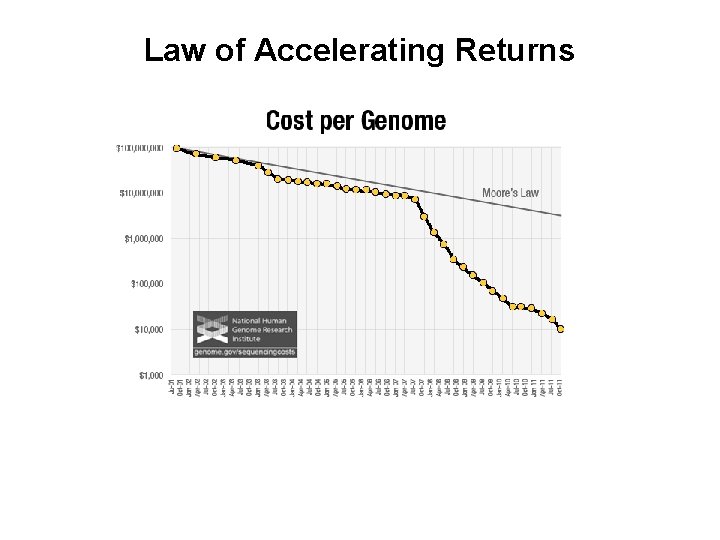
Law of Accelerating Returns

Limits to What We Can Compute Are there fundamentally uncomputable things? • Does God exist? • What’s the best way to run a country? • Does this puzzle have a solution?

What Can We Do? 1. Can we make all true statements theorems? 2. Can we decide whether a statement is a theorem?
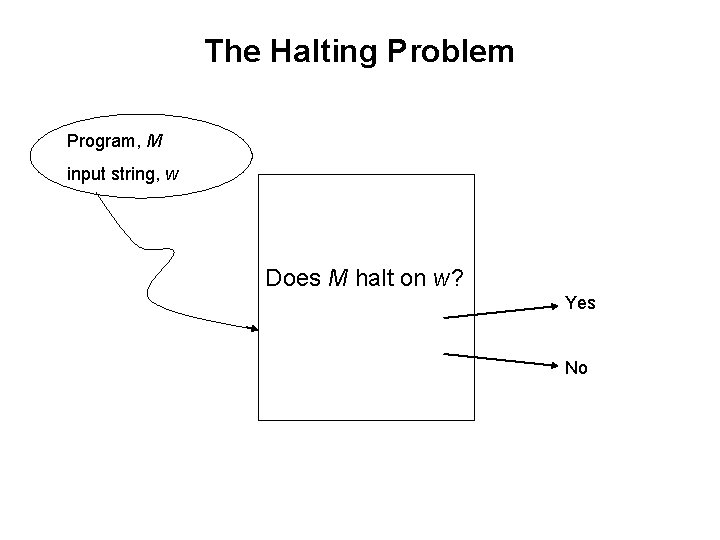
The Halting Problem Program, M input string, w Does M halt on w? Yes No

A Simple Example read name if name = “Elaine” then print “You win!!” else print “You lose ”

Another Example read number set result to 1 set counter to 2 until counter > number do set result to result * counter add 1 to counter print result

Programs Debug Programs Given an arbitrary program, can it be guaranteed to halt? read number set result to 1 set counter to 2 until counter > number do set result to result * counter add 1 to counter Suppose number = 5: print result number counter 1 5 2 2 5 3 6 5 4 24 5 5 120 5 6

Changing It a Bit Given an arbitrary program, can it be guaranteed to halt? read number set result to 1 set counter to 2 until counter > number do set number to number * counter add 1 to counter Suppose number = 5: print result number counter 1 5 2 1 10 3 1 30 4 1 120 5 1 600 6

How About this One? Does this program halt on all inputs? times 3(x: positive integer) = While x 1 do: If x is even then x = x/2. Else x = 3 x + 1. Let’s try it.
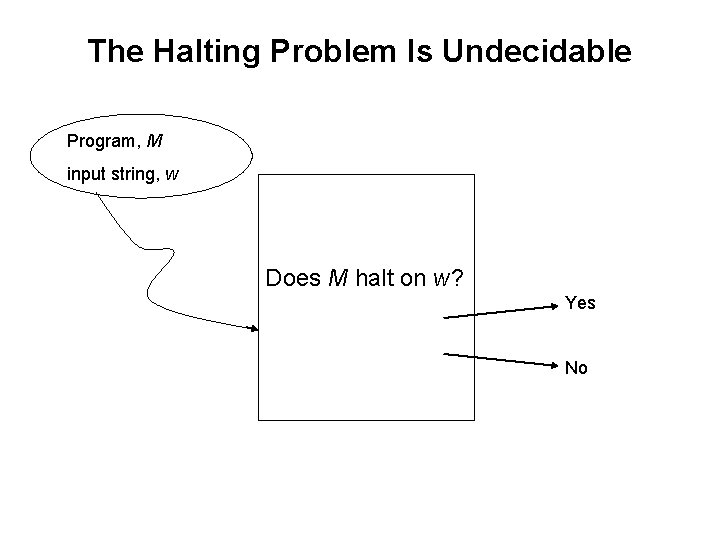
The Halting Problem Is Undecidable Program, M input string, w Does M halt on w? Yes No

Another Undecidable Problem The Post Correspondence Problem

A PCP Instance With a Simple Solution i X Y 1 b aab 2 abb b 3 aba a 4 baaa baba

A PCP Instance With a Simple Solution i X Y 1 b aab 2 abb b 3 aba a 4 baaa baba Solution: 3, 4, 1

Another PCP Instance i X Y 1 11 011 2 01 0 3 001 110
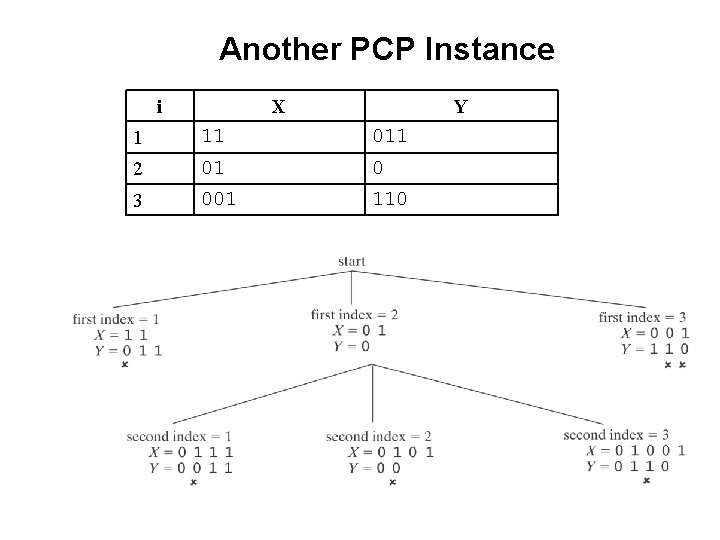
Another PCP Instance i X Y 1 11 011 2 01 0 3 001 110

The Post Correspondence Problem 1 2 3 List 1 ba abb bab List 2 bab bb abb

A PCP Instance With No Simple Solution i X Y 1 1101 1 2 0110 11 3 1 110

A PCP Instance With No Simple Solution i X Y 1 1101 1 2 0110 11 3 1 110 Shortest solution has length 252.

Can A Program Do This? Can we write a program to answer the following question: Given a PCP instance P, decide whether or not P has a solution. Return: True if it does. False if it does not.

What is a Program?

What is a Program? A procedure that can be performed by a computer.

The Post Correspondence Problem A program to solve this problem: Until a solution or a dead end is found do: If dead end, halt and report no. Generate the next candidate solution. Test it. If it is a solution, halt and report yes. So, if there are say 4 rows in the table, we’ll try: 1 2 3 4 1, 1 1, 2 1, 3 1, 4 1, 5 2, 1 …… 1, 1, 1 ….

Will This Work? • If there is a solution: • If there is no solution:
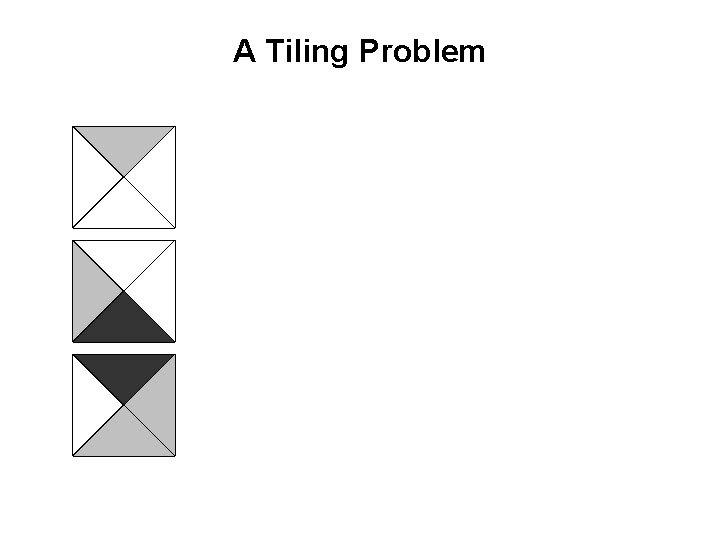
A Tiling Problem
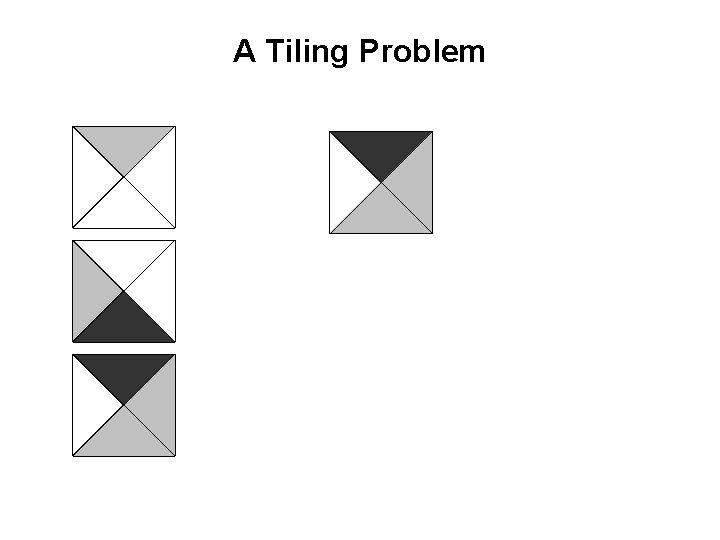
A Tiling Problem

A Tiling Problem
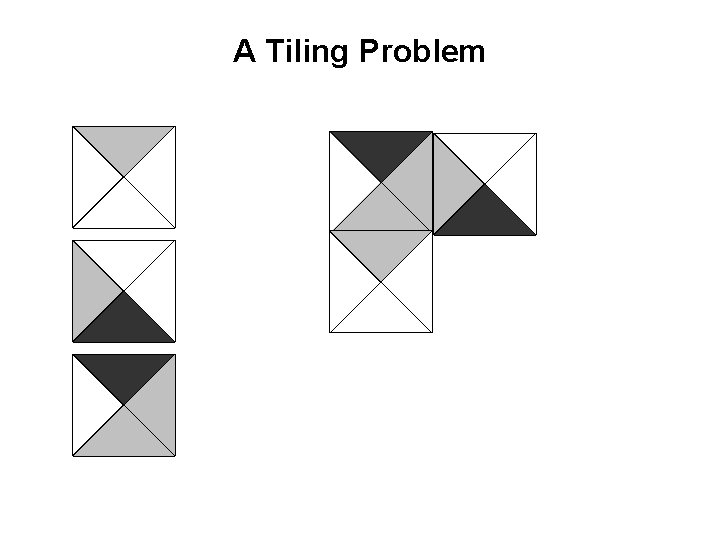
A Tiling Problem

A Tiling Problem
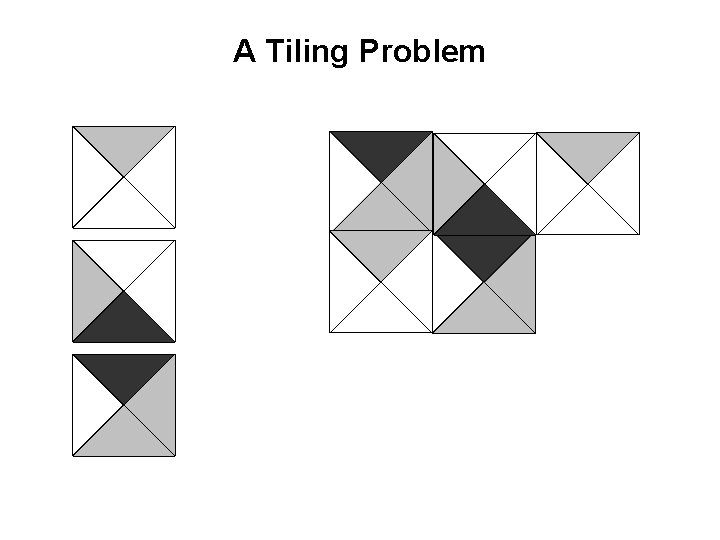
A Tiling Problem

A Tiling Problem
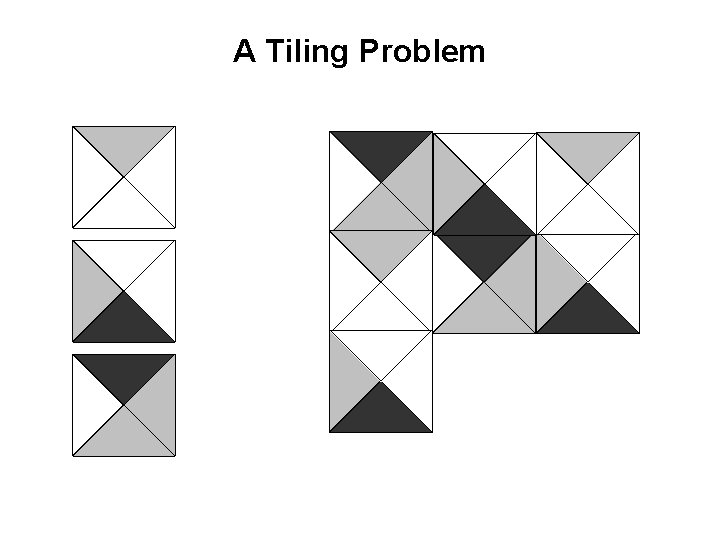
A Tiling Problem
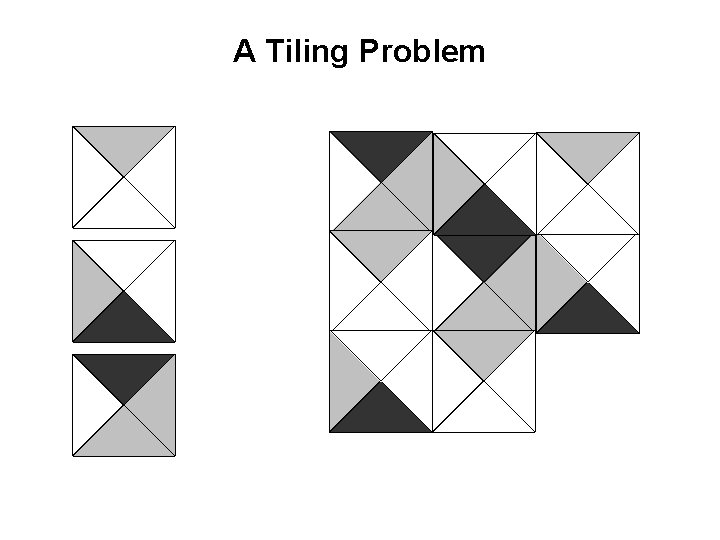
A Tiling Problem
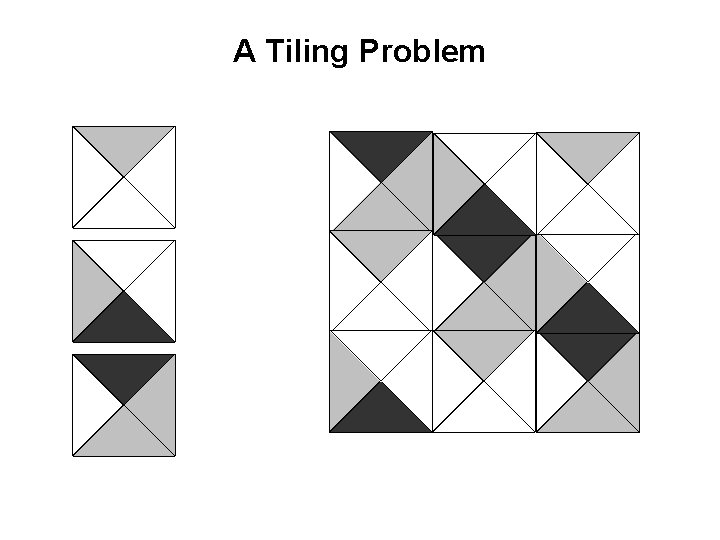
A Tiling Problem

Try This One
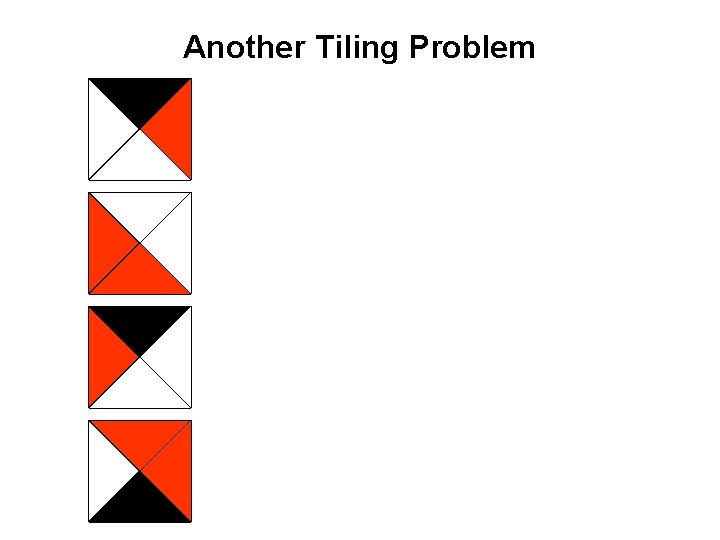
Another Tiling Problem
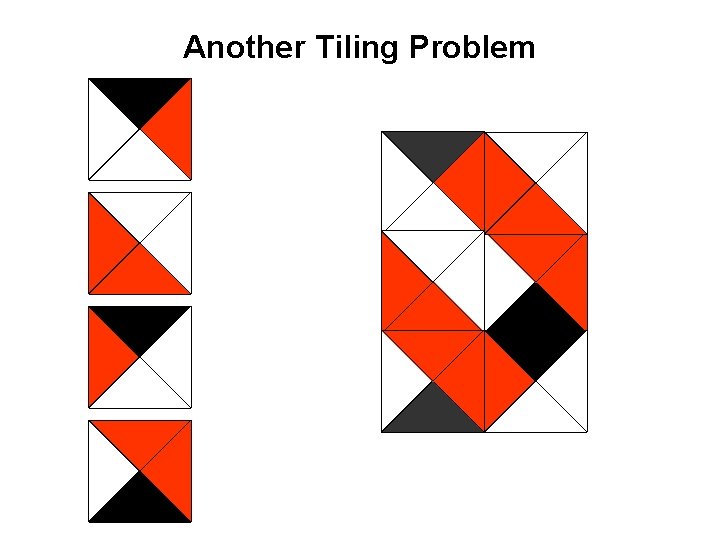
Another Tiling Problem

Is the Tiling Problem Decidable? Wang’s conjecture: If a given set of tiles can be used to tile an arbitrary surface, then it can always do so periodically. In other words, there must exist a finite area that can be tiled and then repeated infinitely often to cover any desired surface. But Wang’s conjecture is false.

Important Issues • The halting problem is undecidable. • There’s no black box reasoning engine for standard logic. • Would quantum computing change the picture? • Does undecidability doom our attempt to make artificial copies of ourselves?

Is Decidability Enough?
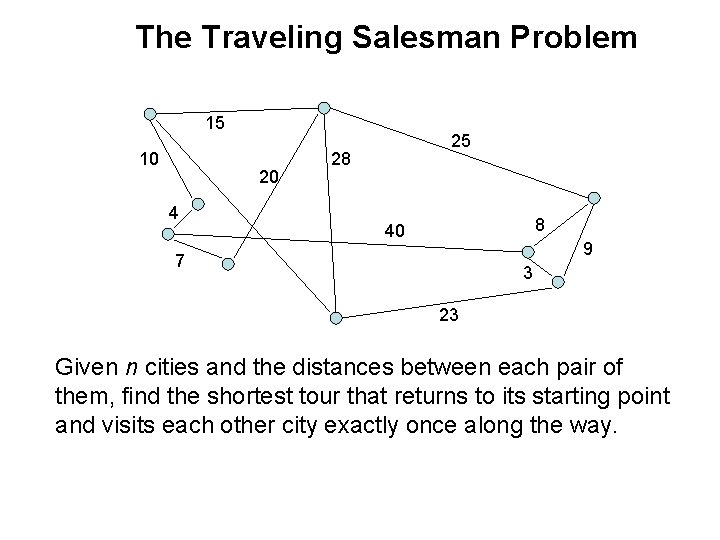
The Traveling Salesman Problem 15 10 20 4 25 28 8 40 9 7 3 23 Given n cities and the distances between each pair of them, find the shortest tour that returns to its starting point and visits each other city exactly once along the way.
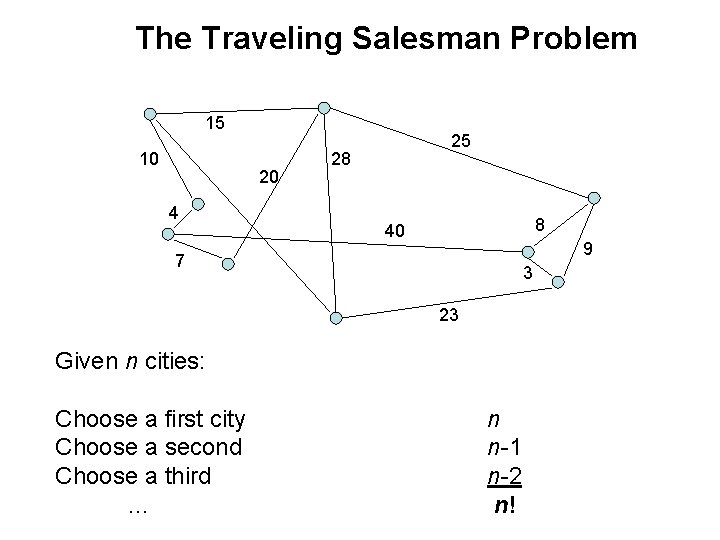
The Traveling Salesman Problem 15 10 20 4 25 28 8 40 9 7 3 23 Given n cities: Choose a first city Choose a second Choose a third … n n-1 n-2 n!

The Traveling Salesman Problem Can we do better than n! ● First city doesn’t matter. ● Order doesn’t matter. So we get (n-1!)/2.

The Growth Rate of n! 2 2 11 479001600 3 6 12 6227020800 4 24 13 87178291200 5 120 14 1307674368000 6 720 15 20922789888000 7 5040 16 355687428096000 8 40320 17 6402373705728000 9 362880 18 121645100408832000 10 3628800 19 2432902008176640000 11 39916800 36 3. 6 1041
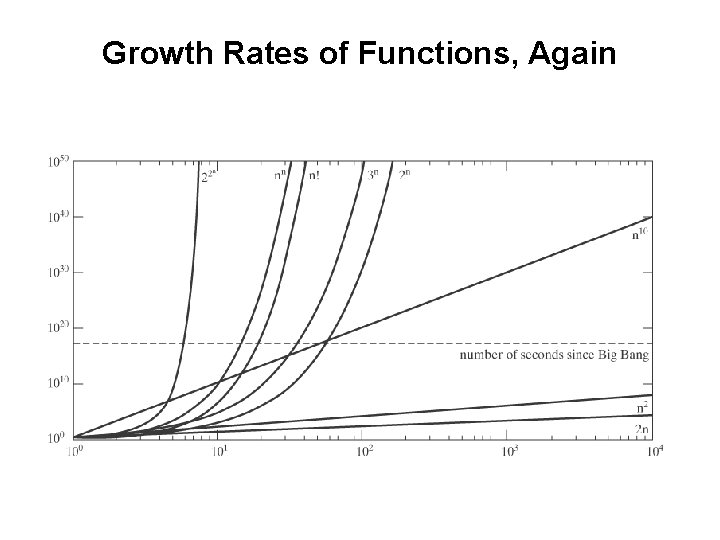
Growth Rates of Functions, Again

Putting it into Perspective Speed of light Width of a proton At one operation in the time it takes light to cross a proton Since Big Bang Ops since Big Bang Neurons in brain Parallel ops since Big Bang 3 108 m/sec 10 -15 m 3 1023 ops/sec 3 1017 sec 9 1040 ops 1011 9 1051 36! = 3. 6 1041 43! = 6 1052

Does Complexity Doom AI?

The Prisoner’s Dilemma

The Prisoner’s Dilemma A cooperates B defects (rats) A: six months B: six months A: 10 years B: goes free A defects (rats) A: goes free B: 10 years A: 5 years B: 5 years

The Prisoner’s Dilemma A cooperates B defects (rats) A: six months A: 10 years A defects (rats) A: goes free A: 5 years

The Theory of Games • Zero-sum games • Nonzero-sum games • Prisoner’s Dilemma

The Theory of Games • Zero-sum games • Chess • The fight for page rank • Nonzero-sum games • Prisoner’s Dilemma

The Prisoner’s Dilemma • Defect dominates cooperate. • A single Nash equilibrium (defect/defect) • (No one can unilaterally improve his position) B cooperates B defects (rats) A cooperates A: six months B: six months A: 10 years B: goes free A defects (rats) A: goes free B: 10 years A: 5 years B: 5 years

The Prisoner’s Dilemma • Defect dominates cooperate. • A single Nash equilibrium (defect/defect) • (No one can unilaterally improve his position) • A single Pareto optimum • (There exists no alternative that is better for at least one player and not worse for anyone. ) B cooperates B defects (rats) A cooperates A: six months B: six months A: 10 years B: goes free A defects (rats) A: goes free B: 10 years A: 5 years B: 5 years

The Prisoner’s Dilemma • Defect dominates cooperate. • A single Nash equilibrium (defect/defect) • (No one can unilaterally improve his position) B cooperates B defects (rats) A cooperates A: six months B: six months A: 10 years B: goes free A defects (rats) A: goes free B: 10 years A: 5 years B: 5 years • A single Pareto optimum • (There exists no alternative that is better for at least one player and not worse for The Nash equilibrium is not Pareto optimal. anyone. )
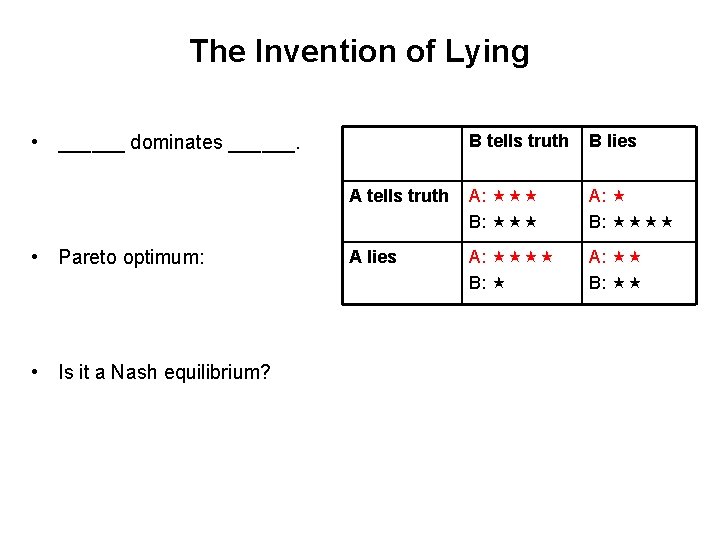
The Invention of Lying • ______ dominates ______. • Pareto optimum: • Is it a Nash equilibrium? B tells truth B lies A tells truth A: B: A: B: A lies A: B: A: B:
Landis, Admitting Doping, Accuses Top U. S. Cyclists Floyd Landis, left, accused his former teammates, including Lance Armstrong, riding in the 2004 Tour de France, of doping. http: //www. nytimes. com/2010/05/21/sports/cycling/21 landis. html? emc=eta 1
- Slides: 119