Computao Grfica TCC00291 Assunto Rasterizao 2 Rasterizao Introduo

Computação Gráfica TCC-00291 Assunto: Rasterização

2 Rasterização Introdução Representação Vetorial x Matricial os da cena através de primitivas geométricas: pontos, segmentos de reta

3 Rasterização Introdução Representação Vetorial x Matricial os da cena através de primitivas geométricas: pontos, segmentos de reta Representação vetorial

4 Rasterização Introdução Representação Vetorial x Matricial Dispositivos gráficos podem ser pensados como matrizes de pixels.

5 Rasterização Introdução Representação Vetorial x Matricial Dispositivos gráficos podem ser pensados como matrizes de pixels. Representação matricial

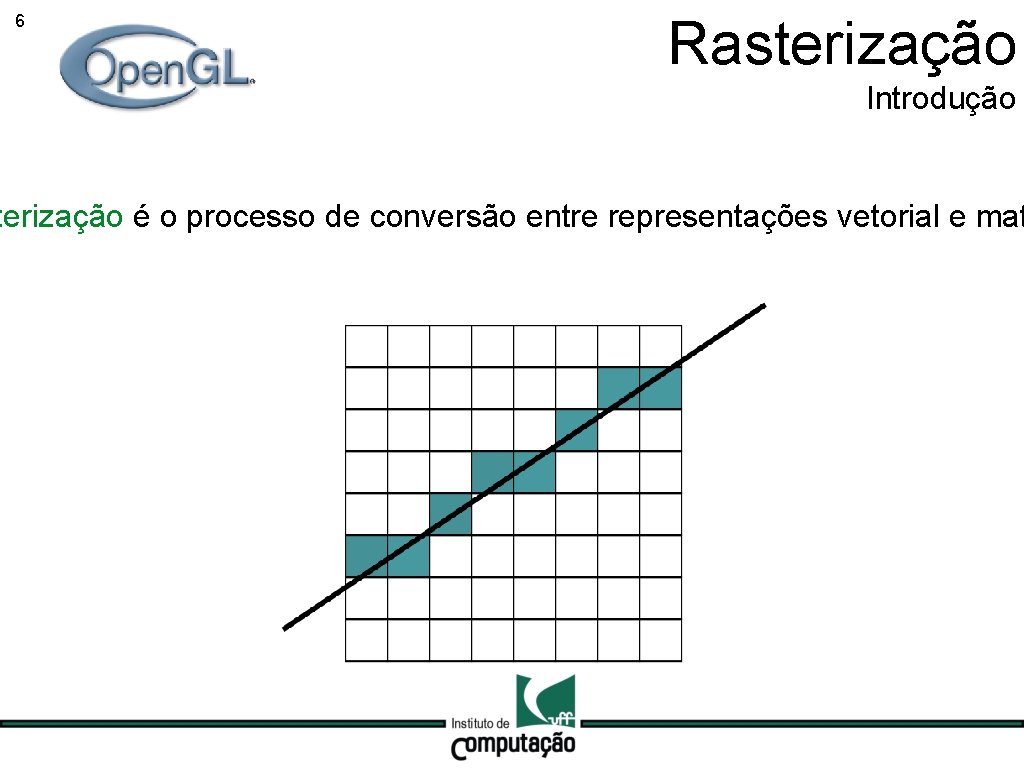
6 Rasterização Introdução terização é o processo de conversão entre representações vetorial e mat

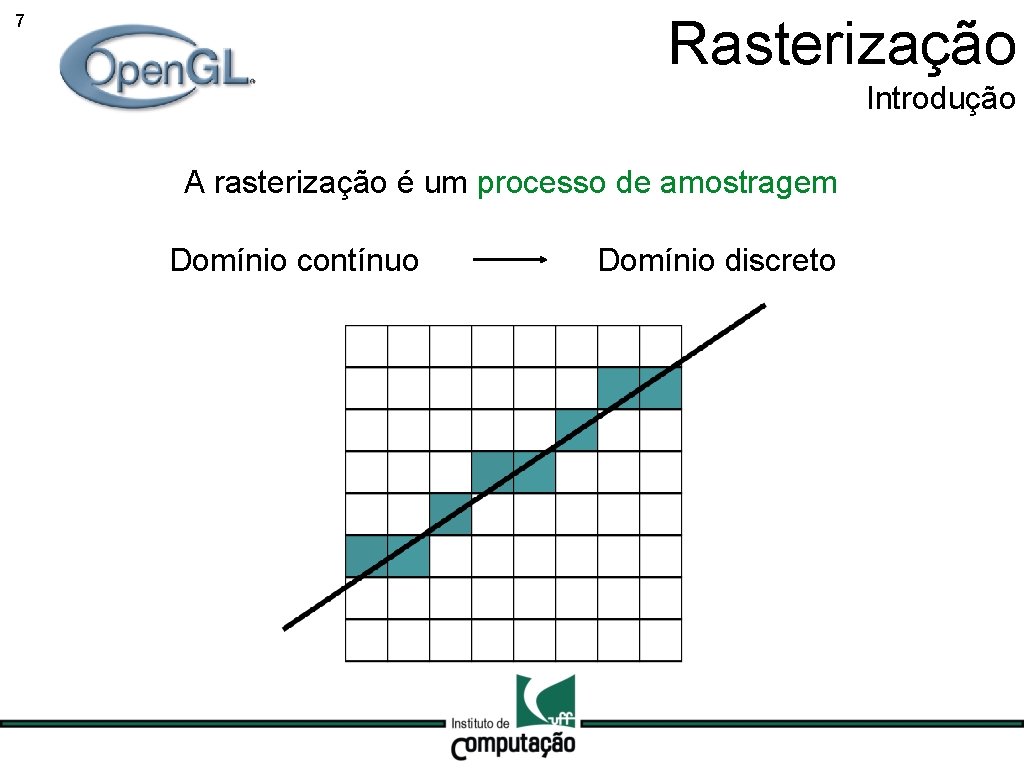
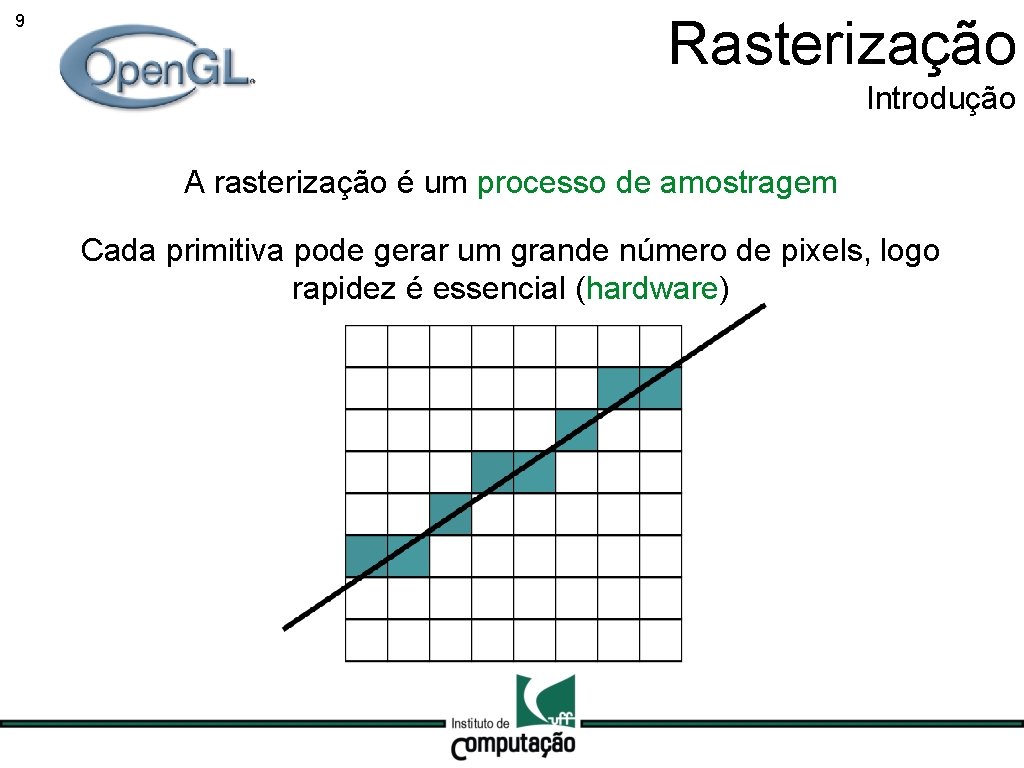
Rasterização 7 Introdução A rasterização é um processo de amostragem Domínio contínuo Domínio discreto

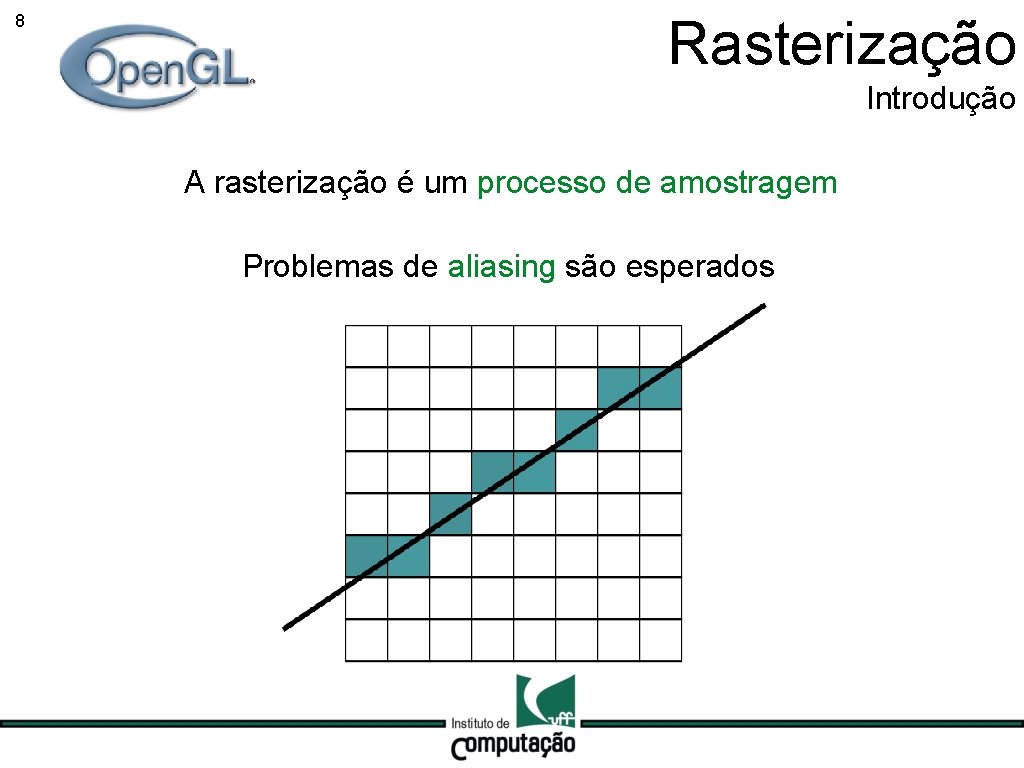
8 Rasterização Introdução A rasterização é um processo de amostragem Problemas de aliasing são esperados

9 Rasterização Introdução A rasterização é um processo de amostragem Cada primitiva pode gerar um grande número de pixels, logo rapidez é essencial (hardware)

10 Rasterização Introdução Estudaremos apenas a rasterização de segmentos de reta e de polígonos.

11 Rasterização Introdução Estudaremos apenas a rasterização de segmentos de reta e de polígonos. Assumiremos que as primitivas já foram clippadas estão contidas no volume de visão.

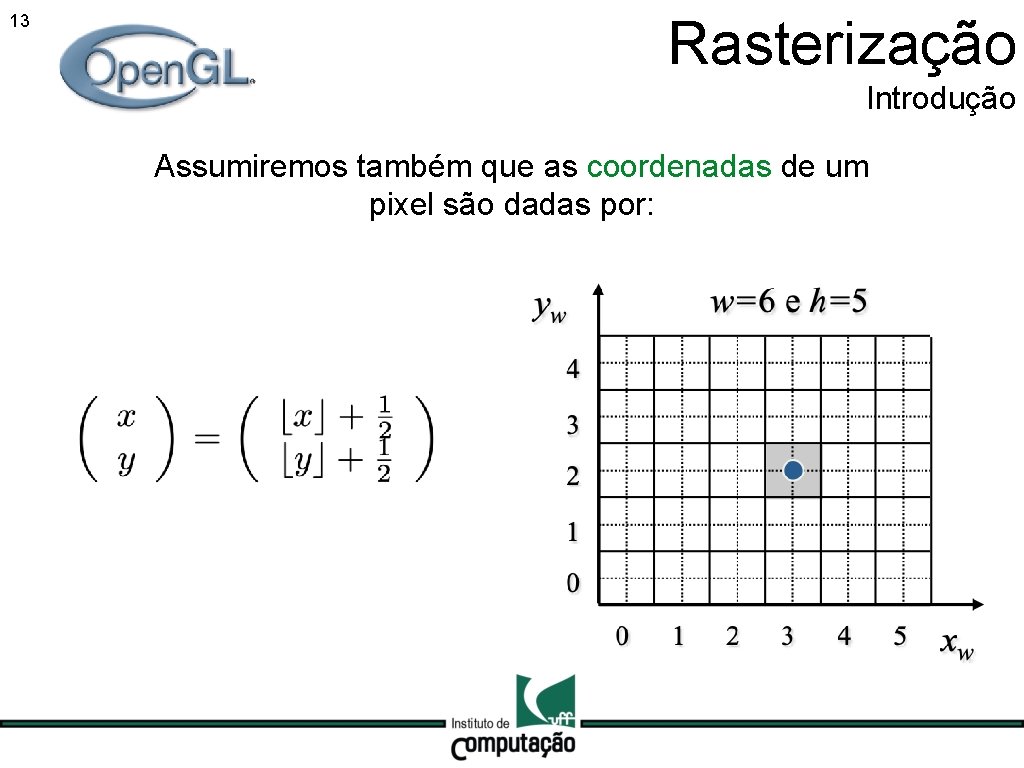
12 Rasterização Introdução Estudaremos apenas a rasterização de segmentos de reta e de polígonos. Assumiremos que as primitivas já foram clippadas estão contidas no volume de visão. Assumiremos também que as coordenadas de um pixel são dadas por:

13 Rasterização Introdução Assumiremos também que as coordenadas de um pixel são dadas por:

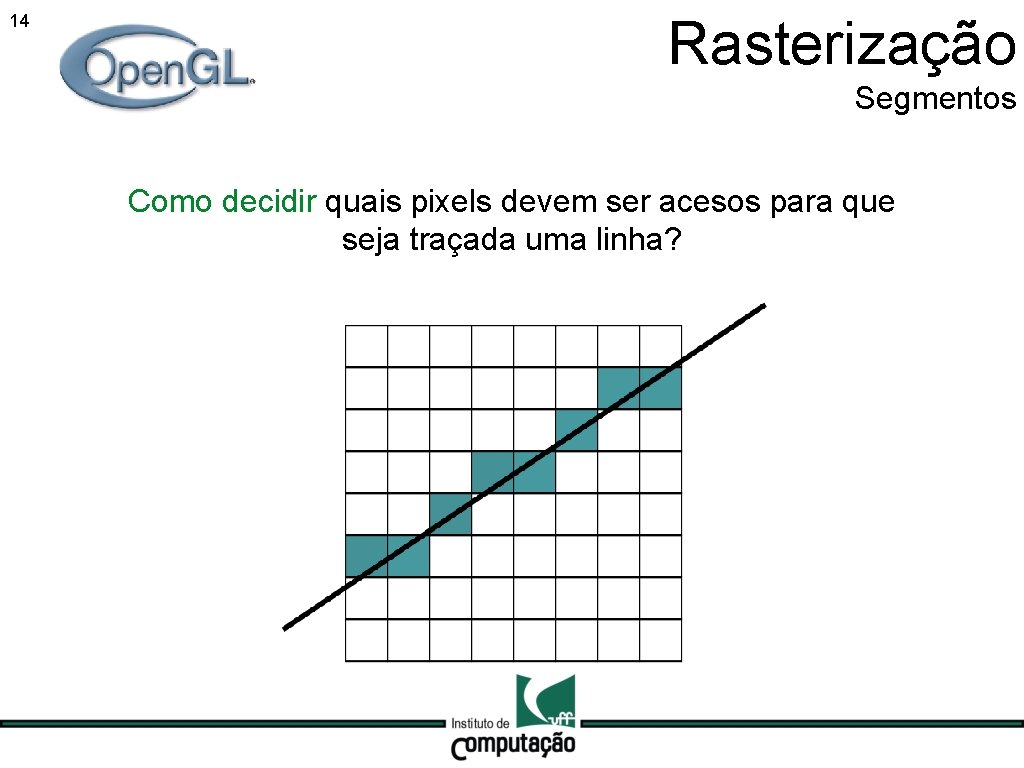
14 Rasterização Segmentos Como decidir quais pixels devem ser acesos para que seja traçada uma linha?

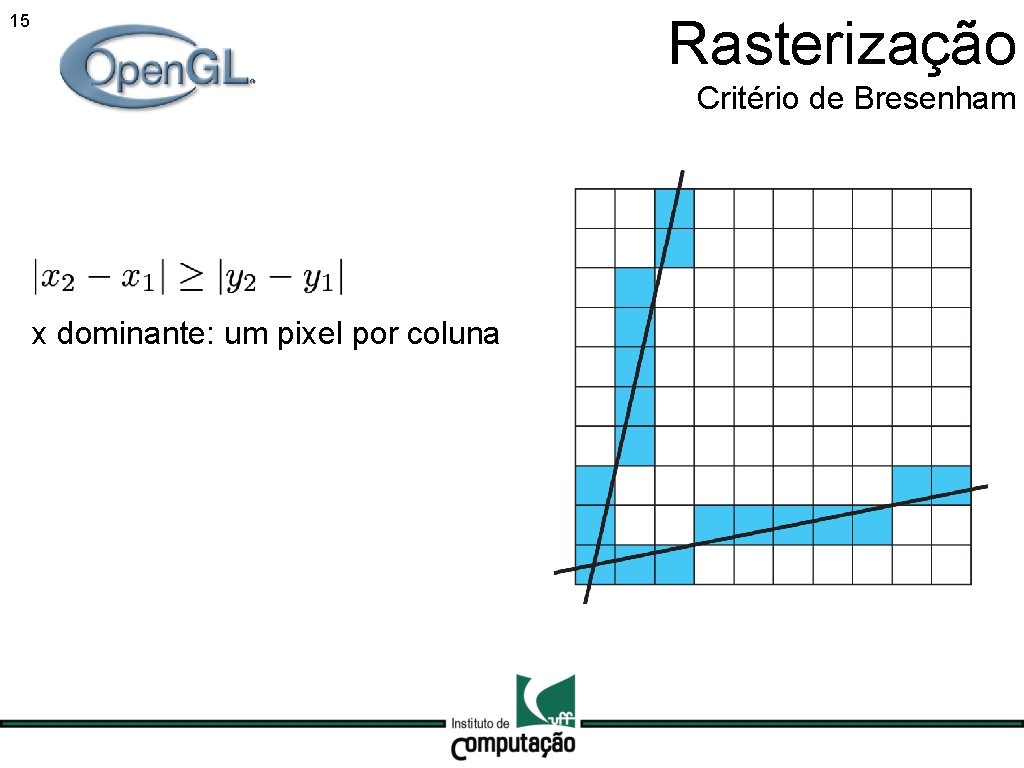
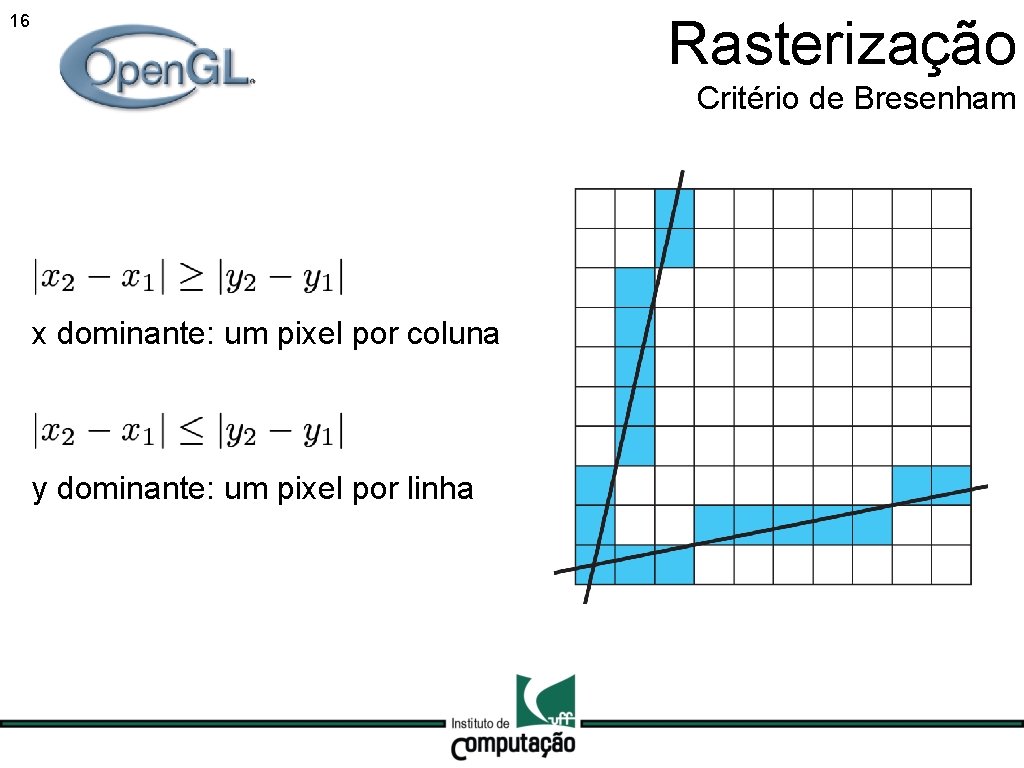
Rasterização 15 Critério de Bresenham x dominante: um pixel por coluna

Rasterização 16 Critério de Bresenham x dominante: um pixel por coluna y dominante: um pixel por linha

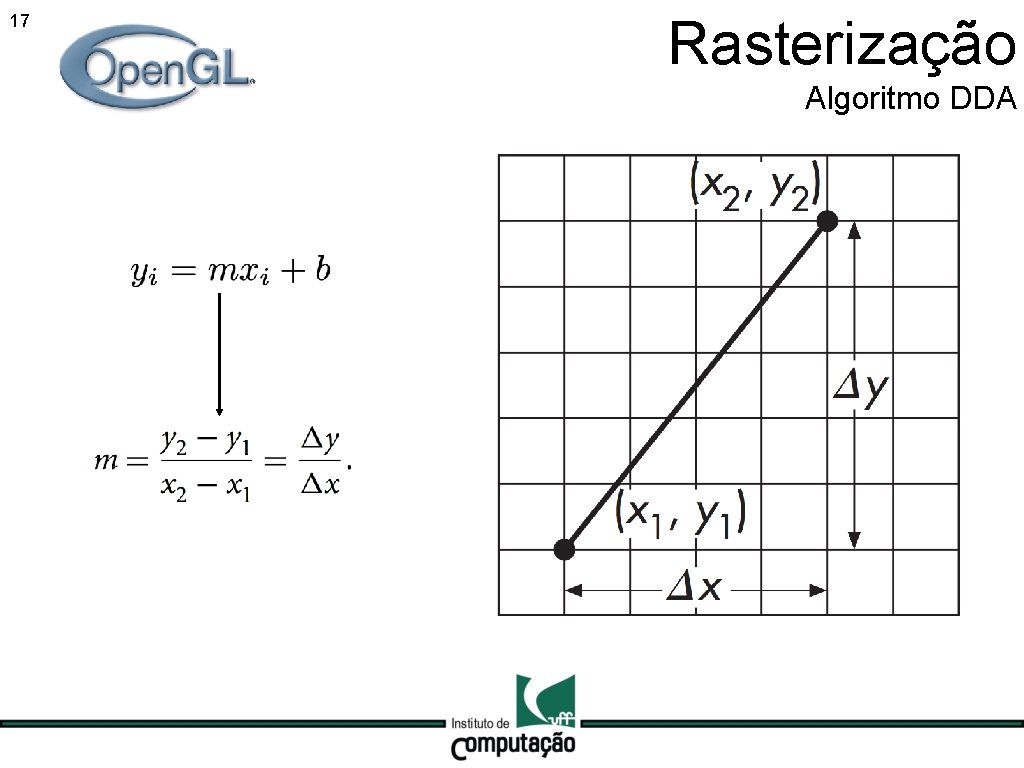
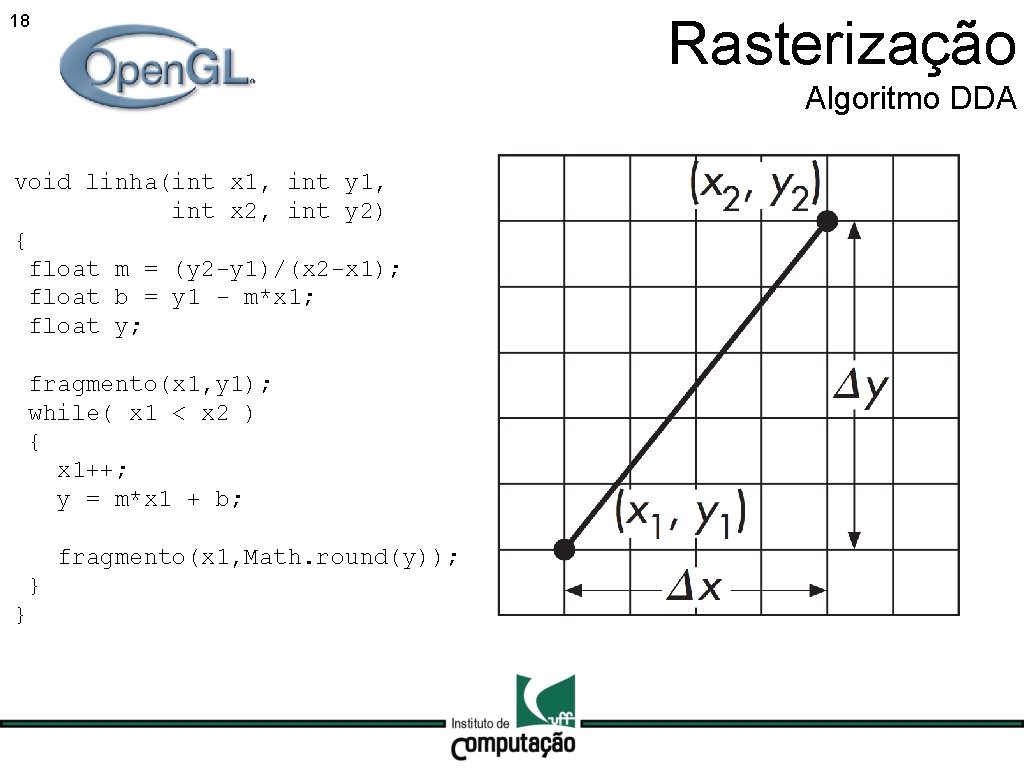
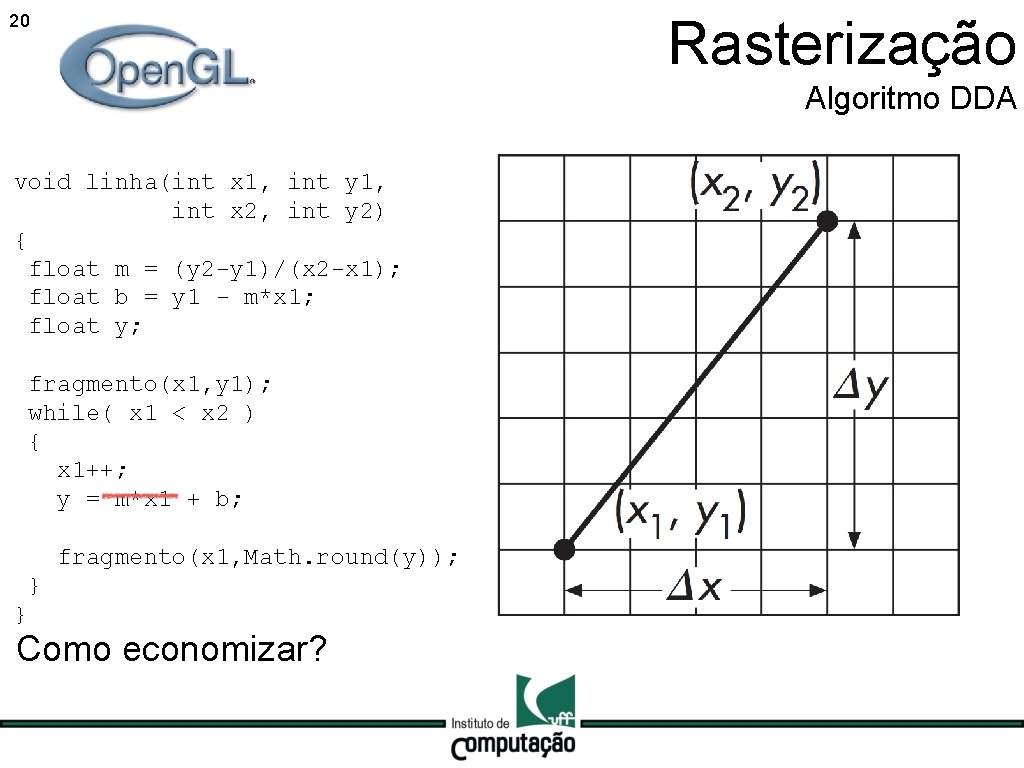
17 Rasterização Algoritmo DDA

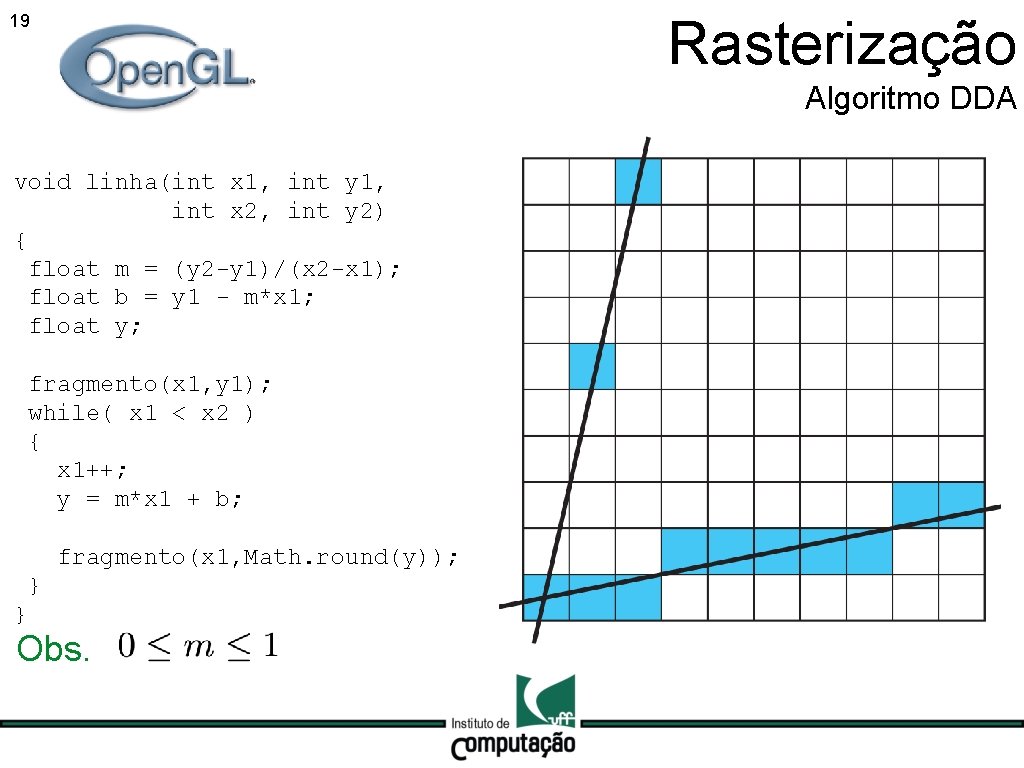
Rasterização 18 Algoritmo DDA void linha(int x 1, int y 1, int x 2, int y 2) { float m = (y 2 -y 1)/(x 2 -x 1); float b = y 1 - m*x 1; float y; fragmento(x 1, y 1); while( x 1 < x 2 ) { x 1++; y = m*x 1 + b; fragmento(x 1, Math. round(y)); } }

Rasterização 19 Algoritmo DDA void linha(int x 1, int y 1, int x 2, int y 2) { float m = (y 2 -y 1)/(x 2 -x 1); float b = y 1 - m*x 1; float y; fragmento(x 1, y 1); while( x 1 < x 2 ) { x 1++; y = m*x 1 + b; fragmento(x 1, Math. round(y)); } } Obs.

Rasterização 20 Algoritmo DDA void linha(int x 1, int y 1, int x 2, int y 2) { float m = (y 2 -y 1)/(x 2 -x 1); float b = y 1 - m*x 1; float y; fragmento(x 1, y 1); while( x 1 < x 2 ) { x 1++; y = m*x 1 + b; fragmento(x 1, Math. round(y)); } } Como economizar?

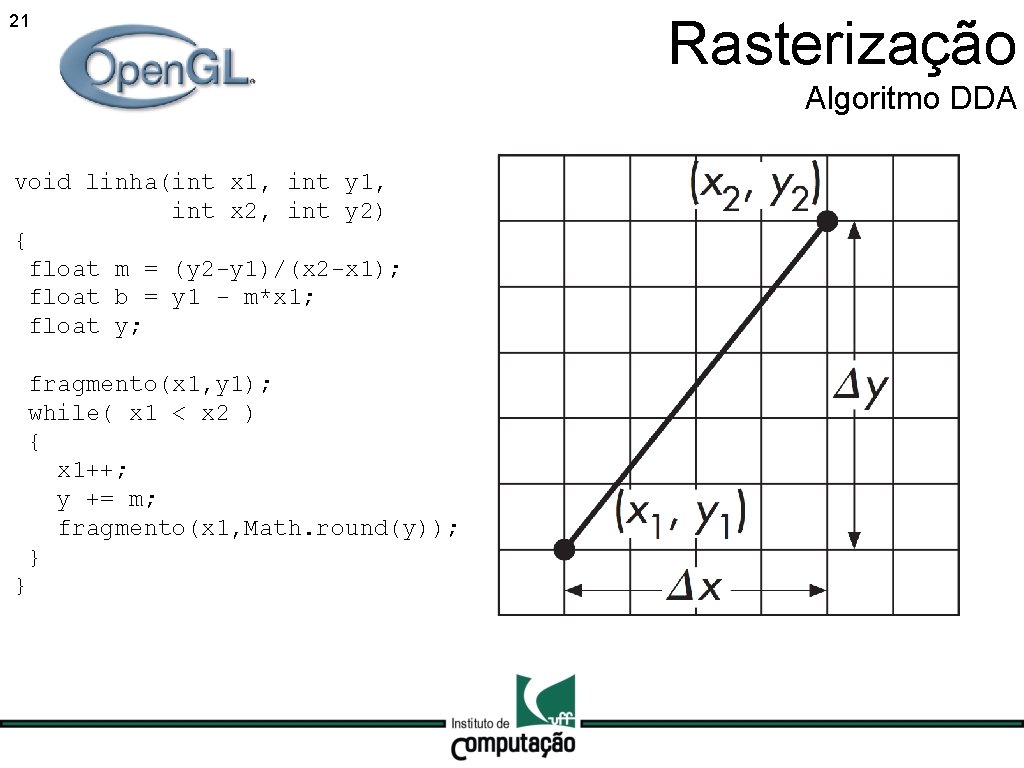
21 Rasterização Algoritmo DDA void linha(int x 1, int y 1, int x 2, int y 2) { float m = (y 2 -y 1)/(x 2 -x 1); float b = y 1 - m*x 1; float y; fragmento(x 1, y 1); while( x 1 < x 2 ) { x 1++; y += m; fragmento(x 1, Math. round(y)); } }

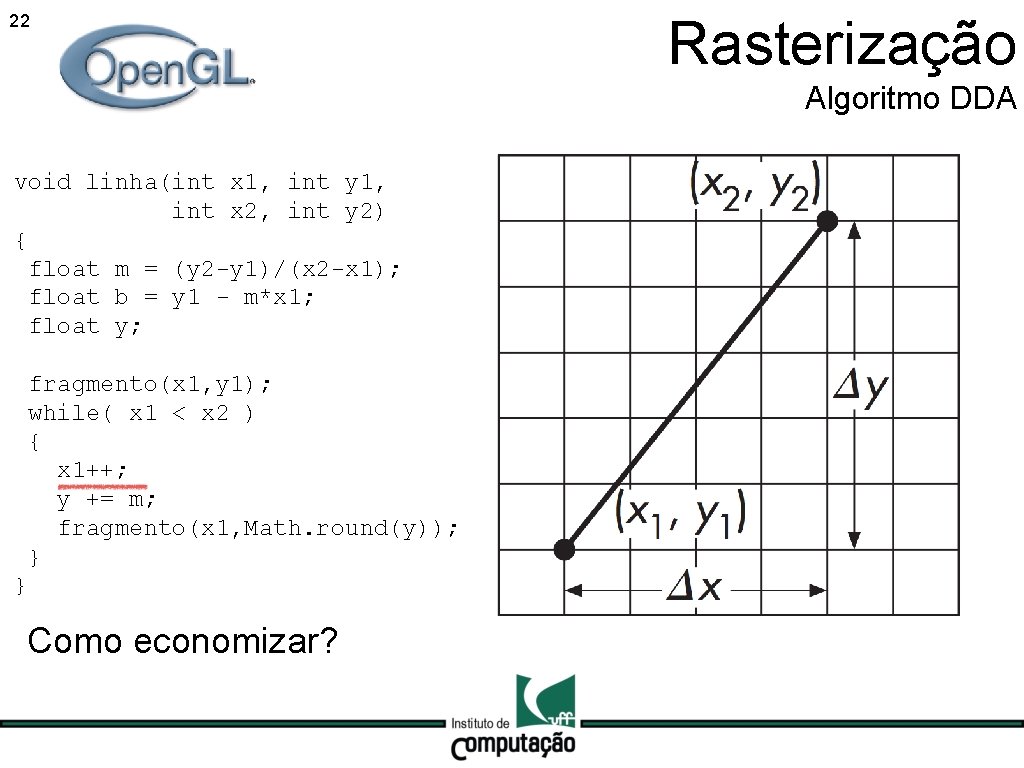
22 Rasterização Algoritmo DDA void linha(int x 1, int y 1, int x 2, int y 2) { float m = (y 2 -y 1)/(x 2 -x 1); float b = y 1 - m*x 1; float y; fragmento(x 1, y 1); while( x 1 < x 2 ) { x 1++; y += m; fragmento(x 1, Math. round(y)); } } Como economizar?

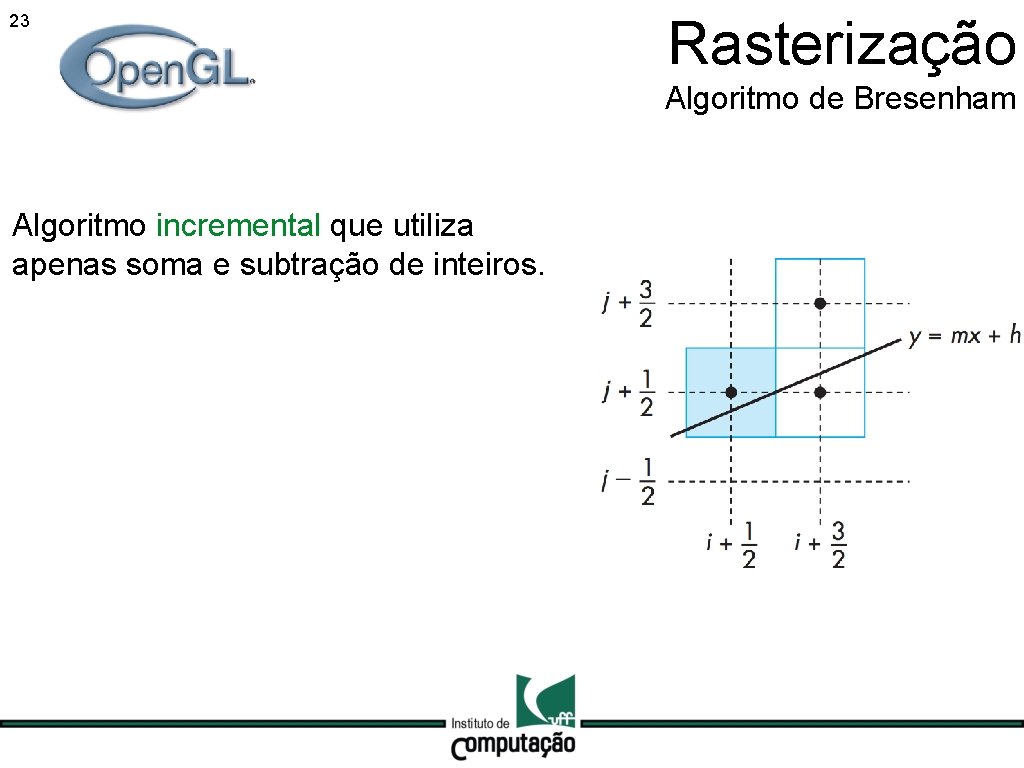
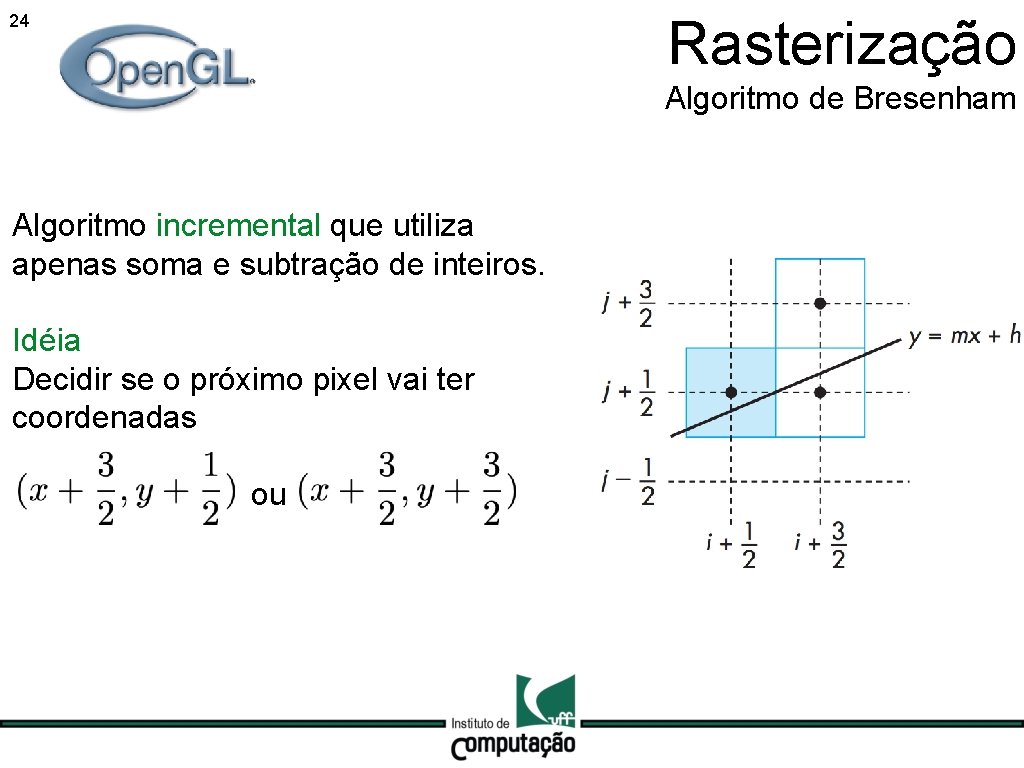
23 Rasterização Algoritmo de Bresenham Algoritmo incremental que utiliza apenas soma e subtração de inteiros.

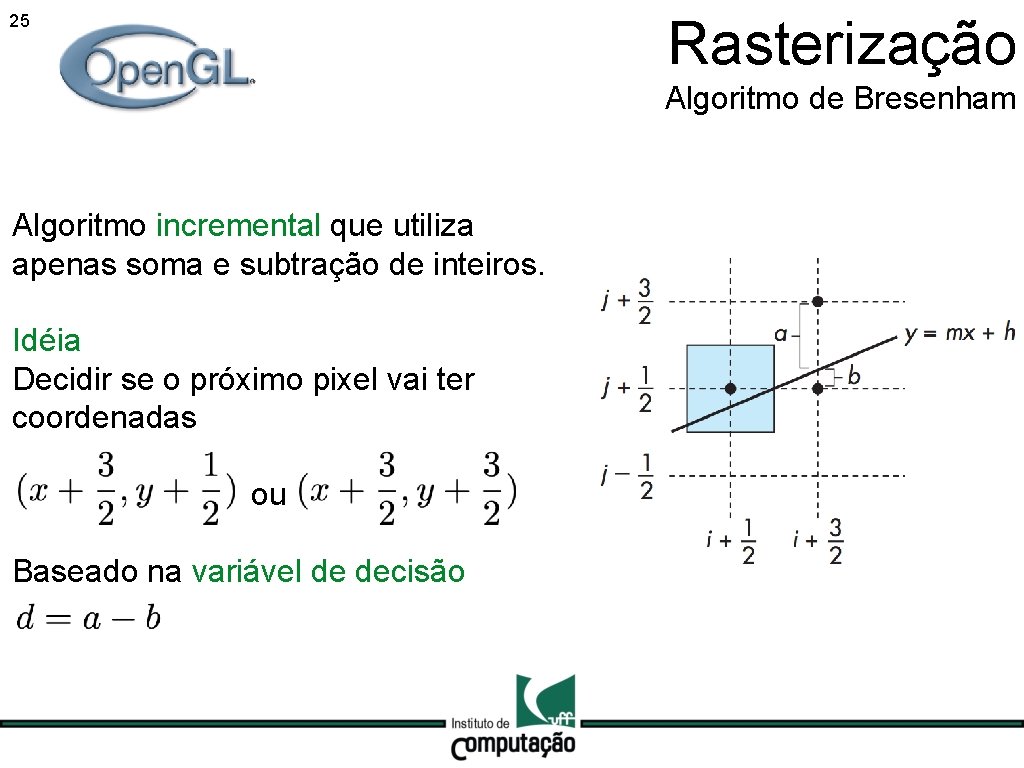
Rasterização 24 Algoritmo de Bresenham Algoritmo incremental que utiliza apenas soma e subtração de inteiros. Idéia Decidir se o próximo pixel vai ter coordenadas ou

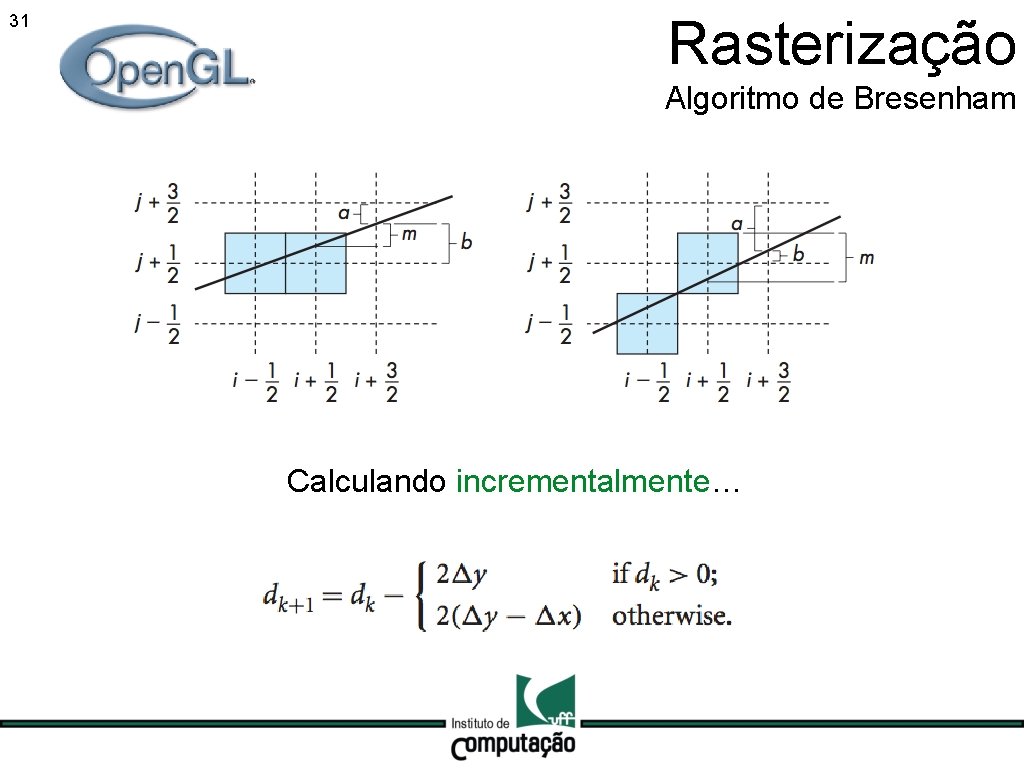
Rasterização 25 Algoritmo de Bresenham Algoritmo incremental que utiliza apenas soma e subtração de inteiros. Idéia Decidir se o próximo pixel vai ter coordenadas ou Baseado na variável de decisão

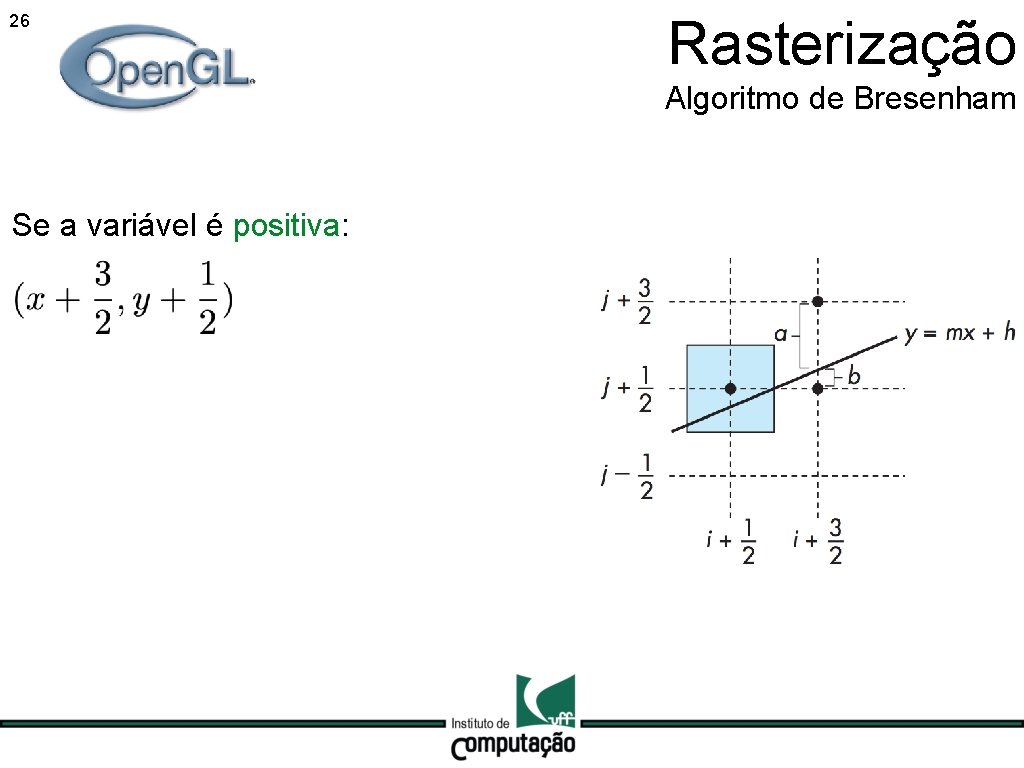
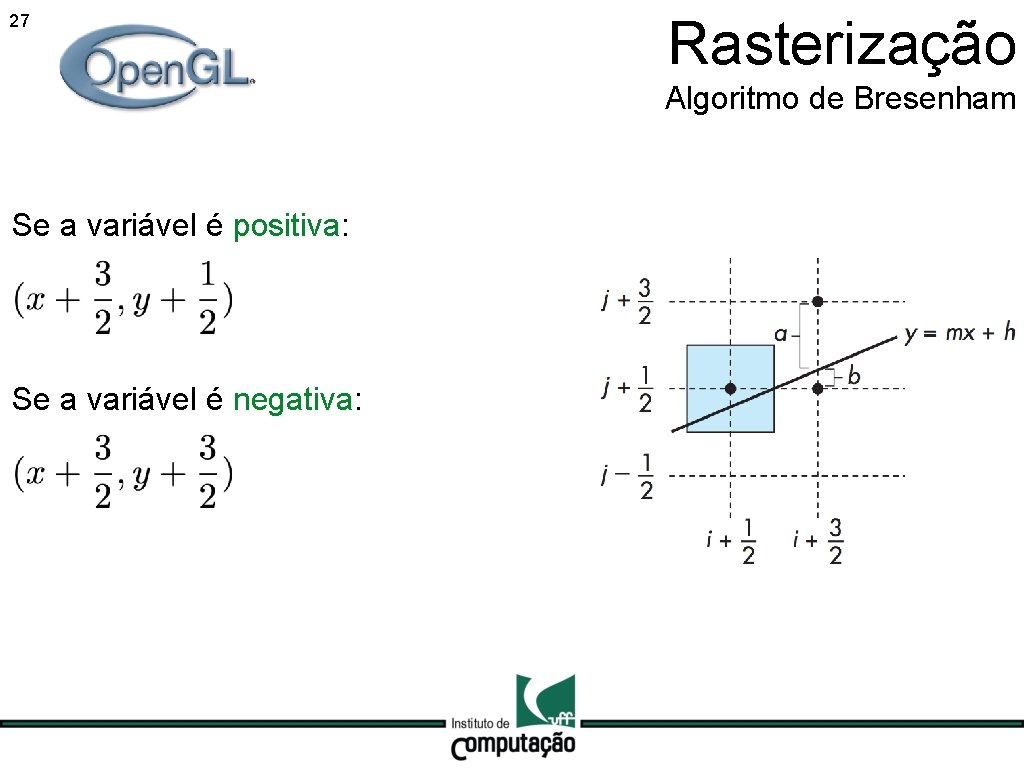
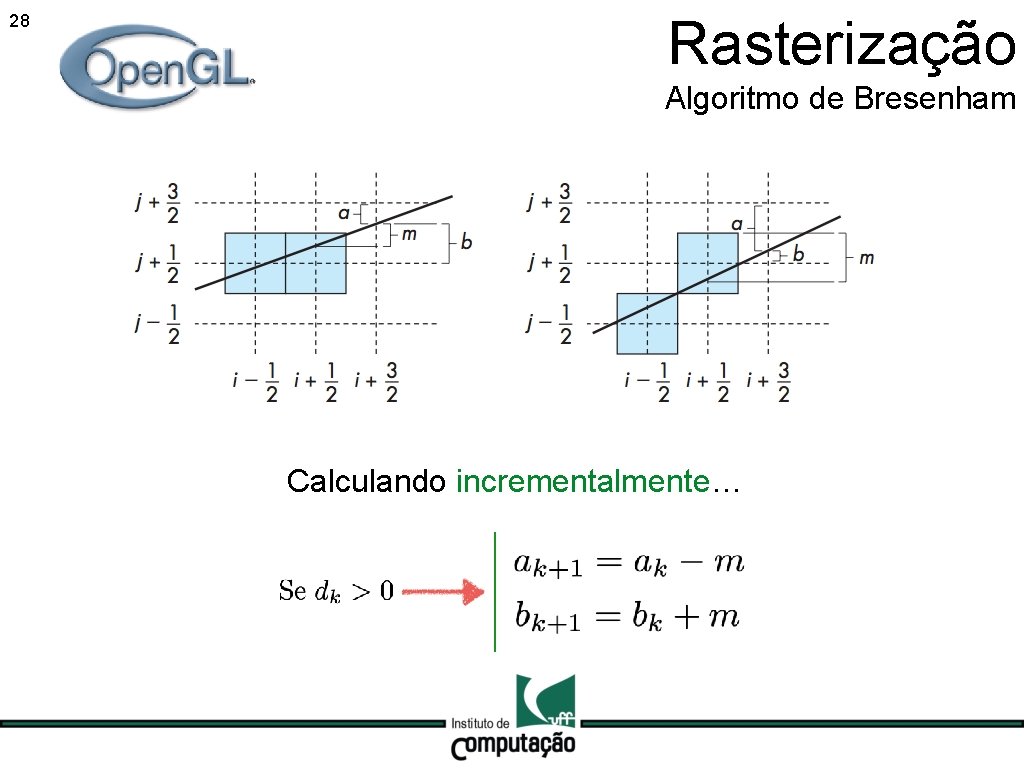
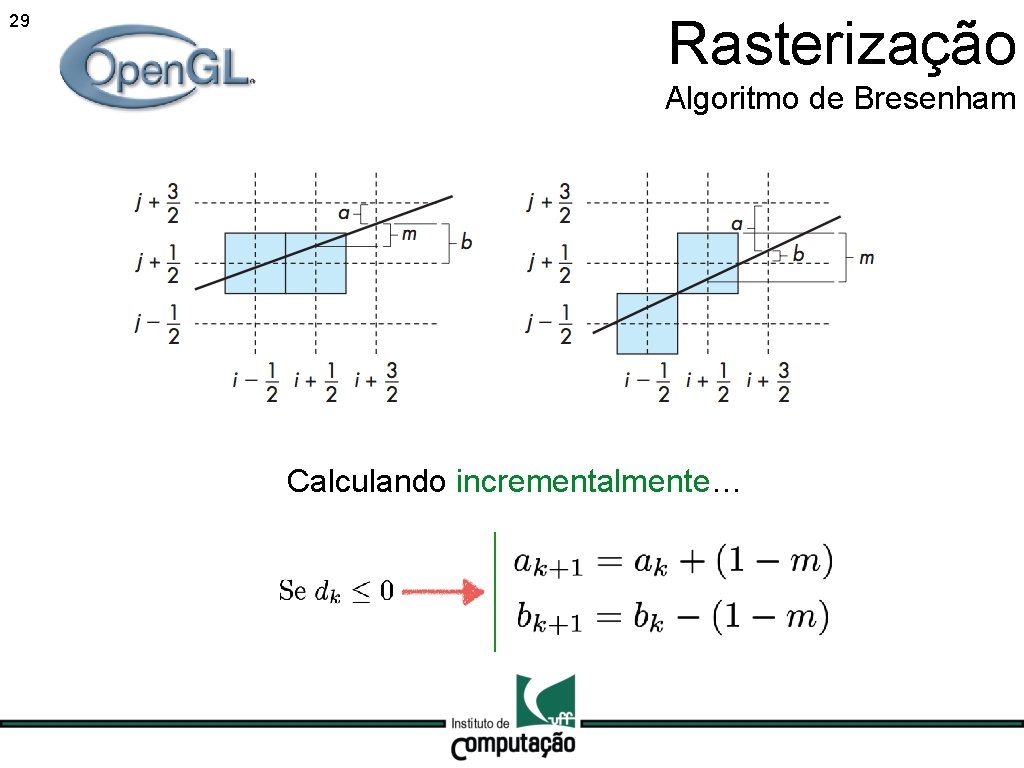
26 Rasterização Algoritmo de Bresenham Se a variável é positiva:

27 Rasterização Algoritmo de Bresenham Se a variável é positiva: Se a variável é negativa:

28 Rasterização Algoritmo de Bresenham Calculando incrementalmente…

29 Rasterização Algoritmo de Bresenham Calculando incrementalmente…

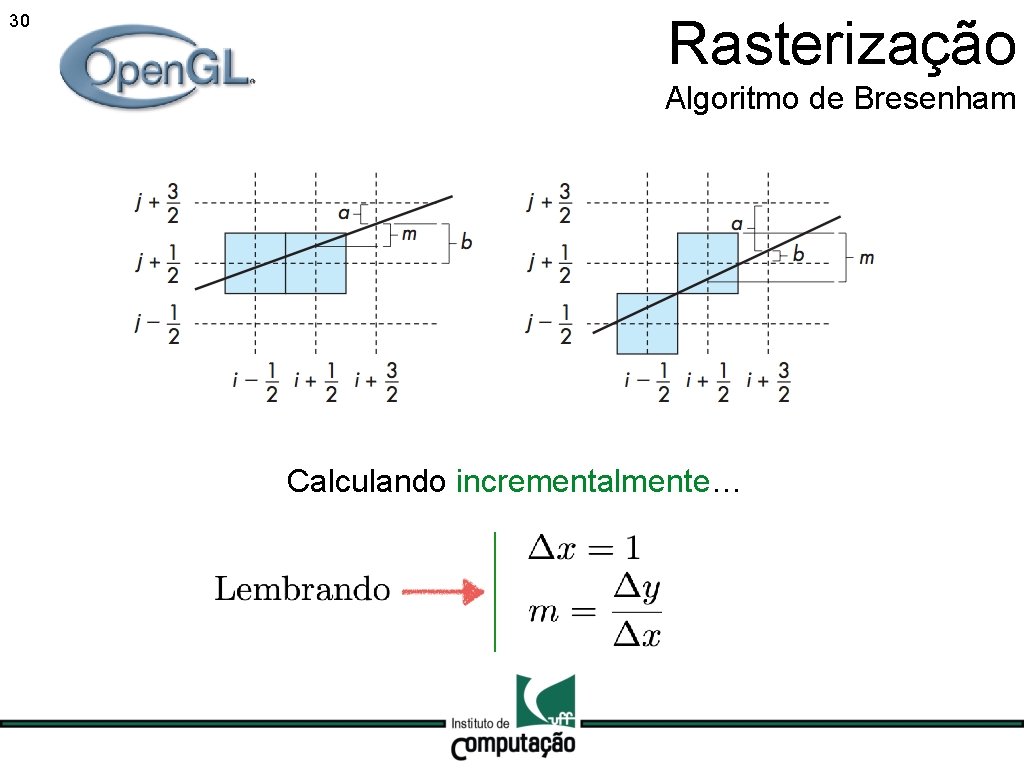
30 Rasterização Algoritmo de Bresenham Calculando incrementalmente…

31 Rasterização Algoritmo de Bresenham Calculando incrementalmente…

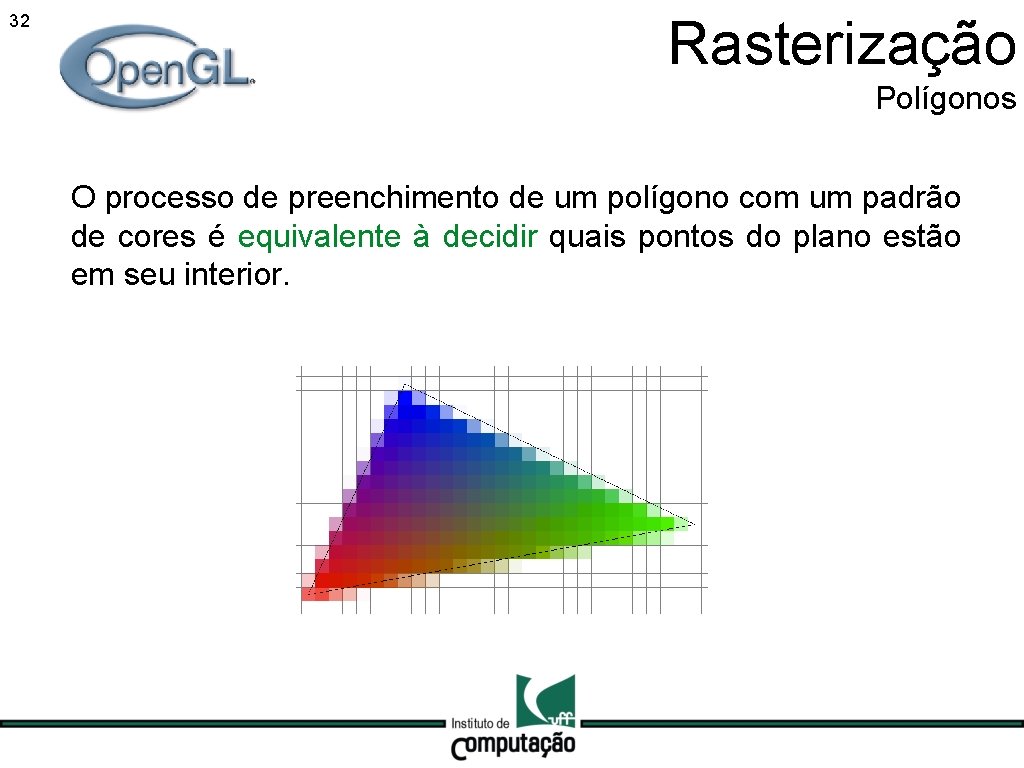
32 Rasterização Polígonos O processo de preenchimento de um polígono com um padrão de cores é equivalente à decidir quais pontos do plano estão em seu interior.

Rasterização 33 Polígonos Teste par ou ímpar. Todo raio saindo de p para o infinito deve cortar um número ímpar de segmentos do polígono, se o ponto for de interior e um número par se o ponto for de exterior.

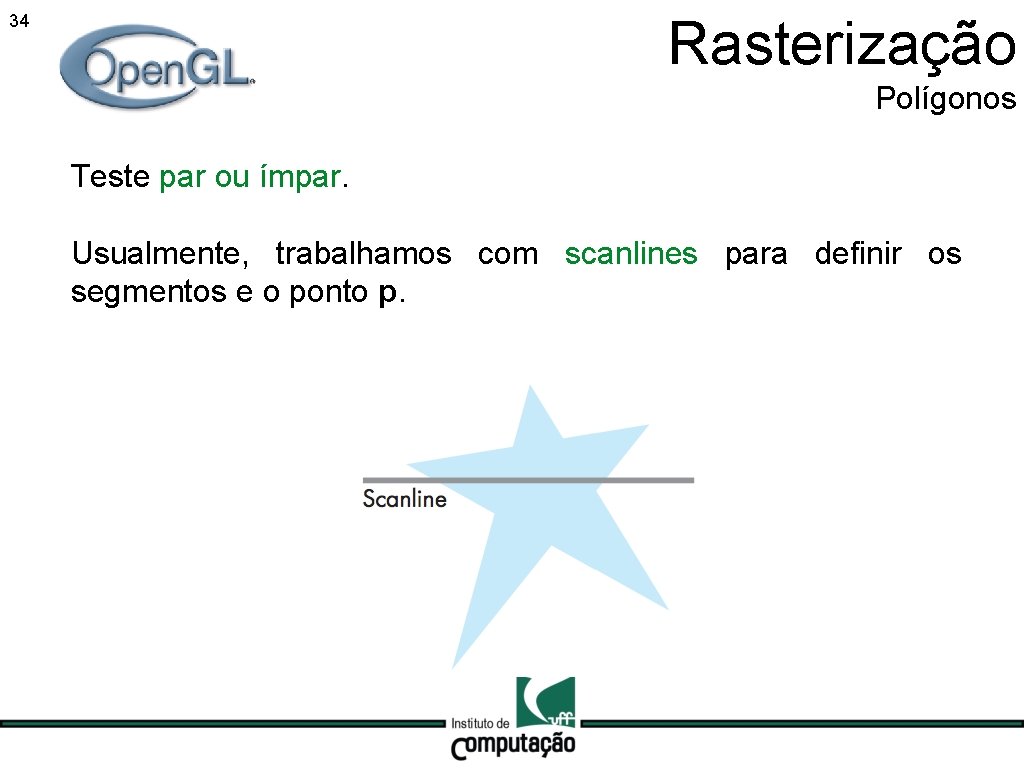
Rasterização 34 Polígonos Teste par ou ímpar. Usualmente, trabalhamos com scanlines para definir os segmentos e o ponto p.

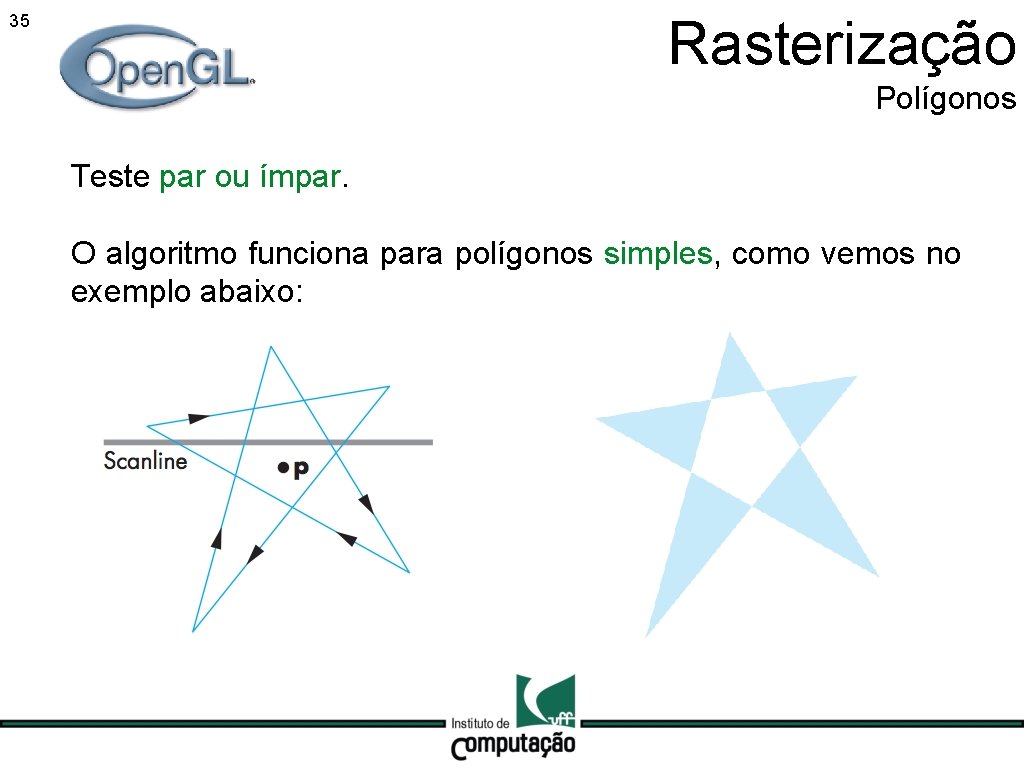
Rasterização 35 Polígonos Teste par ou ímpar. O algoritmo funciona para polígonos simples, como vemos no exemplo abaixo:

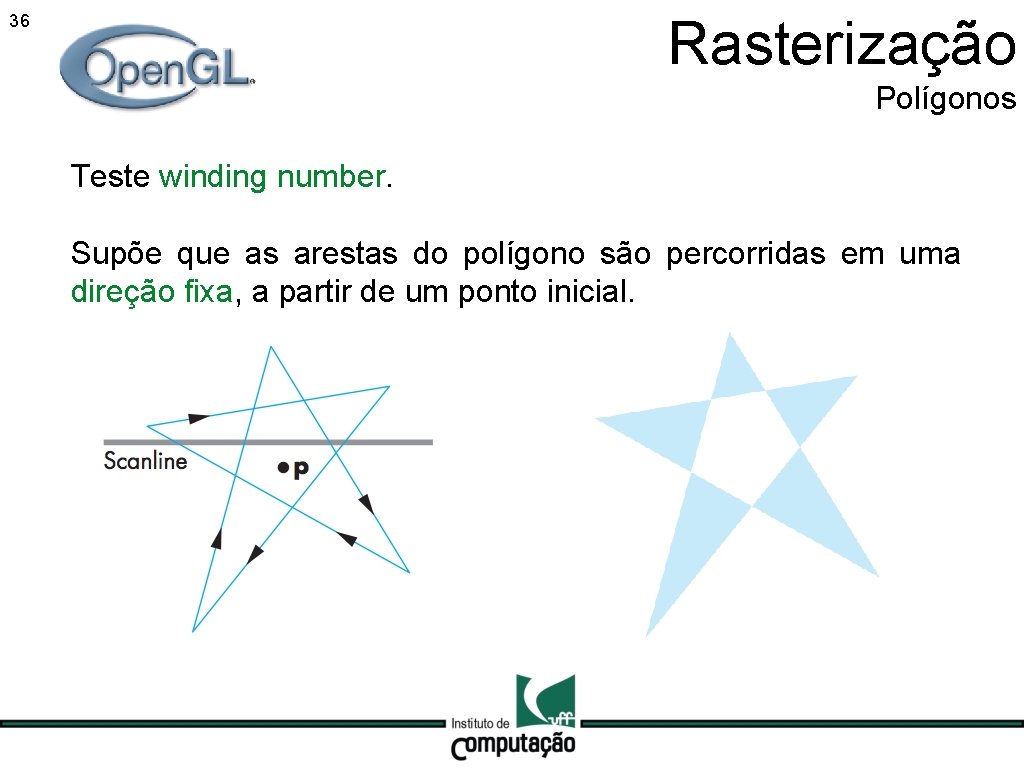
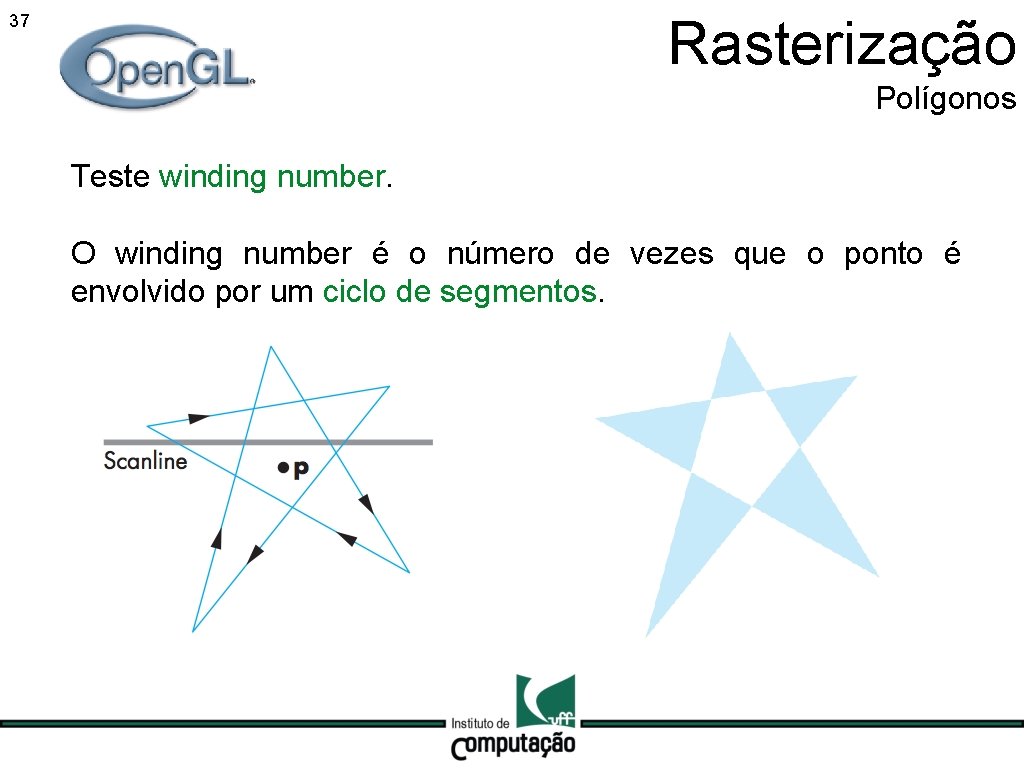
Rasterização 36 Polígonos Teste winding number. Supõe que as arestas do polígono são percorridas em uma direção fixa, a partir de um ponto inicial.

Rasterização 37 Polígonos Teste winding number. O winding number é o número de vezes que o ponto é envolvido por um ciclo de segmentos.

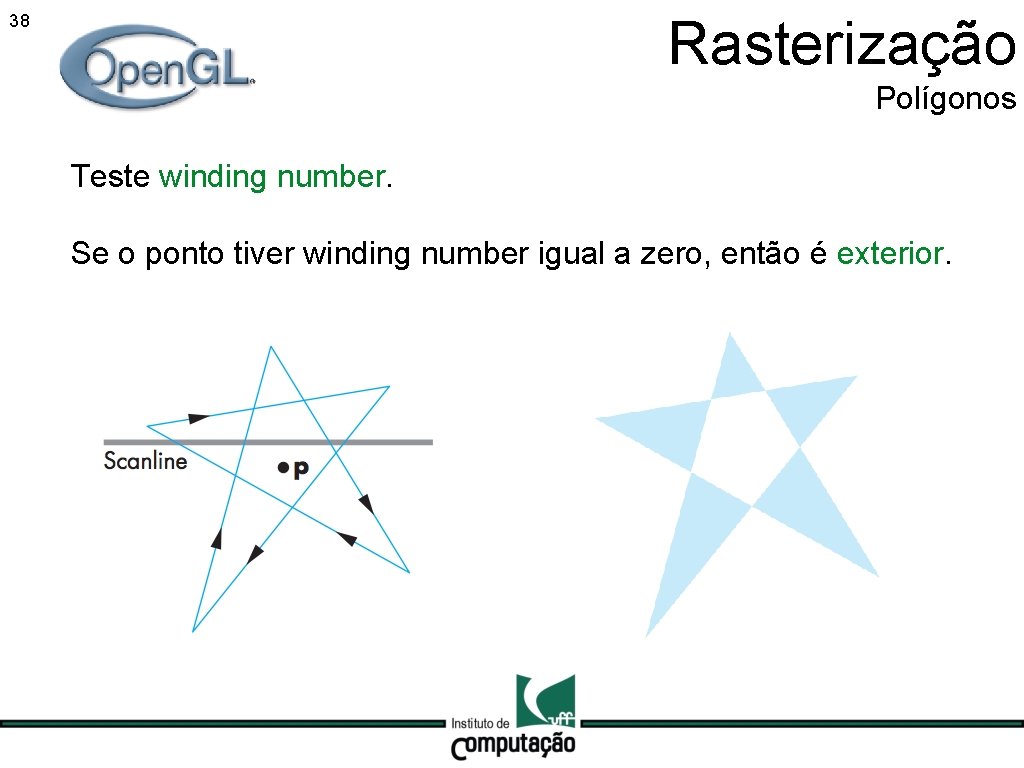
Rasterização 38 Polígonos Teste winding number. Se o ponto tiver winding number igual a zero, então é exterior.

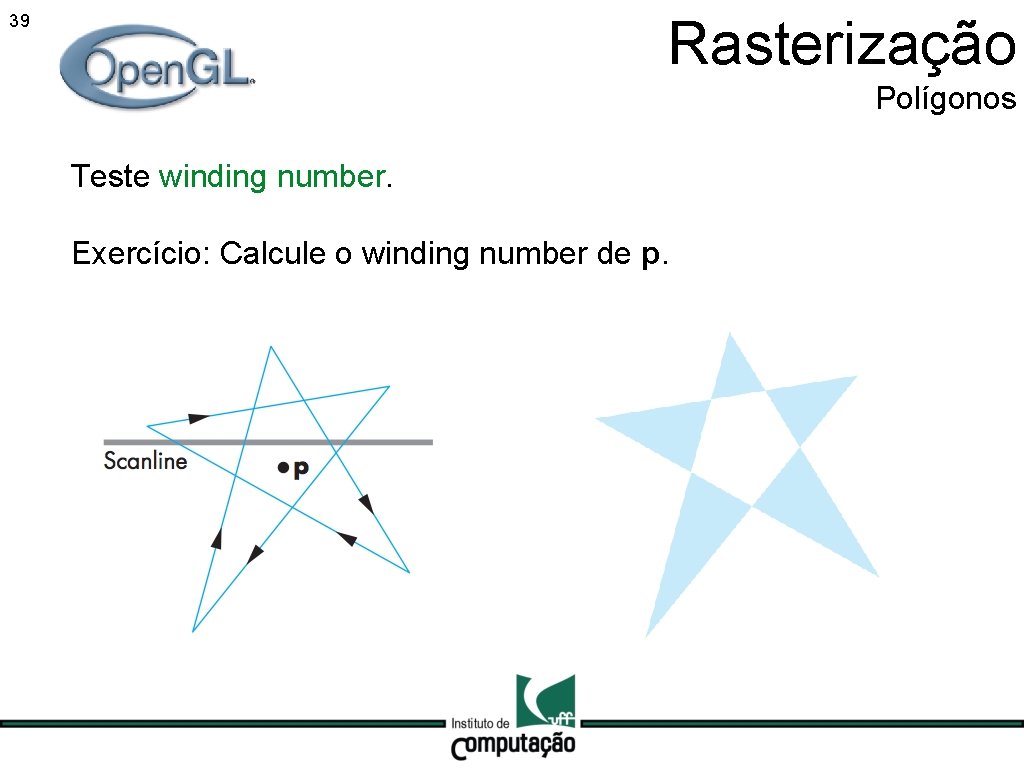
Rasterização 39 Polígonos Teste winding number. Exercício: Calcule o winding number de p.

Computação Gráfica TCC-00291 Assunto: Rasterização