Computao Grfica Modelagem Geomtrica Profa Mercedes Gonzales Mrquez








































- Slides: 51

Computação Gráfica – Modelagem Geométrica Profa. Mercedes Gonzales Márquez

Tópicos l l l Curvas Superfícies Técnicas principais de Modelagem Geométrica

Curvas e Superfícies - Introdução l Curvas são a base, tanto da geração de formas simples, como círculos e elipses, quanto na criação de projetos complexos como automóveis, navios, aeronaves ou até mesmo faces e corpos humanos.

Curvas e Superfícies - Introdução l l Desempenham um papel importante em várias áreas, como criação de objetos e visualização de fenômenos científicos. Uma curva pode ser representada: – – Por uma sucessão de linhas retas que ligam pontos específicos. Por um conjunto de pontos de controle que determina através de uma equação uma curva que passe por eles.

Representação de Curvas l A representação analítica de curvas pode usar ou não parâmetros, sendo classificados como B. 1. paramétricas B. 2. não-paramétricas l As formas não-paramétricas podem ser, ainda, B. 2. 1. explícitas B. 2. 2. implícitas.

Representação de Curvas B. 1 Formas paramétricas As coordenadas são dadas em termos de um (conjunto) de parâmetros. Usa-se um parâmetro (t, , etc. ) para definir as coordenadas dos pontos da curva. P(t) = (x(t), y(t)) Exemplos: –

Representação de Curvas B. 1 Formas paramétricas P(t) = (x(t), y(t)) Exemplos: (1)

Representação de Curvas B. 1. Formas paramétricas P(t) = (x(t), y(t)) Exemplos: (2)

Representação de Curvas B. 2. Formas não-paramétricas Não há parâmetros e uma coordenada da curva é dada em função da outra, ou seja y = f(x) ou x = f(y) –Exemplos: 1) Equação de um semi-círculo de raio 2 2) Equação de uma reta y = 2 x – 1 ou x = ½ (y + 1)

Representação de Curvas B. 2. 1 Forma não-paramétrica explícita : É dada por uma equação do tipo y = f(x), ou seja uma das coordenadas é explicitamente dada em função das outras. Exemplos: 1) Equação genérica explícita de uma parábola: y = ax 2 + bx + c 2) Equação de uma reta y = mx + b 3) Polinômios: P(x) = anxn + an-1 xn-1 +. . . + a 2 x 2 + a 1 x 1 + a 0

Representação de Curvas l Obtém-se um valor de y para cada valor de x dado.

Representação de Curvas l B. 2. 2. A Forma não-paramétrica implícita não tem essa limitação. Nela as coordenadas são relacionadas por uma função. A sua forma é f(x, y)=0 ou f(x, y, z)=0. l Exemplo: x 2 + y 2 = R 2, f(x, y)= x 2 + y 2 - R 2= 0

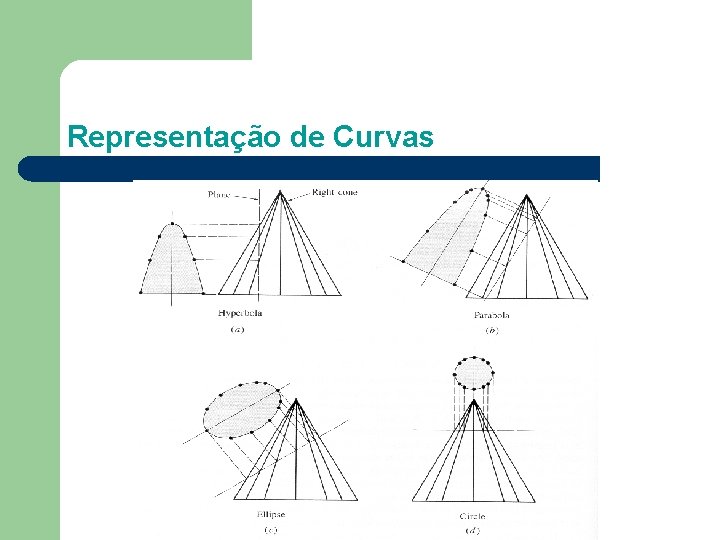
Representação de Curvas l l Exemplo: seções cônicas. ax 2 + bxy + cy 2 + dx + ey + f = 0 Essa expressão representa a variedade de curvas planas denominadas seções cônicas. Essas curvas (cinco) são obtidas pelo corte de um cone por um plano, resultando em: círculo, elipse, parábola, hipérbole, reta.

Representação de Curvas

Representação de Curvas Cônica Forma Paramétrica Elipse x = a cos y = b sen Parábola x = at 2, y = 2 at Hipérbole x = a cosh y = b senh Forma Implícita y 2 – 4 ax = 0

Exercício Veja programas circle. cpp, parabola. cpp, helix. cpp

Curvas de Bézier l l É uma técnica de aproximação de curvas. Uma curva de Bézier pode ser gerada por 3, 4, até n + 1 pontos de controle (ajuste para um polinômio de grau n). Geralmente utiliza-se quatro pontos de controle (forma cúbica). A curva passa pelo primeiro e pelo último ponto de controle.

Curvas de Bézier B 2 B 1 B 3 B 0 Figura 1

Curvas de Bézier l A curva paramétrica de Bézier é definida como: l. Onde Bi representa cada um dos n+1 pontos de controle considerados e Jn, i (t) são as funções que combinam a influência de todos os pontos (blending functions). l. Essas funções são descritas pelos polinômios de Bernstein como:

Curvas de Bézier onde n é o grau dos polinômios e: l (i = 0, 1, . . . , n) são os coeficientes binomiais. l Essas funções Jn, i (t) devem satisfazer as condições: Jn, i (t) 0 para todo i entre 0 e 1, isto é 0 ≤ t ≤ 1 e também:

Curvas de Bézier l Expressões que definem as curvas de Bézier: – Para três pontos de controle polinômios com grau 2. P(t) = (1 – t)2 B 0 + 2 t (1 – t) B 1 + t 2 B 2, onde t inicialmente é 0.

Curvas de Bézier l Expressões que definem as curvas de Bézier: – Para quatro pontos de controle polinômios com grau 3. P(t) = (1 – t)3 B 0 + 3 t (1 – t)2 B 1 + 3 t 2 (1 – t)B 2 + t 3 B 3, onde t inicialmente é 0.

Curvas de Bézier - Algoritmo § § Exercício: (1) Leia e entenda os programas bezier. Curves. cpp e bezier. Curve. With. Eval. Mesh. cpp que desenham curvas de Bézier usando comandos de Open. GL. Consulte e explique os comandos que geram as curvas em ambos programas. (2) O programa superficies. cpp permite o ingresso interativo (pelo cliques do mouse) de n+1 pontos de controle e constrói a curva de Bézier correspondente. O programa funciona, mas pode ser melhorado. Faça isso.

Curvas de Bézier - Problemas 1. Falta de controle local : Uma alteração em um ponto no polígono de Bézier acarreta alterações em toda a curva de Bézier. Indesejável quando desejamos fazer ajustes finos. 2. de controle do polígono de controle.

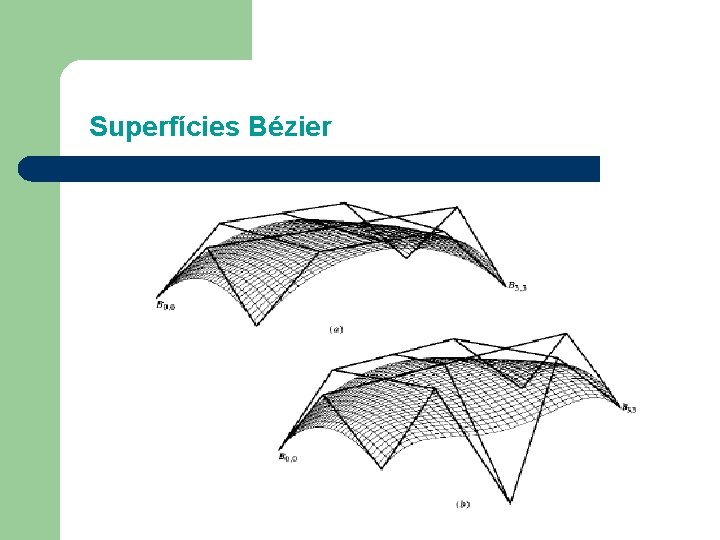
Superfícies Bézier - Generalização da idéia de curva de Bézier. - Sejam Bij, i=0, . . . , m, j=0, . . . , n, um conjunto de pontos no R 3 de tal forma que sua projeção no plano x 0 y seja formada pelos vértices de mn retângulos de mesmas dimensões. A superfície de Bézier definida no domínio [0, 1]x[0, 1] é Onde Jni e Kmj são os polinômios de Bernstein.

Superfícies Bézier

Curvas e Superfícies Bézier em Open. GL 1. Leia e entenda os programas bezier. Surface. cpp e bezier. Canoe. cpp que desenham superfícies de Bézier usando comandos de Open. GL. Explique os comandos que geram as superfícies em ambos programas.

Modelagem de Sólidos

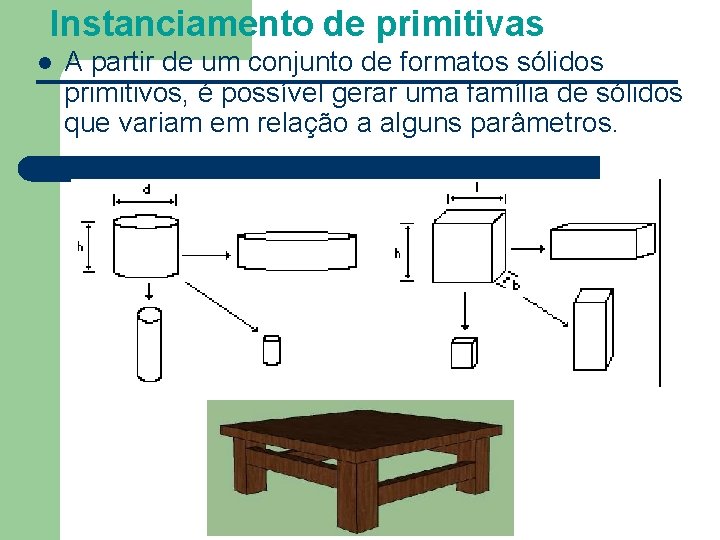
Instanciamento de primitivas l A partir de um conjunto de formatos sólidos primitivos, é possível gerar uma família de sólidos que variam em relação a alguns parâmetros.

Instanciamento de primitivas l - No Open. GL pode-se usar como primitivas: Primitivas da GLUT Primitivas quádricas da GLU

Primitivas da GLUT A biblioteca GLUT oferece uma coleção de objetos disponíveis em modo sólido e aramado. void glut. Wire. Sphere(GLdouble radius, GLint slices, GLint stacks); lvoid glut. Solid. Sphere(GLdouble radius, GLint slices, GLint stacks); lvoid glut. Wire. Cube(GLdouble size); lvoid glut. Solid. Cube(GLdouble size); lvoid glut. Wire. Cone(GLdouble radius, GLdouble height, GLint slices, GLint stacks); lvoid glut. Solid. Cone(idem); lvoid glut. Wire. Torus(GLdouble inner. Radius, GLdouble outer. Radius, GLint nsides, GLint rings); lvoid glut. Solid. Torus(GLdouble inner. Radius, GLdouble outer. Radius, GLint nsides, GLint rings);

Primitivas da GLUT lvoid glut. Wire. Dodecahedron(GLdouble radius); lvoid glut. Solid. Dodecahedron(GLdouble radius); lvoid glut. Wire. Octahedron(void); lvoid glut. Solid. Octahedron(void); lvoid glut. Wire. Tetrahedron(void); lvoid glut. Solid. Tetrahedron(void); lvoid glut. Wire. Icosahedron(void); lvoid glut. Solid. Icosahedron(void); lvoid glut. Wire. Teapot(GLdouble size); lvoid glut. Solid. Teapot(GLdouble size); Veja e rode o programa glut. Objects. cpp da pasta Code

Quádricas da GLU A biblioteca GLU provê a renderização automática de objetos tridimensionais como esferas, cilindros e discos. l Esferas: glu. Sphere(GLUquadric. Obj *obj, GLdouble radius, GLint slices, Glint stacks) l Cilindros: glu. Cylinder(GLUquadric. Obj *obj, GLdouble base. Radius, Gldouble top. Radius, GLdouble height, GLint slices, GLint stacks) top. Radius == zero, permite criar cone. l Discos: glu. Disk(GLUquadric. Obj *obj, GLdouble inner. Radius, GLdouble outer. Radius, GLint slices, GLint loops) inner. Radius != zero, permite criar discos com furos. Veja e rode o programa glu. Quadrics. cpp da pasta Code

Superfícies Bézier em Open. GL Leia e entenda o programa torpedo. cpp que desenha um torpedo composto de diferentes pedaços: (i) Corpo: cilindro da GLU (ii) Nariz: hemisferio (iii) Três barbatanas: discos parciais da GLU (iv) Disco traseiro : disco da GLU (v) Haste da hélice: cilindro da GLU (vi) Três pás da hélice: pedaços bicúbicos Bezier 2. Desenhe um avião composto de vários pedaços. Use superfícies de Bézier e quádricas. 1.

Superfícies Bézier e quádricas em Open. GL 3. Modele os seguintes objetos.

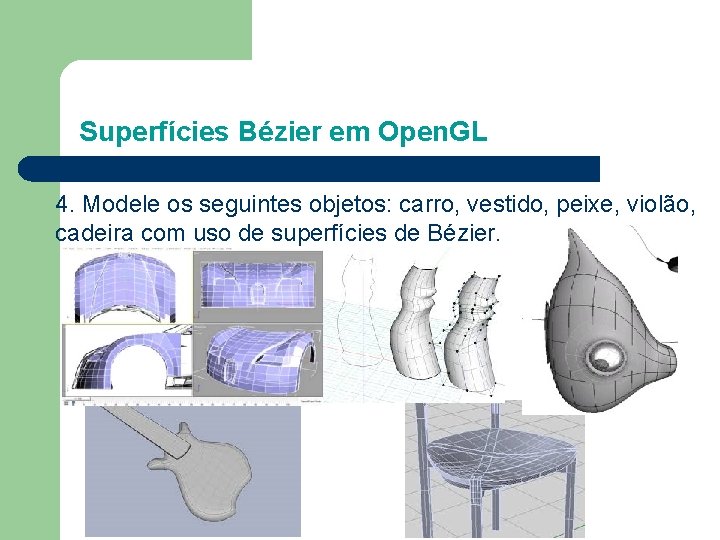
Superfícies Bézier em Open. GL 4. Modele os seguintes objetos: carro, vestido, peixe, violão, cadeira com uso de superfícies de Bézier.

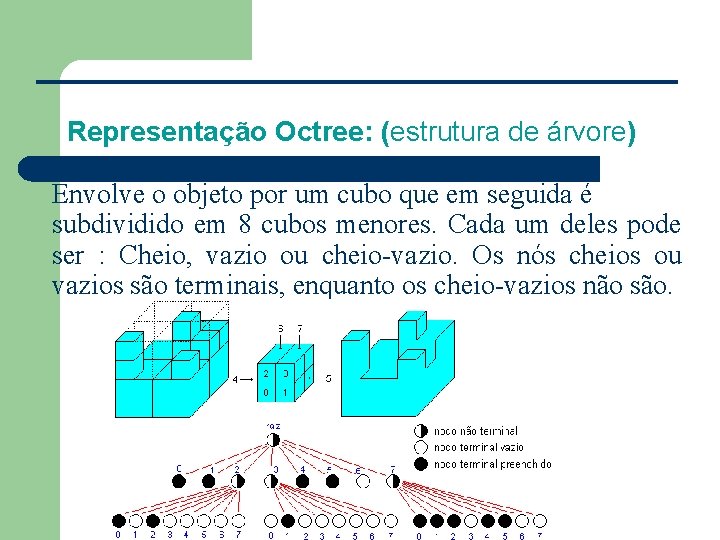
Representação Octree: (estrutura de árvore) Envolve o objeto por um cubo que em seguida é subdividido em 8 cubos menores. Cada um deles pode ser : Cheio, vazio ou cheio-vazio. Os nós cheios ou vazios são terminais, enquanto os cheio-vazios não são.

Representação Octree: Exemplo

Representação Octree: Exemplo

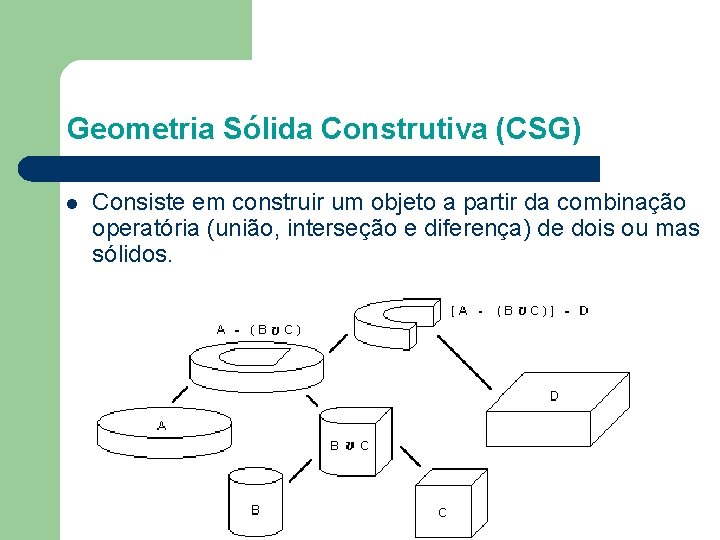
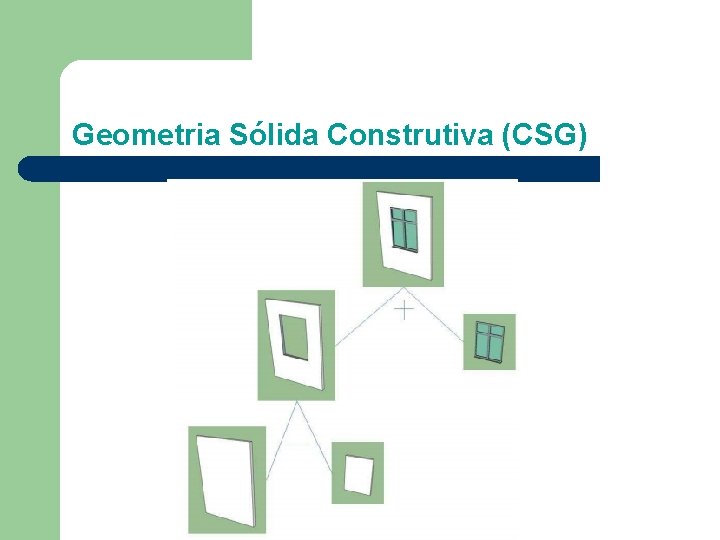
Geometria Sólida Construtiva (CSG) l Consiste em construir um objeto a partir da combinação operatória (união, interseção e diferença) de dois ou mas sólidos.

Geometria Sólida Construtiva (CSG)

Geometria Sólida Construtiva (CSG)

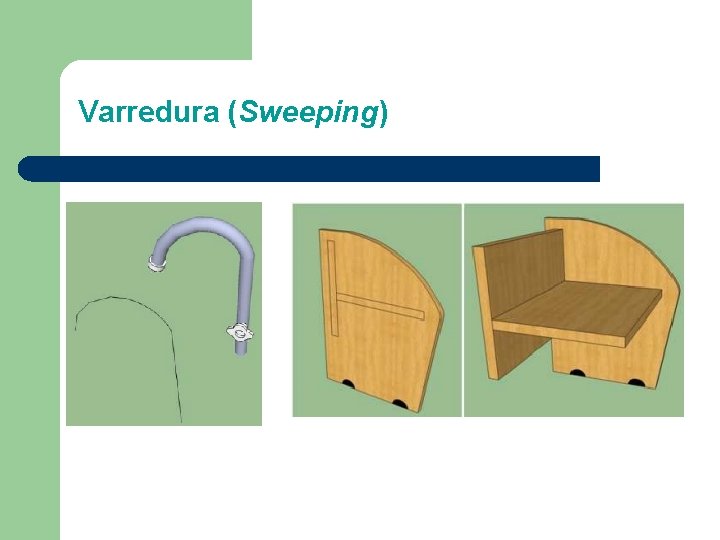
Varredura (Sweeping) Uma superfície é descrita quando uma curva C 1 (curva geratriz) é deslocada no espaço, ao longo de uma trajetória dada por uma outra curva C 2 (caminho o diretriz). - Varredura translacional (Extrusão ou superfícies geradas por deslocamento) l

Varredura (Sweeping)

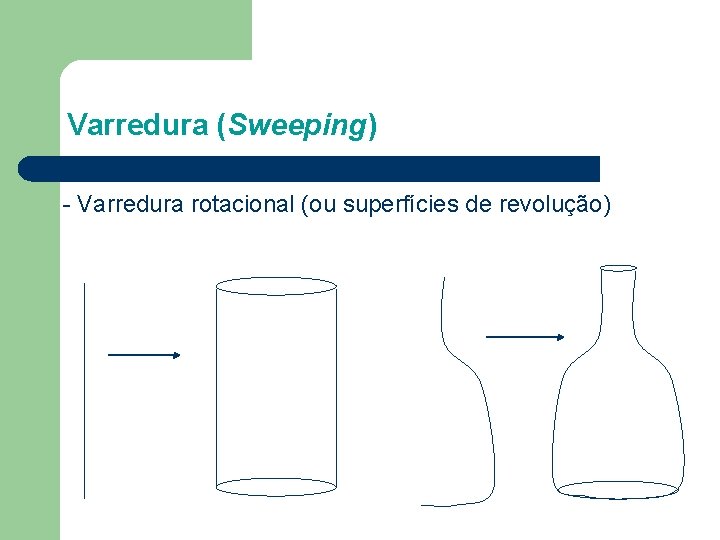
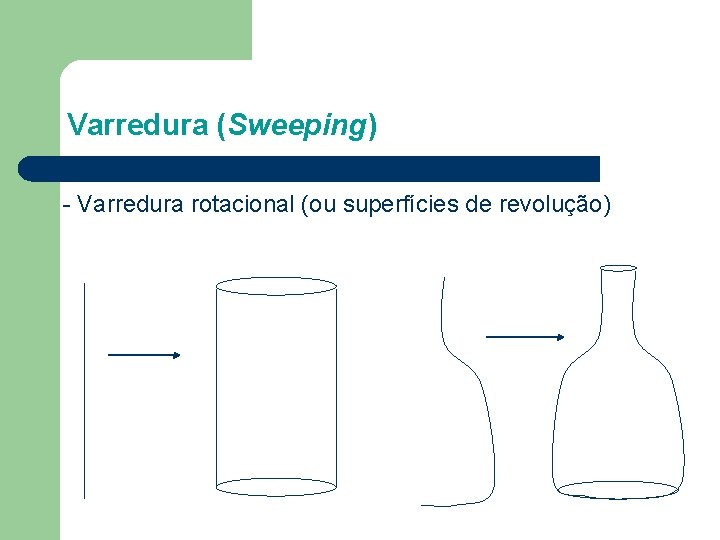
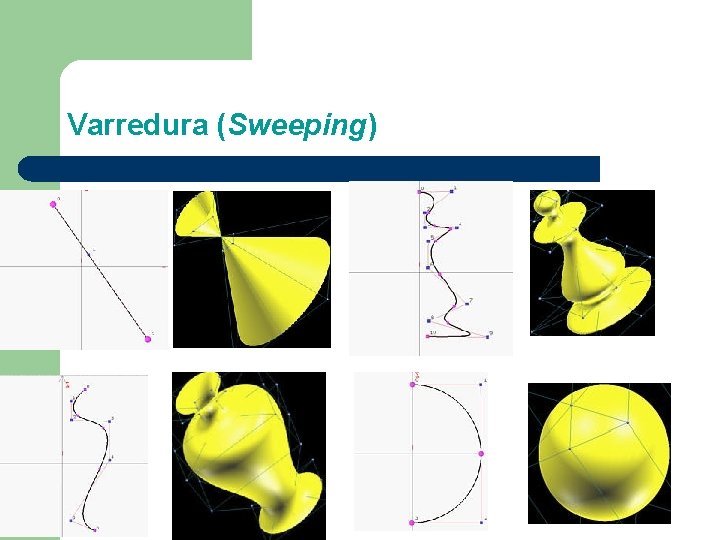
Varredura (Sweeping) - Varredura rotacional (ou superfícies de revolução)

Varredura (Sweeping) - Varredura rotacional (ou superfícies de revolução)

Varredura (Sweeping)

Superfície de Revolução - Tarefa O executável swprj. exe permite desenhar uma curva geratriz que dará origem a uma superfície de revolução § O programa torus. c (disponível no site da disciplina) desenha a superfície de revolução chamada torus. § O programa superfícies. cpp permite desenhar uma curva de Bézier como curva geratriz e a partir dela obter uma superfície de revolução. (1) Veja que a superfície em superfícies. cpp é representada apenas por cortes horizontais, como você representaria ela por polígonos (quadriláteros ou triângulos)? §

Superfície de Revolução - Tarefa (2) Compare o programa torus. cpp da pasta Code com o programa torus. c disponibilizado no site da disciplina. Para consulta de comandos novos use o livro Red. Book disponibilizado também no site da disciplina. (3) Desenhar um cilindro como superfície de revolução usando um segmento de reta como curva geratriz.

Malha de Polígonos - Coleções de polígonos (ou faces) que, juntos, formam a “pele” ou “casca” do objeto • Forma rápida e prática para representar objetos Estrutura de Dados. Lista contígua das coordenadas de todos os vértices que compõem cada face. - Arestas implícitas - Faces explícitas

Malha de Polígonos
 Mercedes gonzales
Mercedes gonzales He aprendido que cuando un recien nacido aprieta
He aprendido que cuando un recien nacido aprieta Bibliografia de gabriel garcia marquez
Bibliografia de gabriel garcia marquez Se despide un genio gabriel garcia marquez
Se despide un genio gabriel garcia marquez Funciones lineales
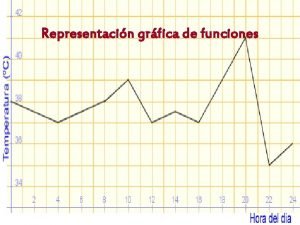
Funciones lineales Grfica
Grfica Función escalonada significado
Función escalonada significado Internet profa
Internet profa Profa ma
Profa ma Internet profa
Internet profa Multiplicaciones con decimales
Multiplicaciones con decimales Www.profa
Www.profa Profa campis
Profa campis Estudia la naturaleza
Estudia la naturaleza Geomtrica
Geomtrica Trino logos solar
Trino logos solar Media armonica formula
Media armonica formula Ejercicios de espejos
Ejercicios de espejos Geomtrica
Geomtrica Exemplo de progressão geométrica
Exemplo de progressão geométrica Geomtrica
Geomtrica Modelagem de dados
Modelagem de dados Modelagem
Modelagem Modelagem de trabalho
Modelagem de trabalho Modelagem
Modelagem Modelagem olap
Modelagem olap Modelagem
Modelagem Neal martin maura gonzales
Neal martin maura gonzales Dne correios download 2021
Dne correios download 2021 Geisha gonzales
Geisha gonzales Ferramentas case utilizados para modelagem de dados
Ferramentas case utilizados para modelagem de dados Speedy gonzales
Speedy gonzales Propiedades fisicas y quimicas del fosforo
Propiedades fisicas y quimicas del fosforo Modelagem caixa branca
Modelagem caixa branca Katangian ng mabuting talakayan
Katangian ng mabuting talakayan 3 sounds of y
3 sounds of y Bidy gonzales plant
Bidy gonzales plant Modelagem
Modelagem Reforma financiera de alfredo gonzález flores
Reforma financiera de alfredo gonzález flores Vladimeir gonzales
Vladimeir gonzales Modelagem dimensional
Modelagem dimensional Gonzalez and woods
Gonzalez and woods Tourbillon de passions mauricio gonzáles
Tourbillon de passions mauricio gonzáles Glaucio gonzales
Glaucio gonzales Modelagem
Modelagem Sistemas de controle
Sistemas de controle Adolfo gonzales chief probation officer
Adolfo gonzales chief probation officer Colegio maria mercedes carranza
Colegio maria mercedes carranza Colegio integrado nuestra señora de las mercedes
Colegio integrado nuestra señora de las mercedes Mercedes rueda lizana
Mercedes rueda lizana Mercedes cano herrera
Mercedes cano herrera Gmail
Gmail