Computability and Complexity 6 1 Rices Theorem Computability

Computability and Complexity 6 -1 Rice’s Theorem Computability and Complexity Andrei Bulatov

Computability and Complexity 6 -2 Computation about Computation We have seen that some problems concerning operation of TMs and other computational models are undecidable In this lecture we shall see that this is an inherent property of all problems about computation We show that the question “Does my program do what I want it to do? ” is normally undecidable

Computability and Complexity 6 -3 Known Undecidable Problems HALTING Instance: A Turing Machine T and an input string x. Question: Does T(x) halt? ACCEPTANCE Instance: A Turing Machine (acceptor) T and an input string x. Question: Does T accept x?

Computability and Complexity More Undecidable Problems EMPTINESS Instance: A Turing Machine T. Question: Is the language L(T) empty? FULLNESS Instance: A Turing Machine T. Question: Is the language L(T) equal to *? The corresponding languages are: 6 -4

Computability and Complexity Theorem and 6 -5 are undecidable. Proof We show that For every input “T; x” of an input y as follows: • • , let S be a machine operating on Erase input y Write x on the tape Simulate T on x If T(x) halts then “Accept”

Computability and Complexity 6 -6 Observe that • If T halts on x, then L(S)= * (i. e. , S accepts every input y • If T does not halt on x, then L(S)= ? This function is computable and total QED

Computability and Complexity A proof of is similar 6 -7

Computability and Complexity 6 -8 The EQUIVALENCE Problem EQUIVALENCE Instance: Turing Machines Question: and ? The corresponding language is: Theorem Proof - see next slide is undecidable. .

Computability and Complexity 6 -9 We show that Fix a TM with For every input “T” of , define an input of Then L(T)= if and only if QED as

Computability and Complexity 6 -10 Properties of TMs Usually, a problem can be solved in many different ways. There are many (different) programs with indistinguishable behavio Definition A collection, R, of TM descriptions is called - a property if, for any TMs and then either and are in R, or and are not in R , if - a non-trivial property if there exists a TM which is in R and there exists a TM which is not in R

Computability and Complexity Examples • Does a TM halt on every input? • Does a TM accepts any input? (FULLNESS) • Does a TM rejects any input? • Does a TM output the sum of two given naturals? • Does a TM accept only strings longer than 3 symbols? • Does a TM ever leave its initial state? • Does a TM print its own description? (EMPTYNESS) 6 -11

Computability and Complexity Rice’s Theorem Any non-trivial property of TMs is undecidable. 6 -12

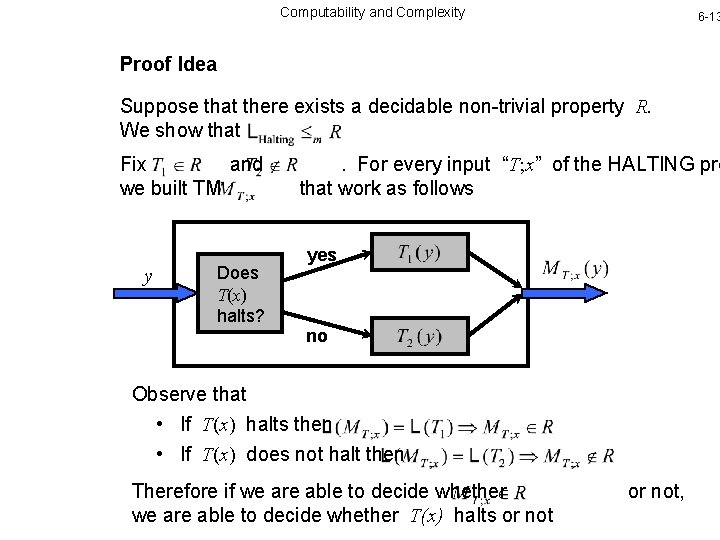
Computability and Complexity 6 -13 Proof Idea Suppose that there exists a decidable non-trivial property R. We show that Fix and we built TM y Does T(x) halts? . For every input “T; x” of the HALTING pro that work as follows yes no Observe that • If T(x) halts then • If T(x) does not halt then Therefore if we are able to decide whether T(x) halts or not,

Computability and Complexity Case 1. There is a TM For every input “T; x” of an input y as follows: 6 -14 such that , let be a machine operating • Simulate T on x • If T(x) terminates, simulate Then • If T(x) halts then • If T(x) does not halt then on y

Computability and Complexity Case 2. There is a TM For every input “T; x” of an input y as follows: 6 -15 such that , let be a machine operating • Simulate T on x • If T(x) terminates, simulate Then • If T(x) halts then • If T(x) does not halt then on y

Computability and Complexity Example Let e be a graph encoding scheme and L={x | x is the code of a Hamilton graph} Property R={T | L(T)=L} Then the question “Does a TM possess property R? ” = “Does my program recognises Hamiltonian graphs? ” is undecidable! It is impossible to automatize software verification 6 -16