COMPUNEREA VECTORILOR Vectorii se pot compune folosind Metode

COMPUNEREA VECTORILOR

Vectorii se pot compune folosind : • Metode geometrice • Metoda analitică

A) Metodele geometrice sunt : Ø Regula paralelogramului Ø Regula triungiului Ø Regula poligonului

REGULA PARALELOGRAMULUI Regula paralelogramului este cea mai cunoscută metodă de compunere a doi vectori concurenţi. A compune vectorii a şi b înseamnă a găsi modulul şi orientarea vectorului rezultant : c = a + b.

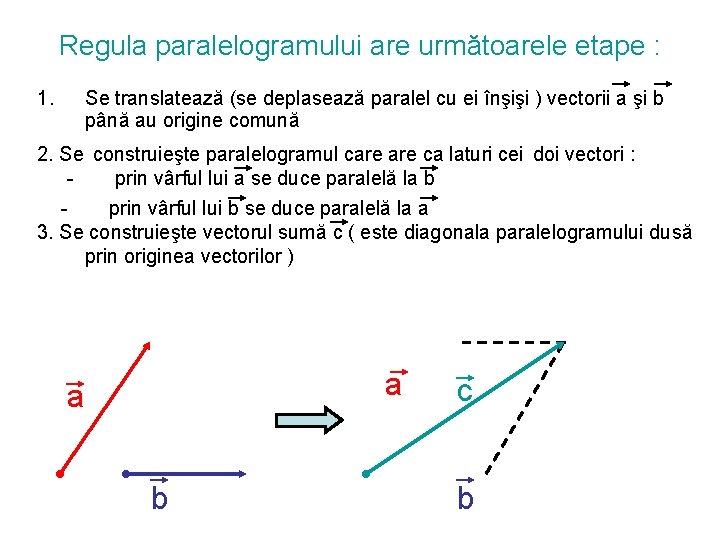
Regula paralelogramului are următoarele etape : 1. Se translatează (se deplasează paralel cu ei înşişi ) vectorii a şi b până au origine comună 2. Se construieşte paralelogramul care ca laturi cei doi vectori : prin vârful lui a se duce paralelă la b prin vârful lui b se duce paralelă la a 3. Se construieşte vectorul sumă c ( este diagonala paralelogramului dusă prin originea vectorilor ) a a b c b

Vectorul sumă c are următoarele caracteristici : - originea comună cu originile celor doi vectori a şi b ; - direcţia de-a lungul diagonalei paralelogramului ; - sensul dat de săgeată ; - modulul egal cu lungimea diagonalei paralelogramului.

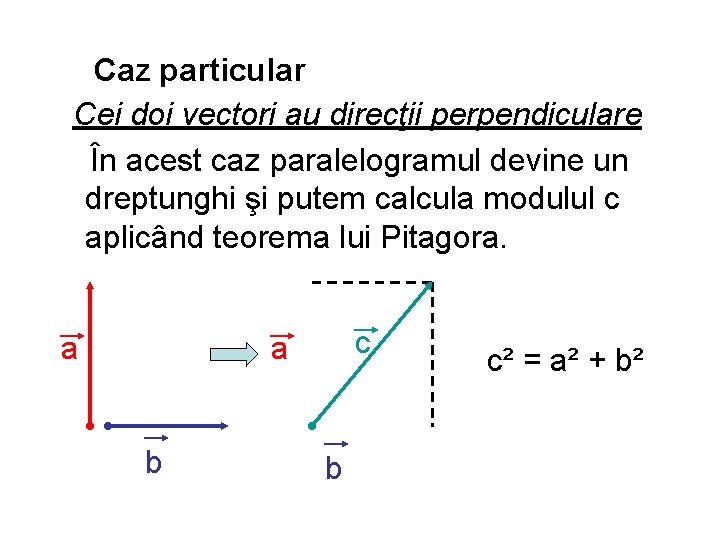
Caz particular Cei doi vectori au direcţii perpendiculare În acest caz paralelogramul devine un dreptunghi şi putem calcula modulul c aplicând teorema lui Pitagora. a c a b b c² = a² + b²

REGULA TRIUNGHIULUI Regula triunghiului este o metodă de compunere a doi vectori. Regula triunghiului are următoarele etape: 1. Se translatează un vector ( b ) până când originea lui va fi în vârful celuilalt vector ( a ) 2. Se uneşte originea primului vector a cu vârful lui b şi se obţine vectorul sumă c a a c b b

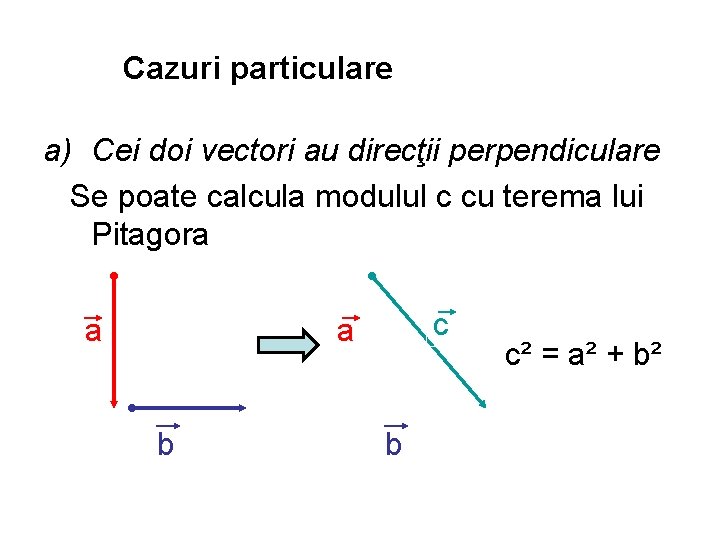
Cazuri particulare a) Cei doi vectori au direcţii perpendiculare Se poate calcula modulul c cu terema lui Pitagora a c a b b c² = a² + b²

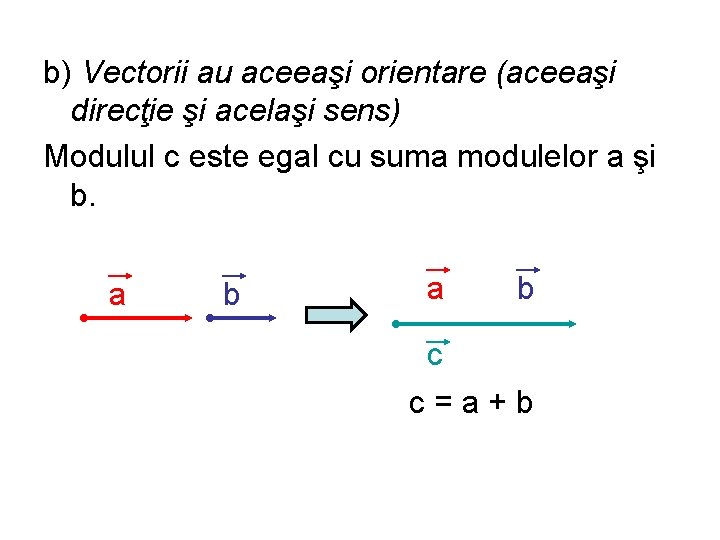
b) Vectorii au aceeaşi orientare (aceeaşi direcţie şi acelaşi sens) Modulul c este egal cu suma modulelor a şi b. a b c c=a+b

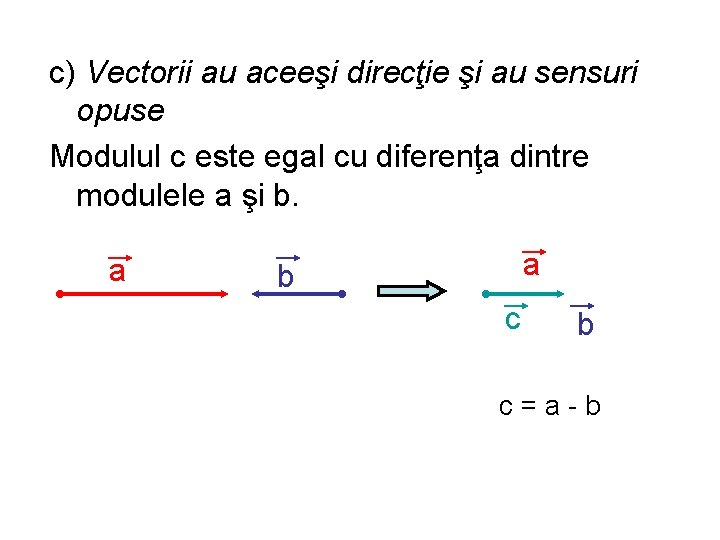
c) Vectorii au aceeşi direcţie şi au sensuri opuse Modulul c este egal cu diferenţa dintre modulele a şi b. a a b c=a-b

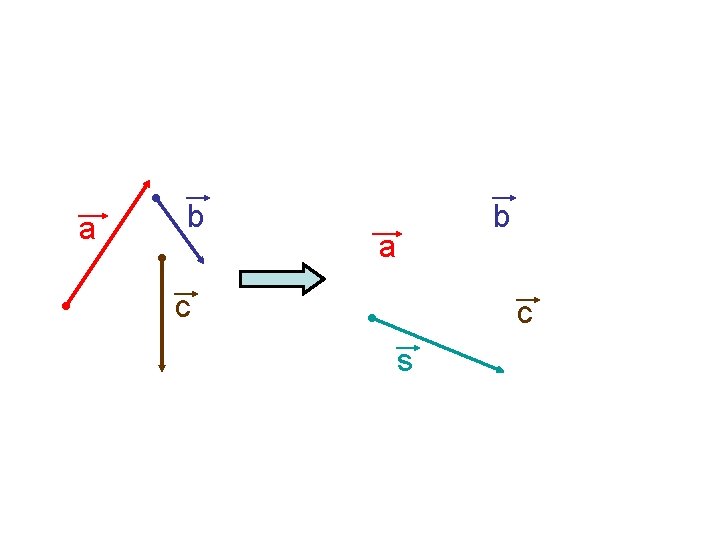
REGULA POLIGONULUI Regula poligonului este folosită pentru a aduna 3 sau mai mulţi vectori. Etapele sunt : 1. Se translatează vectorul b cu originea în vârful vectorului a , apoi se translatează vectorul c cu originea în vârful vectorului b şi mai departe 2. Vectorul sumă s uneşte originea primului vector cu vârful ultimului vector

a b b a c c s

B) Metoda analitică Metoda anlitică este folosită pentru a aduna doi sau mai mulţi vectori. Etapele metodei sunt : 1. Se alege un sistem de două axe de coordonate xoy 2. Se proiectează vectorii pe axe şi se calculează componentele lor (folosind funcţiile trigonometrice )

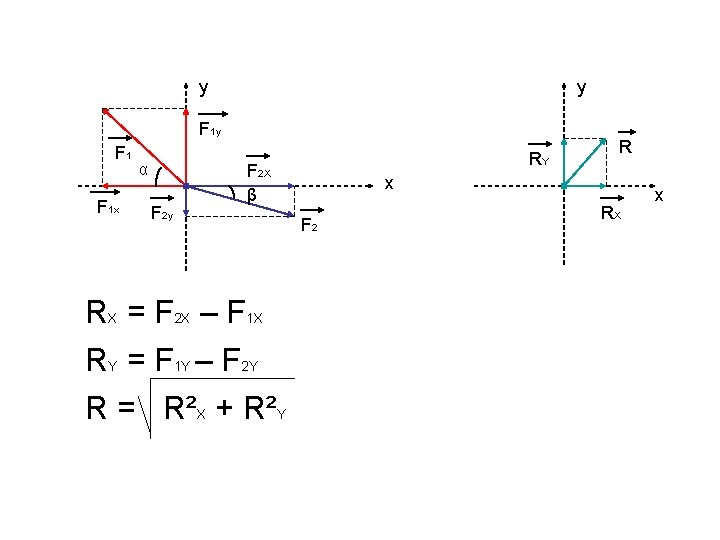
3. Se calculează componentele vectorului sumă de pe cele două axe (sumă algebrică). Proiecţiile din sensul pozitiv al axei se iau cu semnul “+”, celălalte se iau cu semnul “-”. 4. Se calculează modulul vectorului rezultant cu relaţia : R = R² + R²

y y F 1 F 1 x α F 2 y RY F 2 X β RX = F 2 X – F 1 X RY = F 1 Y – F 2 Y R = R²X + R²Y R x F 2 RX x

SF RŞIT • Realizat de TOBĂ NICOLETA