COMPSCI 330 Design and Analysis of Algorithms Rong

COMPSCI 330 Design and Analysis of Algorithms Rong Ge

Logistics • Lectures: Tuesdays and Thursdays 3: 05 - 4: 20 PM • Recitations: Check your own schedule • Recitations are required! • First week: Optional (Review of Induction) Students in Friday morning sessions should all go to LSRC D 106. • Webpage: http: //www. cs. duke. edu/courses/spring 19/compsci 330/ • Office hours: Tuesday after class to 5: 30 pm Friday at 3 – 4 pm • TA office hours: See course webpage

Grades • Homework 40% • 2 Midterms 30% • Final Exam 30% • Homework should be typed and submitted to Gradescope. • Read (and follow) the guideline on collaboration. • Go to office hours!

STINF, Exam conflicts • Kate O’Hanlon is our teaching associate. • Email: kate. o. hanlon@duke. edu • Please take a look at the tentative schedule and if you have a conflict for any of the exams please let Kate know as early as possible. • For STINF please use a web form (will be posted on piazza later).

Contact us • Piazza: http: //piazza. com/duke/spring 2019/compsci 330 Please use for all general discussions. • Piazza is required! All announcements will be on Piazza. • Grading questions: Please submit regrade requests through Grade. Scope. Homework requests will be handled by grad TAs and exam requests will be handled by myself. • Send me an email: rongge@cs. duke. edu

Lecture format • Slides first, then go to the board (tablet). • Best way of learning a proof is to write it down yourself. • I will try to record the lectures – hopefully the technology does not fail.

Algorithms • From wiki: In mathematics and computer science, an algorithm is a self-contained sequence of actions to be performed.

Designing an Algorithm - Basics • Divide and conquer • Dynamic programming • Greedy algorithms

Designing an Algorithm - Examples • Graph algorithms • Shortest paths • Minimum spanning tree • Bipartite matching • Data structrues • Hashing • Disjoint sets

Designing Algorithm – General Tools • Linear Programming • Formulation • Duality • Algorithms

Designing Algorithm - Intractability • What (we believe) cannot have efficient algorithms. • P vs. NP • NP completeness • Reductions

Analysis - Proofs • Proof: Systematic way of convincing the reader that a mathematical statement is necessarily correct. • Writing proofs is a major component of this course.

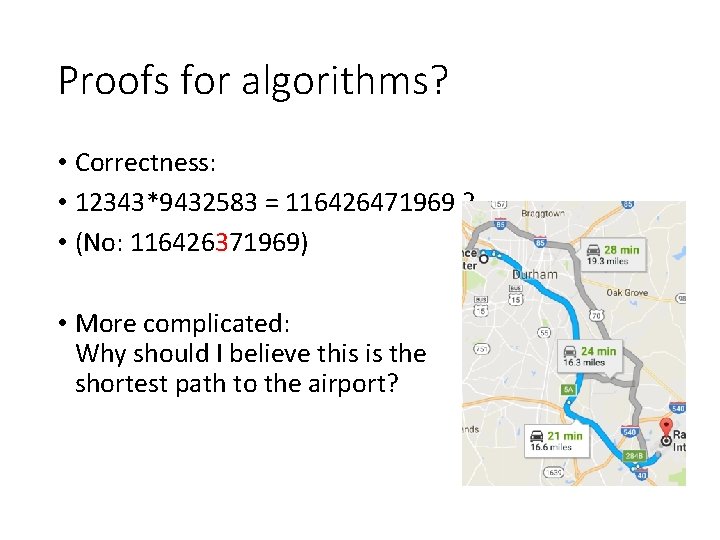
Proofs for algorithms? • Correctness: • 12343*9432583 = 116426471969 ? • (No: 116426371969) • More complicated: Why should I believe this is the shortest path to the airport?

Proofs for algorithms? • Running time: How long should the algorithm take. • Space: How much memory does the algorithm need.

Other aspects (not in this course) • Privacy/security

Other aspects (not in this course) • Fairness

Goal • Design new algorithms for applications you care. • Prove correctness/running time for algorithms.

How to write a proof? • Will see many examples in class. • Very similar to writing a program. Program • Unambiguous instructions for computers to solve a problem • Function/subroutine • System call/packages • Loop/Recursion • …… Proof • Unambiguous way of certifying a mathematical statement. • Lemma • Theorem • Induction • ……

Example • Prove that 1+2+3+… + n = n(n+1)/2 for all integers n. • Idea: Base Case • Prove(n) • Prove [1+…+k = k(k+1)/2] for k = 1 • For k = 1 to n-1 Induction Hypothesis • Show if [1+…+k = k(k+1)/2], then [1+…+k + (k+1) = (k+1)(k+2)/2] Induction Step

Rest of the lecture (on whiteboard) • Asymptotic notations • One of the earliest algorithms: Euclid’s algorithm