COMPSCI 230 Discrete Mathematics for Computer Science Counting

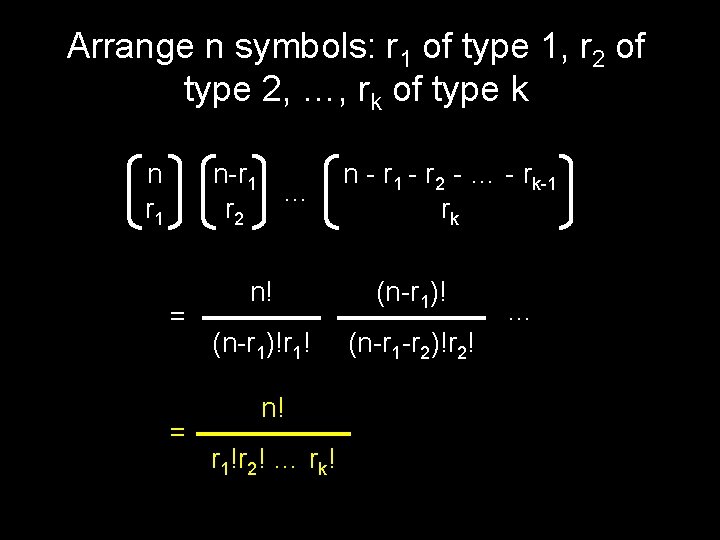



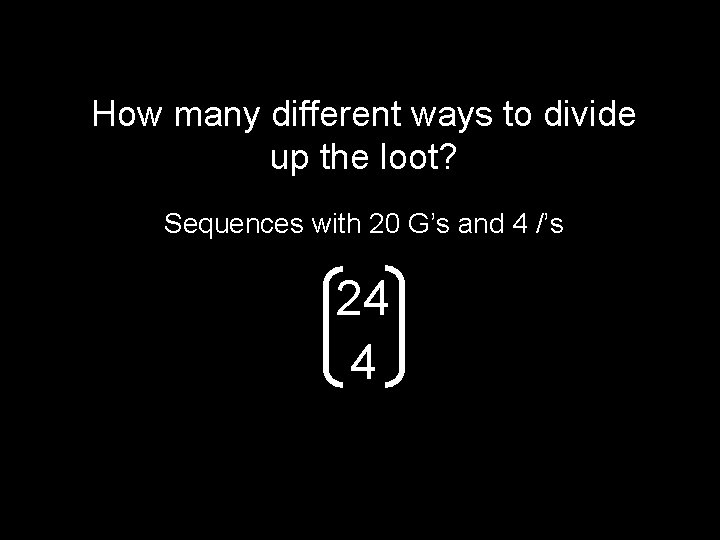











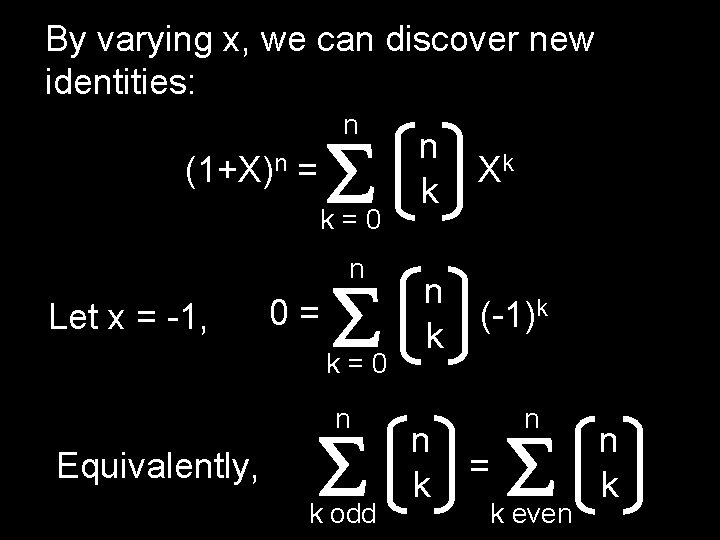























- Slides: 64

COMPSCI 230 Discrete Mathematics for Computer Science
Counting III Lecture 8 1 X+ 2 X+ 3 X

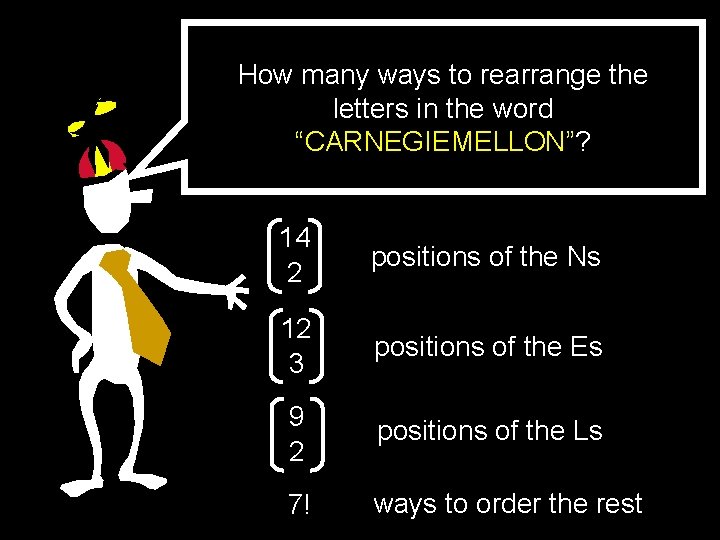
How many ways to rearrange the letters in the word “CARNEGIEMELLON”? 14 2 positions of the Ns 12 3 positions of the Es 9 2 positions of the Ls 7! ways to order the rest
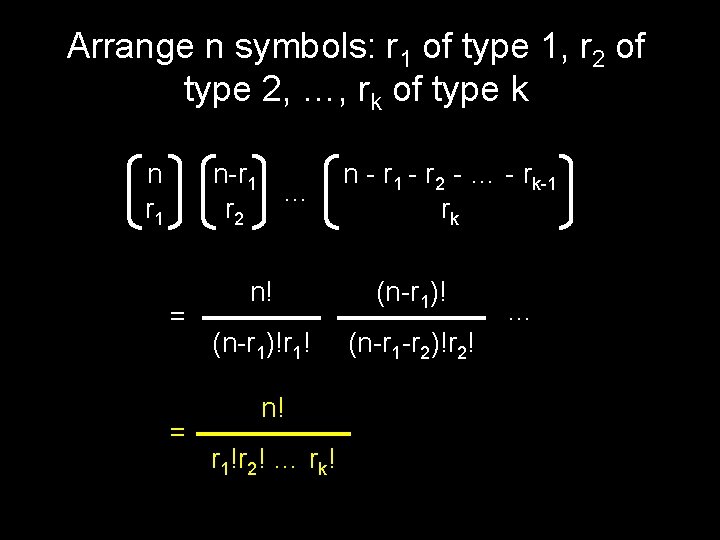
Arrange n symbols: r 1 of type 1, r 2 of type 2, …, rk of type k n-r 1 … r 2 n r 1 = = n - r 1 - r 2 - … - rk-1 rk n! (n-r 1)!r 1! (n-r 1 -r 2)!r 2! n! r 1!r 2! … rk! …

CARNEGIEMELLON 14! 2!3!2! = 3, 632, 428, 800

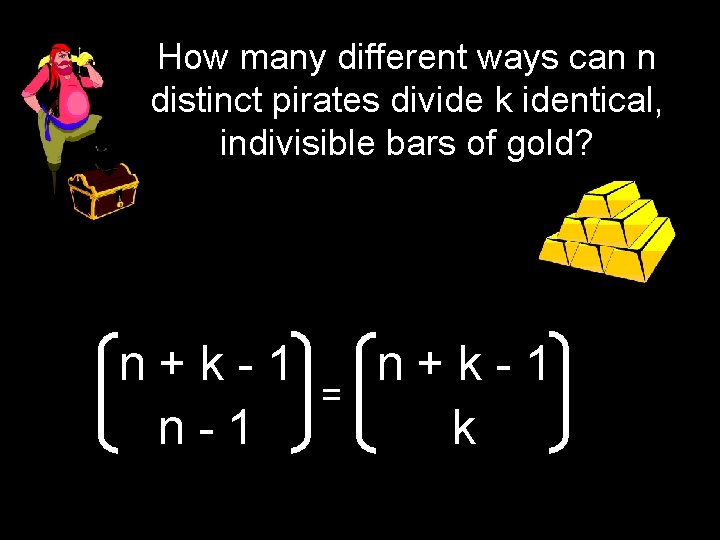
5 distinct pirates want to divide 20 identical, indivisible bars of gold. How many different ways can they divide up the loot?

Sequences with 20 G’s and 4 /’s GG/G//GGGGGGGGG/ represents the following division among the pirates: 2, 1, 0, 17, 0 In general, the ith pirate gets the number of G’s after the (i-1)st / and before the ith / This gives a correspondence (bijection) between divisions of the gold and sequences with 20 G’s and 4 /’s
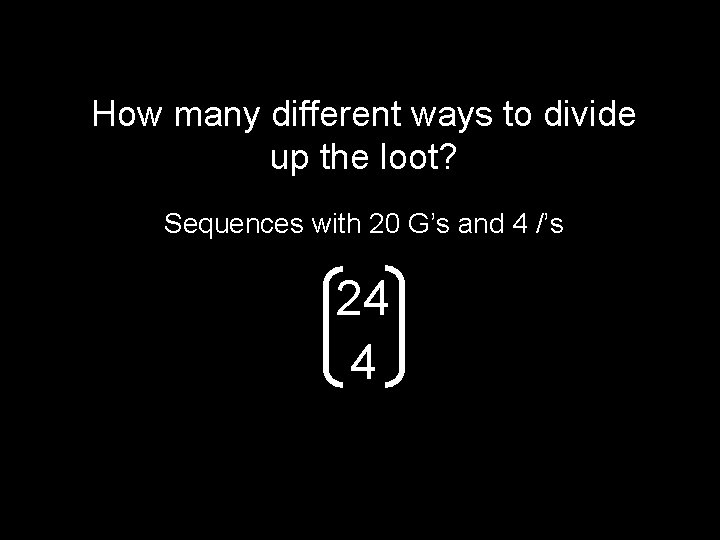
How many different ways to divide up the loot? Sequences with 20 G’s and 4 /’s 24 4

How many different ways can n distinct pirates divide k identical, indivisible bars of gold? n+k-1 n-1 = n+k-1 k

Identical/Distinct Dice Suppose that we roll seven dice How many different outcomes are there, if order matters? 67 What if order doesn’t matter? (E. g. , Yahtzee) 12 7 (Corresponds to 6 pirates and 7 bars of gold)

Multisets A multiset is a set of elements, each of which has a multiplicity The size of the multiset is the sum of the multiplicities of all the elements Example: {X, Y, Z} with m(X)=0 m(Y)=3, m(Z)=2 Unary visualization: {Y, Y, Y, Z, Z}

Counting Multisets There number of ways to choose a multiset of size k from n types of elements is: n+k-1 = n-1 k

Taking k items from a set of n Order matters, no repetition: Order matters, repetition allowed: Order doesn’t matter, no repetition: n! (n-k)! nk n k Order doesn’t matter, repetition allowed: n+k-1 k

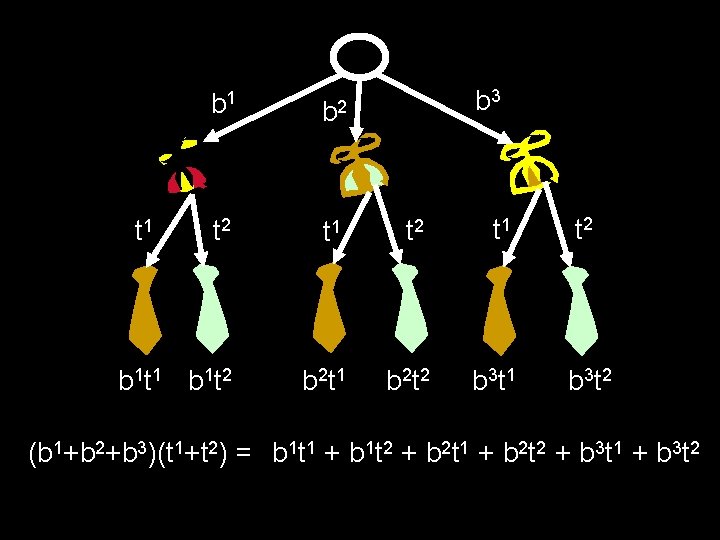
Polynomials Express Choices and Outcomes Products of Sum = Sums of Products ( + + + )( + + )= +

b 3 b 1 b 2 t 1 t 2 b 1 t 1 b 1 t 2 b 2 t 1 b 2 t 2 b 3 t 1 b 3 t 2 t 1 (b 1+b 2+b 3)(t 1+t 2) = b 1 t 1 + b 1 t 2 + b 2 t 1 + b 2 t 2 + b 3 t 1 + b 3 t 2

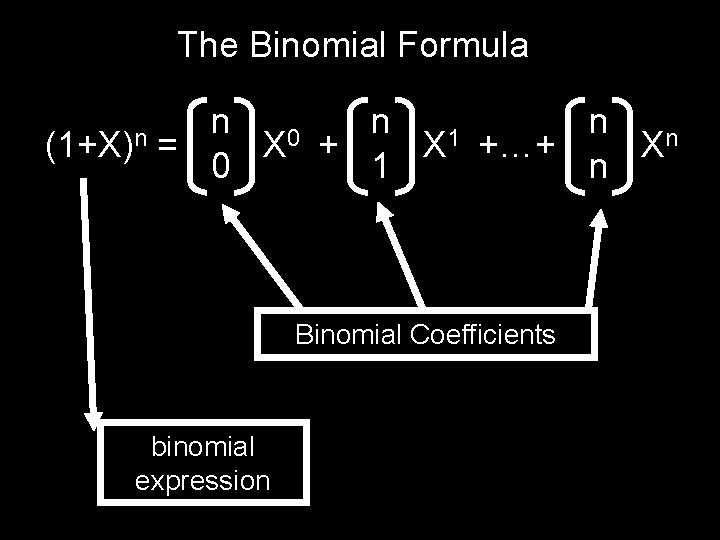
What is a Closed Form Expression For ck? (1+X)n = c 0 + c 1 X + c 2 X 2 + … + cn. Xn (1+X)(1+X)…(1+X) After multiplying things out, but before combining like terms, we get 2 n cross terms, each corresponding to a path in the choice tree ck, the coefficient of Xk, is the number of paths with exactly k X’s ck = n k

The Binomial Formula (1+X)n n 0 1 = X +…+ Xn 0 1 n Binomial Coefficients binomial expression

The Binomial Formula (1+X)0 = 1 (1+X)1 = 1 + 1 X (1+X)2 = 1 + 2 X + 1 X 2 (1+X)3 = 1 + 3 X 2 + 1 X 3 (1+X)4 = 1 + 4 X + 6 X 2 + 4 X 3 + 1 X 4

What is the coefficient of EMSTY in the expansion of (E + M + S + T + Y)5? 5!

What is the coefficient of EMS 3 TY in the expansion of (E + M + S + T + Y)7? The number of ways to rearrange the letters in the word SYSTEMS

What is the coefficient of (X 1 r 1 X 2 r 2…Xkrk) in the expansion of (X 1+X 2+X 3+…+Xk)n? n! r 1!r 2!. . . rk!

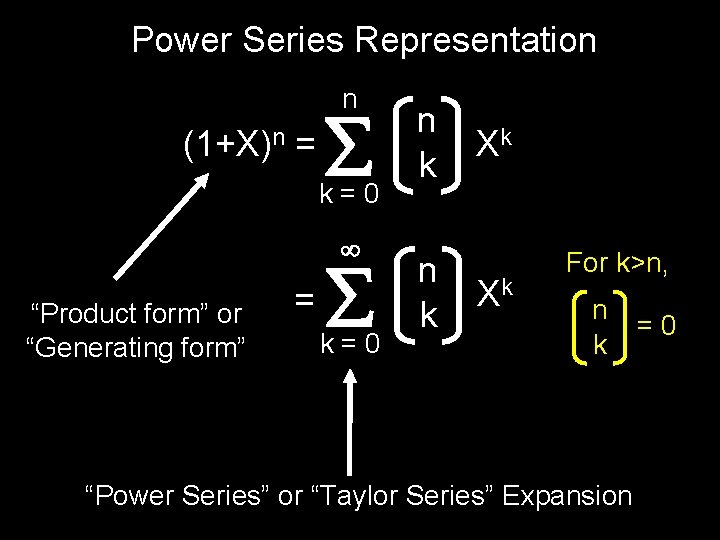
Power Series Representation n (1+X)n = k=0 “Product form” or “Generating form” = k=0 n k Xk Xk For k>n, n k “Power Series” or “Taylor Series” Expansion =0

By playing these two representations against each other we obtain a new representation of a previous insight: n (1+X)n = k=0 n Let x = 1, 2 n = k=0 n k Xk n k The number of subsets of an n-element set
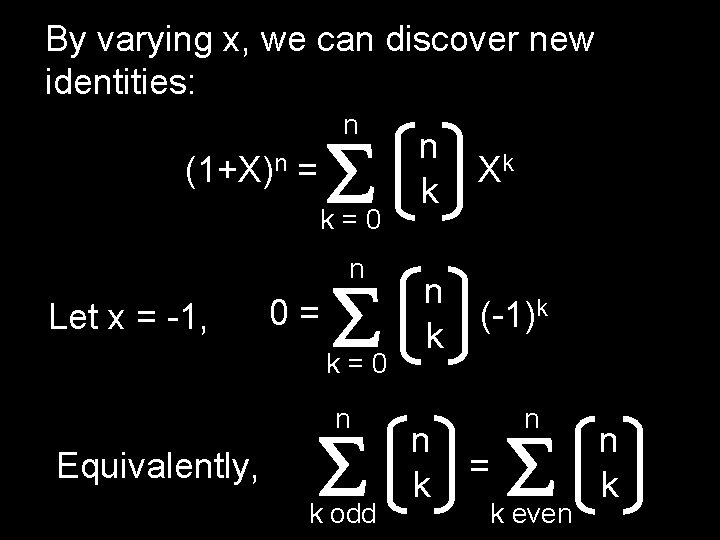
By varying x, we can discover new identities: n (1+X)n = k=0 n Let x = -1, 0= k=0 n Equivalently, k odd n k Xk n (-1)k k n = k even n k

The number of subsets with even size is the same as the number of subsets with odd size

n (1+X)n = k=0 n k Xk Proofs that work by manipulating algebraic forms are called “algebraic” arguments. Proofs that build a bijection are called “combinatorial” arguments

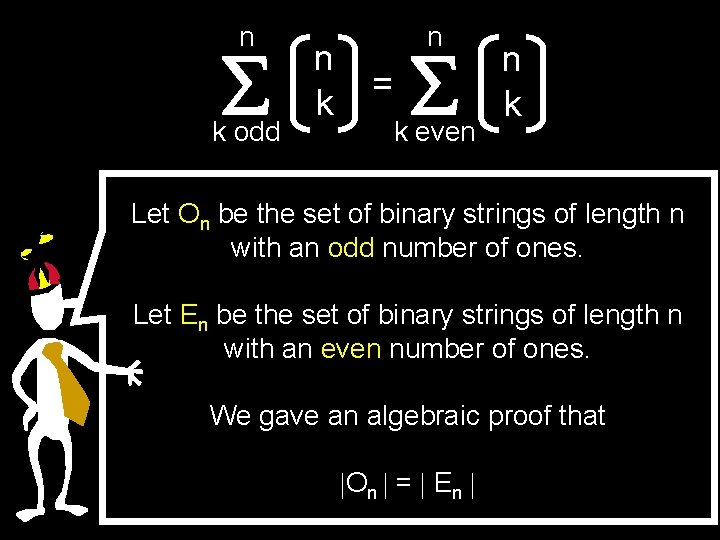
n k odd n k n = k even n k Let On be the set of binary strings of length n with an odd number of ones. Let En be the set of binary strings of length n with an even number of ones. We gave an algebraic proof that On = En

A Combinatorial Proof Let On be the set of binary strings of length n with an odd number of ones Let En be the set of binary strings of length n with an even number of ones A combinatorial proof must construct a bijection between On and En

An Attempt at a Bijection Let fn be the function that takes an n-bit string and flips all its bits fn is clearly a one-to-one and onto function for odd n. E. g. in f 7 we have: . . . but do even n work? In f 6 we have 0010011 1101100 1001101 0110010 110011 001100 101010 010101 Uh oh. Complementing maps evens to evens!

A Correspondence That Works for all n Let fn be the function that takes an n-bit string and flips only the first bit. For example, 0010011 101001101 0001101 110011 010011 101010 001010

n (1+X)n = k=0 n k Xk The binomial coefficients have so many representations that many fundamental mathematical identities emerge…

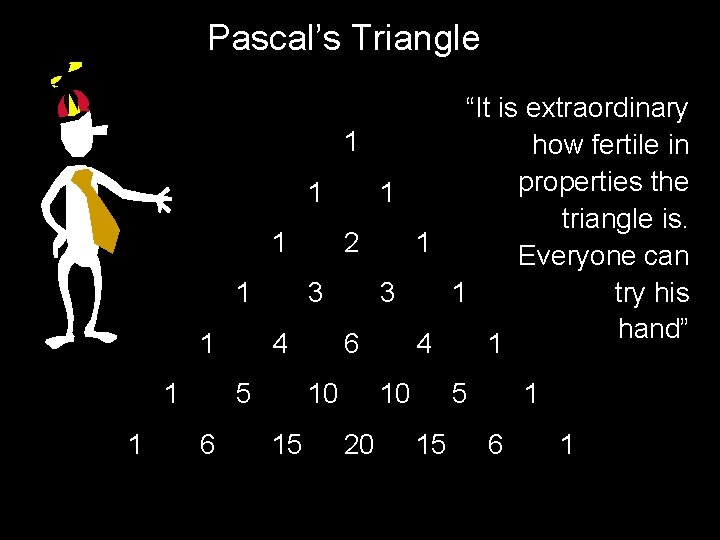
The Binomial Formula (1+X)0 = 1 (1+X)1 = 1 + 1 X (1+X)2 = 1 + 2 X + 1 X 2 (1+X)3 = 1 + 3 X 2 + 1 X 3 (1+X)4 = 1 + 4 X + 6 X 2 + 4 X 3 + 1 X 4 Pascal’s Triangle: kth row are coefficients of (1+X)k Inductive definition of kth entry of nth row: Pascal(n, 0) = Pascal (n, n) = 1; Pascal(n, k) = Pascal(n-1, k-1) + Pascal(n-1, k)

“Pascal’s Triangle” 0 =1 0 1 =1 0 2 =1 0 3 =1 0 1 =1 1 2 =2 1 3 =3 1 2 =1 2 3 =3 2 • Al-Karaji, Baghdad 953 -1029 • Chu Shin-Chieh 1303 • Blaise Pascal 1654 3 =1 3

Pascal’s Triangle “It is extraordinary 1 how fertile in properties the 1 1 triangle is. 1 2 1 Everyone can try his 1 3 3 1 hand” 1 4 6 4 1 1 1 5 6 10 15 10 20 5 15 1 6 1

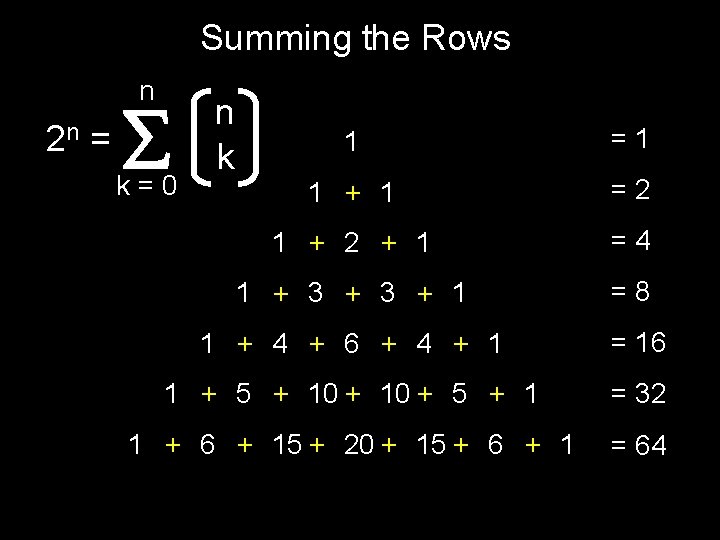
Summing the Rows n 2 n = n k 1 =1 1 + 1 =2 1 + 2 + 1 =4 1 + 3 + 1 =8 1 + 4 + 6 + 4 + 1 = 16 1 + 5 + 10 + 5 + 1 = 32 1 + 6 + 15 + 20 + 15 + 6 + 1 = 64 k=0

Odds and Evens 1 1 1 1 2 3 4 5 6 1 3 6 10 15 1 1 4 10 20 1 5 15 1 6 1 + 15 + 1 = 6 + 20 + 6 1

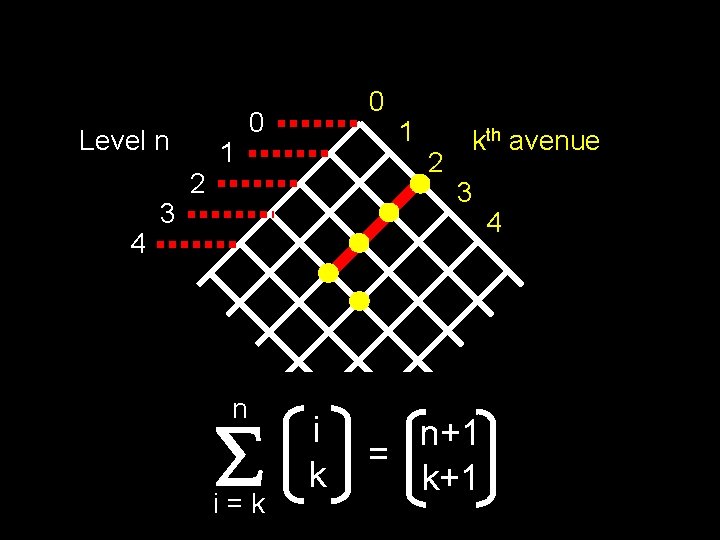
Summing on 1 st Avenue n 1 1 1 1 2 3 4 5 6 1 15 1 4 10 1 5 15 1 6 i=1 1 6 20 i = i=1 3 10 n 1 i = n+1 2 1

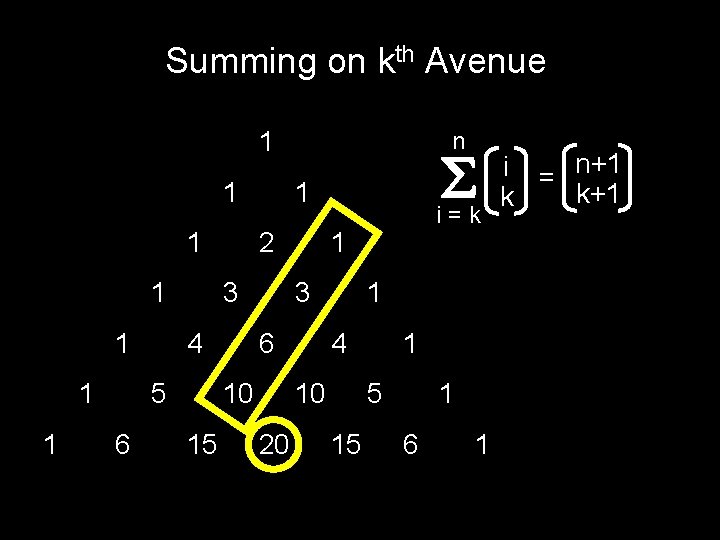
Summing on kth Avenue 1 1 1 1 6 2 4 6 1 4 10 20 i=k 1 3 10 15 1 3 5 n 1 5 15 1 6 1 i = n+1 k

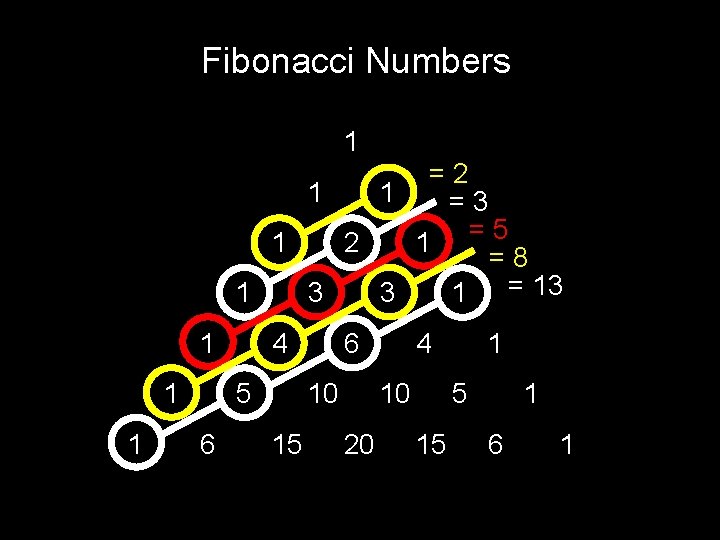
Fibonacci Numbers 1 =2 1 1 =3 = 5 1 2 1 =8 1 3 3 1 = 13 1 1 1 4 5 6 6 10 15 4 10 20 1 5 15 1 6 1

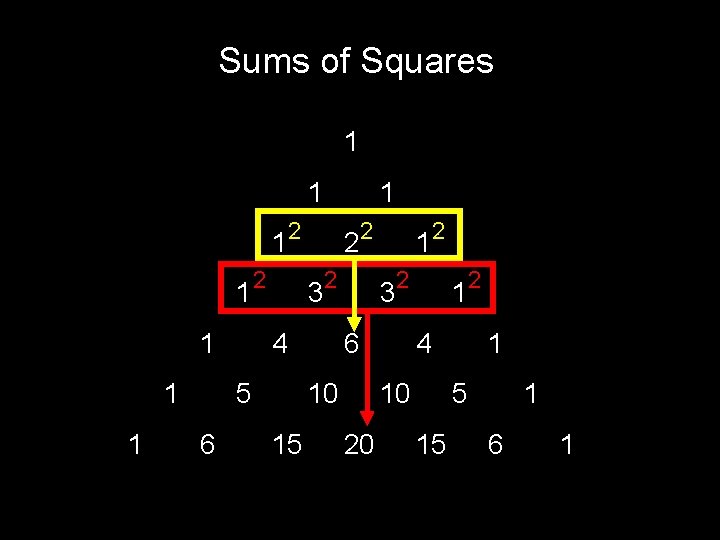
Sums of Squares 1 1 1 1 2 2 2 3 2 2 4 5 6 1 3 2 6 10 15 1 2 1 4 10 20 2 1 5 15 1 6 1

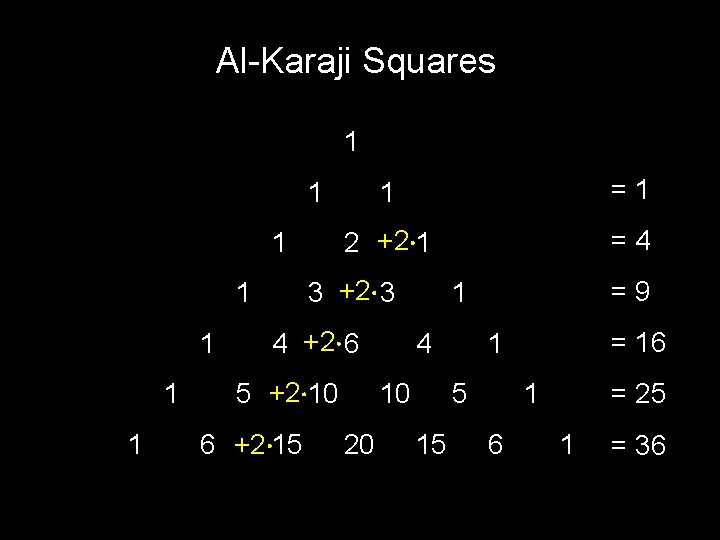
Al-Karaji Squares 1 1 =1 2 +2 1 =4 1 1 3 +2 3 1 1 4 +2 6 5 +2 10 6 +2 15 4 10 20 =9 1 5 15 = 16 1 1 6 = 25 1 = 36

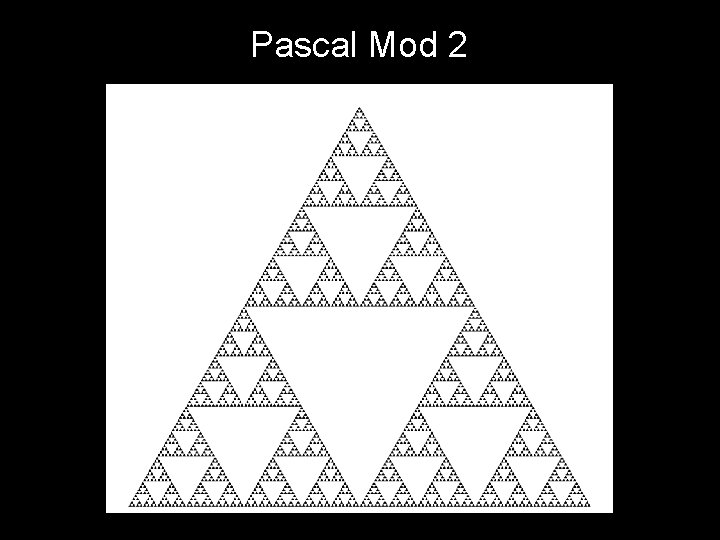
Pascal Mod 2

All these properties can be proved inductively and algebraically. We will give combinatorial proofs using the Manhattan block walking representation of binomial coefficients

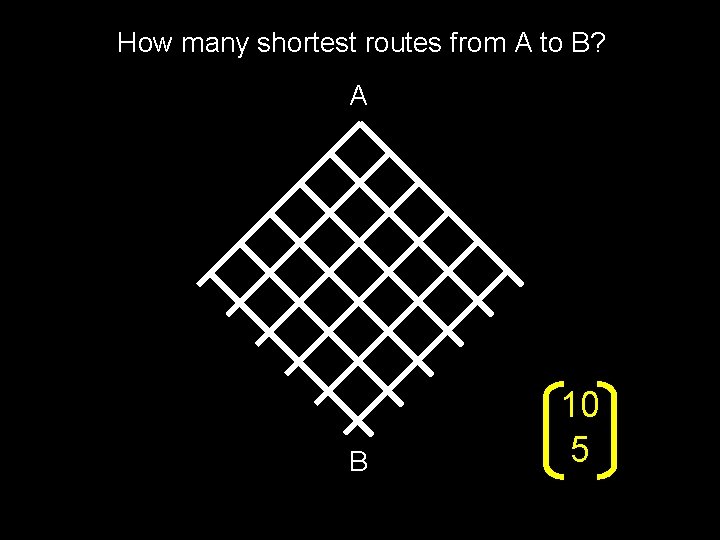
How many shortest routes from A to B? A B 10 5

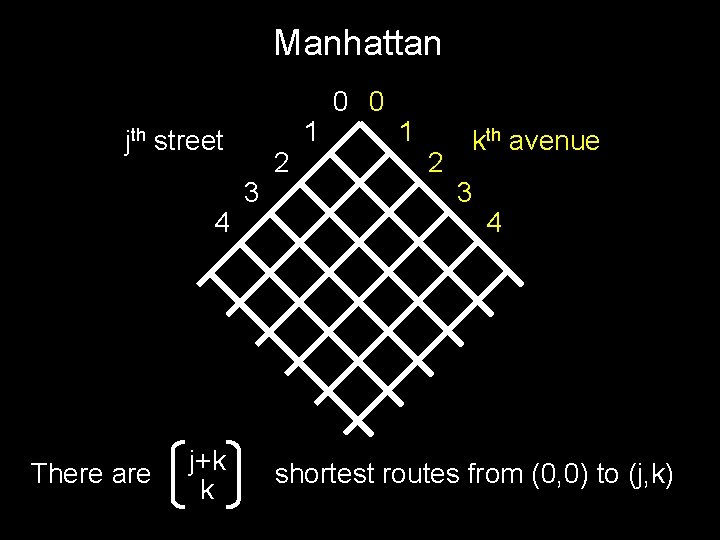
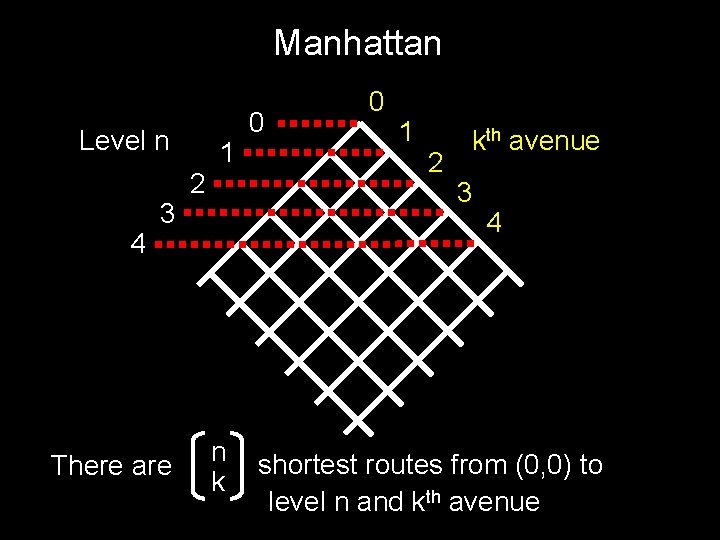
Manhattan jth street 4 There are j+k k 3 2 1 0 0 1 2 kth avenue 3 4 shortest routes from (0, 0) to (j, k)

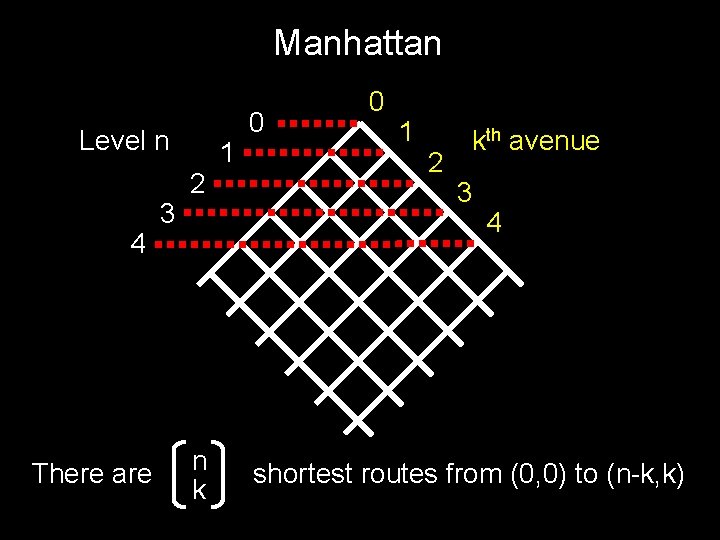
Manhattan Level n 4 There are 3 2 n k 1 0 0 1 2 kth avenue 3 4 shortest routes from (0, 0) to (n-k, k)

Manhattan Level n 4 3 There are 2 1 n k 0 0 1 2 kth avenue 3 4 shortest routes from (0, 0) to level n and kth avenue

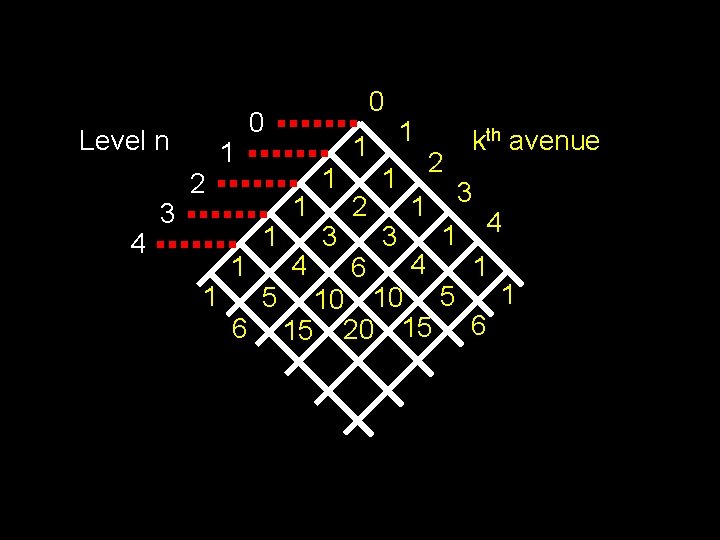
Level n 4 3 2 1 1 1 6 0 0 1 5 1 1 4 1 3 2 6 1 3 1 1 4 2 kth avenue 3 1 4 1 1 10 10 5 15 20 15 6

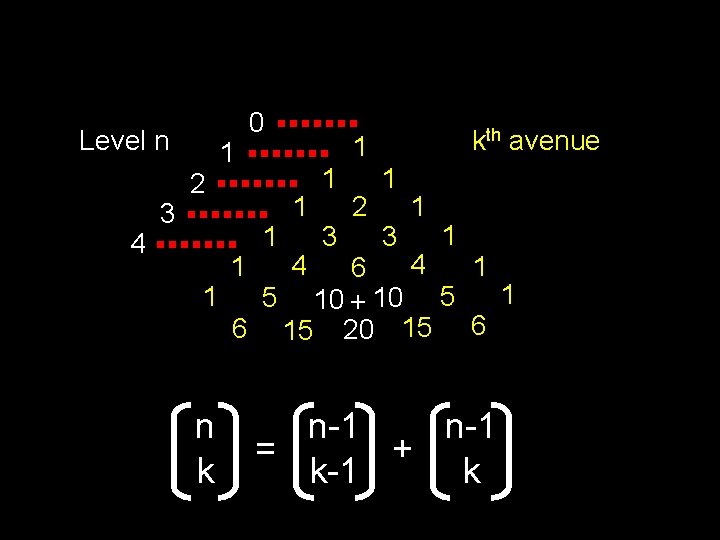
Level n 4 3 2 1 0 1 kth avenue 1 1 1 3 2 1 3 1 1 4 1 6 1 1 5 10 + 10 5 6 15 20 15 6 1 n k 4 n-1 = + k-1 k

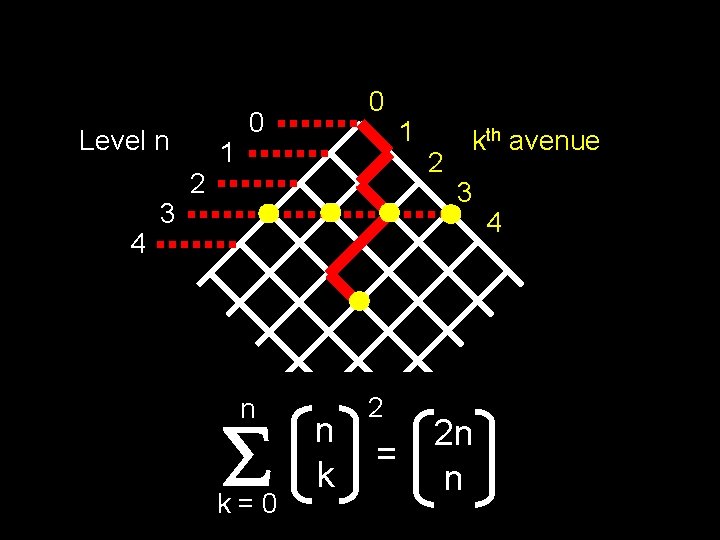
Level n 4 3 2 1 0 0 n k=0 n k 2 = 1 2 kth avenue 3 2 n n 4

Level n 4 3 2 1 0 0 n i=k i k 1 2 kth avenue 3 n+1 = k+1 4

Vector Programs Let’s define a (parallel) programming language called VECTOR that operates on possibly infinite vectors of numbers. Each variable V! can be thought of as: < * , * , *, *, … >

Vector Programs Let k stand for a scalar constant <k> will stand for the vector <k, 0, 0, 0, …> <0> = <0, 0, …> <1> = <1, 0, 0, 0, …> V! + T! means to add the vectors position-wise <4, 2, 3, …> + <5, 1, 1, …. > = <9, 3, 4, …>

Vector Programs RIGHT(V!) means to shift every number in V! one position to the right and to place a 0 in position 0 RIGHT( <1, 2, 3, …> ) = <0, 1, 2, 3, …>

Vector Programs Example: Store: V! : = <6>; V! : = RIGHT(V!) + <42>; V! : = RIGHT(V!) + <13>; V! = <6, 0, 0, 0, …> V! = <42, 6, 0, 0, …> V! = <2, 42, 6, 0, …> V!= <13, 2, 42, 6, …> V! = < 13, 2, 42, 6, 0, 0, 0, … >

Vector Programs Example: Store: V! : = <1>; V! = <1, 0, 0, 0, …> V! = <1, 1, 0, 0, …> V! = <1, 2, 1, 0, …> V!= <1, 3, 3, 1, …> Loop n times V! : = V! + RIGHT(V!); V! = nth row of Pascal’s triangle

1 X + 2 X + Vector programs can be implemented by polynomials! 3 X

Programs Polynomials The vector V! = < a 0, a 1, a 2, . . . > will be represented by the polynomial: PV = i=0 a i. X i

Formal Power Series The vector V! = < a 0, a 1, a 2, . . . > will be represented by the formal power series: PV = i=0 a i. X i

V ! = < a 0, a 1, a 2, . . . > PV = a i. X i i=0 <0> is represented by 0 <k> is represented by k V! + T! is represented by RIGHT(V!) is represented by (PV + PT) (PV X)

Vector Programs Example: V! : = <1>; PV : = 1; Loop n times V! : = V! + RIGHT(V!); PV : = PV + PV X; V! = nth row of Pascal’s triangle

Vector Programs Example: V! : = <1>; PV : = 1; Loop n times V! : = V! + RIGHT(V!); PV : = PV(1+X); V! = nth row of Pascal’s triangle

Vector Programs Example: V! : = <1>; Loop n times V! : = V! + RIGHT(V!); PV = (1+ X)n V! = nth row of Pascal’s triangle

• Polynomials count • Binomial formula • Combinatorial proofs of binomial identities • Vector programs Here’s What You Need to Know…
 Hhhhhhht
Hhhhhhht Compsci 230 review
Compsci 230 review Compsci 230 duke
Compsci 230 duke Compsci 230
Compsci 230 Solving recurrence relations
Solving recurrence relations Advanced counting
Advanced counting Basics of counting in discrete mathematics
Basics of counting in discrete mathematics Mathematics for computer science mit
Mathematics for computer science mit Die hard
Die hard Mathematics for computer science mit
Mathematics for computer science mit Rosen discrete mathematics solutions
Rosen discrete mathematics solutions Pigeonhole principle in discrete mathematics
Pigeonhole principle in discrete mathematics Mathematics 1
Mathematics 1 Logical form and logical equivalence
Logical form and logical equivalence Dfs in discrete mathematics
Dfs in discrete mathematics Find shortest path
Find shortest path Discrete mathematics sequences
Discrete mathematics sequences Tautological implications
Tautological implications Define antisymmetric relation
Define antisymmetric relation Application of propositional logic
Application of propositional logic Permutation and combination in discrete mathematics
Permutation and combination in discrete mathematics How to prove set identities
How to prove set identities Boolean function in discrete mathematics
Boolean function in discrete mathematics Discrete mathematics chapter 3 solutions
Discrete mathematics chapter 3 solutions Sets and functions in discrete mathematics
Sets and functions in discrete mathematics In triangle pqr
In triangle pqr Duality digital logic
Duality digital logic Incidence matrix in discrete mathematics
Incidence matrix in discrete mathematics Subtraction rule counting
Subtraction rule counting Travelling salesman problem discrete mathematics
Travelling salesman problem discrete mathematics What is discrete mathematics
What is discrete mathematics Pqqpq
Pqqpq Contoh soal kombinatorial
Contoh soal kombinatorial The domain of discrete numeric function is
The domain of discrete numeric function is What is recursion in discrete mathematics
What is recursion in discrete mathematics Declarative statement in discrete mathematics
Declarative statement in discrete mathematics M ary tree in discrete mathematics
M ary tree in discrete mathematics M ary tree in discrete mathematics
M ary tree in discrete mathematics Directed multigraph
Directed multigraph What is rooted tree in discrete mathematics
What is rooted tree in discrete mathematics Quantifiers discrete mathematics exercises
Quantifiers discrete mathematics exercises Discrete mathematics
Discrete mathematics Binary relations discrete math
Binary relations discrete math Ming-hsuan yang
Ming-hsuan yang Probability theory in discrete mathematics
Probability theory in discrete mathematics Binary relation in discrete mathematics
Binary relation in discrete mathematics Sets and propositions in discrete mathematics
Sets and propositions in discrete mathematics Implications math
Implications math Inverse relation discrete math
Inverse relation discrete math Induction and recursion discrete mathematics
Induction and recursion discrete mathematics Discrete mathematics chapter 1
Discrete mathematics chapter 1 Division algorithm discrete math
Division algorithm discrete math Recurrence relation in discrete mathematics
Recurrence relation in discrete mathematics Sandy irani discrete mathematics
Sandy irani discrete mathematics Discrete mathematics uses
Discrete mathematics uses Define antisymmetric relation
Define antisymmetric relation Discrete math
Discrete math A computer programming team has 13 members
A computer programming team has 13 members Sets and propositions
Sets and propositions What is a wff in logic
What is a wff in logic Floyd warshall algorithm path reconstruction
Floyd warshall algorithm path reconstruction Discrete math definition
Discrete math definition What is discrete mathematics
What is discrete mathematics Eular graph
Eular graph Discrete mathematics sandy irani pdf
Discrete mathematics sandy irani pdf























































































