Compressing Polygon Mesh Connectivity with Degree Duality Prediction

Overview • • Background Connectivity Compression Coding with Degrees Duality Prediction Adaptive Traversal Example

Polygon Meshes • connectivity face 1 1 2 3 4 face 2 3 4

Mesh Compression • Geometry Compression [Deering, 95] – Fast Rendering – Progressive Transmission –

Not Triangles … Polygons! Face Fixer [Isenburg & Snoeyink, 00]

Results model triceratops galleon cessna … tommygun cow teapot bits per vertex (bpv) Face

Connectivity Compression assumption • order of vertices does not matter advantage • no need

Connectivity Graphs • connectivity of simple meshes is homeomorphic to planar graph enumeration asymptotic

Spanning Tree • Succinct Representations of Graphs [Turan, 84] • Short encodings of planar

Region Growing • Triangle Mesh Compression [Touma & Gotsman, 98] • Cut-Border Machine [Gumhold

Classification • code symbols are associated with edges, faces, or vertices: boundary processed region

Edge-Based • Dual Graph Approach, [Lee & Kuo, 99] • Face Fixer, [Isenburg &

Edge-Based ? ? • Dual Graph Approach, [Lee & Kuo, 99] • Face Fixer,

Face-Based • Cut-Border Machine, [Gumhold & Strasser, 98] • Edgebreaker, [Rossignac, 99] processed region

Face-Based ? ? ? • Cut-Border Machine, [Gumhold & Strasser, 98] • Edgebreaker, [Rossignac,

Vertex-based • Triangle Mesh Compression, [Touma & Gotsman, 98] processed region unprocessed region focus

Vertex-based • Triangle Mesh Compression, [Touma & Gotsman, 98] processed region 5 unprocessed region

Vertex-based ? ? ? • Triangle Mesh Compression, [Touma & Gotsman, 98] processed region

Coding with Degrees while ( unprocessed faces ) move focus to a face degree

“add” free vertex boundary focus processed region exit focus end slotregion unprocessed 3 free

free vertex “splits” boundary unprocessed region S split offset processed region . . .

free vertex “merges” boundary in stack unprocessed region stack focus processed region M merge

Resulting Code • two symbol sequences – vertex degrees (+ “split” / “merge”). .

Entropy for a symbol sequence of t types Entropy = t i =1 1

Average Distributions add 4 4 3 split merge case 3 2 5 6 7

Adaptation to Regularity 6 . . . 3 . . . vertex degrees .

“Worst-case” Distribution 3 3 pi = 1 i =3 4 5 i • pi

Degree Correlation • high-degree faces are “likely” to be surrounded by low-degree vertices •

Face Degree Prediction fdc 3. 3 3 focus (widened) 4 3 average degree of

Vertex Degree Prediction 6 vdc = 3 vdc = 44 degree of focus face

Compression Gain model triceratops galleon cessna … tommygun cow teapot without bits per vertex

Occurance of “splits” unprocessed region

Occurance of “splits” unprocessed region split processed region

Adaptive Traversal • Valence-driven connectivity encoding for 3 D meshes [Alliez & Desbrun, 01]

Compression Gain model triceratops galleon cessna … tommygun cow teapot without splits bpv 53

Example Decoding Run 4 6 6 3 3 5 4 4 3 5 4

Example Decoding Run 4 4 6 6 3 3 5 4 4 3 5

Example Decoding Run focus 6 4 6 6 3 3 5 4 4 3

Example Decoding Run 3 free vertex 4 6 6 3 3 5 4 4

Example Decoding Run exit focus 6 4 6 6 3 3 5 4 4

Example Decoding Run free vertices 5 4 6 6 3 3 5 4 4

Example Decoding Run 3 4 6 6 3 3 5 4 4 3 4

Example Decoding Run 3 5 4 6 6 3 3 5 4 4 3

Example Decoding Run exit focus 4 4 6 6 3 3 5 4 4

Example Decoding Run 5 4 4 6 6 3 3 5 4 4 3

Example Decoding Run 4 exit focus 4 6 6 3 3 5 4 4

Example Decoding Run 5 end slot focus (widened) 3 3 start slot 4 6

Example Decoding Run exit focus 4 5 4 6 6 3 3 5 4

Example Decoding Run focus (widened) 4 6 6 3 3 5 4 4 3

Example Decoding Run 3 4 6 6 3 3 5 4 4 3 5

Example Decoding Run 6 4 6 6 3 3 5 4 4 3 5

Example Decoding Run 2 6 4 6 6 3 3 5 4 4 3

Example Decoding Run . . . 5 4 6 6 3 3 5 4

Summary • degree coding for polygonal connectivity • duality prediction • adaptive traversal •

Similar Result • Near-Optimal Connectivity Coding of 2 -manifold polygon meshes [Khodakovsky, Alliez, Desbrun,

Current Work (w. Pierre Alliez) • use polygons for better predictive geometry coding “fairly

Slides: 94

Download presentation

Compressing Polygon Mesh Connectivity with Degree Duality Prediction Martin Isenburg University of North Carolina at Chapel Hill

Overview • • Background Connectivity Compression Coding with Degrees Duality Prediction Adaptive Traversal Example Run Conclusion

Background

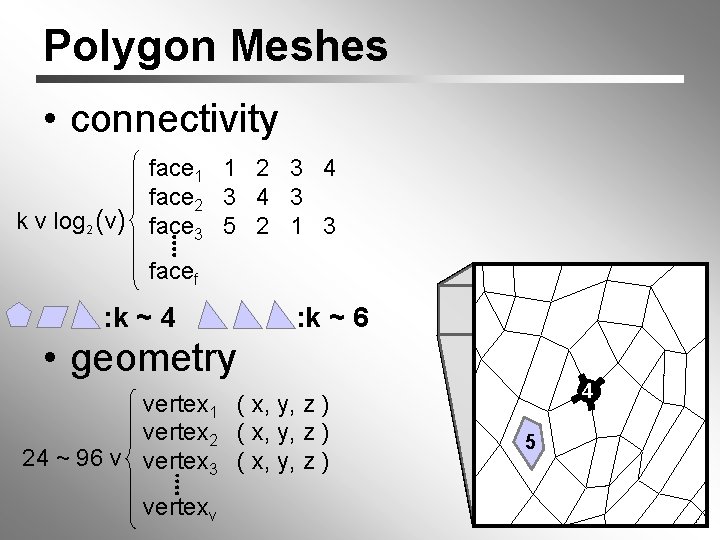
Polygon Meshes • connectivity face 1 1 2 3 4 face 2 3 4 3 k v log 2 (v) face 3 5 2 1 3 facef : k ~ 4 : k ~ 6 • geometry vertex 1 ( x, y, z ) vertex 2 ( x, y, z ) 24 ~ 96 v vertex 3 ( x, y, z ) vertexv 4 5

Mesh Compression • Geometry Compression [Deering, 95] – Fast Rendering – Progressive Transmission – Maximum. Compression • Geometry • Connectivity – Triangle Meshes – Polygon. Meshes

Not Triangles … Polygons! Face Fixer [Isenburg & Snoeyink, 00]

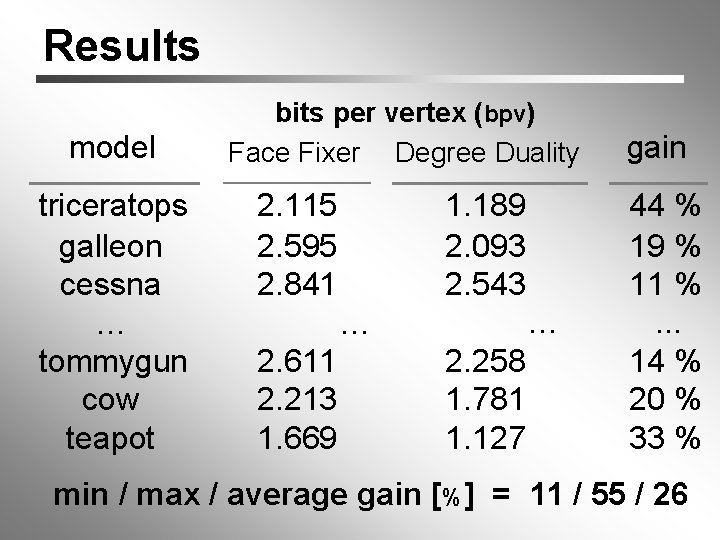
Results model triceratops galleon cessna … tommygun cow teapot bits per vertex (bpv) Face Fixer Degree Duality 1. 189 2. 093 2. 543 2. 115 2. 595 2. 841 … … 2. 611 2. 213 1. 669 2. 258 1. 781 1. 127 gain 44 % 19 % 11 %. . . 14 % 20 % 33 % min / max / average gain [%] = 11 / 55 / 26

Connectivity Compression

Connectivity Compression assumption • order of vertices does not matter advantage • no need to “preserve” indices approach • code only the “connectivity graph” • re-order vertices appropriately

Connectivity Graphs • connectivity of simple meshes is homeomorphic to planar graph enumeration asymptotic bounds [William Tutte 62 / 63] number of planar triangulations with v vertices 3. 24 bpv << 6 log (v) bpv 2

Spanning Tree • Succinct Representations of Graphs [Turan, 84] • Short encodings of planar graphs and maps [Keeler & Westbrook, 95] • Geometric Compression through Topological Surgery [Taubin & Rossignac, 98] extends to meshes of non-zero genus

Region Growing • Triangle Mesh Compression [Touma & Gotsman, 98] • Cut-Border Machine [Gumhold & Strasser, 98] • Edgebreaker [Rossignac, 99] • Simple Sequential Encoding [de Floriani et al. , 99] • Dual Graph Approach [Lee & Kuo, 99] • Face Fixer [Isenburg & Snoeyink, 00]

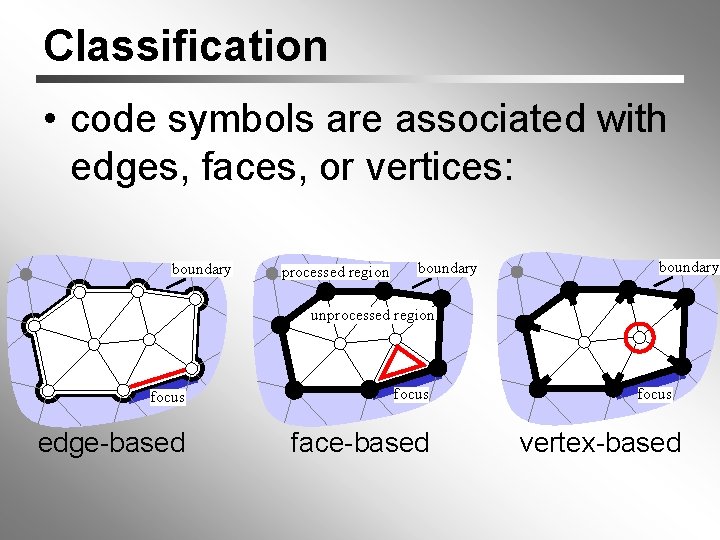
Classification • code symbols are associated with edges, faces, or vertices: boundary processed region boundary unprocessed region focus edge-based face-based focus vertex-based

Edge-Based Compression Schemes

Edge-Based • Dual Graph Approach, [Lee & Kuo, 99] • Face Fixer, [Isenburg & Snoeyink, 00] processed region unprocessed region focus . . . F F R

Edge-Based • Dual Graph Approach, [Lee & Kuo, 99] • Face Fixer, [Isenburg & Snoeyink, 00] processed region unprocessed region . . . F F R F F

Edge-Based • Dual Graph Approach, [Lee & Kuo, 99] • Face Fixer, [Isenburg & Snoeyink, 00] processed region unprocessed region . . . F F R

Edge-Based • Dual Graph Approach, [Lee & Kuo, 99] • Face Fixer, [Isenburg & Snoeyink, 00] processed region F unprocessed region . . . F F R F F F R

Edge-Based • Dual Graph Approach, [Lee & Kuo, 99] • Face Fixer, [Isenburg & Snoeyink, 00] processed region R F unprocessed region . . . F F R F R F F R

Edge-Based ? ? • Dual Graph Approach, [Lee & Kuo, 99] • Face Fixer, [Isenburg & Snoeyink, 00] processed region R F F unprocessed region F R F . . . F F R F R F. . . 5 4 3 6 4. . . ?

Face-Based Compression Schemes

Face-Based • Cut-Border Machine, [Gumhold & Strasser, 98] • Edgebreaker, [Rossignac, 99] processed region unprocessed region focus . . . C R

Face-Based • Cut-Border Machine, [Gumhold & Strasser, 98] • Edgebreaker, [Rossignac, 99] processed region unprocessed region . . . C R C C

Face-Based • Cut-Border Machine, [Gumhold & Strasser, 98] • Edgebreaker, [Rossignac, 99] processed region R unprocessed region . . . C R C

Face-Based • Cut-Border Machine, [Gumhold & Strasser, 98] • Edgebreaker, [Rossignac, 99] processed region R R unprocessed region . . . C R R C

Face-Based ? ? ? • Cut-Border Machine, [Gumhold & Strasser, 98] • Edgebreaker, [Rossignac, 99] processed region C unprocessed region . . . C R R C. . . 5 4 3 6 4. . . R R C

Vertex-Based Compression Schemes

Vertex-based • Triangle Mesh Compression, [Touma & Gotsman, 98] processed region unprocessed region focus . . . 6

Vertex-based • Triangle Mesh Compression, [Touma & Gotsman, 98] processed region 5 unprocessed region . . . 6 5

Vertex-based ? ? ? • Triangle Mesh Compression, [Touma & Gotsman, 98] processed region 6 unprocessed region . . . 6. . . 5 6 5 4 3 6 . . . 4. . . 5

Coding with Vertex and Face Degrees

Coding with Degrees while ( unprocessed faces ) move focus to a face degree for ( free vertices ) case switch ( case ) “add”: vertex degree “split”: offset “merge”: index,

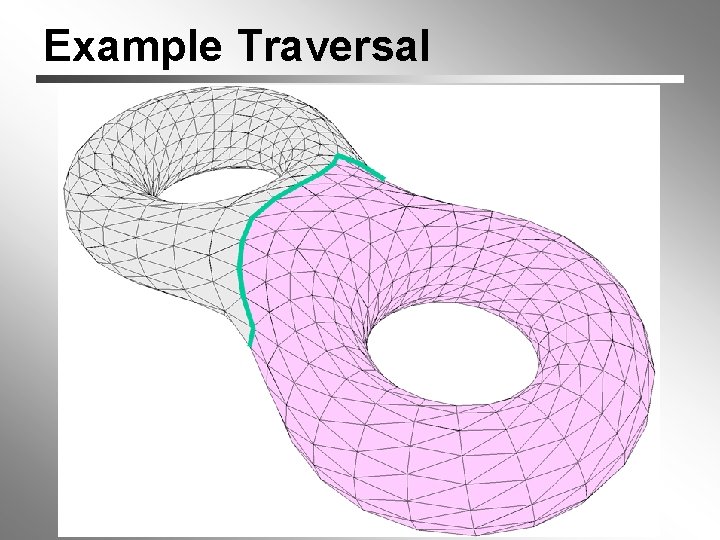
Example Traversal

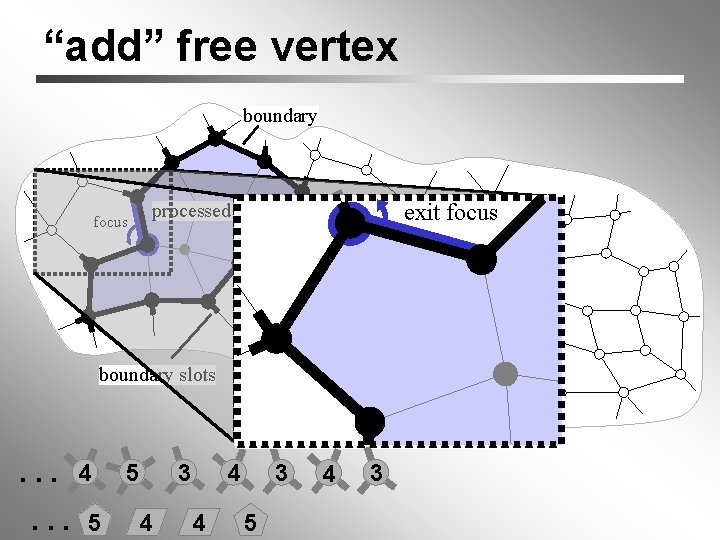
“add” free vertex boundary focus processed region exit focus end slotregion unprocessed 3 free vertices 5 focus (widened) 4 boundary slots start slot . . . 4. . . 5 5 3 4 4 4 3 5 4 3

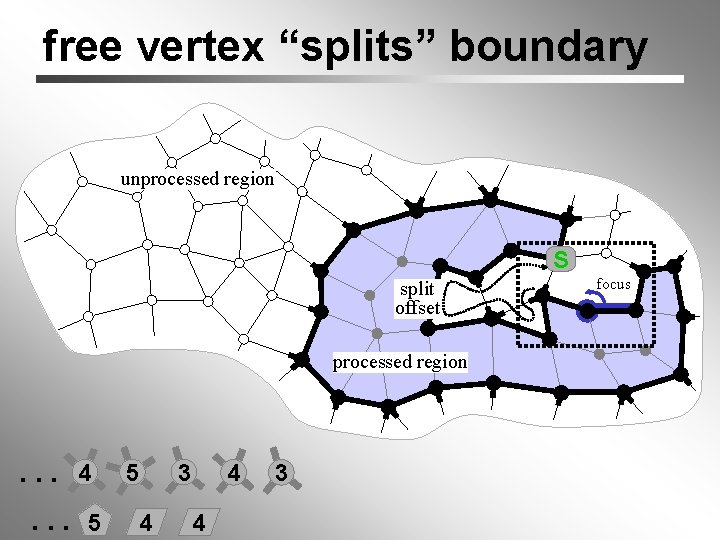
free vertex “splits” boundary unprocessed region S split offset processed region . . . 4. . . 5 5 3 4 4 4 3 focus

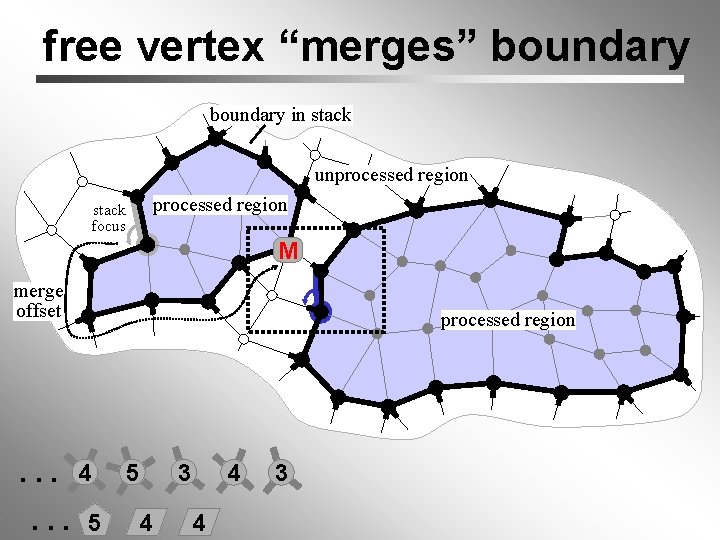
free vertex “merges” boundary in stack unprocessed region stack focus processed region M merge offset . . . 4. . . 5 processed region 5 3 4 4 4 3

Resulting Code • two symbol sequences – vertex degrees (+ “split” / “merge”). . . 4 3 S 4 4 M 6 4 5 4 4. . . – face degrees. . . 4 3 4 4 5 4 4 4 6 4 4 4. . . • compress with arithmetic coder converges to entropy

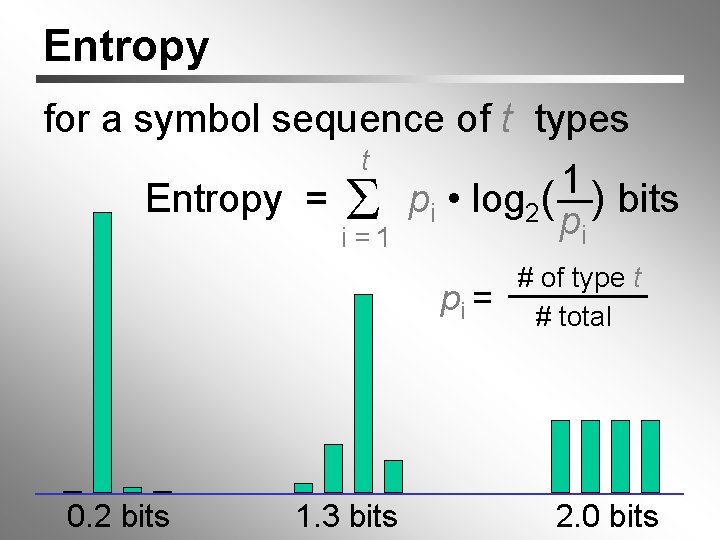
Entropy for a symbol sequence of t types Entropy = t i =1 1 pi • log 2( ) bits pi pi = 0. 2 bits 1. 3 bits # of type t # total 2. 0 bits

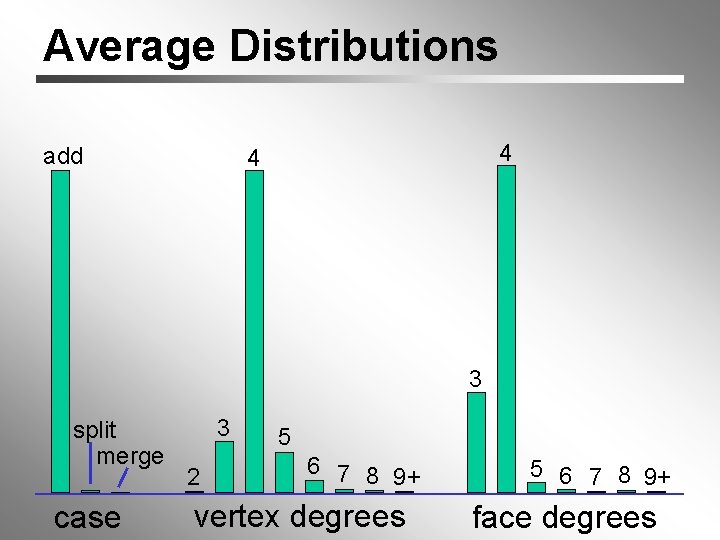
Average Distributions add 4 4 3 split merge case 3 2 5 6 7 8 9+ vertex degrees 5 6 7 8 9+ face degrees

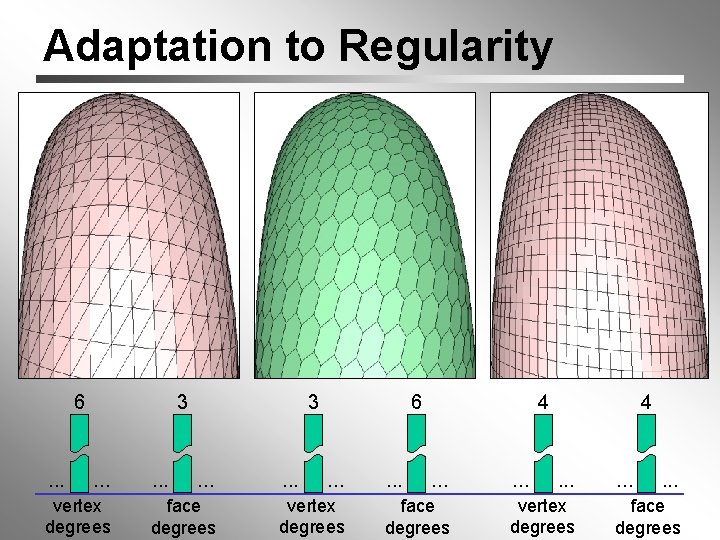
Adaptation to Regularity 6 . . . 3 . . . vertex degrees . . . 3 . . . face degrees . . . 6 . . . vertex degrees . . . 4 . . . face degrees . . . 4 . . . vertex degrees . . . face degrees

“Worst-case” Distribution 3 3 pi = 1 i =3 4 5 i • pi = 6 6 [Alliez & Desbrun, 01] 3. 241… bpv [Tutte, 62] i =3 7 8 9 …… … vertex degrees face degrees

Compressing with Duality Prediction

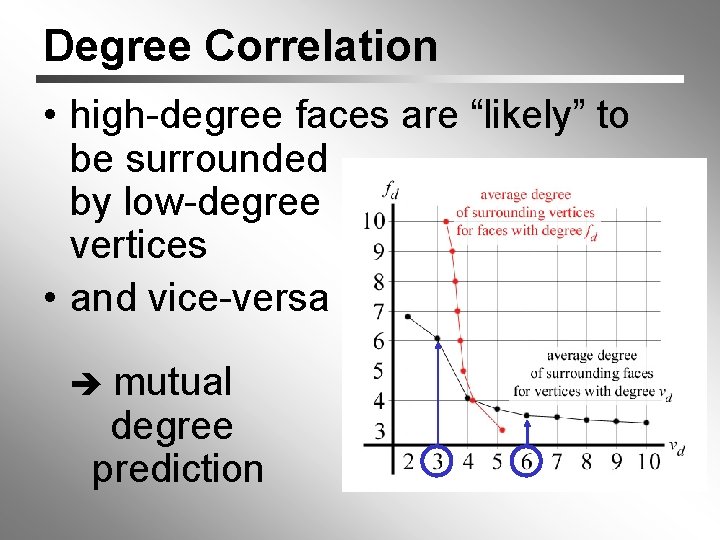
Degree Correlation • high-degree faces are “likely” to be surrounded by low-degree vertices • and vice-versa mutual degree prediction

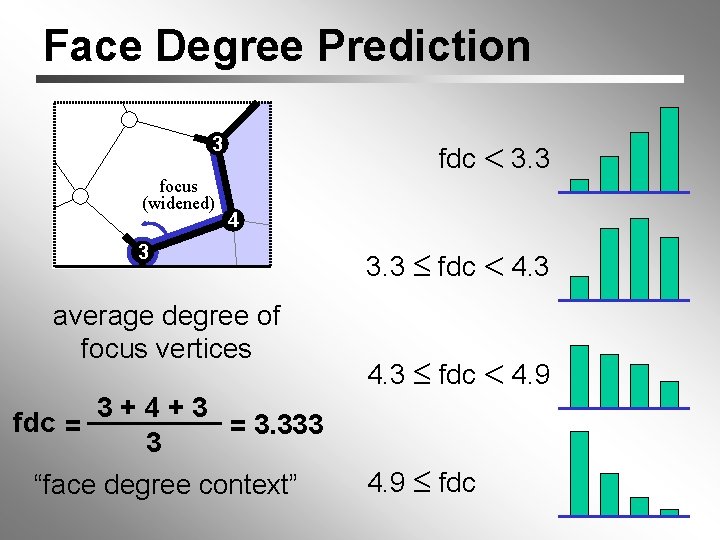
Face Degree Prediction fdc 3. 3 3 focus (widened) 4 3 average degree of focus vertices 3+4+3 fdc = = 3. 333 3 “face degree context” 3. 3 fdc 4. 9 fdc

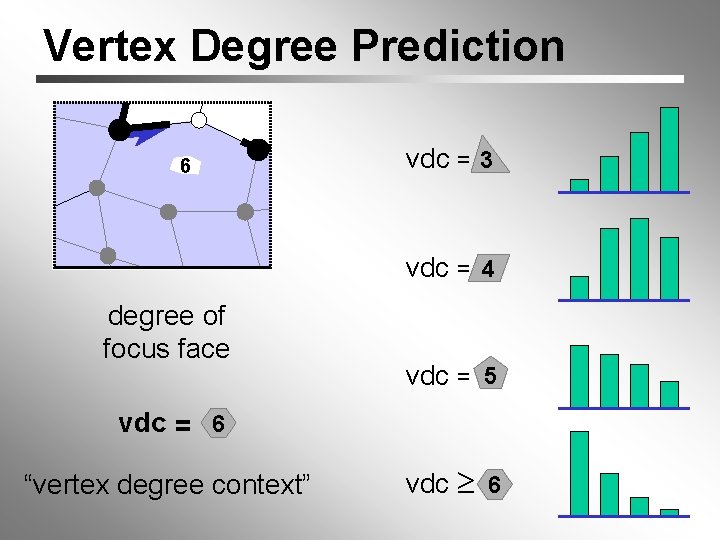
Vertex Degree Prediction 6 vdc = 3 vdc = 44 degree of focus face vdc = 55 vdc = 6 “vertex degree context” vdc 66

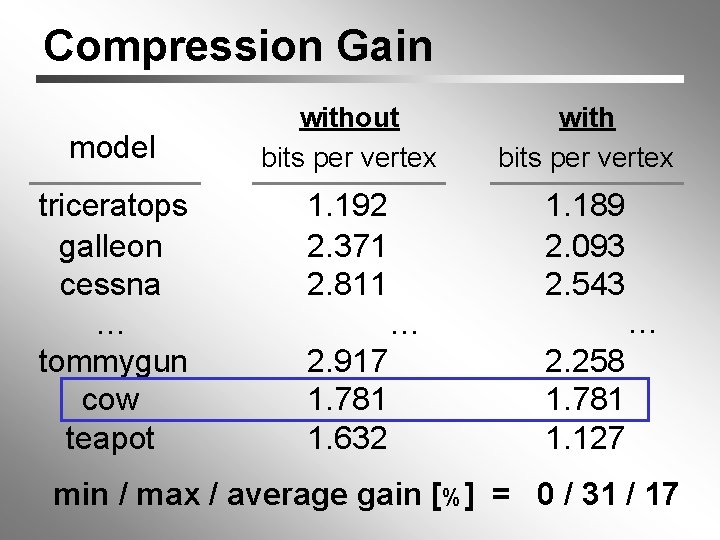
Compression Gain model triceratops galleon cessna … tommygun cow teapot without bits per vertex with bits per vertex 1. 192 2. 371 2. 811 1. 189 2. 093 2. 543 … … 2. 917 1. 781 1. 632 2. 258 1. 781 1. 127 min / max / average gain [%] = 0 / 31 / 17

Reducing the Number of Splits

Occurance of “splits”

Occurance of “splits” unprocessed region

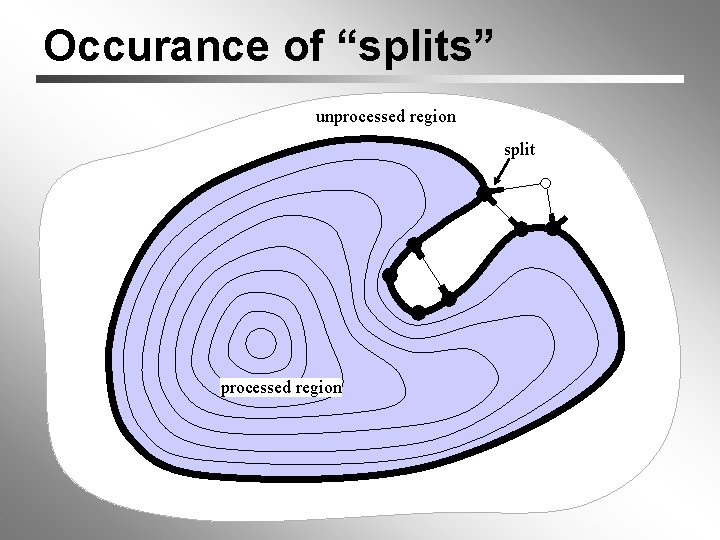
Occurance of “splits” unprocessed region split processed region

Adaptive Traversal • Valence-driven connectivity encoding for 3 D meshes [Alliez & Desbrun, 01] avoid creation of cavities exit focus

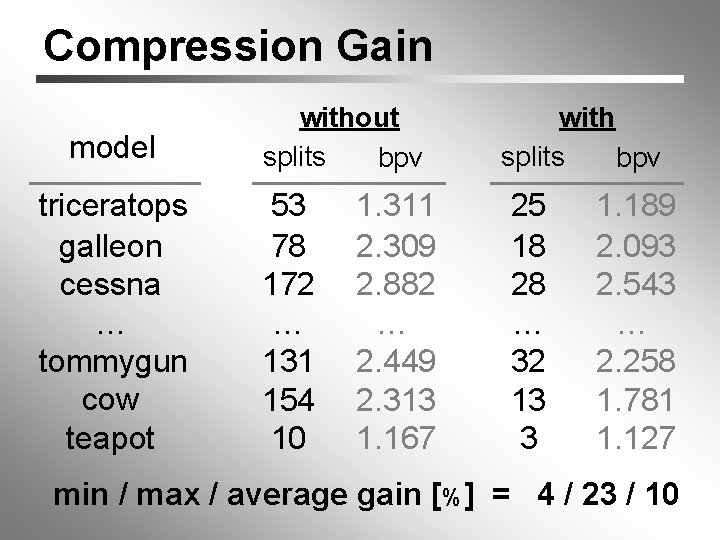
Compression Gain model triceratops galleon cessna … tommygun cow teapot without splits bpv 53 78 172 … 131 154 10 1. 311 2. 309 2. 882 … 2. 449 2. 313 1. 167 with splits bpv 25 18 28 … 32 13 3 1. 189 2. 093 2. 543 … 2. 258 1. 781 1. 127 min / max / average gain [%] = 4 / 23 / 10

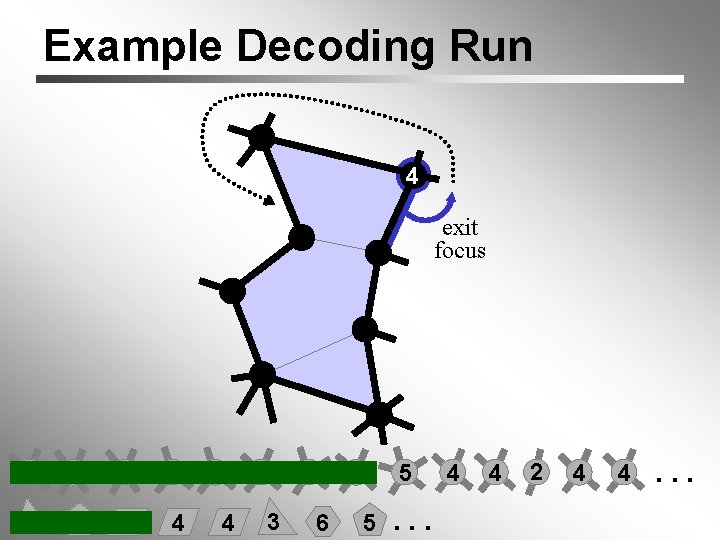
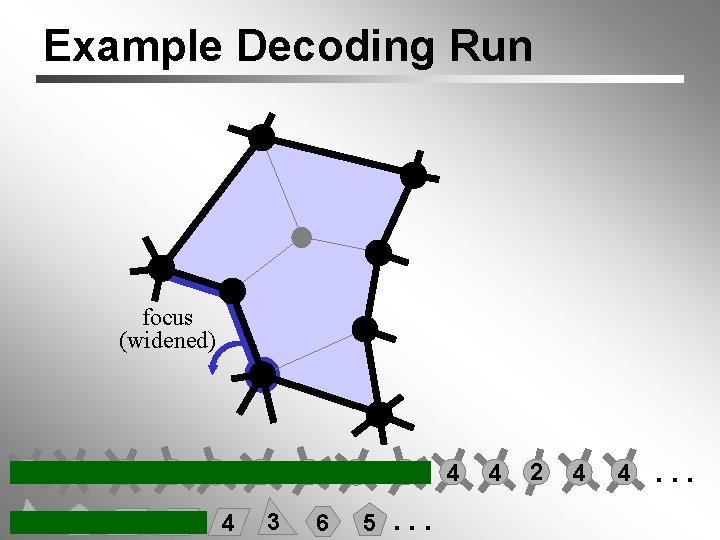
Example Decoding Run

Example Decoding Run 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

Example Decoding Run 4 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

Example Decoding Run focus 6 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

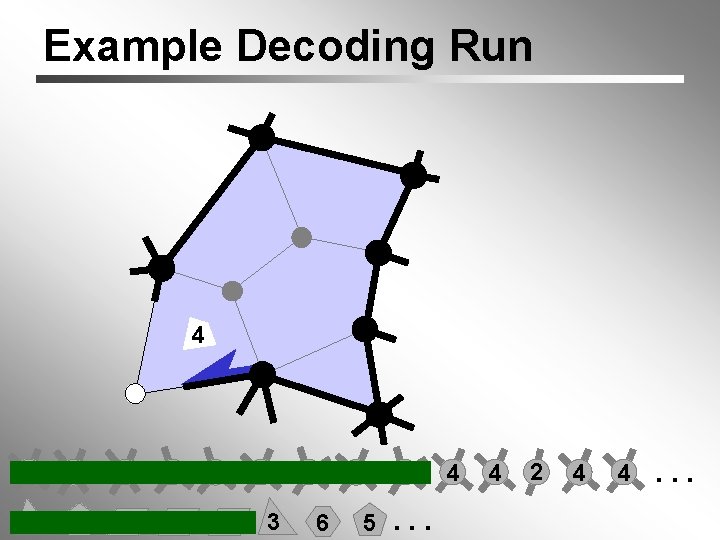
Example Decoding Run 3 free vertex 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

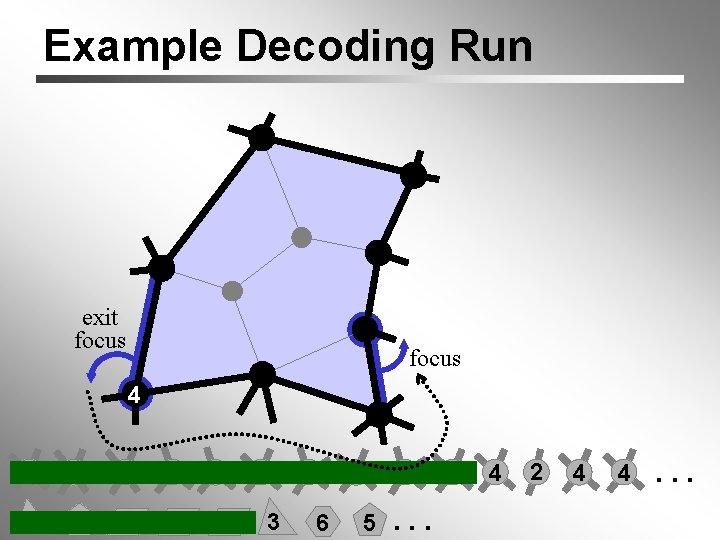
Example Decoding Run exit focus 6 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

Example Decoding Run free vertices 5 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

Example Decoding Run 3 4 6 6 3 3 5 4 4 3 4 5 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

Example Decoding Run 3 5 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

Example Decoding Run exit focus 4 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

Example Decoding Run 4 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

Example Decoding Run 5 4 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

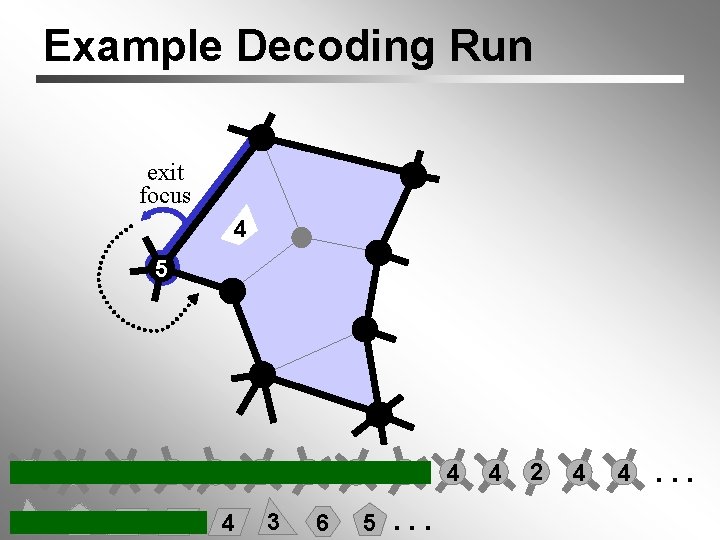
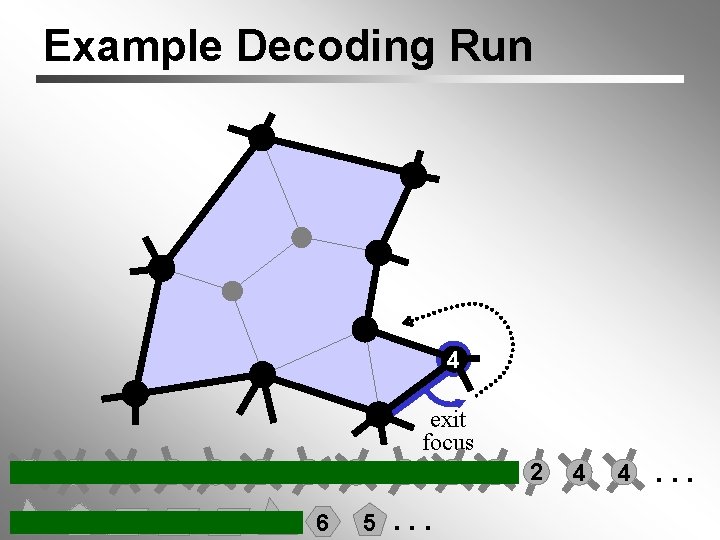
Example Decoding Run 4 exit focus 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

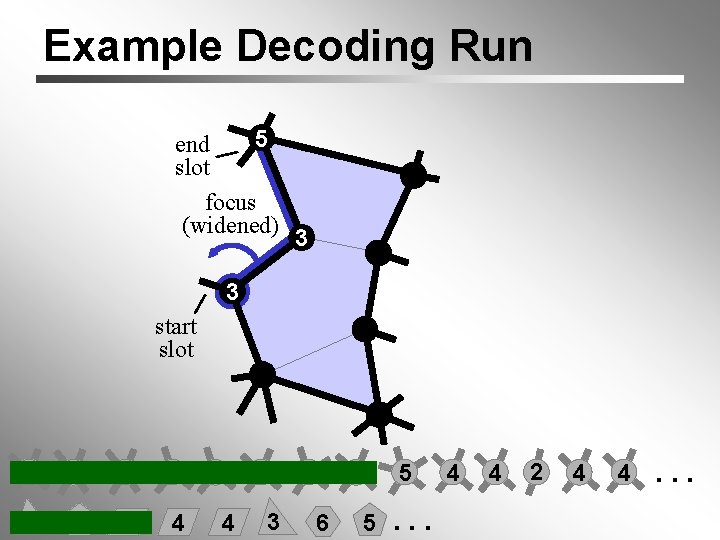
Example Decoding Run 5 end slot focus (widened) 3 3 start slot 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

Example Decoding Run 4 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

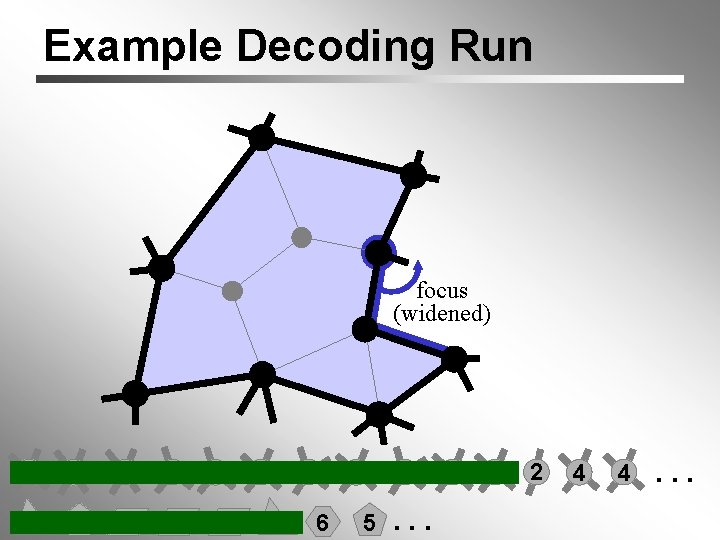
Example Decoding Run exit focus 4 5 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

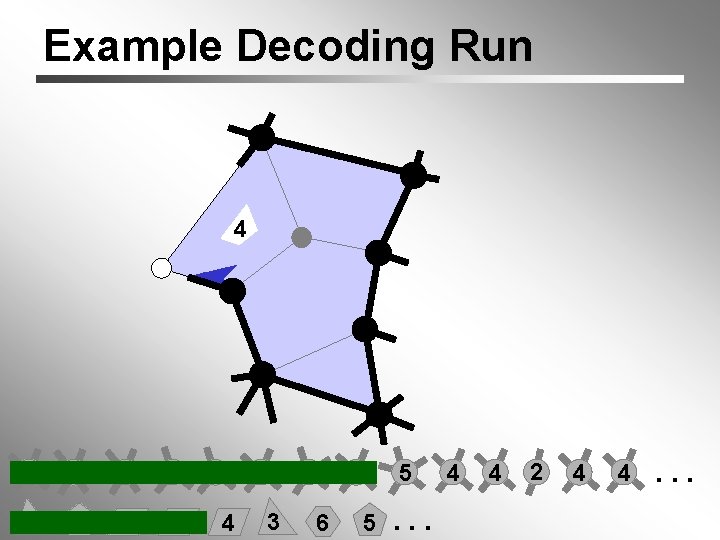
Example Decoding Run focus (widened) 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

Example Decoding Run 4 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

Example Decoding Run exit focus 4 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

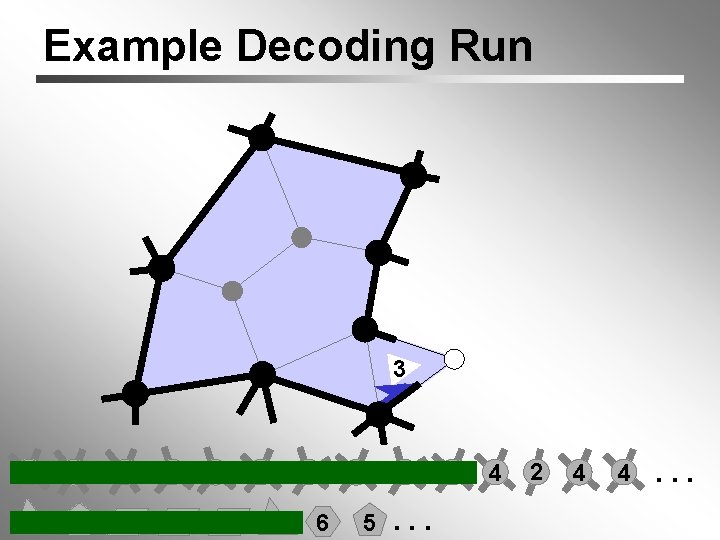
Example Decoding Run 3 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

Example Decoding Run 4 4 6 6 3 3 5 4 4 3 5 4 6 exit focus 5 4 4 5. . . 2 4 4. . .

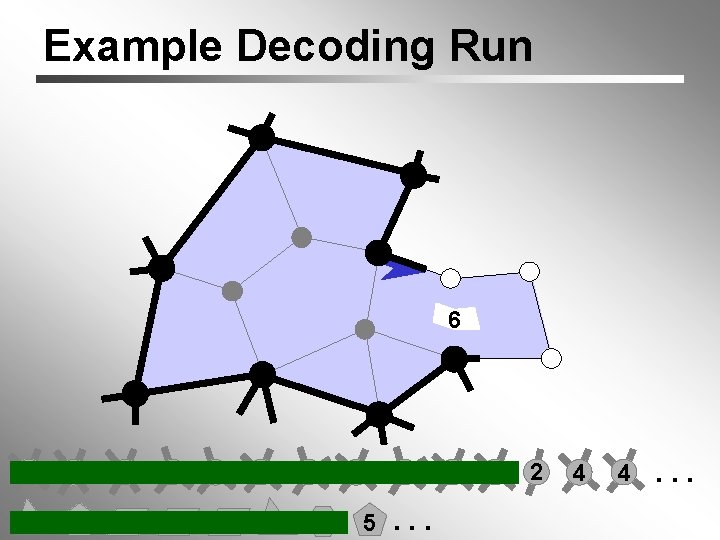
Example Decoding Run focus (widened) 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

Example Decoding Run 6 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

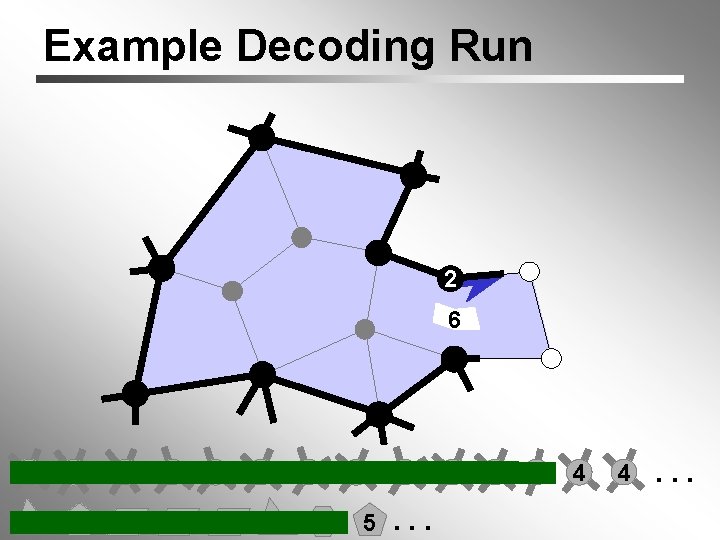
Example Decoding Run 2 6 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

Example Decoding Run 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

Example Decoding Run 4 exit focus 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

Example Decoding Run focus (widened) 4 6 6 3 3 5 4 4 3 5 4 6 5 5. . . 4 4 2 4 4. . .

Example Decoding Run . . . 5 4 6 6 3 3 5 4 4 3 5 4 6 5 5 . . . 4 4 2 4 4. . .

Conclusion

Summary • degree coding for polygonal connectivity • duality prediction • adaptive traversal • proof-of-concept implementation using Shout 3 D http: //www. cs. unc. edu/~isenburg/degreedualitycoder/

Similar Result • Near-Optimal Connectivity Coding of 2 -manifold polygon meshes [Khodakovsky, Alliez, Desbrun, Schröder] analysis of worst-case face degree and vertex degree distribution entropy Tutte’s bounds Martin France

Current Work (w. Pierre Alliez) • use polygons for better predictive geometry coding “fairly planar & convex” • extend degree coding to volume mesh connectivity “edge degrees”

Thank You!