Compound Probability Compound events Finding the probability of

Compound Probability Compound events: Finding the probability of two or more events. Key word: AND Two die are thrown. What is the probability of throwing a 4 on the first die AND a 3 on the second die?

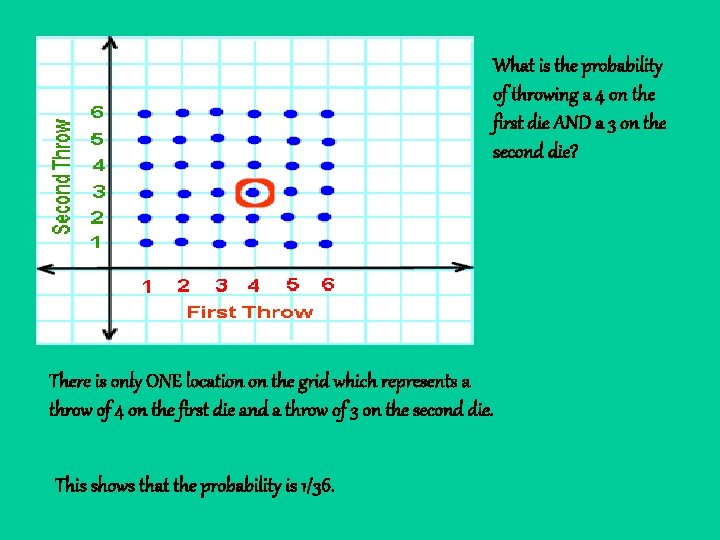
What is the probability of throwing a 4 on the first die AND a 3 on the second die? There is only ONE location on the grid which represents a throw of 4 on the first die and a throw of 3 on the second die. This shows that the probability is 1/36.

Probability of AND events: Notation: P(A and B) = P(A) • P(B) Probability of AND events, you MULTIPLY! If you draw a card from a deck numbers 1 through 10 and toss a die, find the probability of each outcome. Event B: roll a die Event A: pick a card Outcomes when you roll a die: Outcomes when you pick a card: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 1, 2, 3, 4, 5, 6

If you draw a card from a deck numbers 1 through 10 and toss a die, find the probability of each outcome. Event A: pick a card Outcomes: 10 1. P(a 10 and a 3) P(10) = _1_ P(3) = _1_ 10 6 Event B: roll a die Outcomes: 6 2. two even numbers P(even) = _5_ = _1_ P(even) = _1_ 10 2 2 P(10 and 3)= P(2 even)= _1_ • _1_ = _1_ 10 6 60 _1_ • _1_ = _1_ 2 2 4

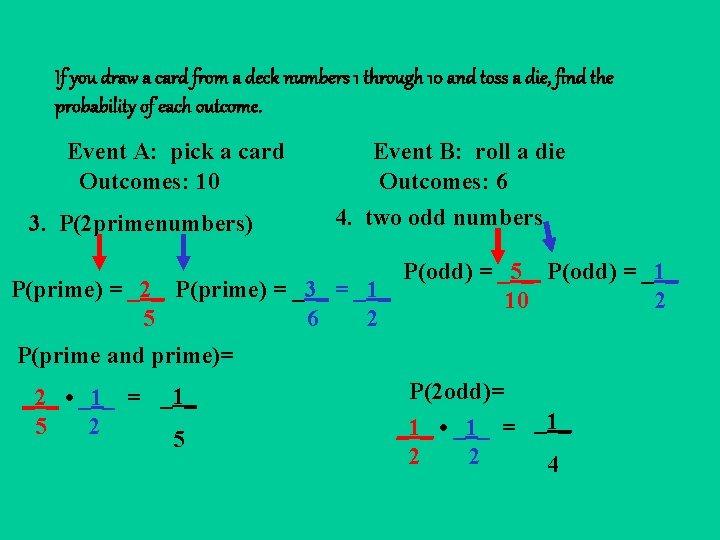
If you draw a card from a deck numbers 1 through 10 and toss a die, find the probability of each outcome. Event A: pick a card Outcomes: 10 3. P(2 primenumbers) Event B: roll a die Outcomes: 6 4. two odd numbers P(odd) = _5_ P(odd) = _1_ P(prime) = _2_ P(prime) = _3_ = _1_ 10 2 5 6 2 P(prime and prime)= _2_ • _1_ = _1_ 5 2 5 P(2 odd)= _1_ • _1_ = _1_ 2 2 4

If you draw a card from a deck numbers 1 through 10 and toss a die, find the probability of each outcome. Event A: pick a card Outcomes: 10 Event B: roll a die Outcomes: 6 5. P(even and prime) P(even) = _1_ 2 P(prime) = _3_ = _1_ 6 2 P(prime and prime)= _1_ • _1_ = _1_ 2 2 4

There are 4 red pencils, 6 green pencils, and 5 yellow pencils in a jar. Once a pencil is selected, it is not replaced. Find the probability of each outcome. Event A: pick a pencil Event B: pick a pencil Outcomes: 15 Outcomes: 14 7. two green 6. P(red and yellow) P(r) = _4_ 15 P(y) = _5_ 14 P(green) = _6_ 15 P(red and yellow)= P(2 green)= _4_ • _5_ = _20_ = 2_ 15 14 210 21 _6_ • 15 P(green) = _5_ 14 _5_ = _30_ = _1_ 14 210 7

There are 4 red pencils, 6 green pencils, and 5 yellow pencils in a jar. Once a pencil is selected, it is not replaced. Find the probability of each outcome. Event A: pick a pencil Event B: pick a pencil Outcomes: 15 Outcomes: 14 8. P(green and yellow) P(r) = _6_ 15 P(y) = _5_ 14 P(green and yellow)= _6_ • _5_ = _30_ = 1_ 15 14 210 7