Compound Matrices in Systems and Control Theory and

Compound Matrices in Systems and Control: Theory and Applications Michael Margaliot Joint work with: Eyal Weiss, Yoram Zarai, Chengshuai Wu, Raz Pines, Eduardo D. Sontag, and Jean-Jacques Slotine. 1

1. Honest disclosure 2. Questions welcome anytime 2

Let Outline Fix Applications to non-linear time-varying dynamical systems: k-positive and k-cooperative systems totally positive differential systems k-order contractive systems in the Hausdorff dimension 3

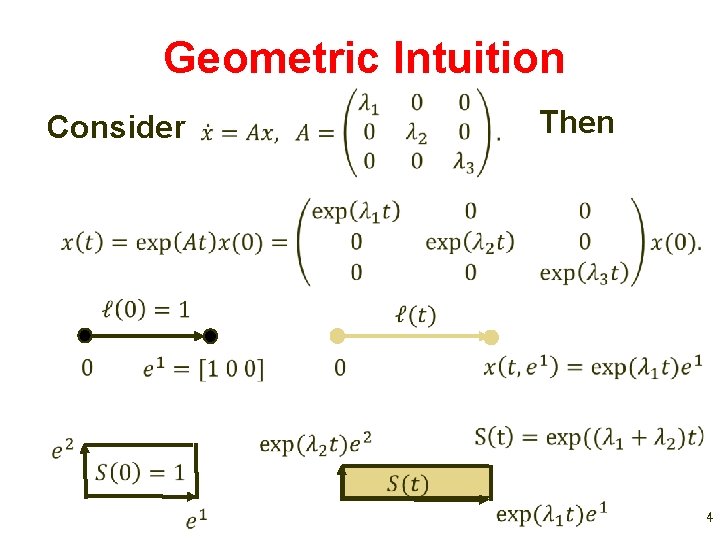
Geometric Intuition Consider Then 4

Geometric Intuition Consider Then Lengths evolve with rates Areas evolve with rates Volumes evolve with rates 5

Geometric Intuition 6

Minors of a Matrix Consider has Fix k-order minors. 1 -order minors = the entries of A n-order minor = det(A) 7

k-order Multiplicative Compound (MC) Let Def. The k-order MC of denoted is the matrix that contains all the minors of A (in lexicographical order). 8

k-order MC of a Diagonal Matrix Suppose that 9

Properties of the k-order Multiplicative Compound Theorem 1 Let The eigenvalues of products of the with eigenvalues are all the k Theorem 2 (Cauchy–Binet) Let Then This justifies the term multiplicative compound (MC). Example: 10

k-order Additive Compound Def. The k-order additive compound of A is In other words, The eigenvalues of are: 11

k-order MC in Dynamical Systems Consider Then evolution of lines evolution of 2 D bodies evolution of 3 D bodies evolution of n. D bodies 13

k-order MC and AC in Dynamical Systems Consider Let Then 14

k-order MC and AC in Dynamical Systems Consider Let “Compound matrices and ordinary differential equations”, Muldowney, Rocky Mountain J. Math. , 1990. 15

MC and AC in Systems and Control: Basic Idea via Three Examples Example 1 A is called diagonally stable if there exists a diagonal such that “Diagonal stability of a class of cyclic systems and its connection with the secant criterion”, Arcak & Sontag, Automatica, 2006. 16

MC and AC in Systems and Control: Basic Idea via Three Examples Example 1 A is called diagonally stable if there exists a diagonal such that Question: W������� ���� 17

MC and AC in Systems and Control: Basic Idea via Three Examples Such a system is called a positive system. Rantzer & Valcher, “Scalable control of positive systems”, 2021. Question: W������� ���� Metzler 18

MC and AC in Systems and Control: Basic Idea via Three Examples 19

MC and AC in Systems and Control: Basic Idea via Three Examples --”Diagonal Stability of discrete-time k-positive linear systems with applications to nonlinear systems”, Wu and Margaliot, submitted. --”Revisiting totally positive differential systems: A tutorial and new results”, Margaliot and Sontag, Automatica, 2019. --”A generalization of linear positive systems with applications to nonlinear systems: Invariant sets and the Poincaré–Bendixson property”, Weiss and Margaliot, Automatica, 2021. 20

MC and AC in Systems and Control: Basic Idea via Three Examples --”k-Order Contraction: Theory and Applications”, Wu, Kanevskiy, and Margaliot, submitted. --”A generalization of the multiplicative and additive compounds of square matrices and contraction in the Hausdorff dimension”, Wu, Pines, Margaliot and Slotine, submitted. 21

From Positive Systems to k-positive Systems Number of sign variations in a vector Linear maps that preserve the number of sign variations in a vector 22

Sign Variations in a Vector For a vector with no zero entries, the number of sign variations is: 23

Linear Mapping that Preserve Thm. If is totally non-negative then for all see Oscillation Matrices and Small Vibrations of Mechanical Systems, Krein & Gantmacher. Thm. If all k-order minors of non-negative then are “A generalization of linear positive systems with applications to nonlinear systems: Invariant sets and the Poincaré–Bendixson property”, Weiss and Margaliot, Automatica, 2021. 24

k-positive Systems A matrix is called Metzler if its off-diagonal entries are non-negative. The system is called positive if is Metzler for all Def. The system is called k-positive if is Metzler for all 25

k-positive Systems Def. The system is k-positive if is Metzler for all Let 26

k-positive Systems Let Thm. If is k-positive then for all The flow of k-positive systems maps the set of vectors with up to (k-1) sign variations to itself. For k=1, this recovers positive systems. 27

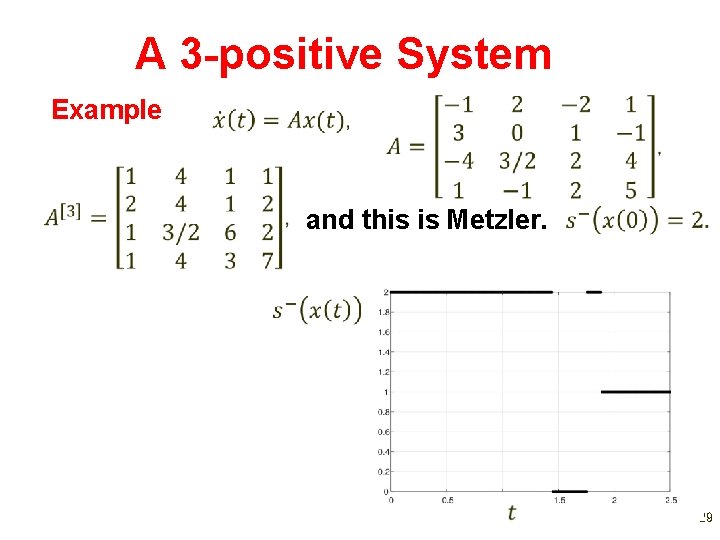
k-positive Systems Thm. If is k-positive then for all Example Here, and this is Metzler. The system is 3 -positive. Take: 28

A 3 -positive System Example and this is Metzler. 29

k-positive Systems and Nonlinear Systems Consider Let Thm. (Hirsch, 1988) Almost every bounded trajectory converges to an equilibrium. Thm. (Weiss & Margaliot, 2021) If the nonlinear system is 2 -cooperative then it satisfies the Poincaré-Bendixson property. 30

k-order Contraction Fix The induced matrix norm is The induced matrix measure is Consider so and thus 31

k-order Contraction Consider Let Denote Then and the variational equation 32

k-order Contraction Consider Denote Let Thus, describes the evolution of k-dim. bodies along the variational equation, and 33

k-order Contraction Consider Denote Let Then describes the evolution of k-dim. bodies along the variational equation, and J. S. Muldowney. "Compound Matrices and Ordinary Differential Equations", The Rocky Mountain J. Math. , 1990. 34

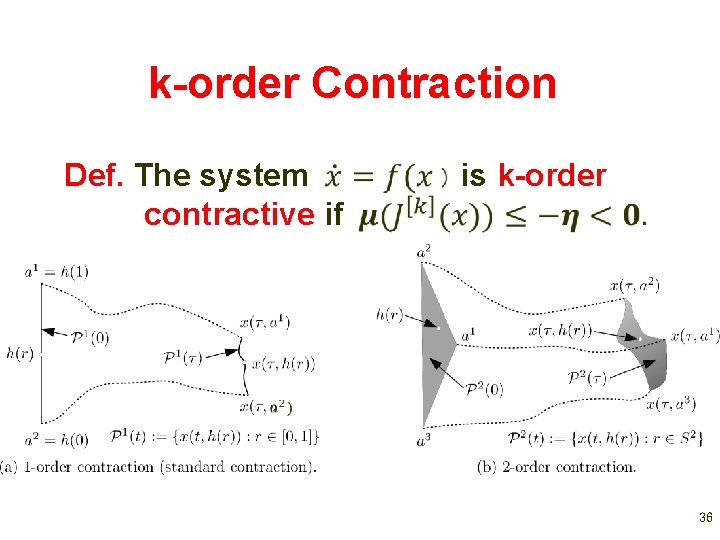
k-order Contraction Consider Denote Let Then describes the evolution of k-dim. bodies along the variational equation, and Def. The system contractive if is k-order 35

k-order Contraction Def. The system contractive if is k-order For this reduces to standard contractive systems. 36

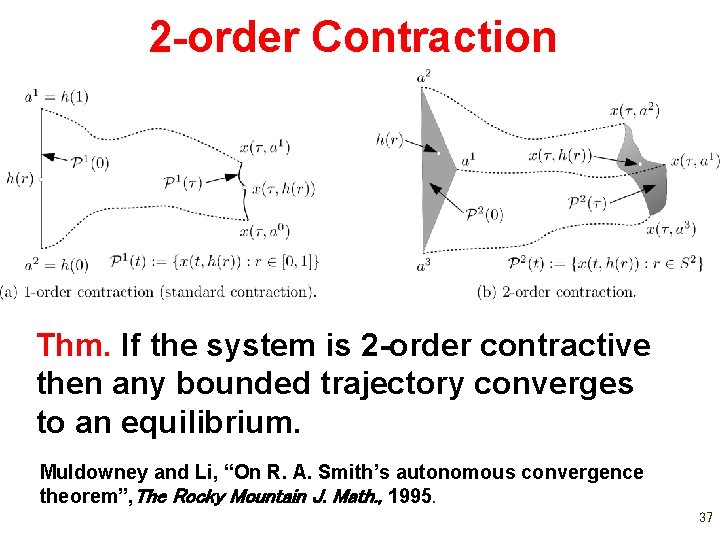
2 -order Contraction Thm. If the system is 2 -order contractive then any bounded trajectory converges to an equilibrium. Muldowney and Li, “On R. A. Smith’s autonomous convergence theorem”, The Rocky Mountain J. Math. , 1995. 37

-order Contraction Can we define What will it mean if Def. Fix Let For example, --”A generalization of the multiplicative and additive compounds of square matrices and contraction in the Hausdorff dimension”, Wu, Pines, Margaliot and Slotine, submitted. 38

-order Contraction Def. Fix Let Def. The system contractive if is –order --”A generalization of the multiplicative and additive compounds of square matrices and contraction in the Hausdorff dimension”, Wu, Pines, Margaliot and Slotine, submitted. 39

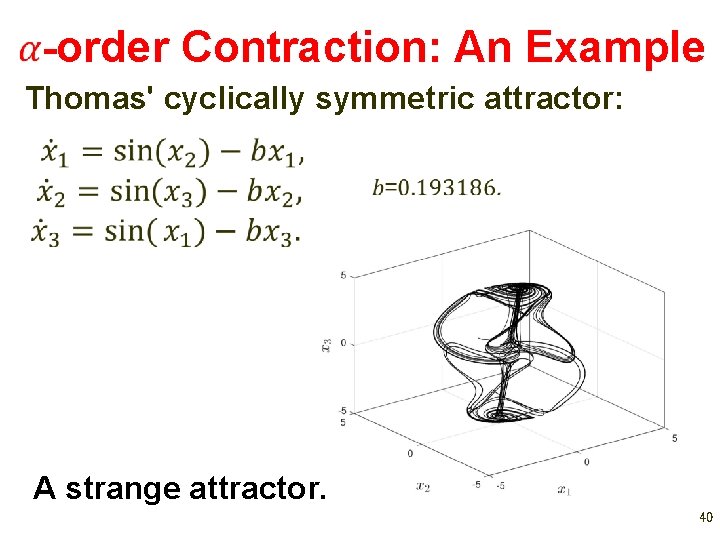
-order Contraction: An Example Thomas' cyclically symmetric attractor: A strange attractor. 40

-order Contraction: An Example Thomas' cyclically symmetric attractor: 41

-order Contraction: An Example Thomas' cyclically symmetric attractor: The system is 2+s contractive for s>0. 51427742

-order Contraction: An Example Thomas' cyclically symmetric attractor: The closed-loop system is 2 -order contractive when 43

Conclusion Compound matrices play an important role in geometry and multi-linear algebra. They also have an important and intuitive meaning in systems and control theory. In particular, we demonstrated how compound matrices can be used to generalize contractive systems, diagonally stable systems, and positive/cooperative systems. 44