Compound interest MATHSWATCH CLIP 164 GRADE 5 L

Compound interest MATHSWATCH CLIP 164 GRADE 5 L. O. To be able to § Calculate compound interest and repeated percentage change Key Words interest, compound, repeated, increase, depreciate, annum, accrued

Compound interest MATHSWATCH CLIP 164 GRADE 5 COMPOUND INTEREST

Compound interest MATHSWATCH CLIP 164 GRADE 5 Interest § Interest is paid on amounts deposited in a bank account § An interest rate is given, as a percentage § Compound interest is the usual type of interest applied to bank accounts § Compound interest is when the interest each year is applied to the total amount in account at the end of that year (including previous interest paid)

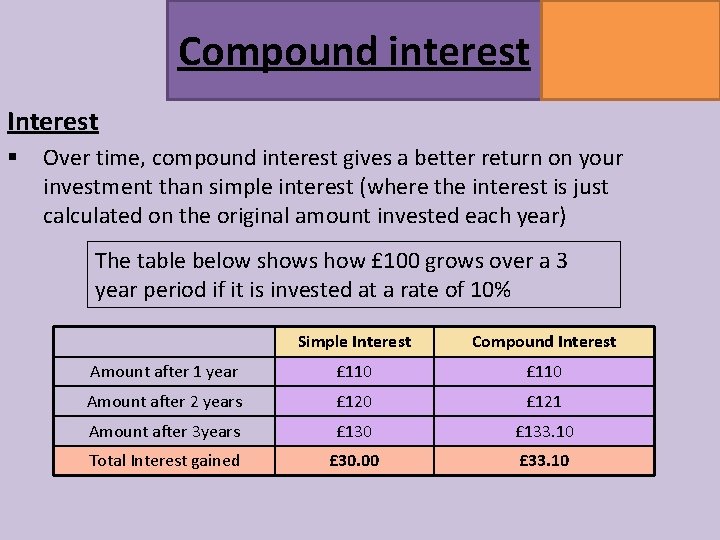
Compound interest MATHSWATCH CLIP 164 GRADE 5 Interest § Over time, compound interest gives a better return on your investment than simple interest (where the interest is just calculated on the original amount invested each year) The table below shows how £ 100 grows over a 3 year period if it is invested at a rate of 10% Simple Interest Compound Interest Amount after 1 year £ 110 Amount after 2 years £ 120 £ 121 Amount after 3 years £ 130 £ 133. 10 Total Interest gained £ 30. 00 £ 33. 10

Compound interest MATHSWATCH CLIP 164 GRADE 5 Example Jack puts £ 500 into a savings account with an annual compound interest rate of 5%. How much will he have in the account at the end of 4 years if he doesn’t add or withdraw any money? At the end of each year interest is added to the total amount in the account. This means that each year 5% of an ever larger amount is added to the account. To increase the amount in the account by 5% we need to multiply it by 105% or a percentage multiplier of 1. 05. We can do this for each year that the money is in the account.

Compound interest MATHSWATCH CLIP 164 GRADE 5 Example At the end of year 1 Jack has £ 500 × 1. 05 = £ 525 At the end of year 2 Jack has £ 525 × 1. 05 = £ 551. 25 At the end of year 3 Jack has £ 551. 25 × 1. 05 = £ 578. 81 At the end of year 4 Jack has £ 578. 81 × 1. 05 = £ 607. 75 (These amounts are written to the nearest penny. ) We can write this in a single calculation as £ 500 × 1. 05 = £ 607. 75 Or using index notation as £ 500 × 1. 054 = £ 607. 75

Difficulty * Compound interest MATHSWATCH CLIP 164 GRADE 5 Example How much would Jack have after 10 years? How long would it take for the money to double?

Difficulty * Compound interest MATHSWATCH CLIP 164 GRADE 5 Example How much would Jack have after 10 years? After 10 years the investment would be worth £ 500 × 1. 0510 = £ 814. 45 (to the nearest 1 p) How long would it take for the money to double? Using trial and improvement, £ 500 × 1. 0514 = £ 989. 97 (to the nearest 1 p) £ 500 × 1. 0515 = £ 1039. 46 (to the nearest 1 p) It would take 15 years for the money to double.

Compound interest MATHSWATCH CLIP 164 GRADE 5 Compound interest To work out the value of an investment, at a given compound interest rate, for a given number of years… § First take your percentage interest rate and write as a multiplier for an increase by that percentage (x 1. _ _ ) § Use this formula:

Compound interest Example £ 500 is put into a bank account paying 5% interest per annum. How much will there be after 2 years ? Total amount after 2 years = 500 x 1. 052 = £ 551. 25 MATHSWATCH CLIP 164 GRADE 5

Difficulty * Compound interest Example £ 2000 is put into a bank account paying 12% interest per annum. How much will there be after 3 years ? MATHSWATCH CLIP 164 GRADE 5

Difficulty * Compound interest Example £ 2000 is put into a bank account paying 12% interest per annum. How much will there be after 3 years ? Total amount after 3 years = 2508. 80 x 1. 123 = £ 2809. 86 MATHSWATCH CLIP 164 GRADE 5

Difficulty ** Compound interest Task 1) £ 240 at 10 % p. a. for 2 years. 2) £ 800 at 4 % p. a. for 2 years. 3) £ 15000 at 8 ½ % p. a. for 2 years. 4) £ 7000 at 15 % p. a. for 3 years. 5) £ 50000 at 12 ¼ % p. a. for 3 years. MATHSWATCH CLIP 164 GRADE 5

Difficulty ** Compound interest MATHSWATCH CLIP 164 GRADE 5 Task 1) £ 240 at 10 % p. a. for 2 years. £ 290. 40 2) £ 800 at 4 % p. a. for 2 years. £ 865. 28 3) £ 15000 at 8 ½ % p. a. for 2 years. £ 17658. 38 4) £ 7000 at 15 % p. a. for 3 years. £ 10646. 13 5) £ 50000 at 12 ¼ % p. a. for 3 years. £ 70717. 85

Difficulty *** Compound interest MATHSWATCH CLIP 164 GRADE 5 Task Q 1. £ 8000 is invested at 7% compound interest for 6 years. Find: (a) the amount in the account at the end of the period (nearest £) and (b) the interest accrued (nearest £) Q 2. £ 1250 is invested at 9% compound interest for 10 years. Find: (a) the amount in the account at the end of the period (nearest £) and (b) the interest accrued (nearest £) Q 3. £ 3750 is invested at 4. 5% compound interest for 8 years. Find the amount in the account at the end of the period (nearest £ 100) Q 4. £ 7500 is invested at 8. 5% compound interest for 15 years. Find the amount in the account at the end of the period (nearest £ 100)

Difficulty *** Compound interest MATHSWATCH CLIP 164 GRADE 5 Solutions Question 1 £ 8000 is invested at 7% compound interest for 6 years. Find: (a) the amount in the account at the end of the period (nearest £) and (b) the interest accrued (nearest £) (a) 8000 x 1. 076 = £ 12, 006 (b) 12, 006 – 8000 = £ 4, 006 Question 2 £ 1250 is invested at 9% compound interest for 10 years. Find: (a) the amount in the account at the end of the period (nearest £) and (b) the interest accrued (nearest £) (a) 1250 x 1. 0910 = £ 2959 (b) 2959 – 1250 = £ 1709

Difficulty *** Compound interest MATHSWATCH CLIP 164 GRADE 5 Solutions Question 5 £ 3750 is invested at 4. 5% compound interest for 8 years. Find the amount in the account at the end of the period (nearest £ 100) Answer: 3750 x 1. 0458 = £ 5300 Question 6 £ 7500 is invested at 8. 5% compound interest for 15 years. Find the amount in the account at the end of the period (nearest £ 100) Answer: 7500 x 1. 08515 = £ 25 500

Compound interest MATHSWATCH CLIP 164 GRADE 5 REPEATED PERCENTAGE CHANGE

Compound interest MATHSWATCH CLIP 164 GRADE 5 We can use the “compound interest” formula to help solve many problems involving repeated percentage increase and decrease. The population of a village increases by 2% each year. If the current population is 2345, what will it be in 5 years? To increase the population by 2% we multiply it by 1. 02. After 5 years the population will be 2345 × 1. 025 = 2589 (to the nearest whole) What will the population be after 10 years? After 5 years the population will be 2345 × 1. 0210 = 2859 (to the nearest whole)

Compound interest MATHSWATCH CLIP 164 GRADE 5 The value of a new car depreciates at a rate of 15% a year. The car costs £ 24 000 in 2005. How much will it be worth in 2013? To decrease the value by 15% we multiply it by 0. 85. There are 8 years between 2005 and 2013. After 8 years the value of the car will be £ 24 000 × 0. 858 = £ 6540 (to the nearest pound)

Compound interest MATHSWATCH CLIP 164 GRADE 5 § Sometimes repeated percentage change involves the percentage itself differing over time, or an increase being followed by a decrease § The next examples involve these types of problems

Compound interest MATHSWATCH CLIP 164 GRADE 5 A jacket is reduced by 20% in a sale. Two weeks later the shop reduces the price by a further 10%. What is the total percentage discount? It is not 30%! When a percentage change is followed by another percentage change do not add the percentages together to find the total percentage change. The second percentage change is found on a new amount and not on the original amount.

Compound interest MATHSWATCH CLIP 164 GRADE 5 A jacket is reduced by 20% in a sale. Two weeks later the shop reduces the price by a further 10%. What is the total percentage discount? To find a 20% decrease we multiply by 80% or 0. 8. To find a 10% decrease we multiply by 90% or 0. 9. A 20% discount followed by a 10% discount is equivalent to multiplying the original price by 0. 8 and then by 0. 9. original price × 0. 8 × 0. 9 = original price × 0. 72

Compound interest MATHSWATCH CLIP 164 GRADE 5 A jacket is reduced by 20% in a sale. Two weeks later the shop reduces the price by a further 10%. What is the total percentage discount? The sale price is 72% of the original price. This is equivalent to a 28% discount. A 20% discount followed by a 10% discount A 28% discount

Difficulty ** Compound interest MATHSWATCH CLIP 164 GRADE 5 Problem solving! Jenna invests in some shares. After one week the value goes up by 10%. The following week they go down by 10%. Has Jenna made a loss, a gain or is she back to her original investment?

Difficulty ** Compound interest MATHSWATCH CLIP 164 GRADE 5 Solution To find a 10% increase we multiply by 110% or 1. 1. To find a 10% decrease we multiply by 90% or 0. 9. original amount × 1. 1 × 0. 9 = original amount × 0. 99 Fiona has 99% of her original investment and has therefore made a 1% loss.

Compound interest MATHSWATCH CLIP 164 GRADE 5 Repeated percentage change § Work out the percentage multipliers for each change which is to be applied § Multiply these decimals together to find the overall percentage multiplier § This can be used to: § calculate the final value, or § decide what the overall percentage change would be