COMPOUND ANGLE FORMULAE sinA B Draw a horizontal
COMPOUND ANGLE FORMULAE: sin(A + B) Draw a horizontal base line.
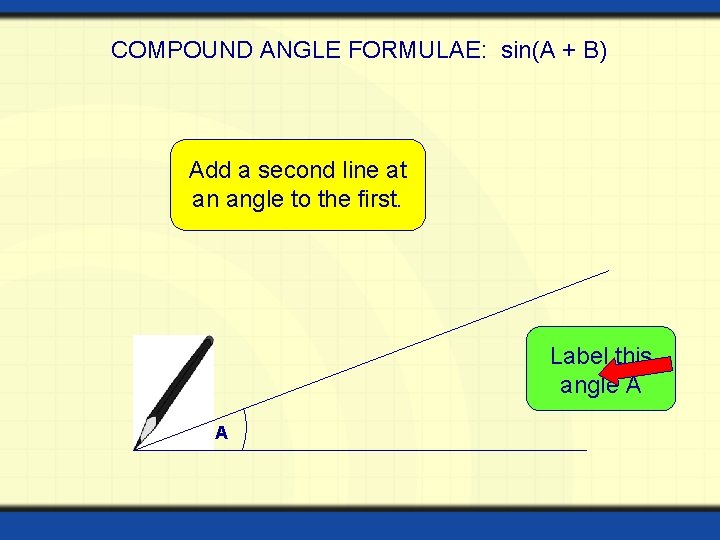
COMPOUND ANGLE FORMULAE: sin(A + B) Add a second line at an angle to the first. Label this angle A A
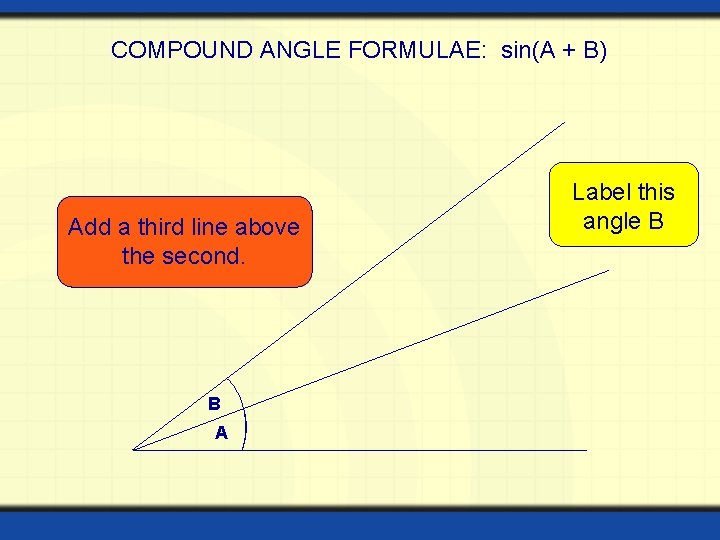
COMPOUND ANGLE FORMULAE: sin(A + B) Add a third line above the second. B A Label this angle B
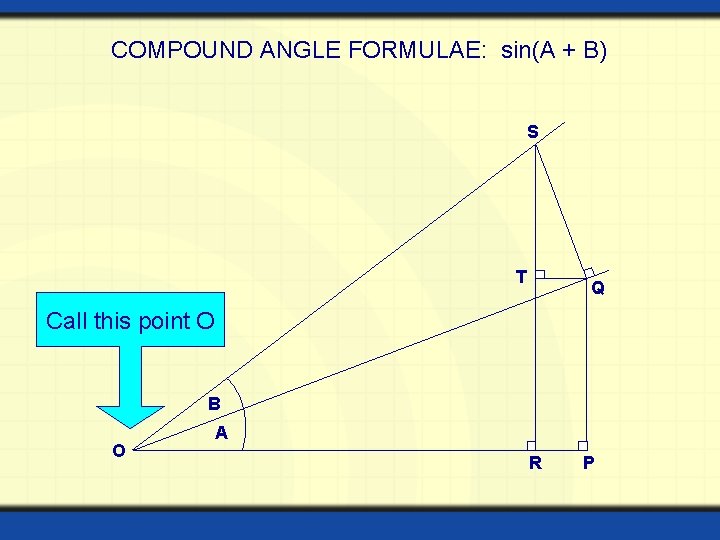
COMPOUND ANGLE FORMULAE: sin(A + B) S T Q Call this point O B O A R P
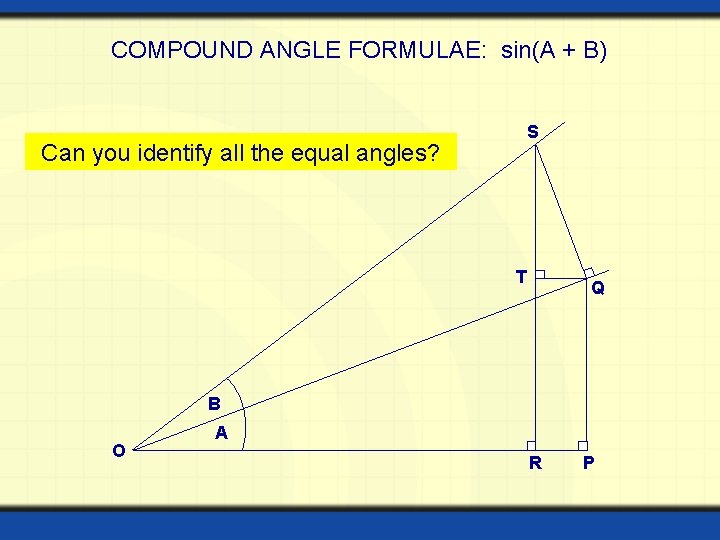
COMPOUND ANGLE FORMULAE: sin(A + B) Can you identify all the equal angles? S T Q B O A R P
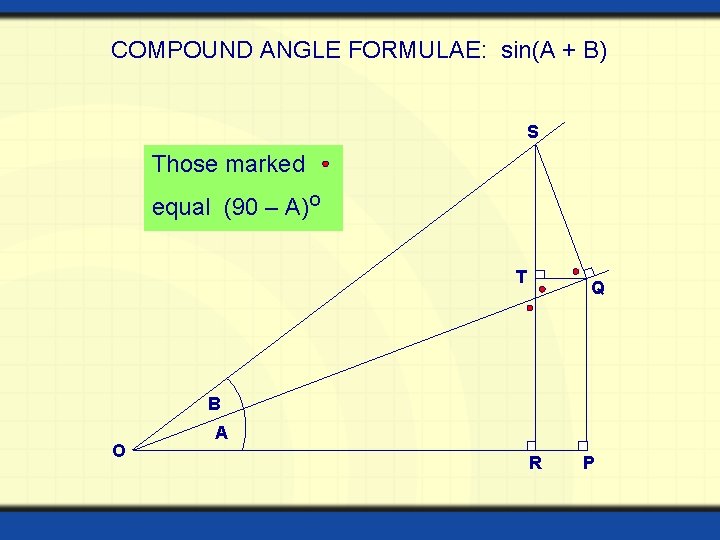
COMPOUND ANGLE FORMULAE: sin(A + B) S Those marked equal (90 – A)o T Q B O A R P
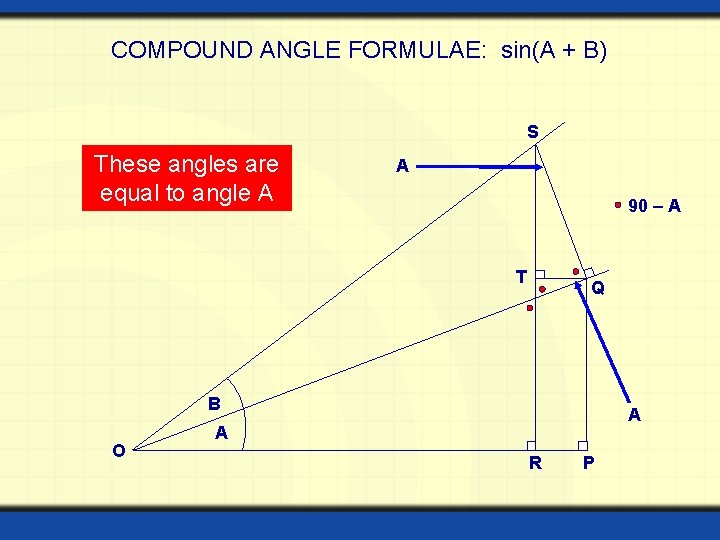
COMPOUND ANGLE FORMULAE: sin(A + B) S These angles are equal to angle A A 90 – A T Q B O A A R P
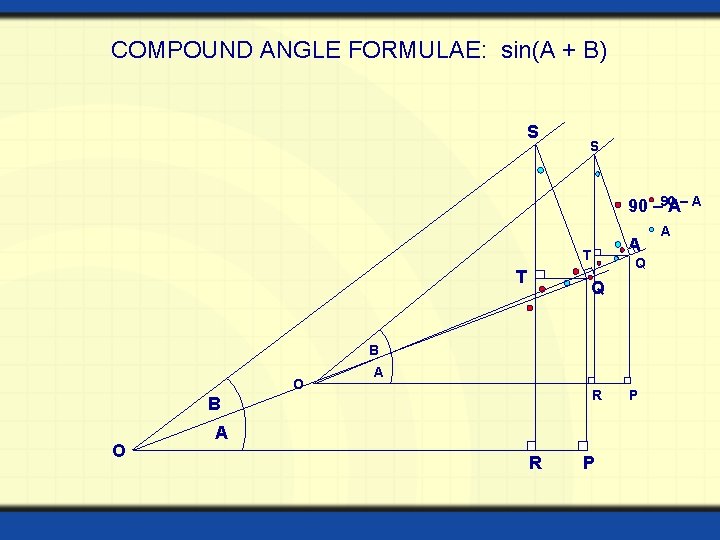
COMPOUND ANGLE FORMULAE: sin(A + B) S S 90 – 90 A– A A T T Q Q B O A R P P A
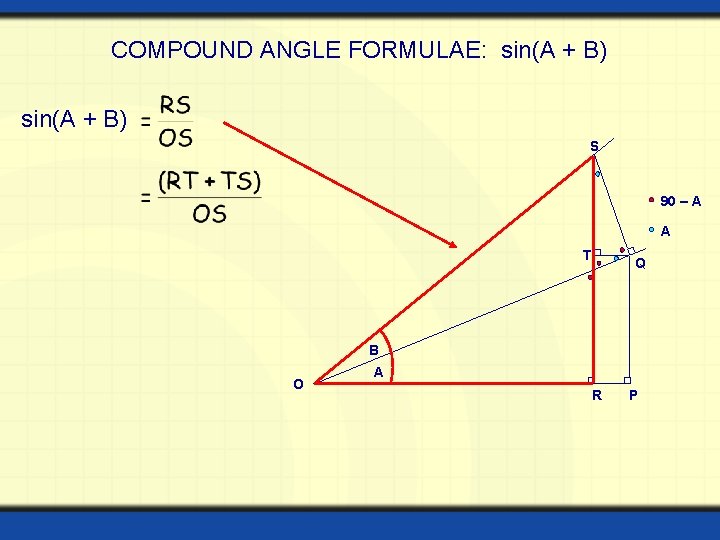
COMPOUND ANGLE FORMULAE: sin(A + B) S 90 – A A T Q B O A R P
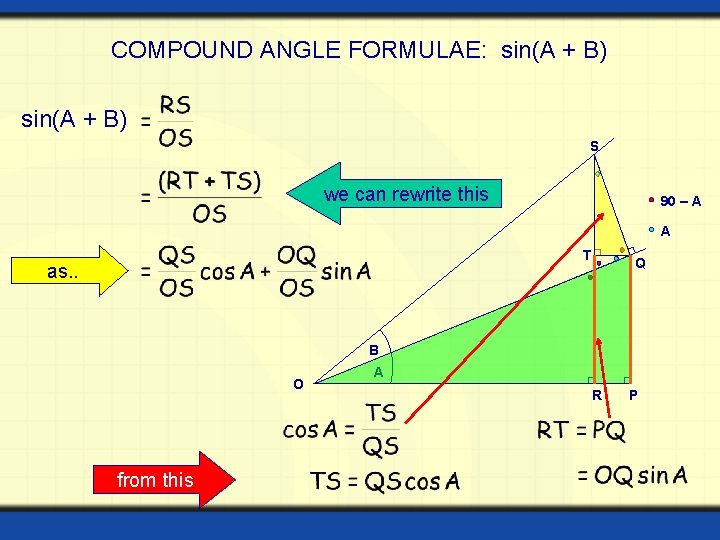
COMPOUND ANGLE FORMULAE: sin(A + B) S we can rewrite this 90 – A A T as. . Q B O from this A R P
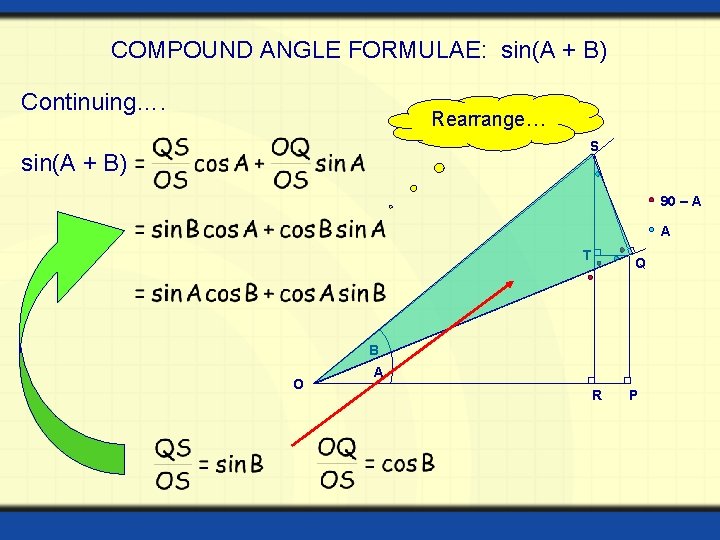
COMPOUND ANGLE FORMULAE: sin(A + B) Continuing…. Rearrange… S sin(A + B) 90 – A A T Q B O A R P
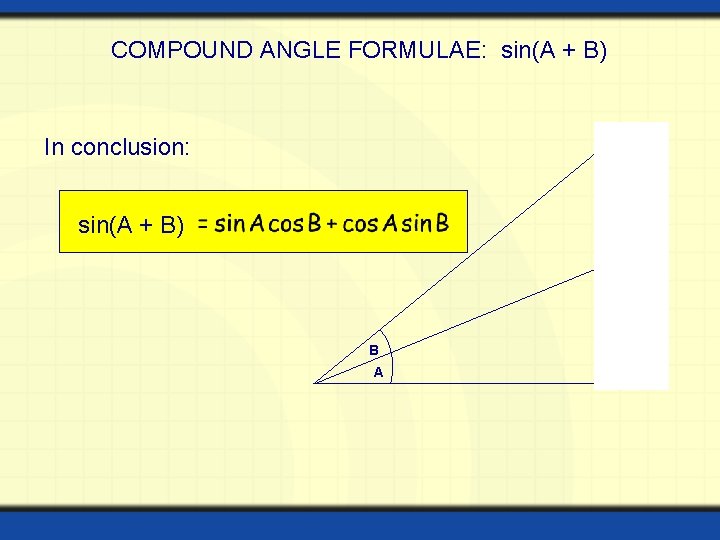
COMPOUND ANGLE FORMULAE: sin(A + B) In conclusion: sin(A + B) B A

If we replace B by (-B) in formula of sin(A – B), we have

If we replace A by ( /2 - A) in the formula of sin(A - B), we have

By substituting (- B) in the formula of cos(A + B), we have

From the quotient relation and the above formulae,

By substituting (-B) for B in the formula tan(A + B)


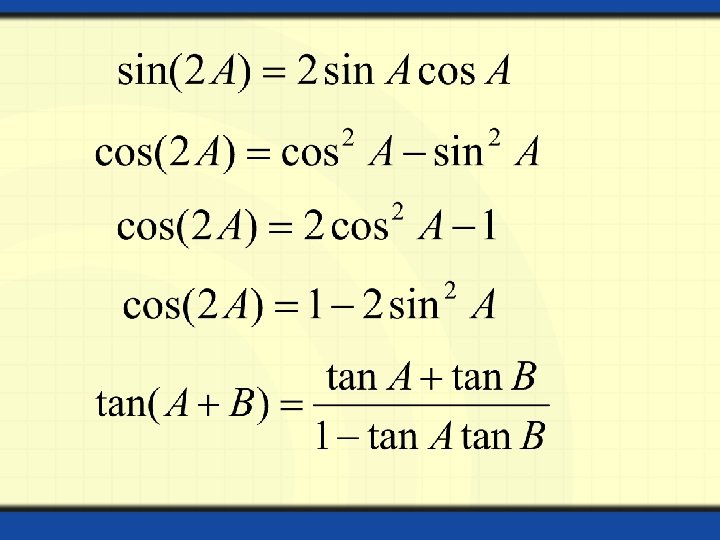
- Slides: 20