Compose de deux translations Relation de Chasles Somme

Composée de deux translations Relation de Chasles Somme de deux vecteurs "l'un à la suite de l'autre" a) b) c) Somme de deux vecteurs de même origine d) e) f) Somme de deux vecteurs d'origine quelconque g) h) i) Vecteurs opposés Composée de deux symétries centrales j)

Composée de deux translations

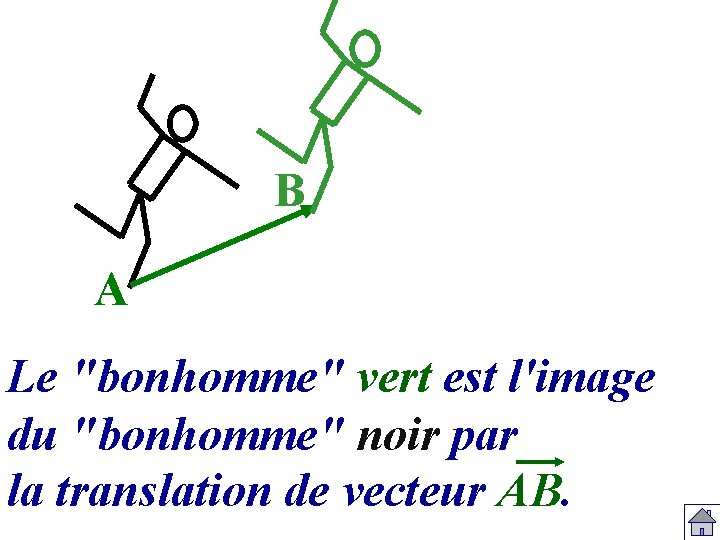
B A Le "bonhomme" vert est l'image du "bonhomme" noir par la translation de vecteur AB.

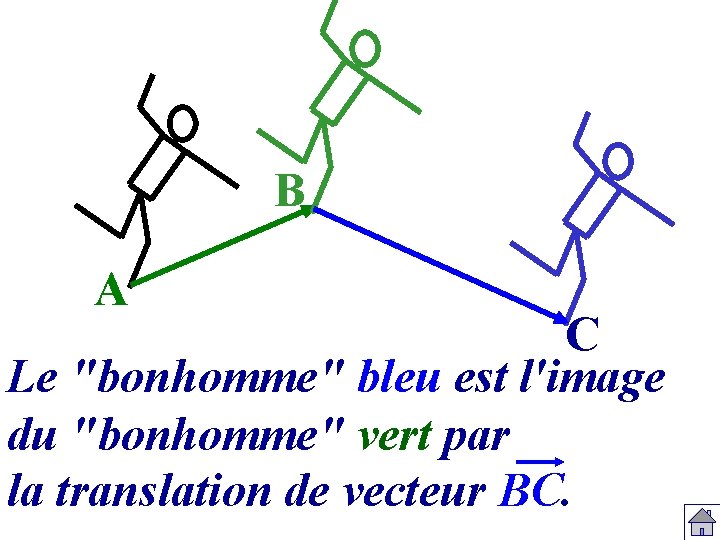
B A C Le "bonhomme" bleu est l'image du "bonhomme" vert par la translation de vecteur BC.

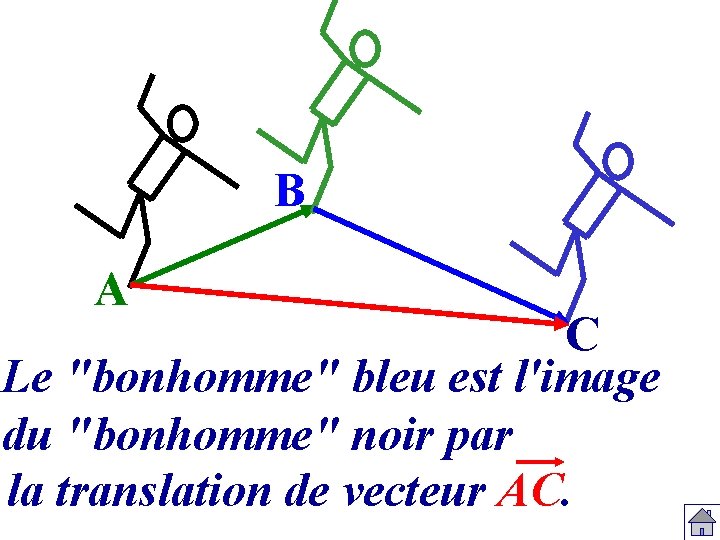
B A C Le "bonhomme" bleu est l'image du "bonhomme" noir par la translation de vecteur AC.

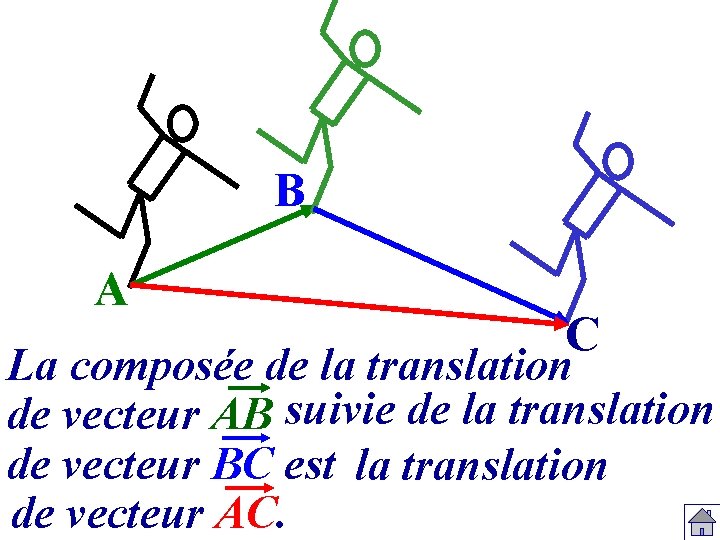
B A C La composée de la translation de vecteur AB suivie de la translation de vecteur BC est la translation de vecteur AC.

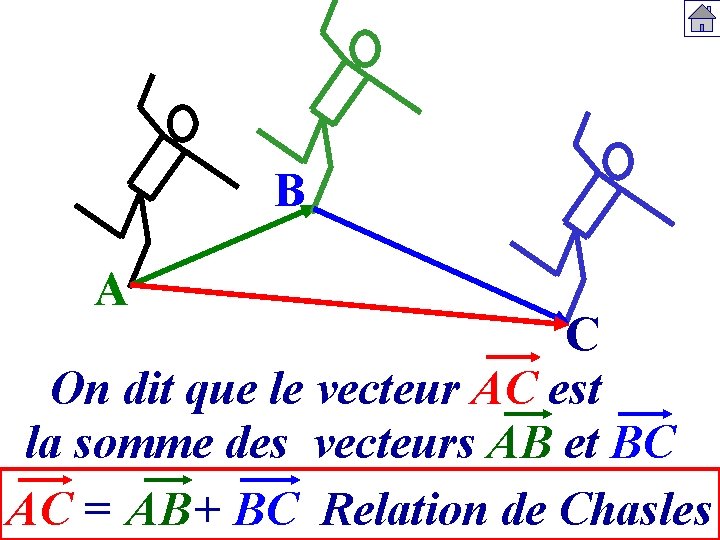
B A C On dit que le vecteur AC est la somme des vecteurs AB et BC AC = AB+ BC Relation de Chasles

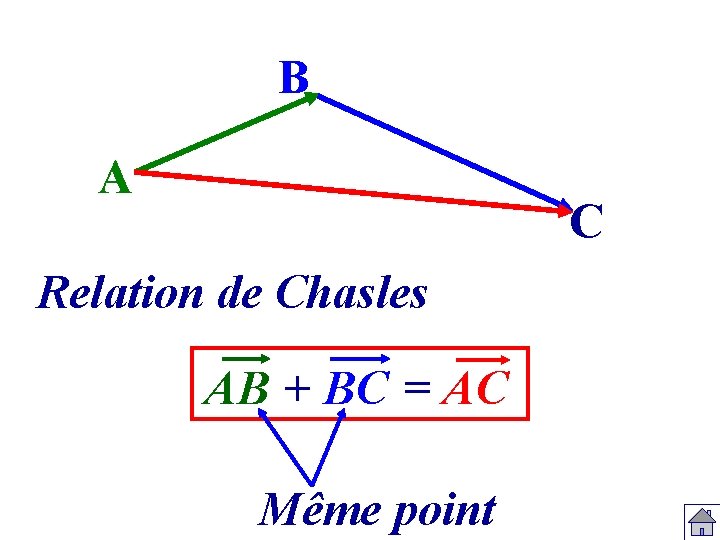
B A C Relation de Chasles AB + BC = AC Même point

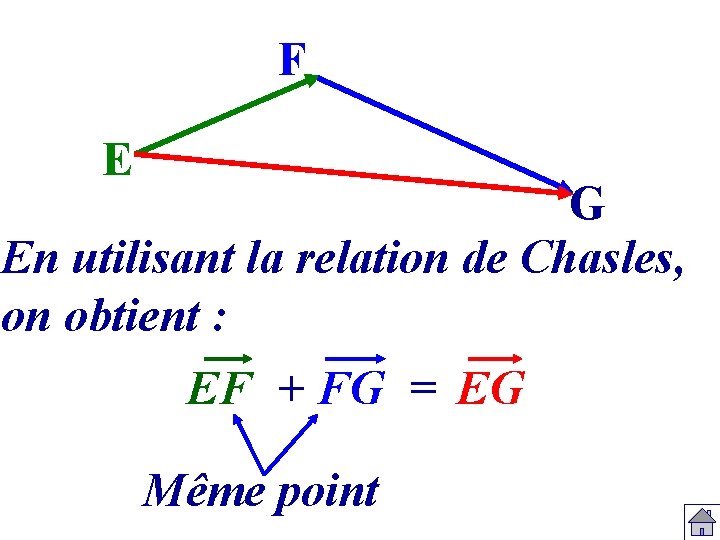
F E G En utilisant la relation de Chasles, on obtient : EF + FG = EG Même point

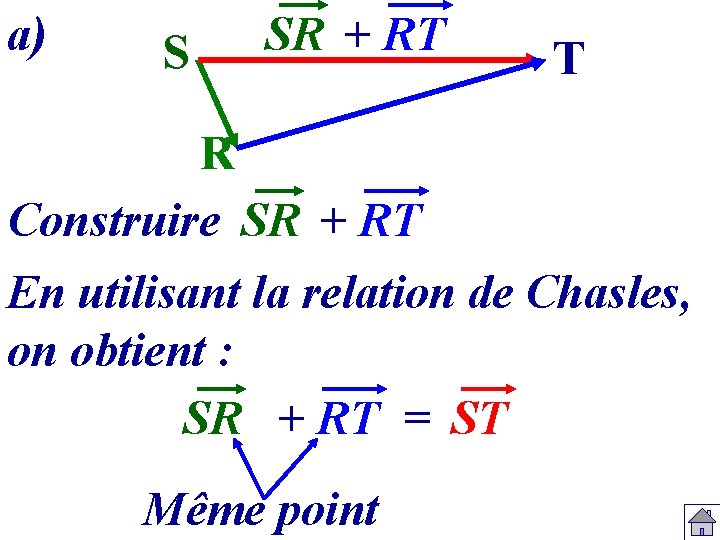
a) S SR + RT T R Construire SR + RT En utilisant la relation de Chasles, on obtient : SR + RT = ST Même point

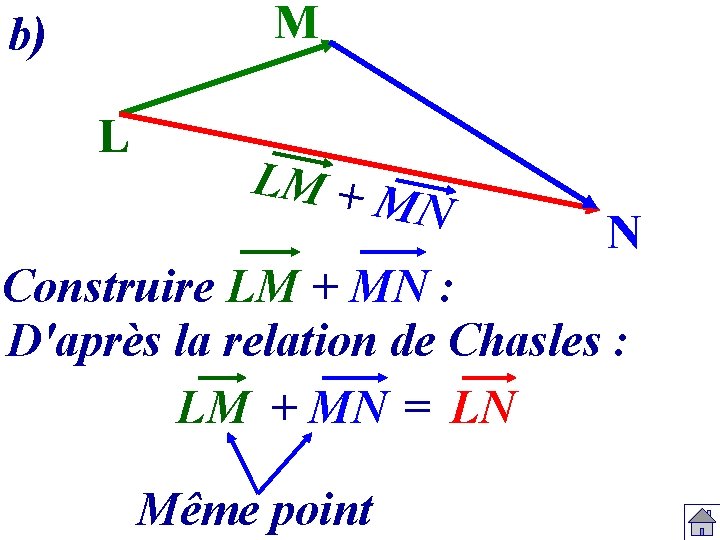
M b) L LM + M N N Construire LM + MN : D'après la relation de Chasles : LM + MN = LN Même point

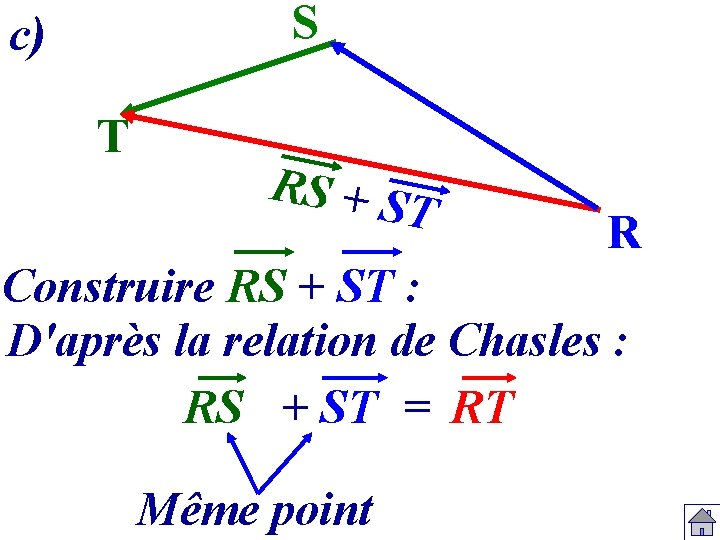
S c) T RS + S T R Construire RS + ST : D'après la relation de Chasles : RS + ST = RT Même point

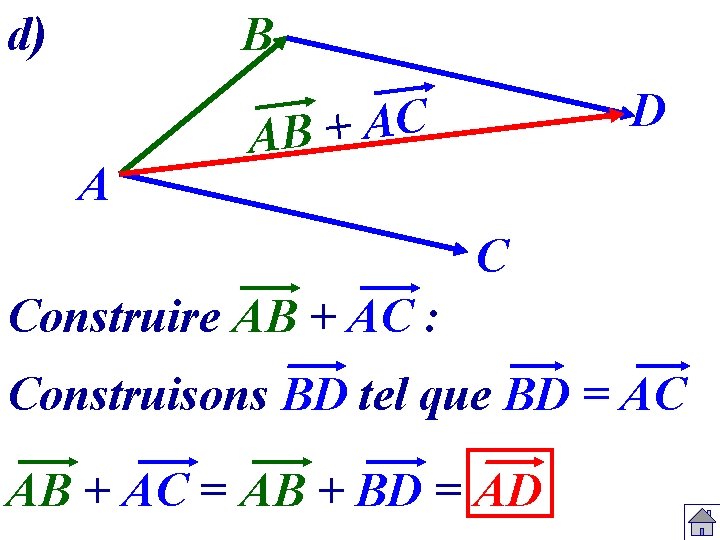
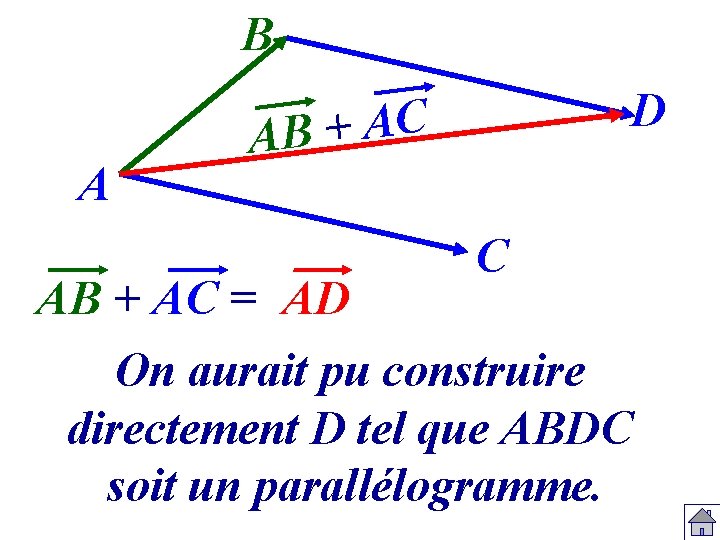
d) B A D C A + AB C Construire AB + AC : Construisons BD tel que BD = AC AB + AC = AB + BD = AD

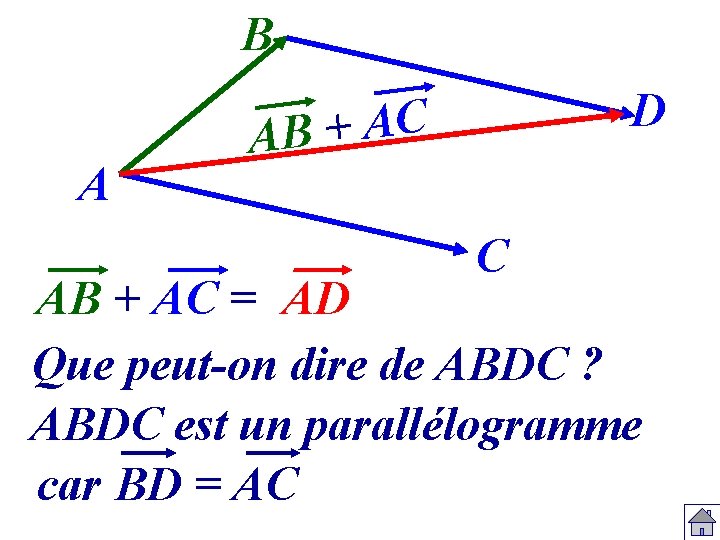
B A D C A + AB C AB + AC = AD Que peut-on dire de ABDC ? ABDC est un parallélogramme car BD = AC

B A D C A + AB AB + AC = AD C On aurait pu construire directement D tel que ABDC soit un parallélogramme.

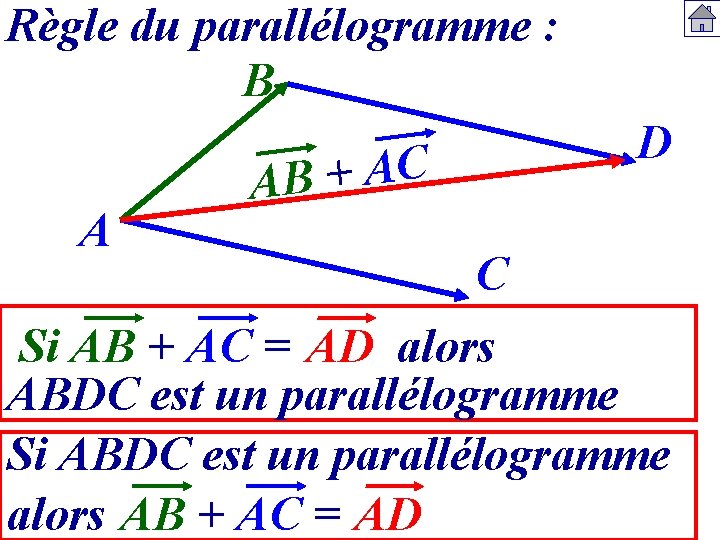
Règle du parallélogramme : B A D C A + B A C Si AB + AC = AD alors ABDC est un parallélogramme Si ABDC est un parallélogramme alors AB + AC = AD

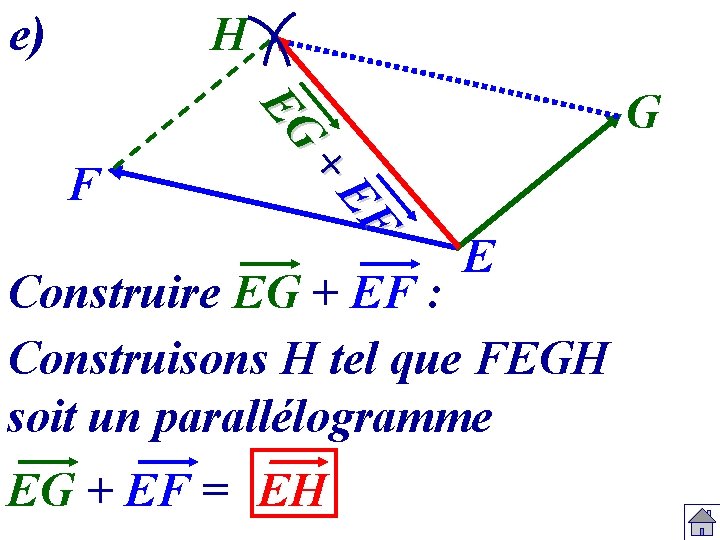
e) H EG G EF + F E Construire EG + EF : Construisons H tel que FEGH soit un parallélogramme EG + EF = EH

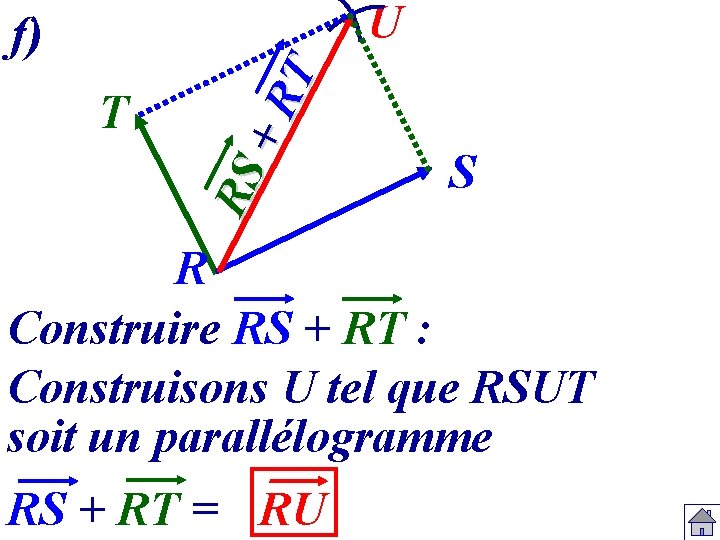
U RS + T RT f) S R Construire RS + RT : Construisons U tel que RSUT soit un parallélogramme RS + RT = RU

Somme de deux vecteurs d'origine quelconque

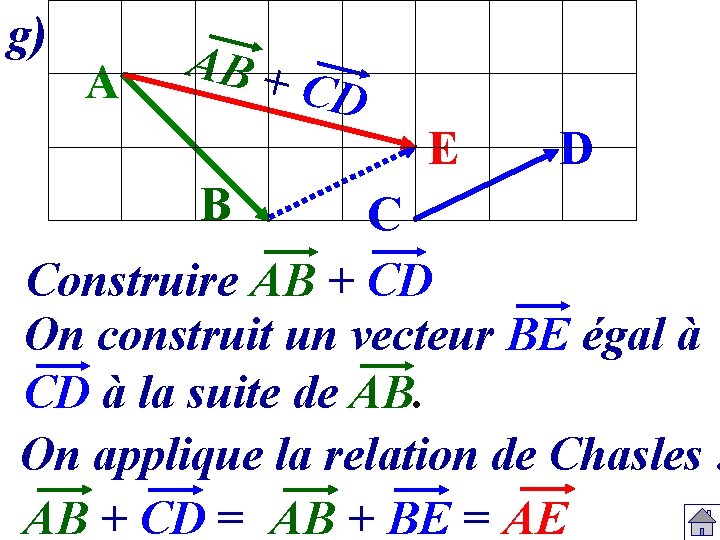
g) A AB + B CD E D C Construire AB + CD On construit un vecteur BE égal à CD à la suite de AB. On applique la relation de Chasles : AB + CD = AB + BE = AE

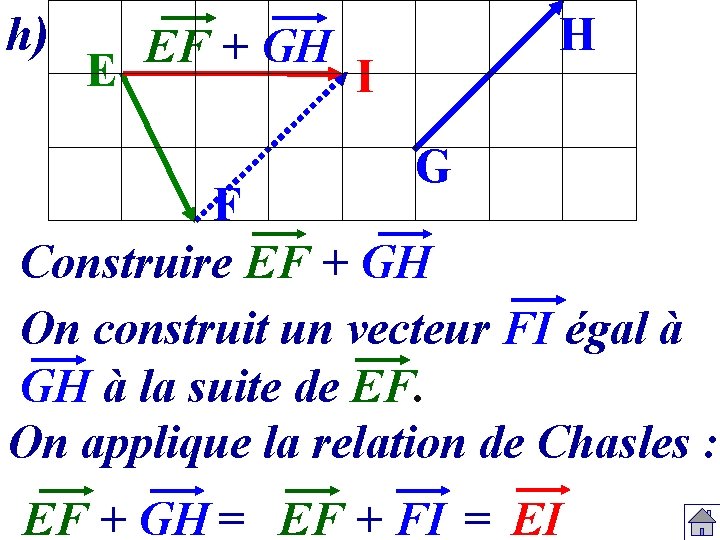
h) H EF + GH E I G F Construire EF + GH On construit un vecteur FI égal à GH à la suite de EF. On applique la relation de Chasles : EF + GH = EF + FI = EI

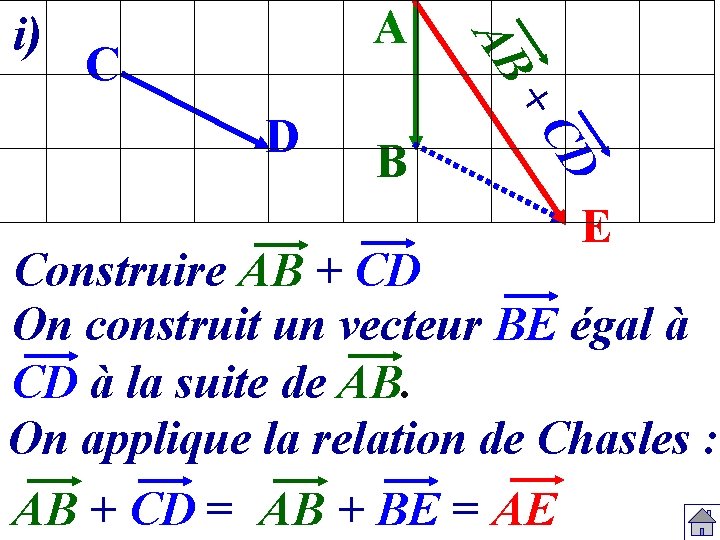
A C D B +C D AB i) E Construire AB + CD On construit un vecteur BE égal à CD à la suite de AB. On applique la relation de Chasles : AB + CD = AB + BE = AE

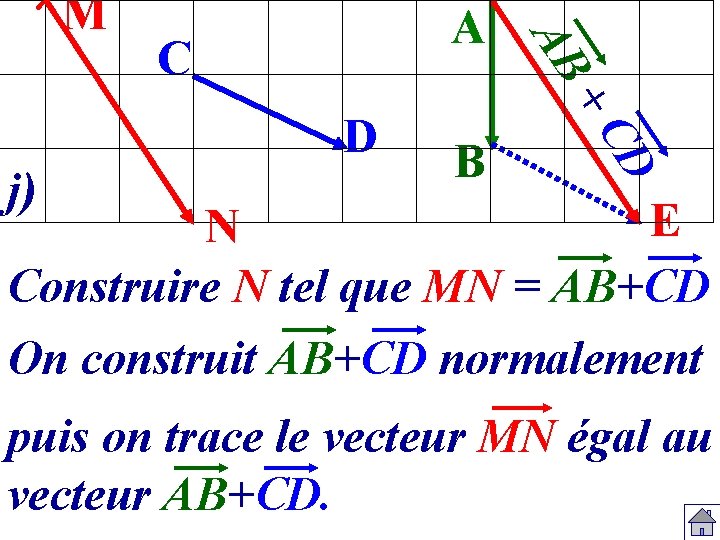
A C D j) B +C D AB M E N Construire N tel que MN = AB+CD On construit AB+CD normalement puis on trace le vecteur MN égal au vecteur AB+CD.

Vecteurs opposés

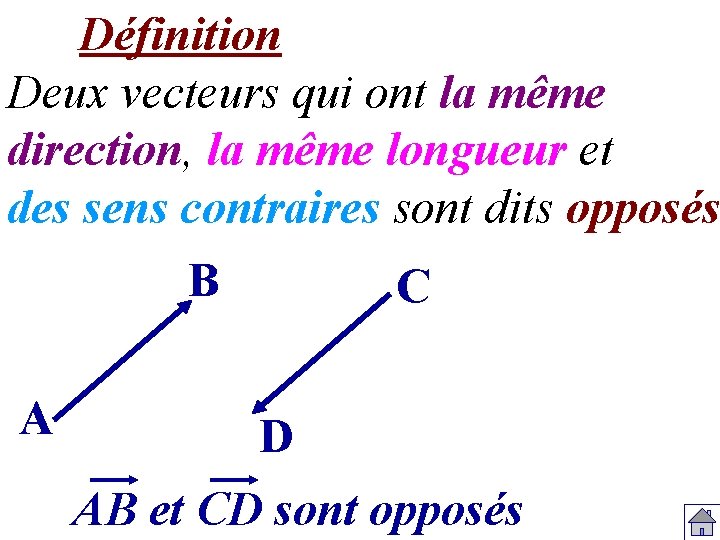
Définition Deux vecteurs qui ont la même direction, la même longueur et des sens contraires sont dits opposés B A C D AB et CD sont opposés

Définition Deux vecteurs qui ont la même direction, la même longueur et des sens contraires sont dits opposés Cas particulier : B AB et BA sont opposés AB + BA = AA = 0 A Vecteur nul On écrit BA = -AB

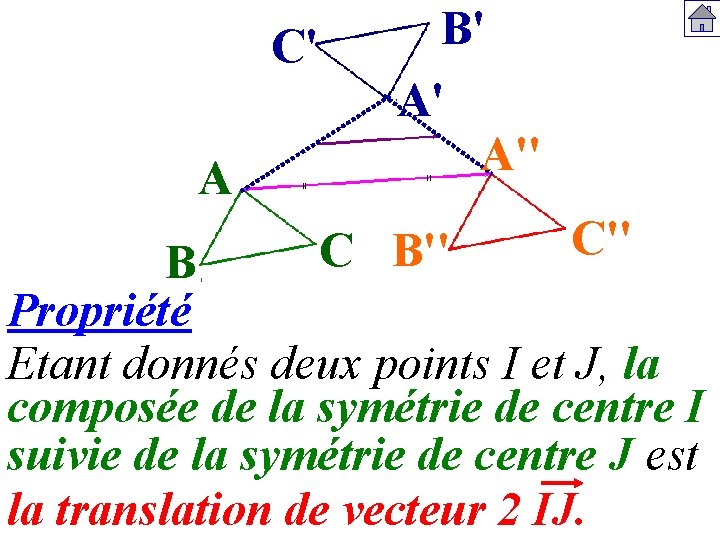
C' A B' A' A'' C B'' C'' B Propriété Etant donnés deux points I et J, la composée de la symétrie de centre I suivie de la symétrie de centre J est la translation de vecteur 2 IJ.

Fin