Components of Vectors This vector represents a path

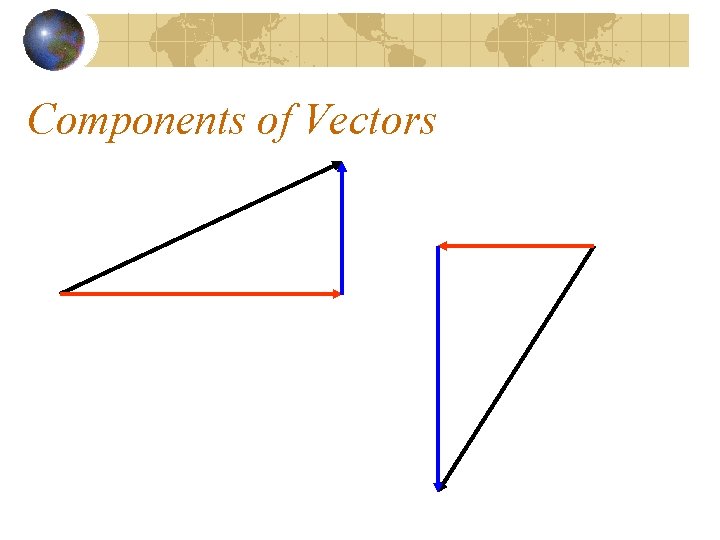
Components of Vectors

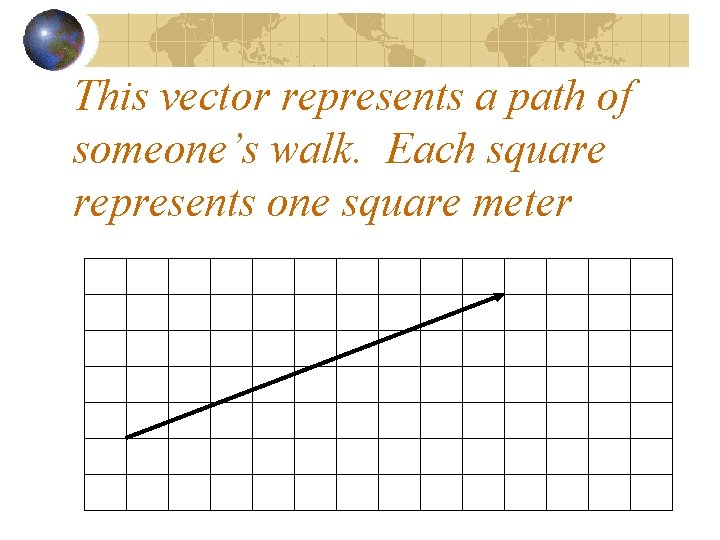
This vector represents a path of someone’s walk. Each square represents one square meter

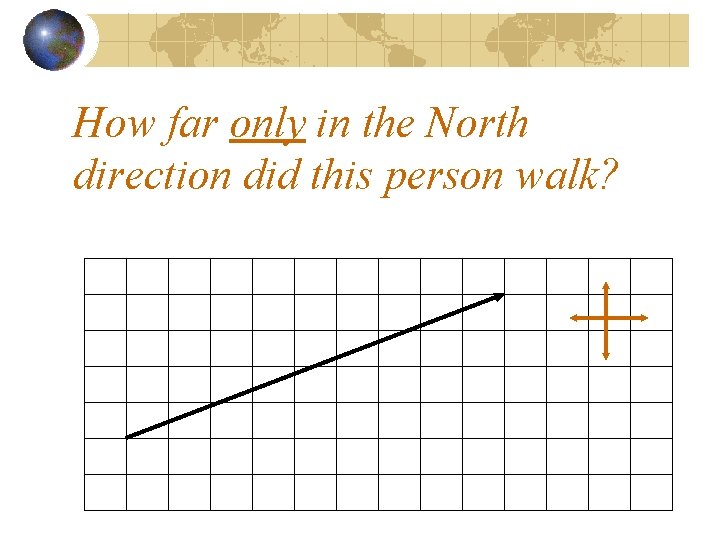
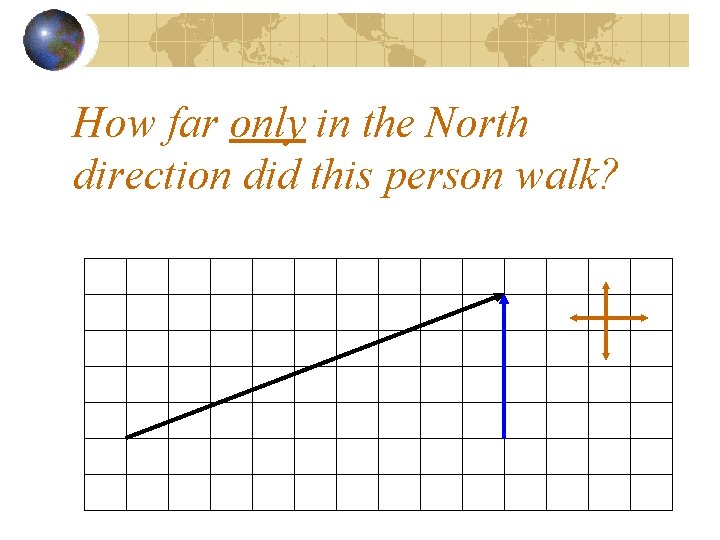
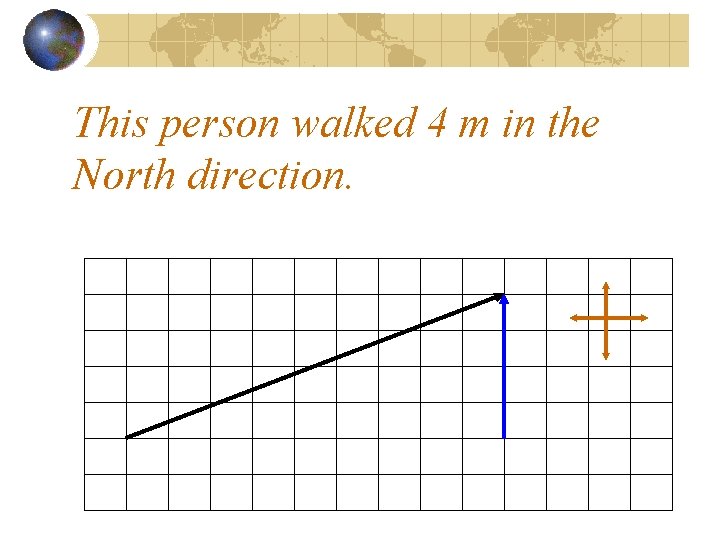
How far only in the North direction did this person walk?

How far only in the North direction did this person walk?

This person walked 4 m in the North direction.

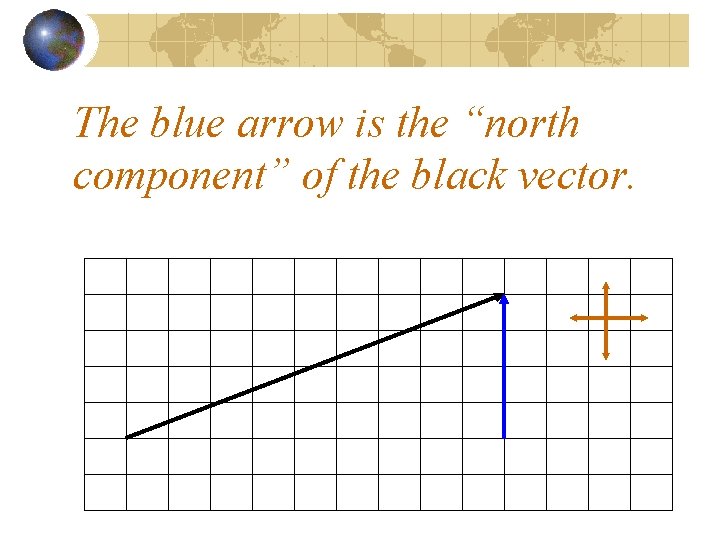
The blue arrow is the “north component” of the black vector.

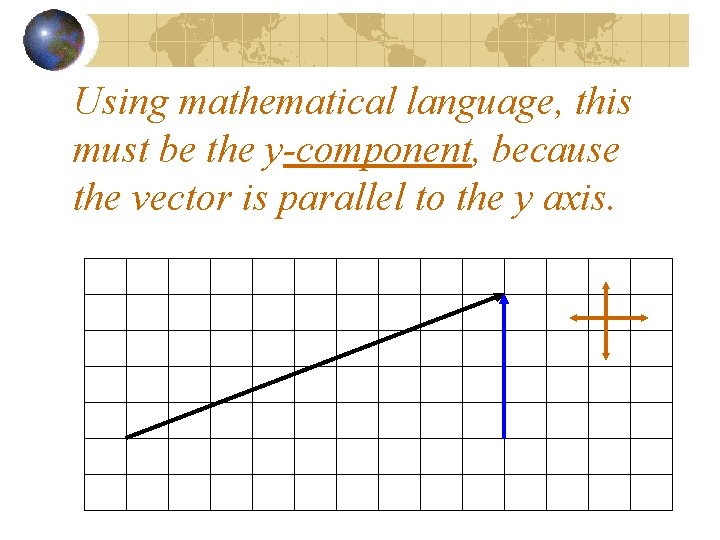
Using mathematical language, this must be the component

Using mathematical language, this must be the y-component, because the vector is parallel to the y axis.

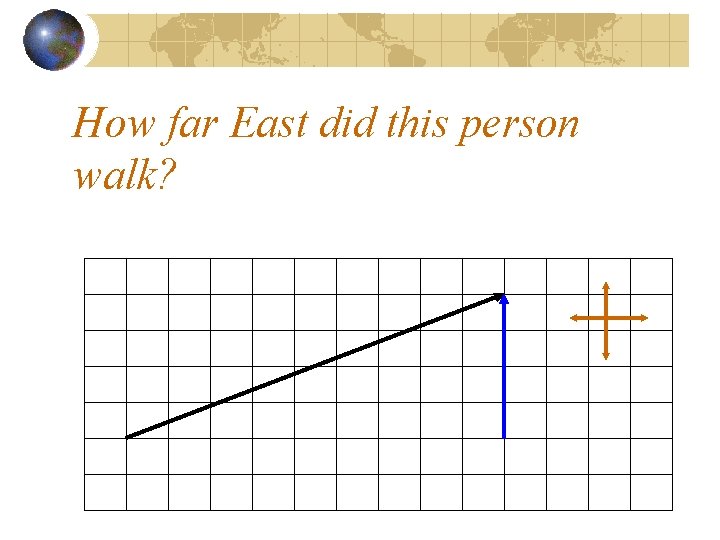
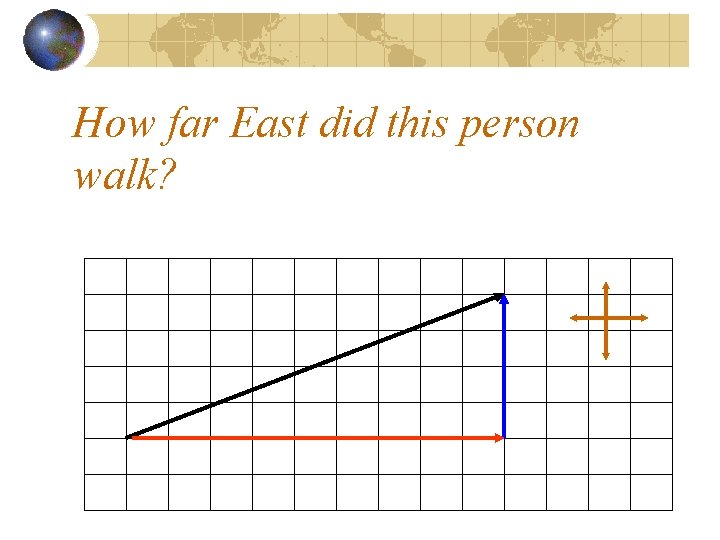
How far East did this person walk?

How far East did this person walk?

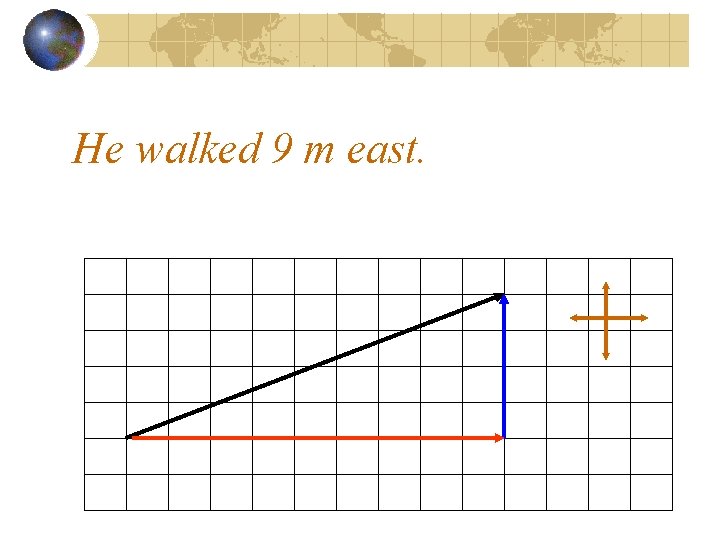
He walked 9 m east.

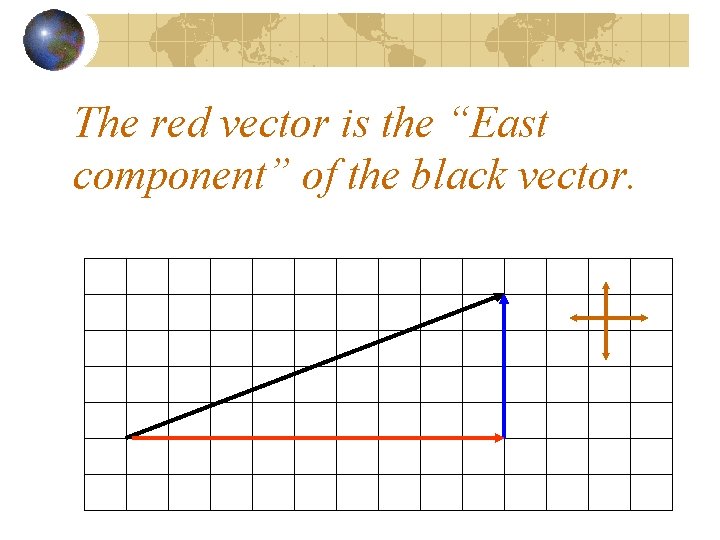
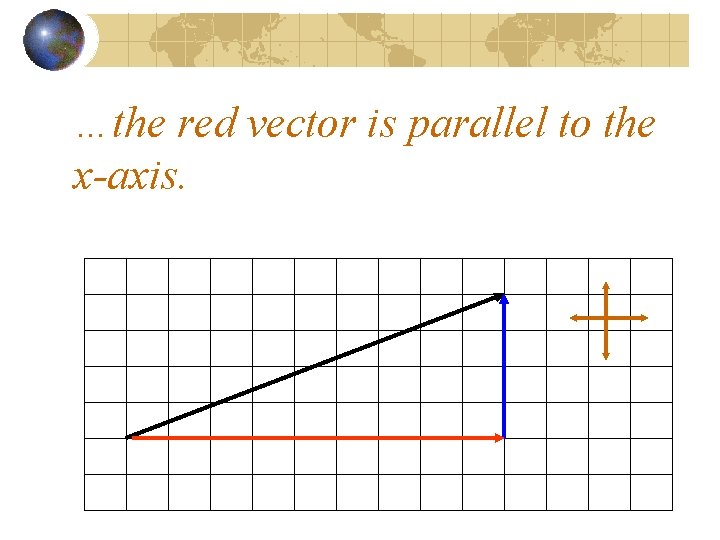
The red vector is the “East component” of the black vector.

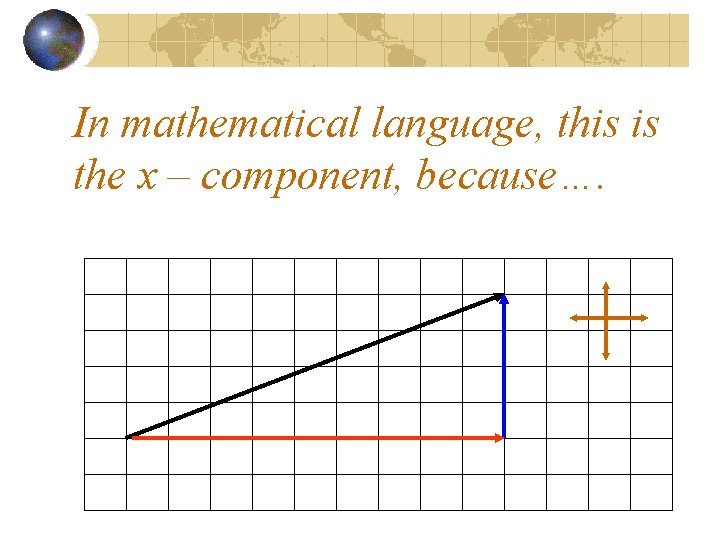
In mathematical language, this is the __ component

In mathematical language, this is the x – component, because….

…the red vector is parallel to the x-axis.

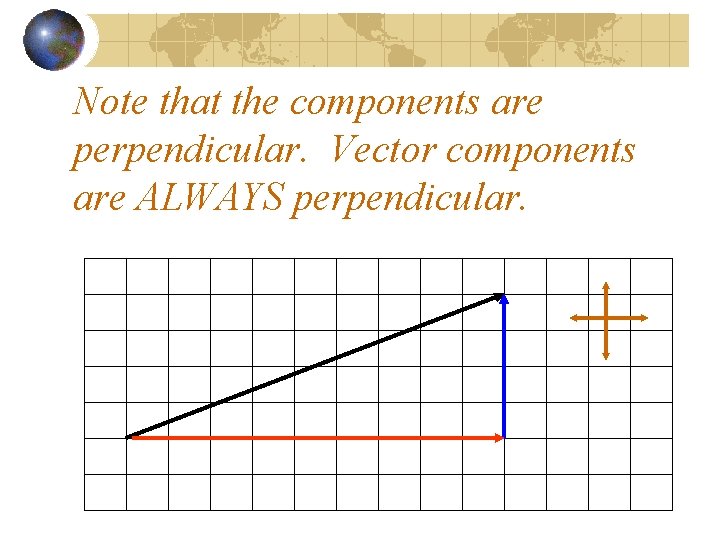
Note that the components are perpendicular. Vector components are ALWAYS perpendicular.

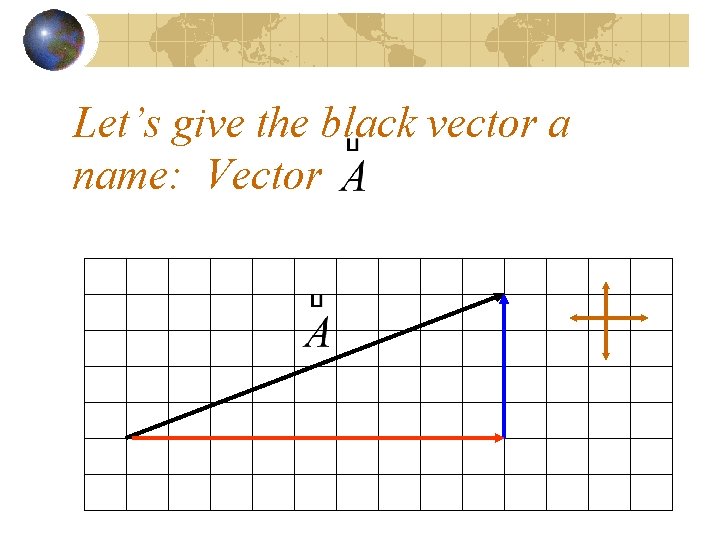
Let’s give the black vector a name: Vector

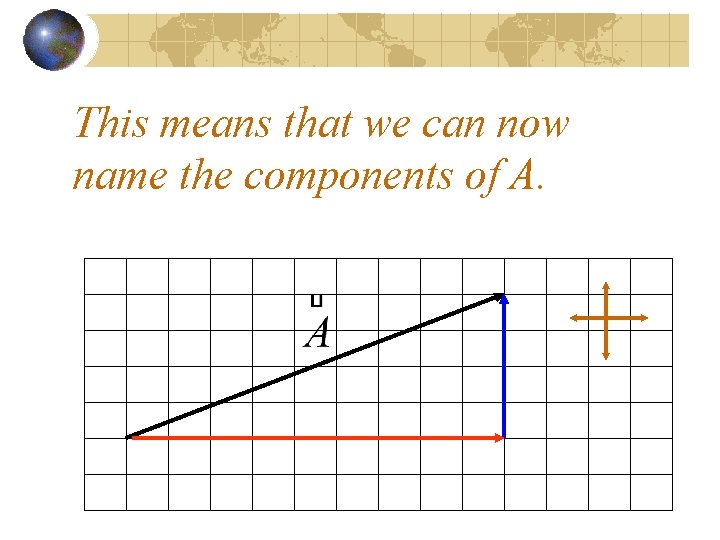
This means that we can now name the components of A.

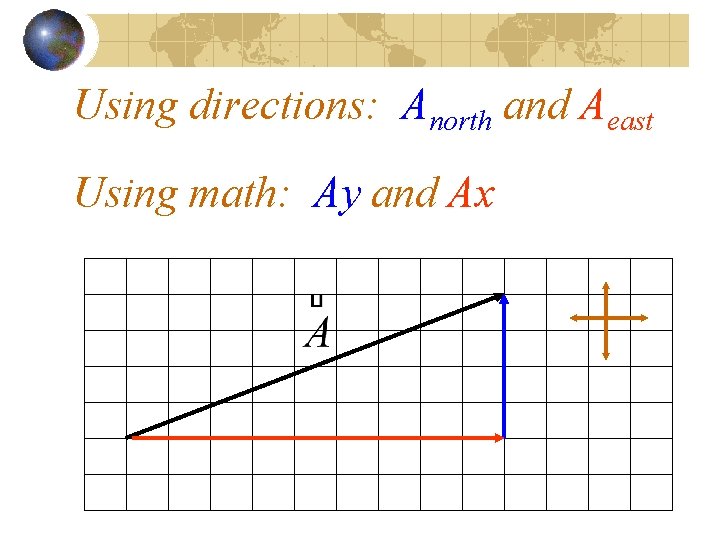
Using directions: Anorth and Aeast Using math: Ay and Ax

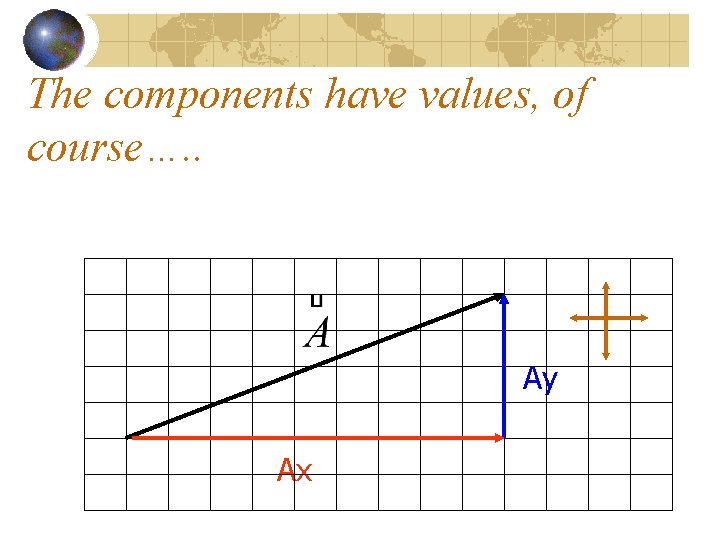
The components have values, of course…. . Ay Ax

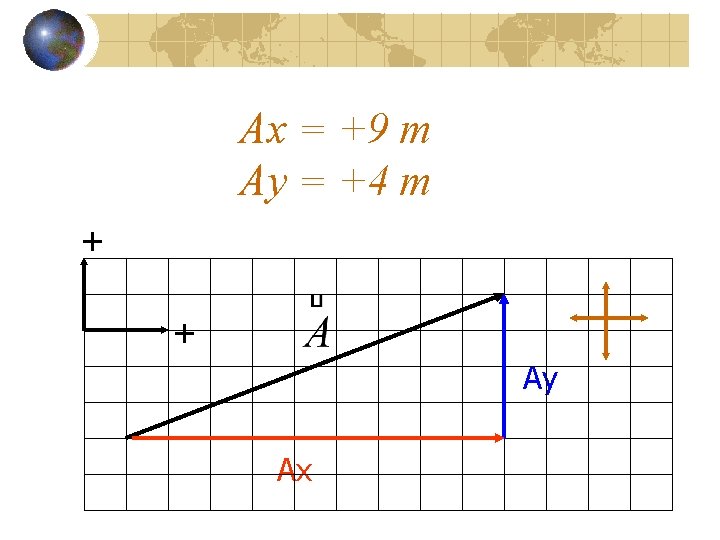
Ax = +9 m Ay = +4 m + + Ay Ax

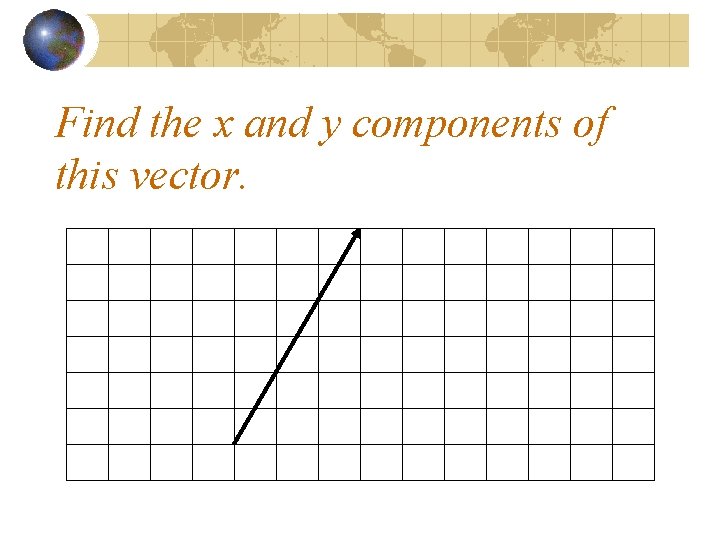
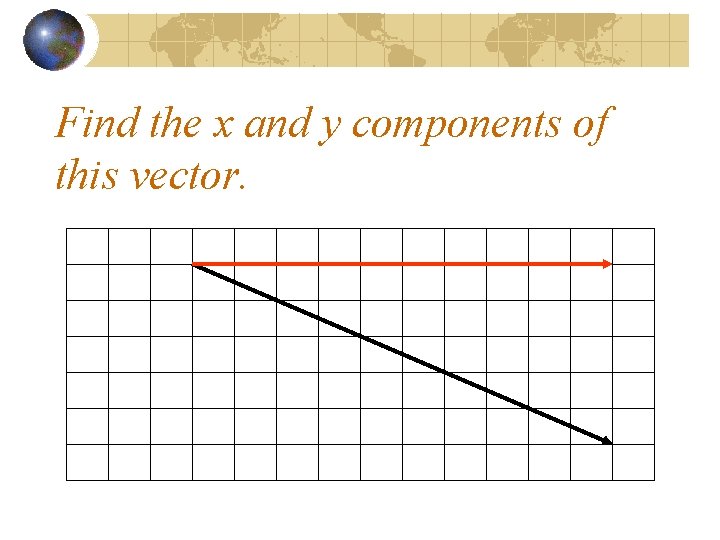
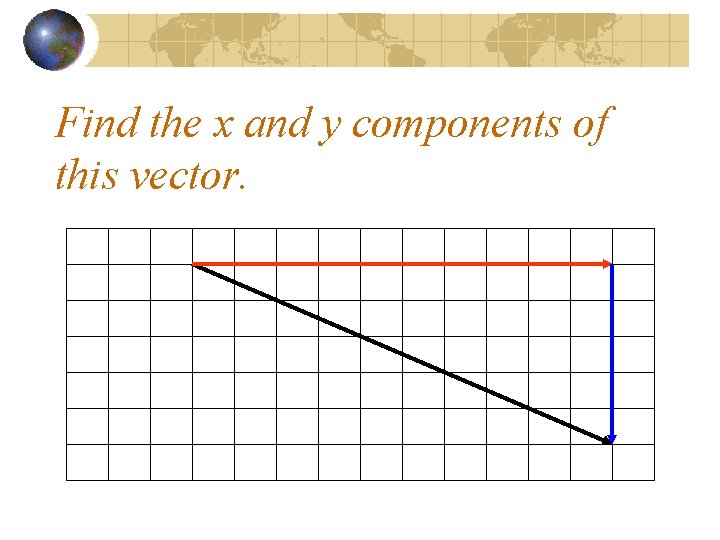
Find the x and y components of this vector.

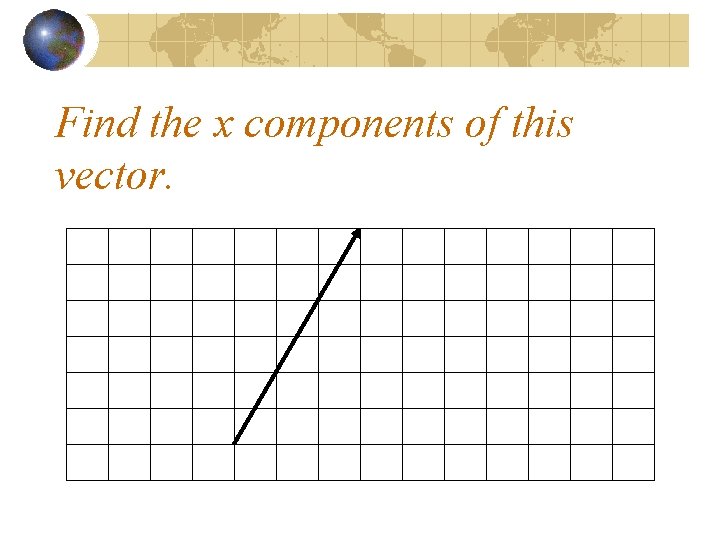
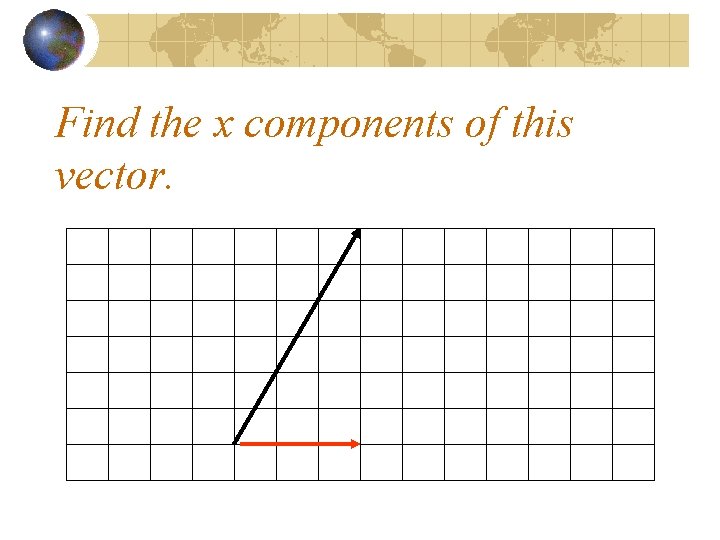
Find the x components of this vector.

Find the x components of this vector.

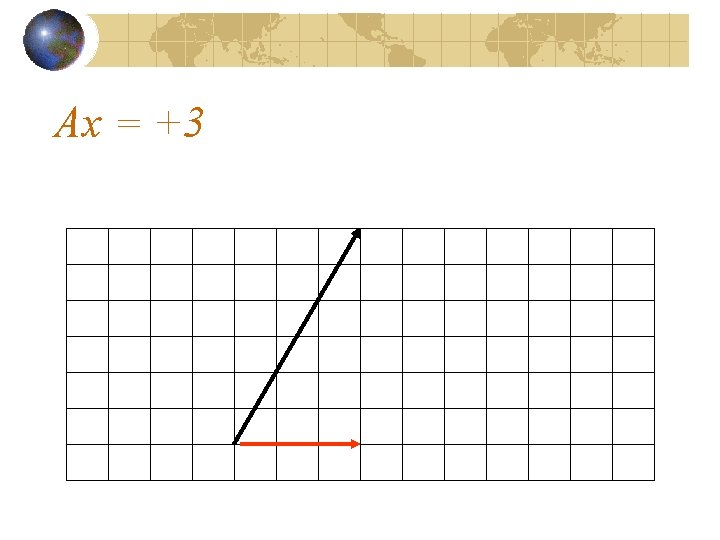
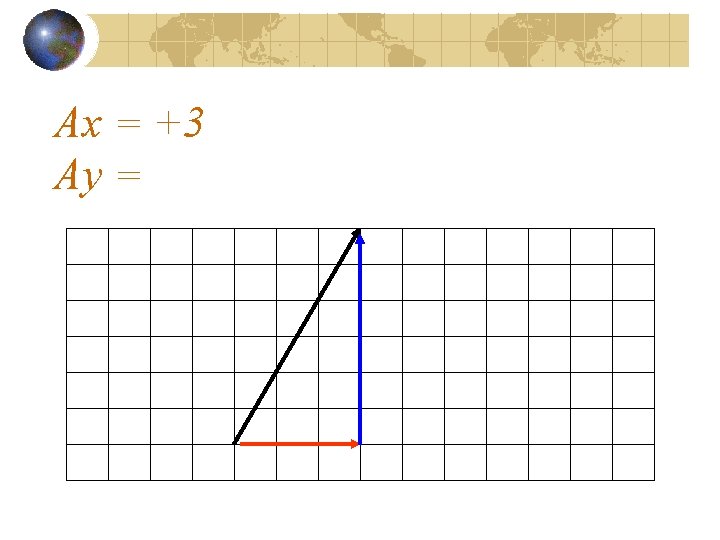
Ax = +3

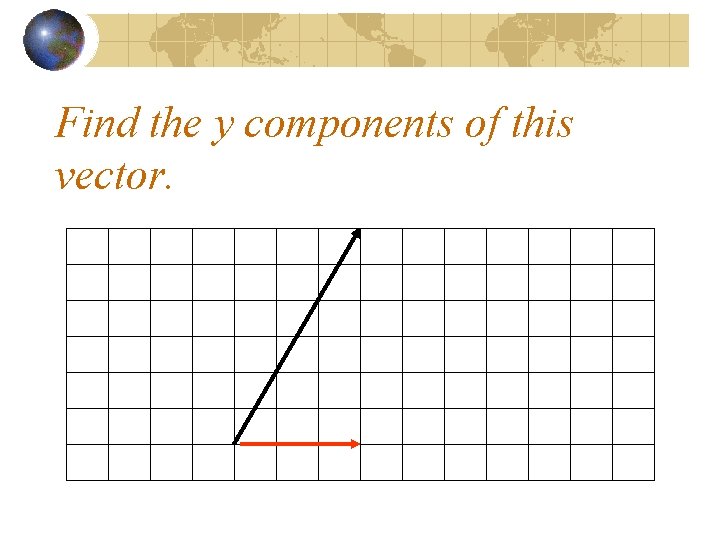
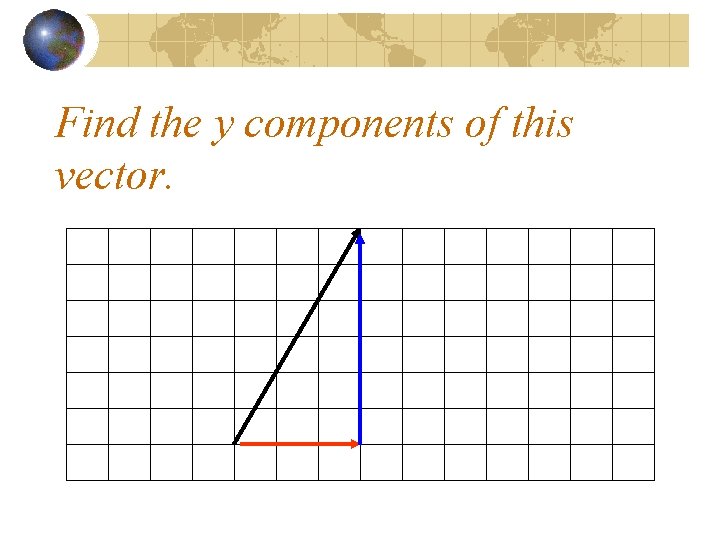
Find the y components of this vector.

Find the y components of this vector.

Ax = +3 Ay =

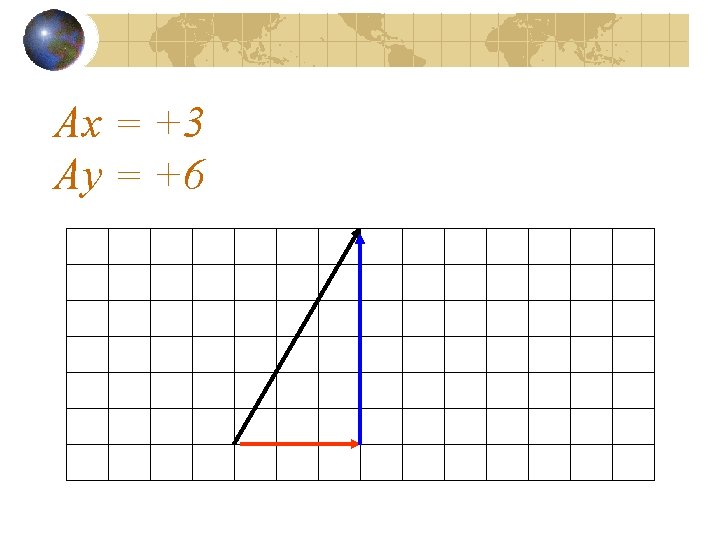
Ax = +3 Ay = +6

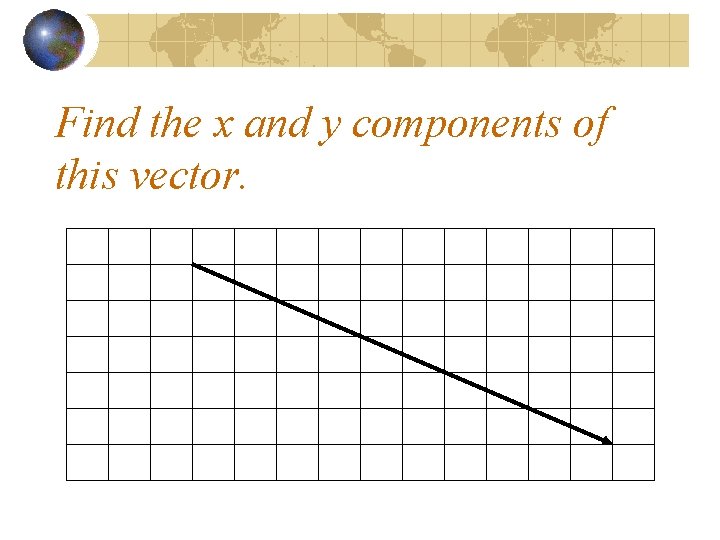
Find the x and y components of this vector.

Find the x and y components of this vector.

Find the x and y components of this vector.

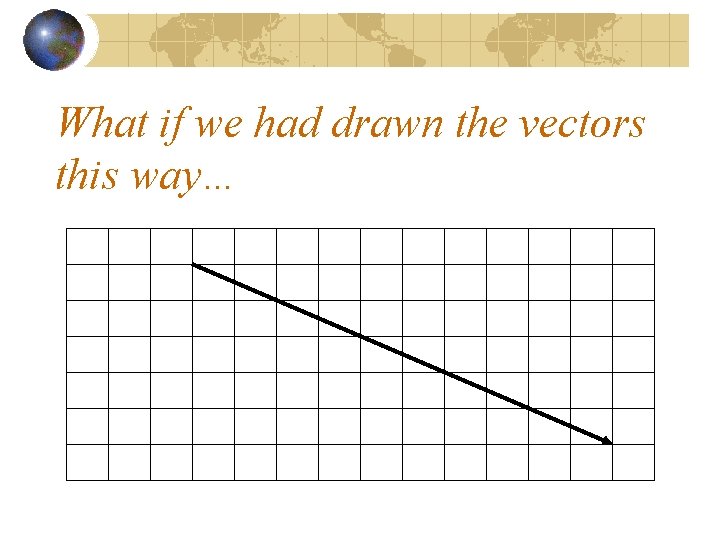
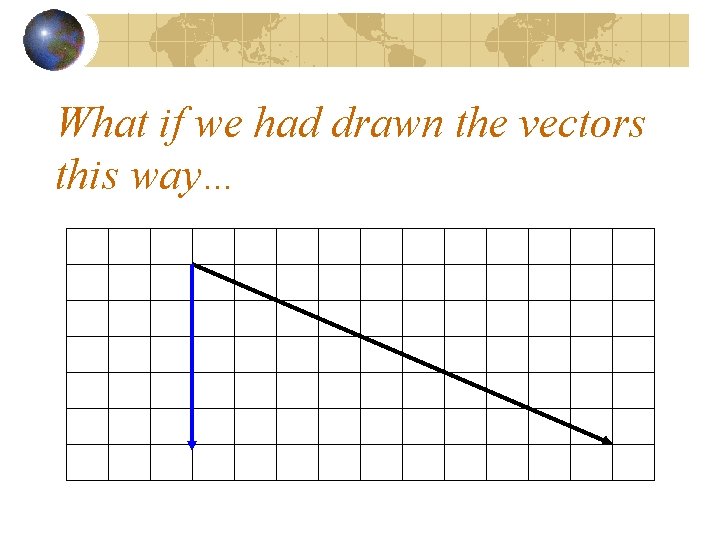
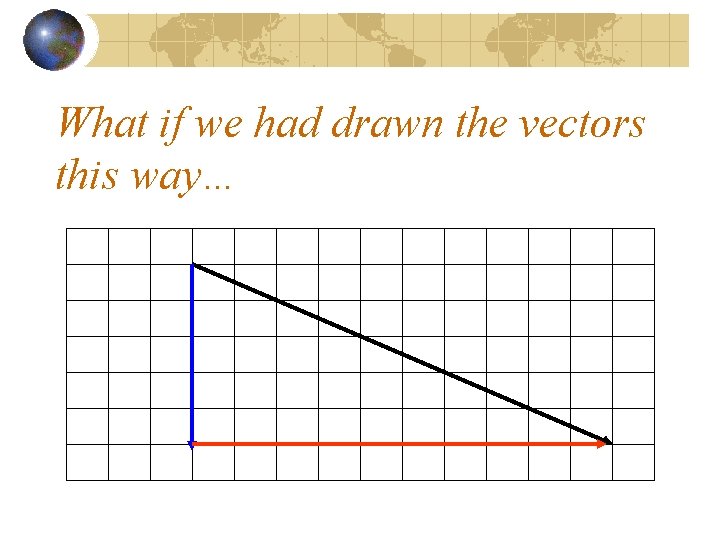
What if we had drawn the vectors this way…

What if we had drawn the vectors this way…

What if we had drawn the vectors this way…

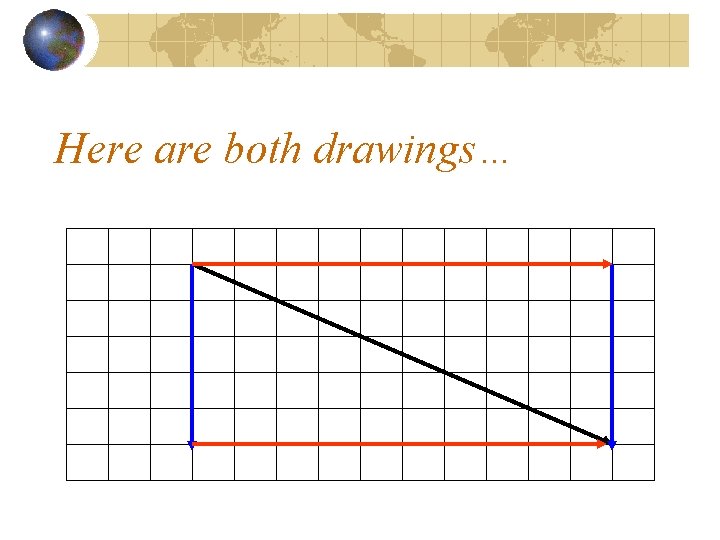
Here are both drawings…

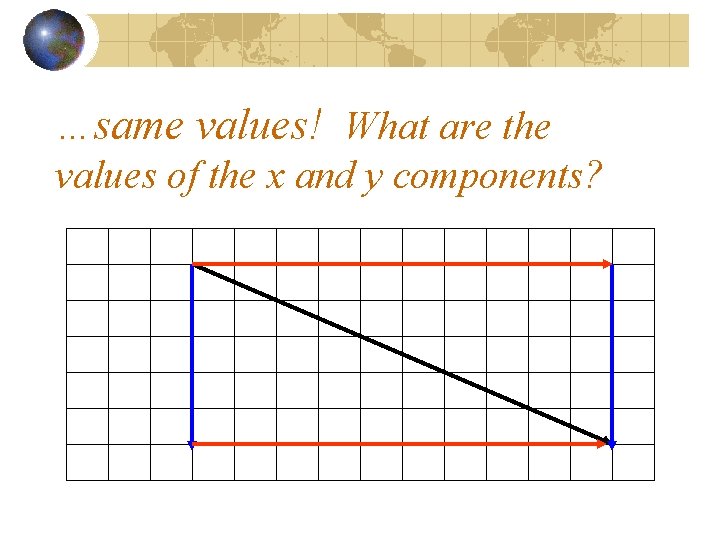
…same values! What are the values of the x and y components?

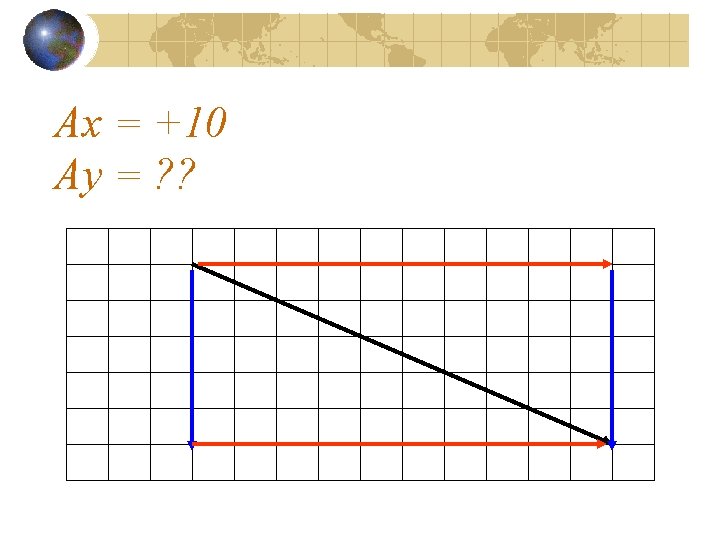
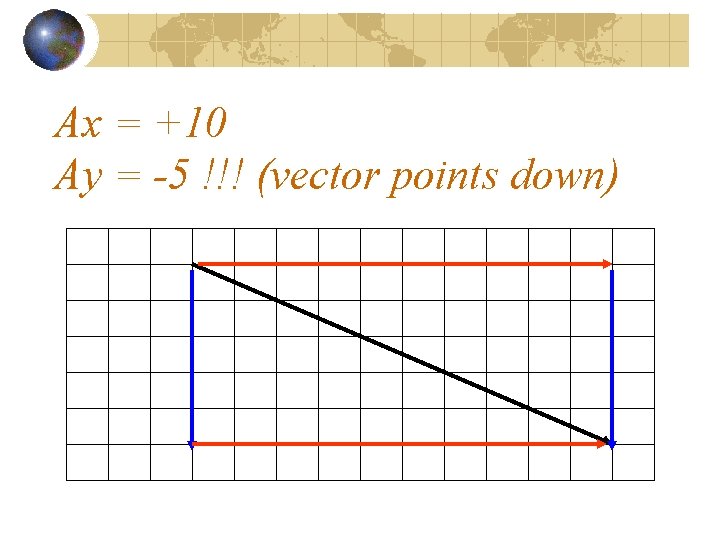
Ax = +10 Ay = ? ?

Ax = +10 Ay = -5 !!! (vector points down)

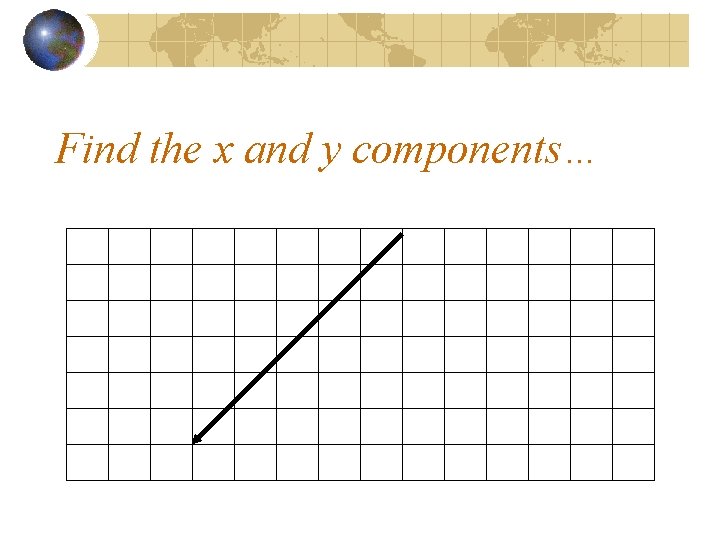
Find the x and y components…

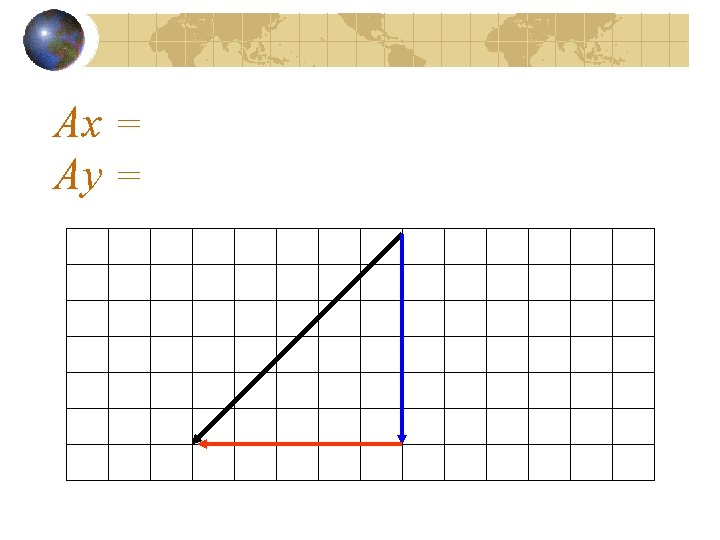
Ax = Ay =

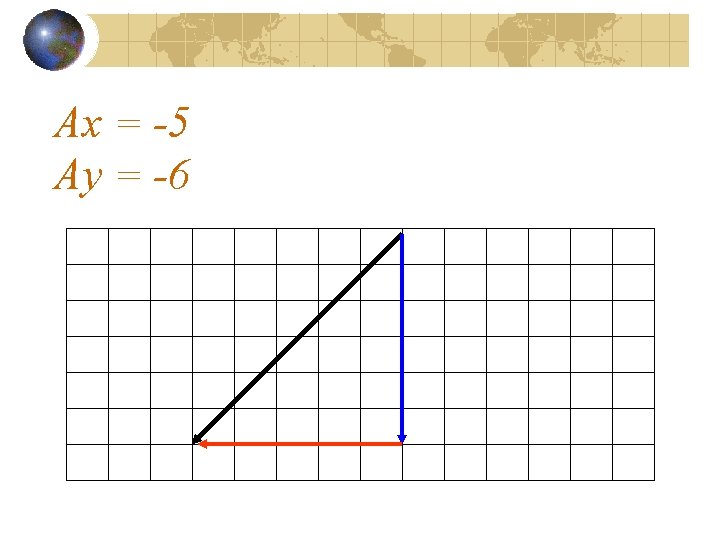
Ax = -5 Ay = -6

Find the x and y components of each vector

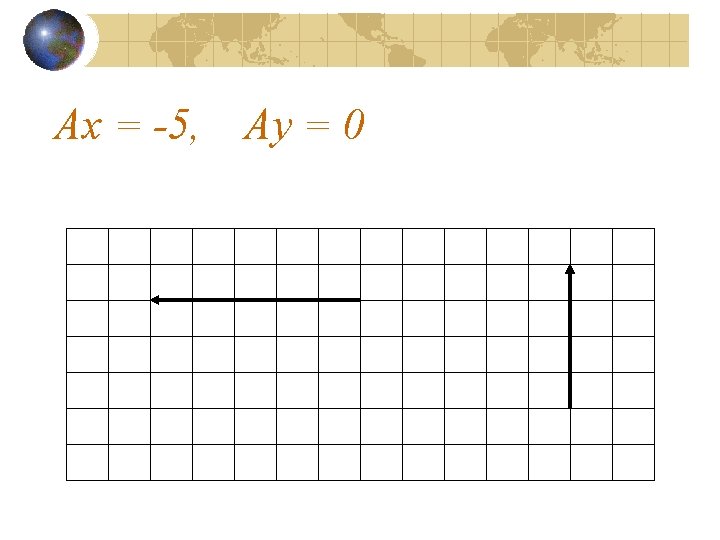
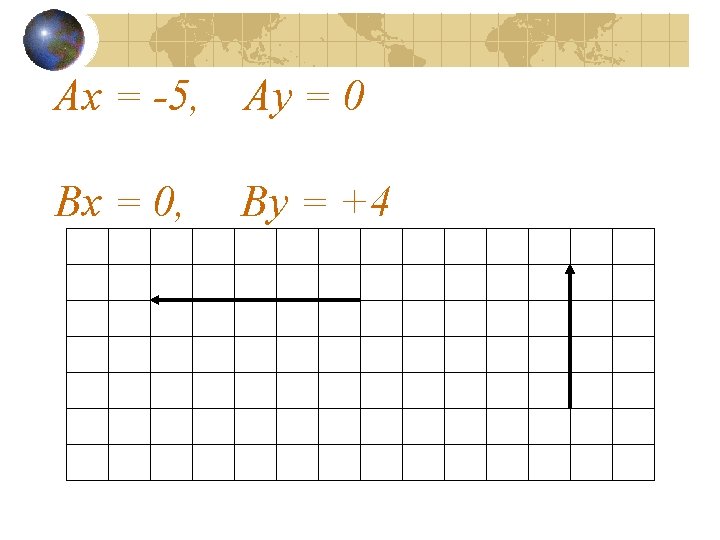
Ax = -5, Ay = 0

Ax = -5, Ay = 0 Bx = 0, By = +4

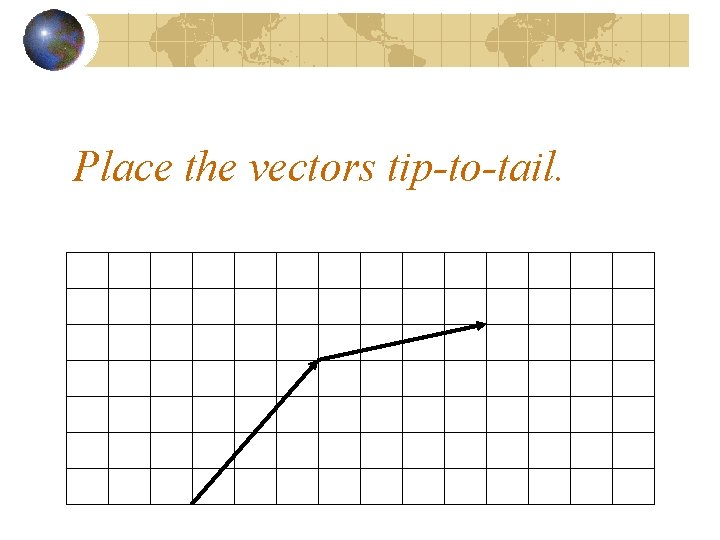
Let’s look at adding vectors using components. We’ll use the vectors below.

Place the vectors tip-to-tail.

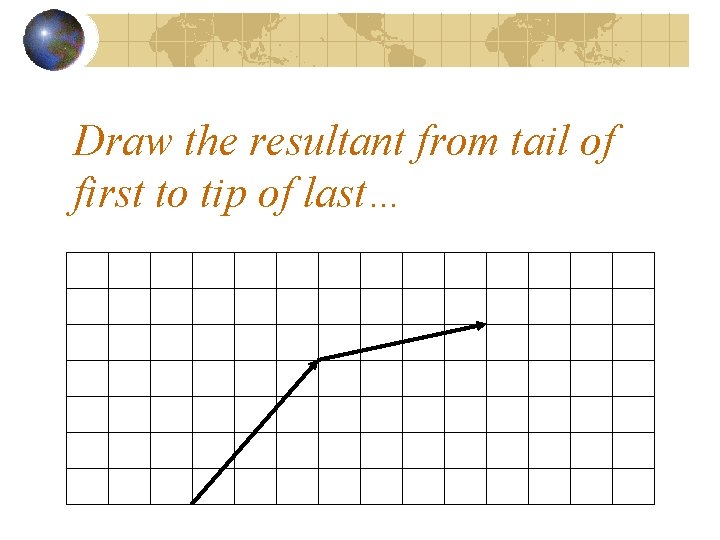
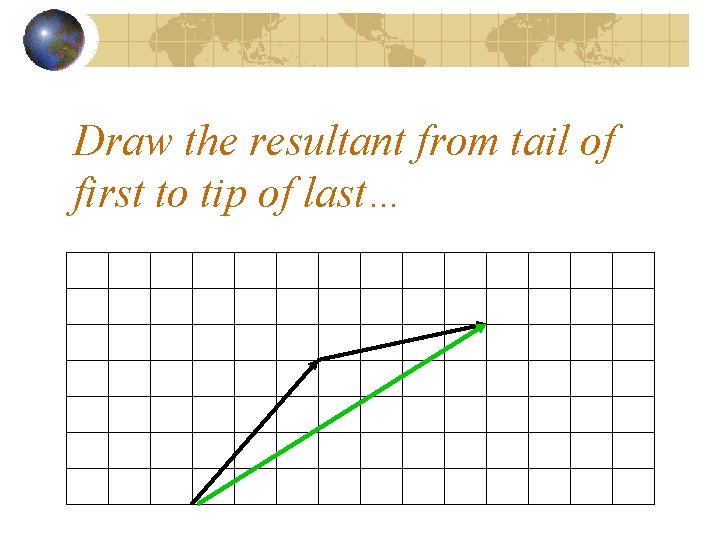
Draw the resultant from tail of first to tip of last…

Draw the resultant from tail of first to tip of last…

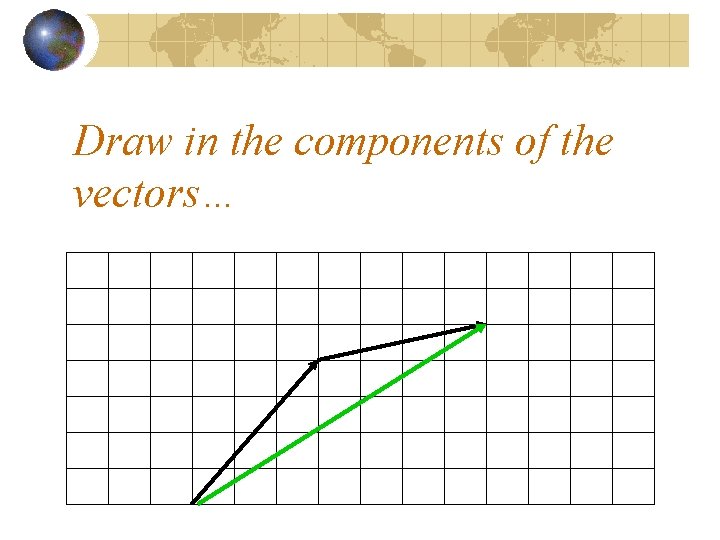
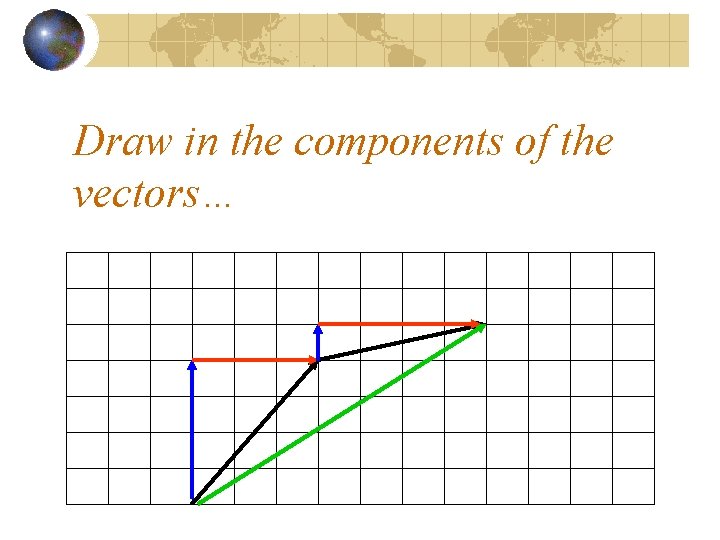
Draw in the components of the vectors…

Draw in the components of the vectors…

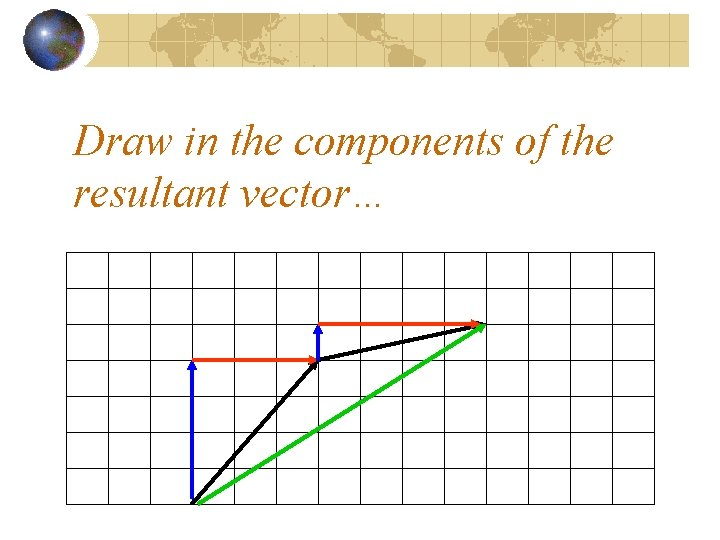
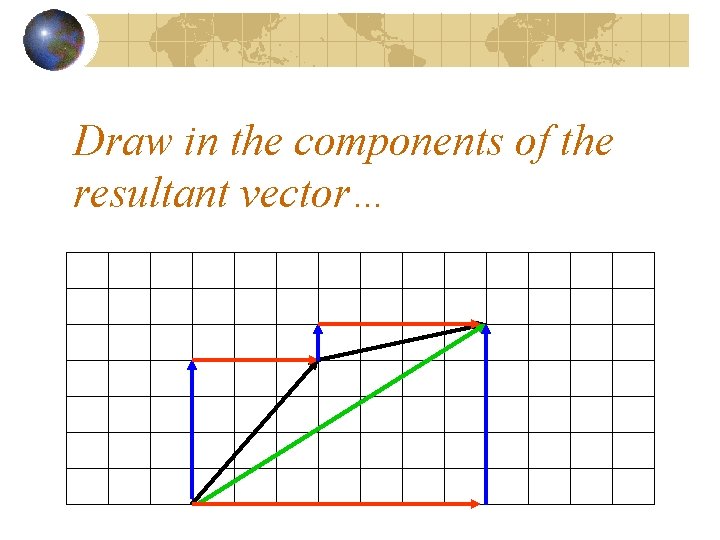
Draw in the components of the resultant vector…

Draw in the components of the resultant vector…

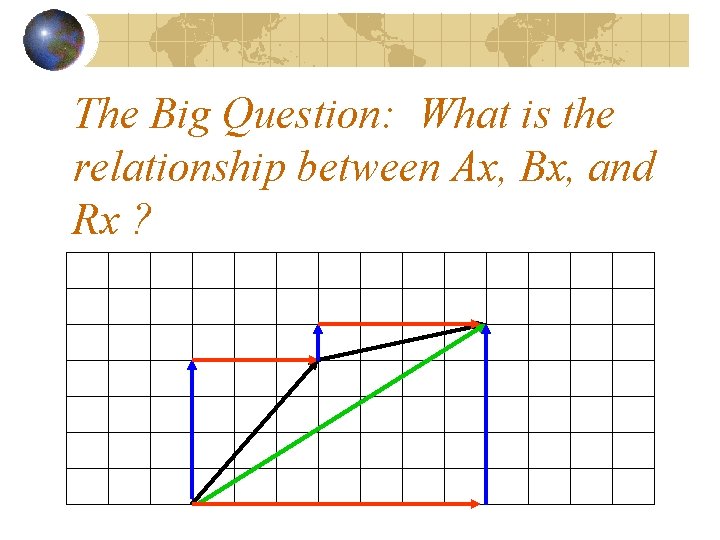
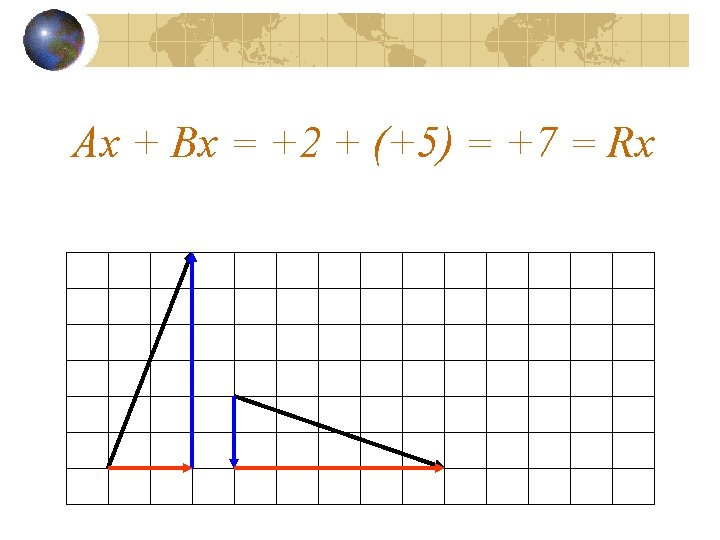
The Big Question: What is the relationship between Ax, Bx, and Rx ?

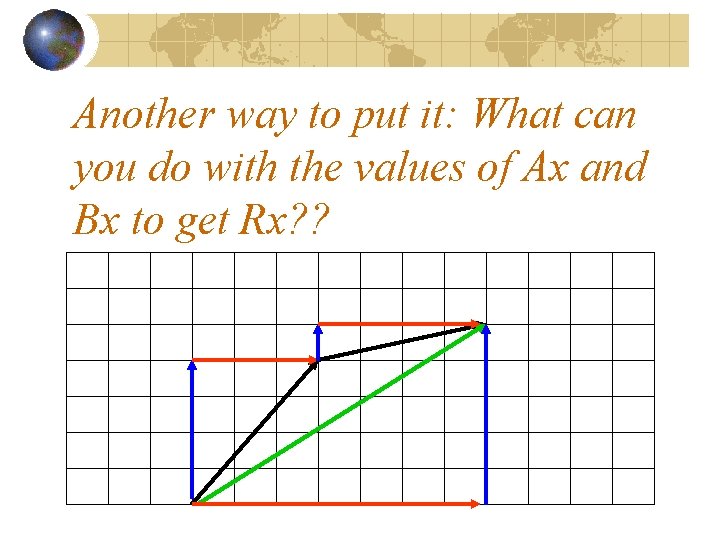
Another way to put it: What can you do with the values of Ax and Bx to get Rx? ?

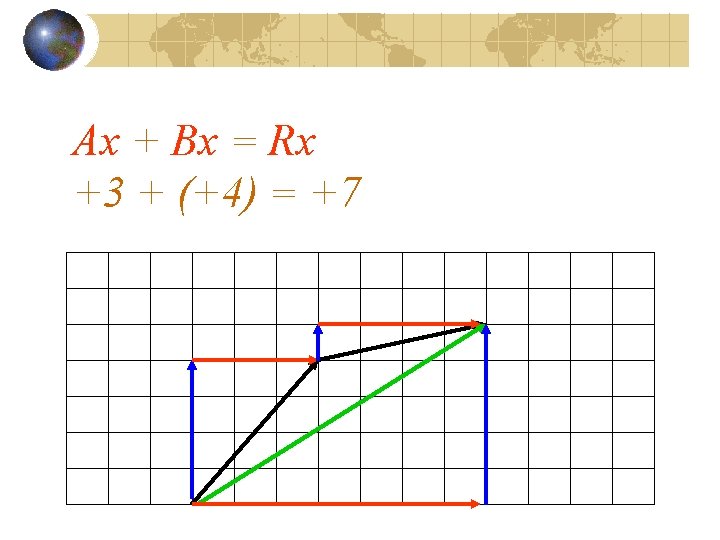
Ax + Bx = Rx +3 + (+4) = +7

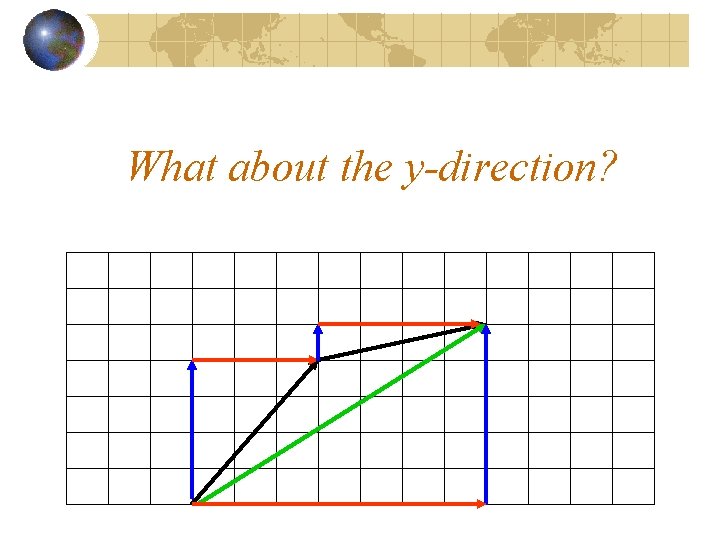
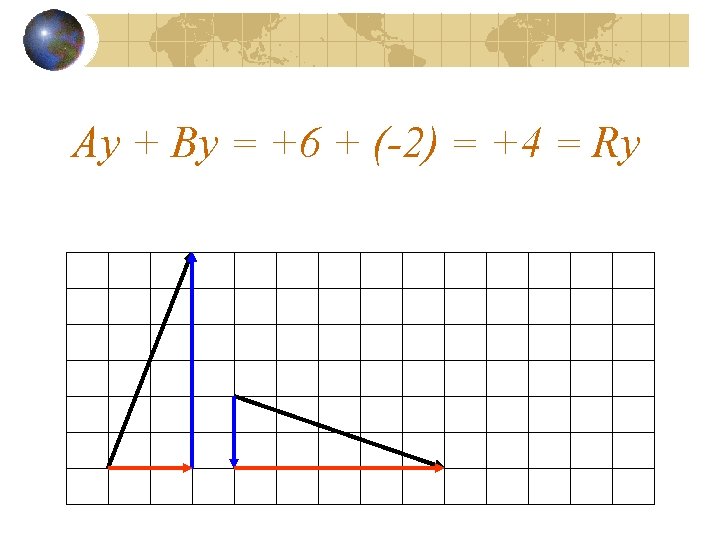
What about the y-direction?

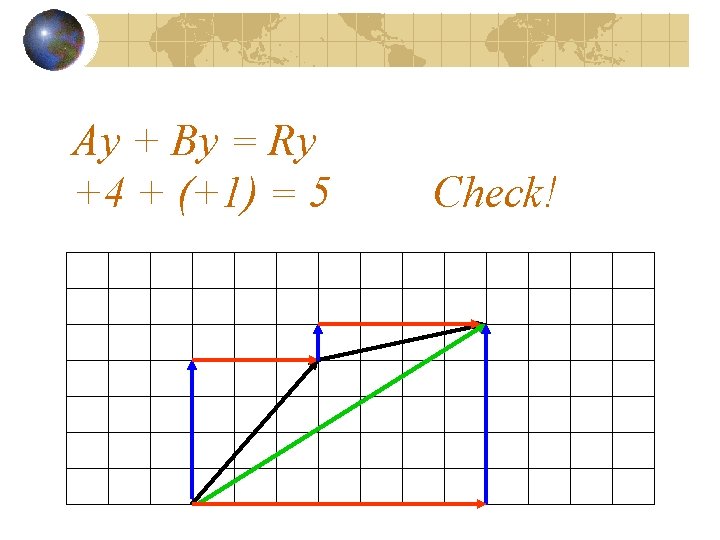
Ay + By = Ry +4 + (+1) = 5 Check!

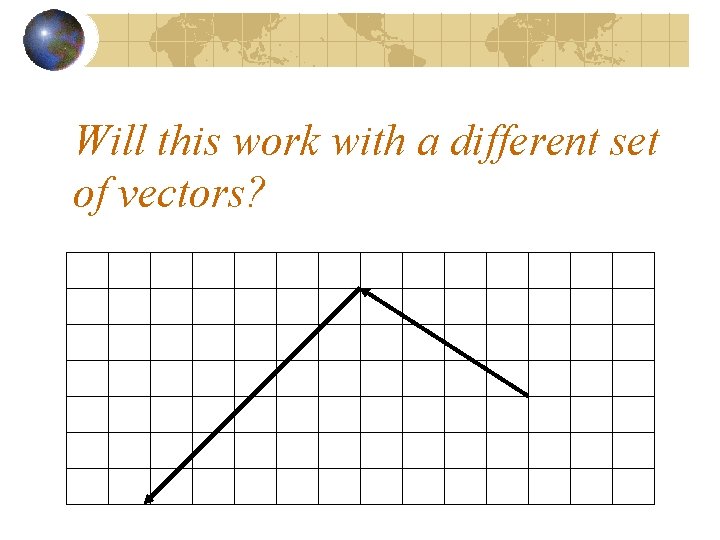
Will this work with a different set of vectors?

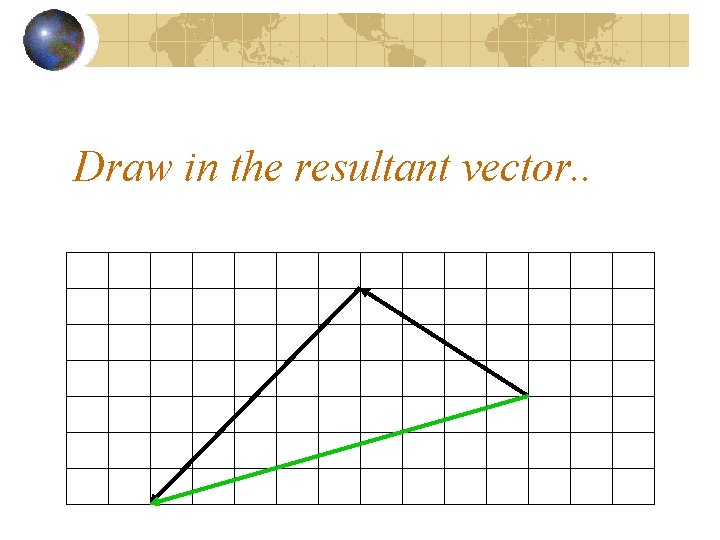
Draw in the resultant vector. .

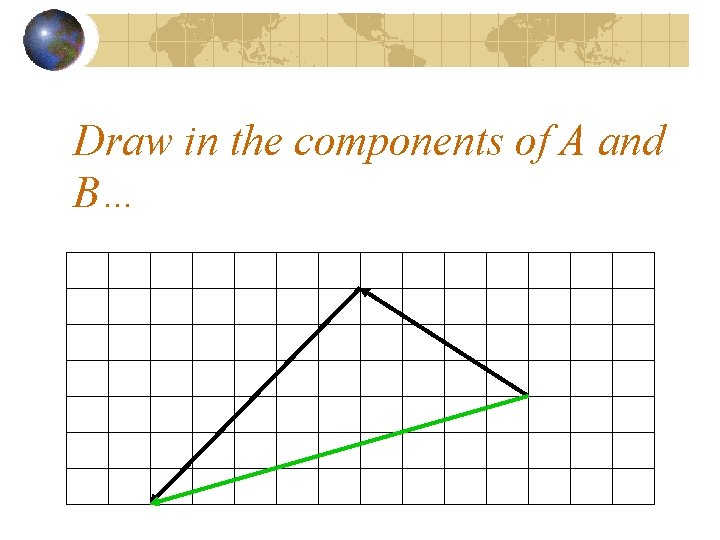
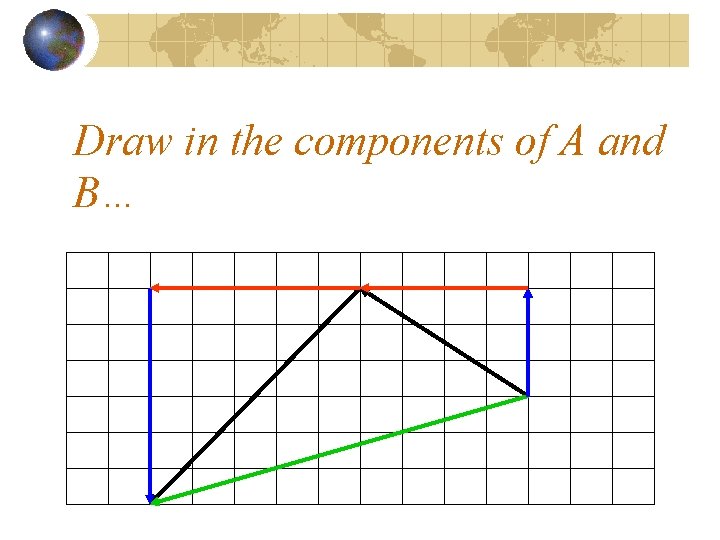
Draw in the components of A and B…

Draw in the components of A and B…

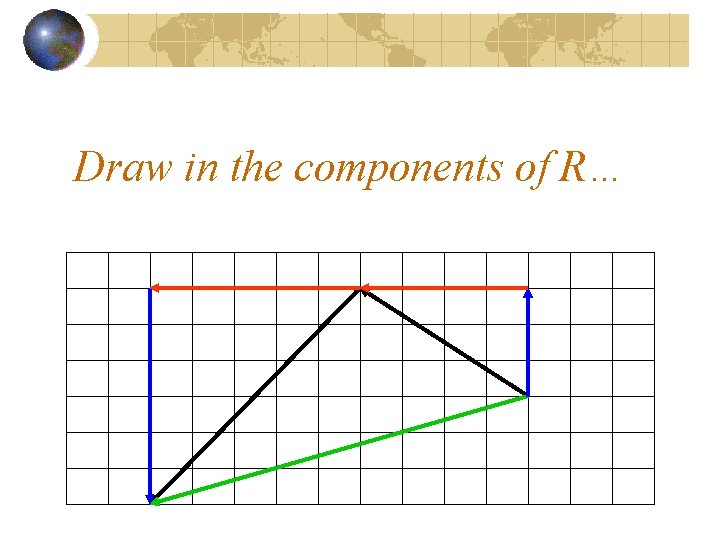
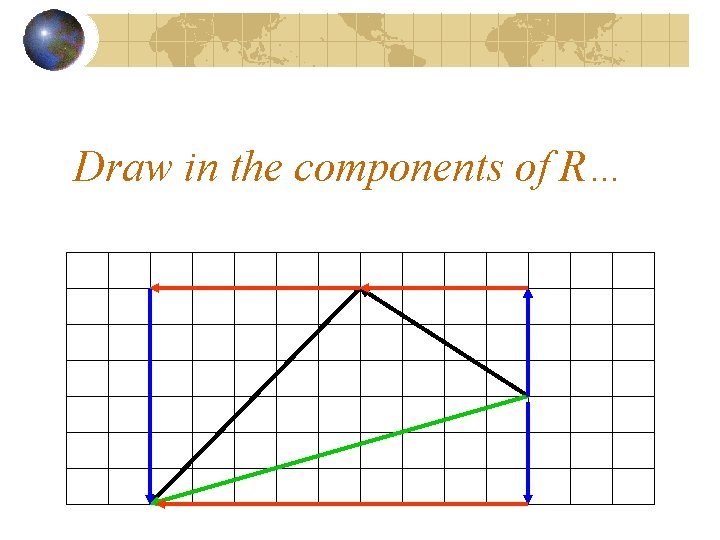
Draw in the components of R…

Draw in the components of R…

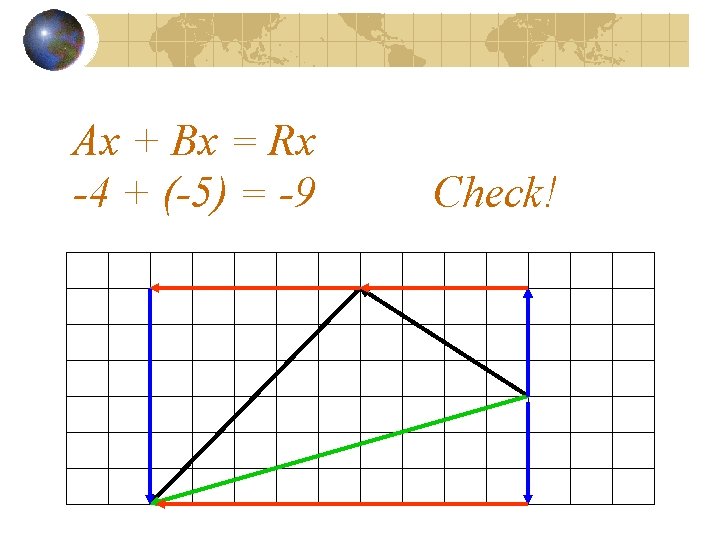
Will our previous recipe work? (Ax + Bx = Rx)

Ax + Bx = Rx -4 + (-5) = -9 Check!

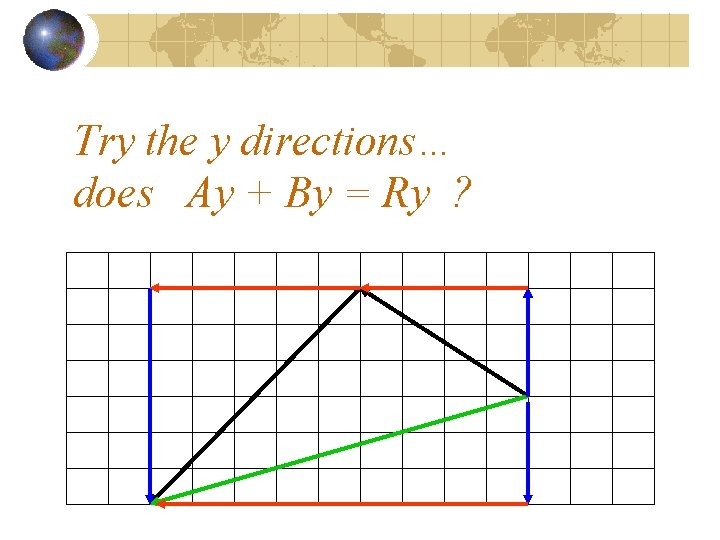
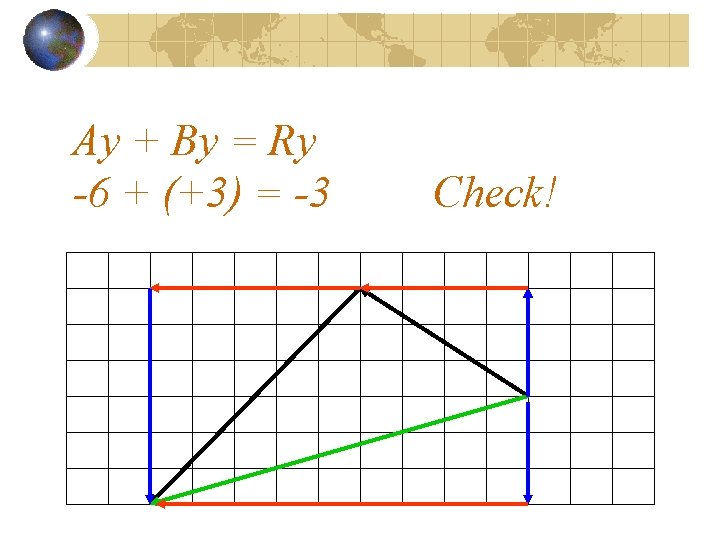
Try the y directions… does Ay + By = Ry ?

Ay + By = Ry -6 + (+3) = -3 Check!

Why does this help?

There are Two Reasons: 1. You can determine the resultant vector without having to draw each of the vectors 2. You can get much more accurate results if you use math – specifically, the Pythagorean theorem

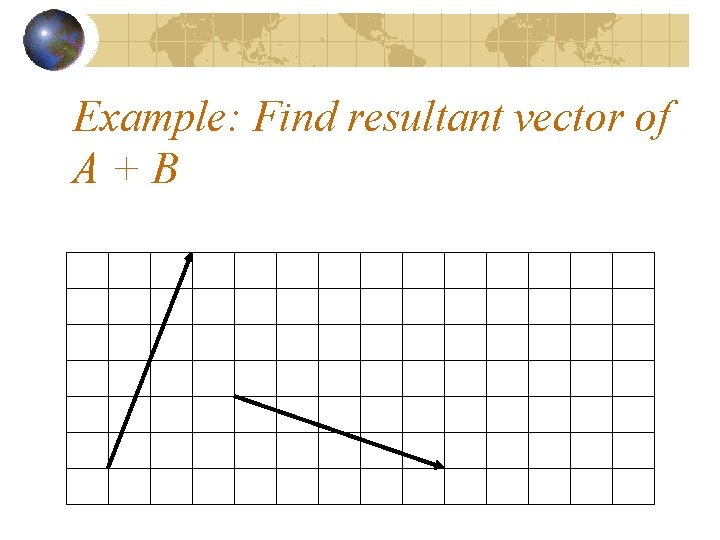
Example: Find resultant vector of A+B

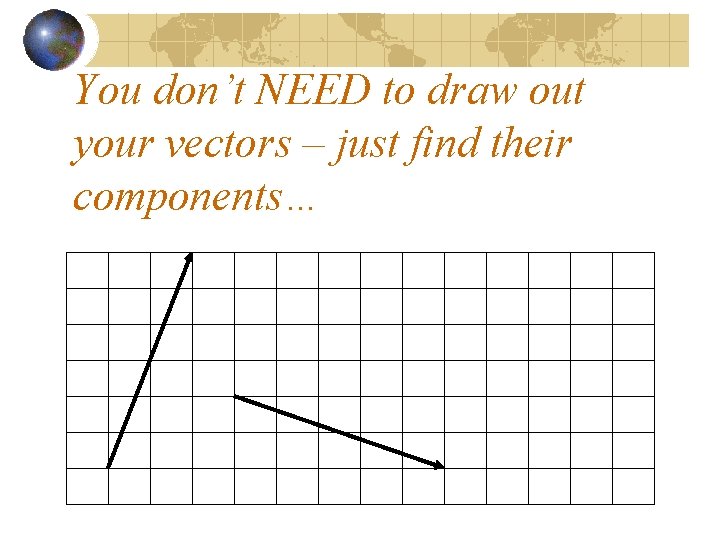
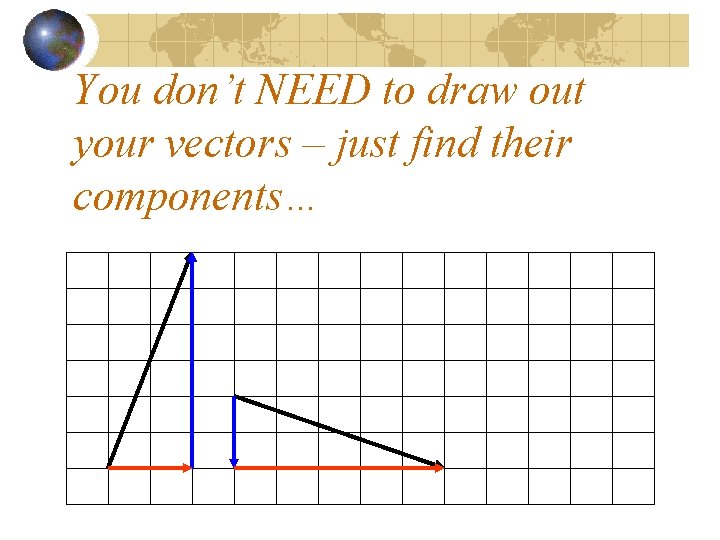
You don’t NEED to draw out your vectors – just find their components…

You don’t NEED to draw out your vectors – just find their components…

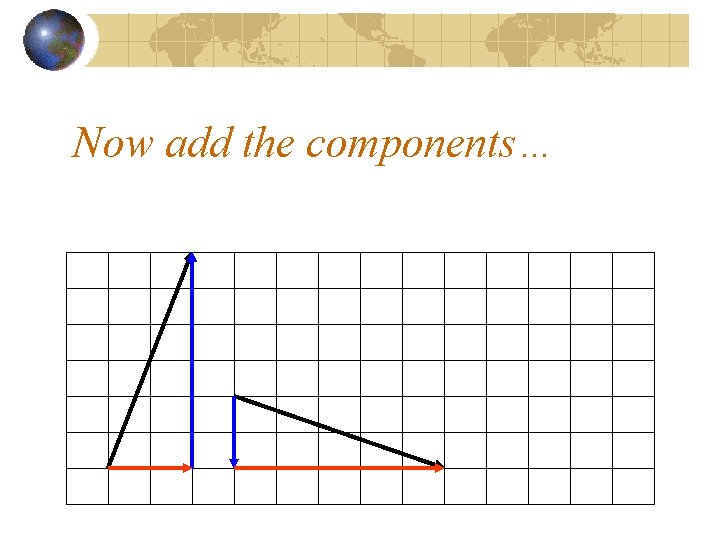
Now add the components…

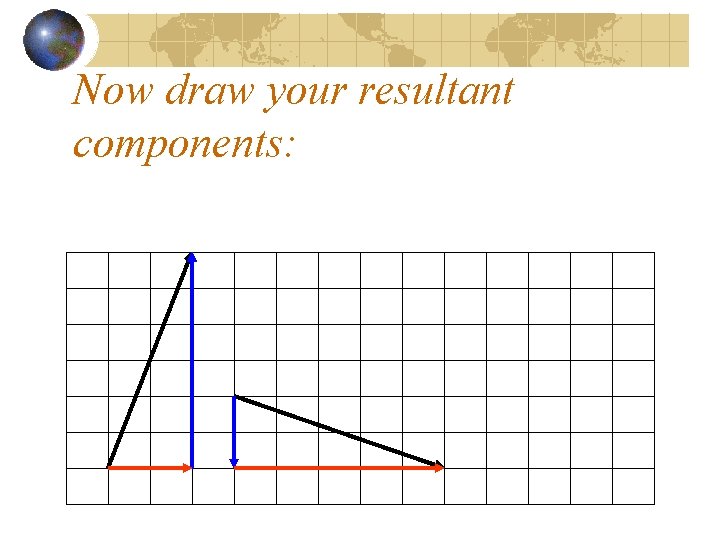
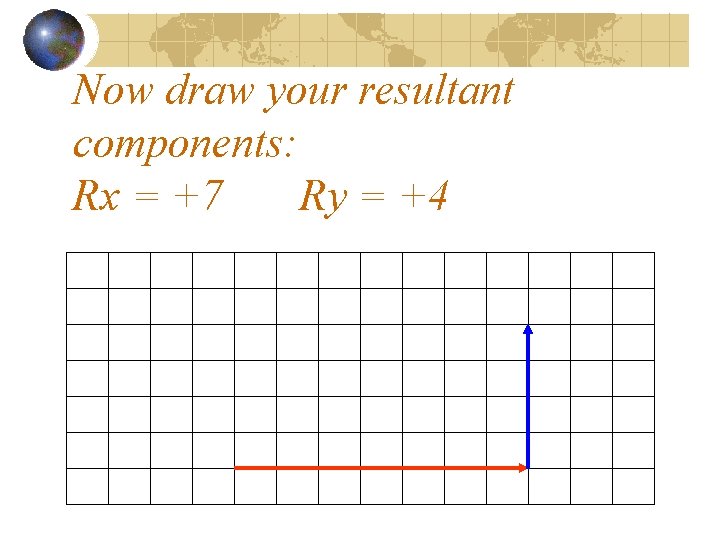
Now draw your resultant components:

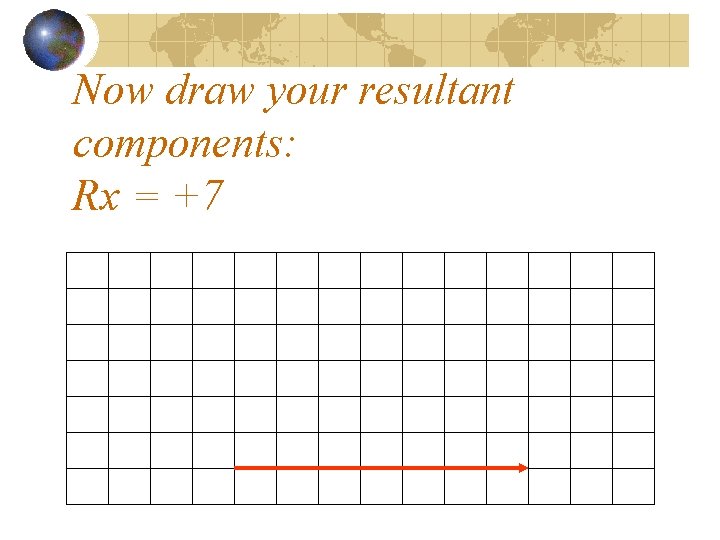
Now draw your resultant components: Rx = +7

Now draw your resultant components: Rx = +7 Ry = +4

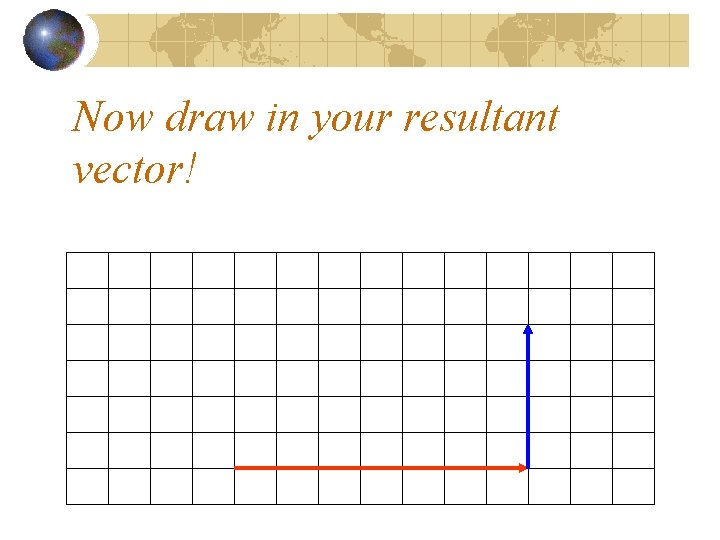
Now draw in your resultant vector!

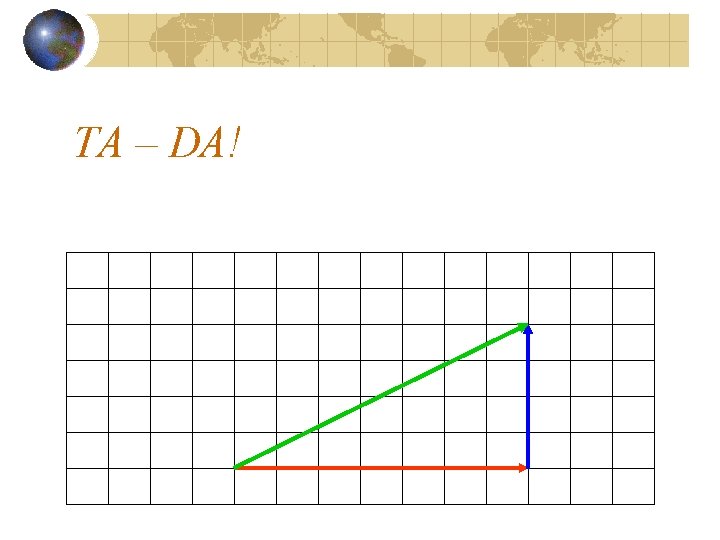
TA – DA!