Components of a Mathematical Model Governing Equation Boundary

Components of a Mathematical Model • Governing Equation • Boundary Conditions • Initial conditions (for transient problems) In full solute transport problems, we have two mathematical models: one for flow and one for transport. The governing equation for solute transport problems is the advection-dispersion equation.

Conceptual Model A descriptive representation of a groundwater system that incorporates an interpretation of the geological, hydrological, and geochemical conditions, including information about the boundaries of the problem domain.

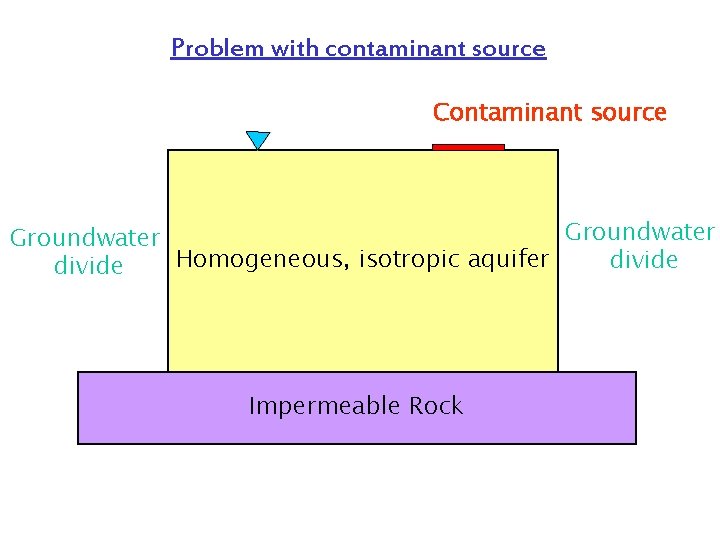
Problem with contaminant source Contaminant source Groundwater Homogeneous, isotropic aquifer divide Impermeable Rock 2 D, steady state

Processes to model 1. Groundwater flow 2. Transport (a) Particle tracking: requires velocities and a particle tracking code. calculate path lines (b) Full solute transport: requires velocities and a solute transport model. calculate concentrations

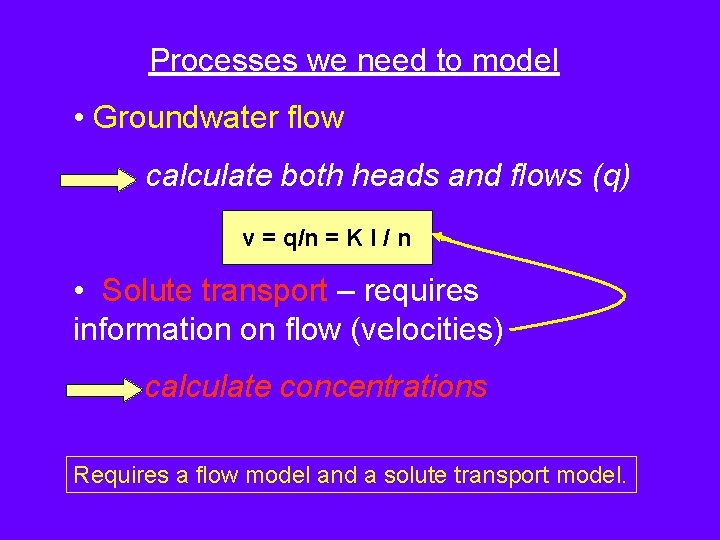
Processes we need to model • Groundwater flow calculate both heads and flows (q) v = q/n = K I / n • Solute transport – requires information on flow (velocities) calculate concentrations Requires a flow model and a solute transport model.

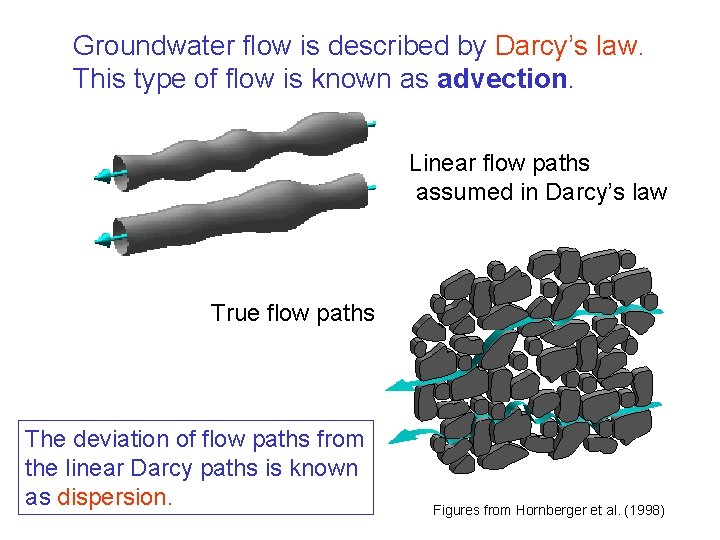
Groundwater flow is described by Darcy’s law. This type of flow is known as advection. Linear flow paths assumed in Darcy’s law True flow paths The deviation of flow paths from the linear Darcy paths is known as dispersion. Figures from Hornberger et al. (1998)

In addition to advection, we need to consider two other processes in transport problems. • Dispersion • Chemical reactions Advection-dispersion equation with chemical reaction terms.

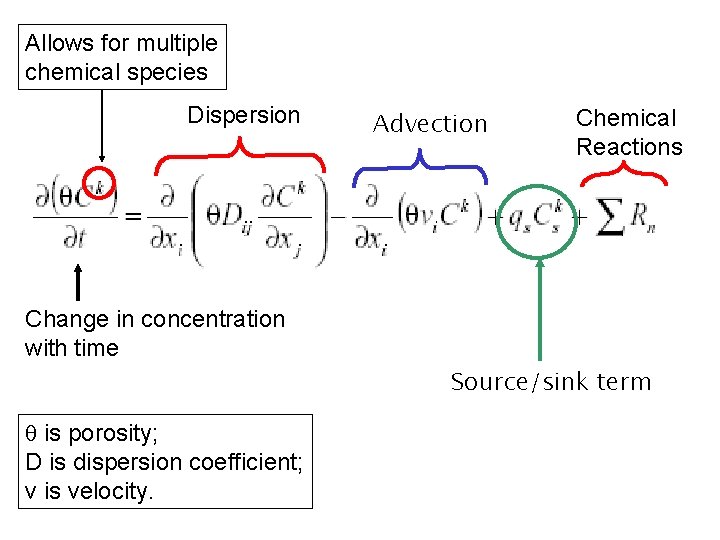
Allows for multiple chemical species Dispersion Advection Chemical Reactions Change in concentration with time Source/sink term q is porosity; D is dispersion coefficient; v is velocity.

advection-dispersion equation groundwater flow equation

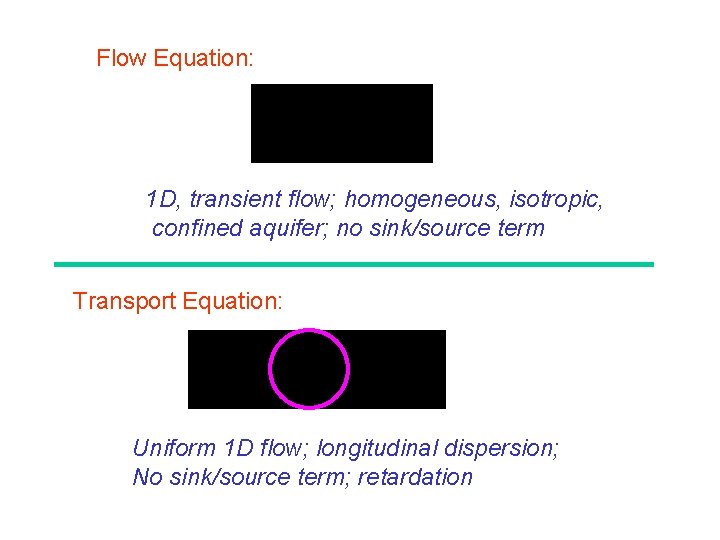
Flow Equation: 1 D, transient flow; homogeneous, isotropic, confined aquifer; no sink/source term Transport Equation: Uniform 1 D flow; longitudinal dispersion; No sink/source term; retardation

Models Parameters • Initial Concentration: Page 224 • Dispersion: Page 227/228