Componenti fortemente connesse Componenti fortemente connesse Una componente

Componenti fortemente connesse

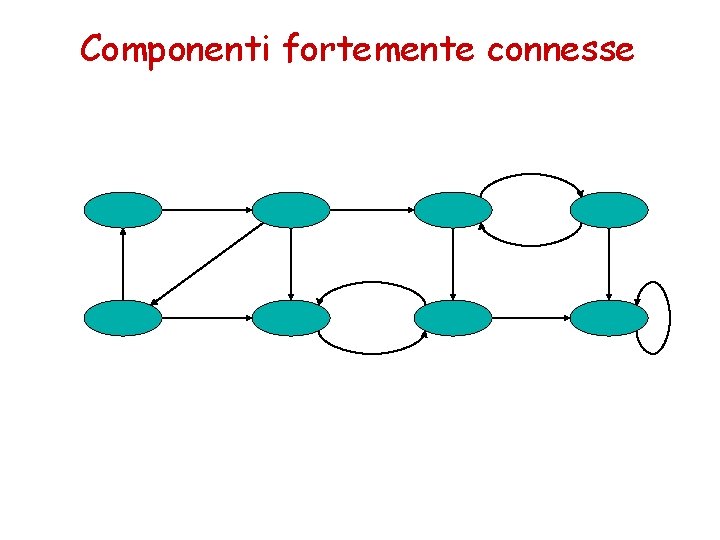
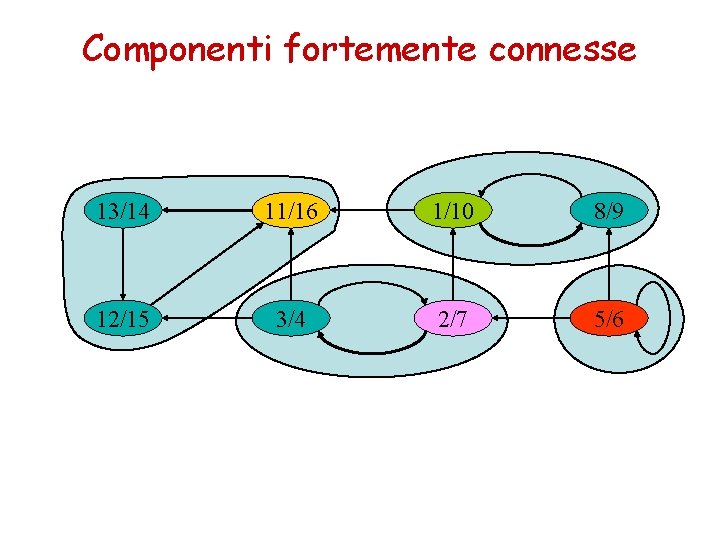
Componenti fortemente connesse Una componente fortemente connessa (CFC) di un grafo orientato G=(V, E) è un insieme massimale di vertici U V tale che per ogni coppia di vertici u e v in U si ha che ciascuno dei due vertici è raggiungibile dall’altro.

Componenti fortemente connesse

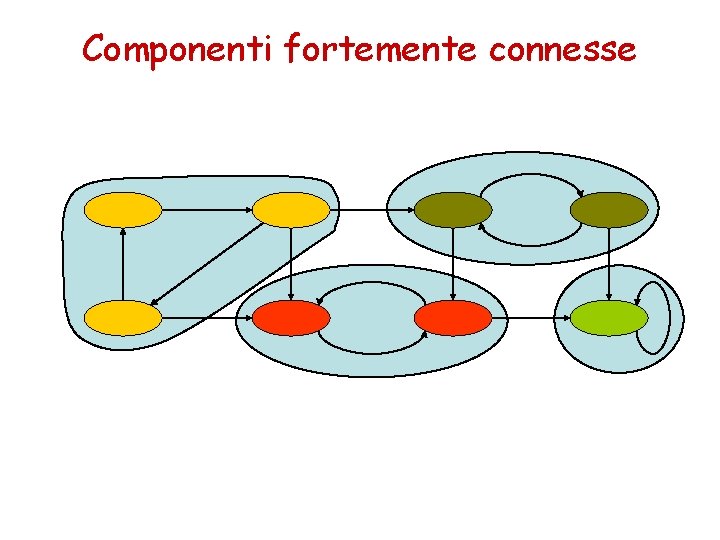
Componenti fortemente connesse

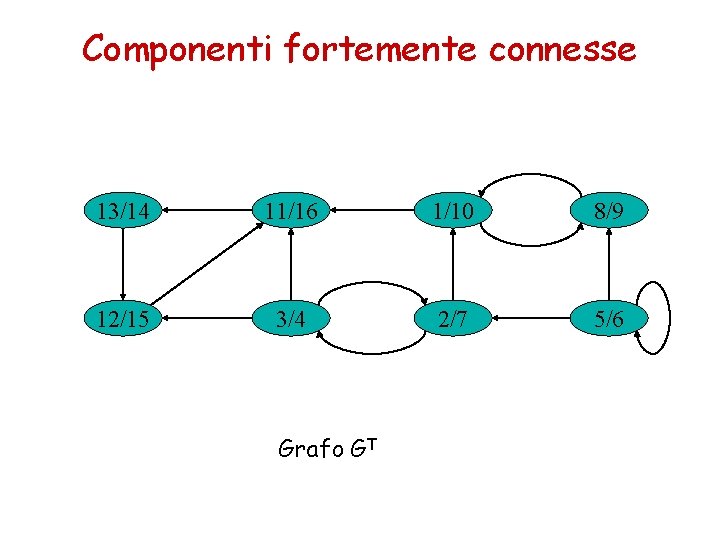
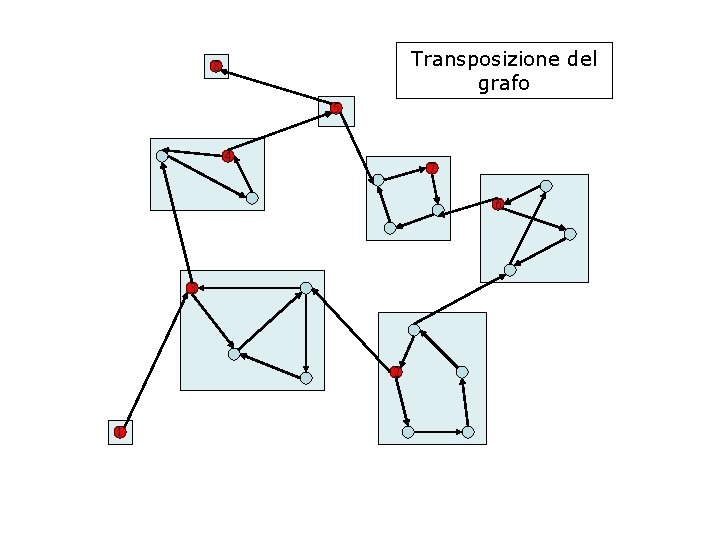
Grafo trasposto Il grafo GT=(V, ET) è il trasposto di G=(V, E) se ET = {(u, v): (v, u) E} (rovescia il senso di percorrenza degli archi di G). G e GT hanno le stesse componenti fortemente connesse.

Componenti fortemente connesse L’algoritmo seguente trova in tempo lineare (O(V+E)) le componenti connesse di un grafo orientato G=(V, E). Strongly-Connected-Components(G) 1. chiama DFS(G) per calcolare f[u] per ogni vertice u 2. calcola GT 3. chiama DFS(GT), ma nel ciclo principale di DFS considera i vertici in ordine decrescente di f[u] 4. return i vertici di ogni albero nella foresta DFS prodotta al passo 3 come una diversa componente fortemente connessa

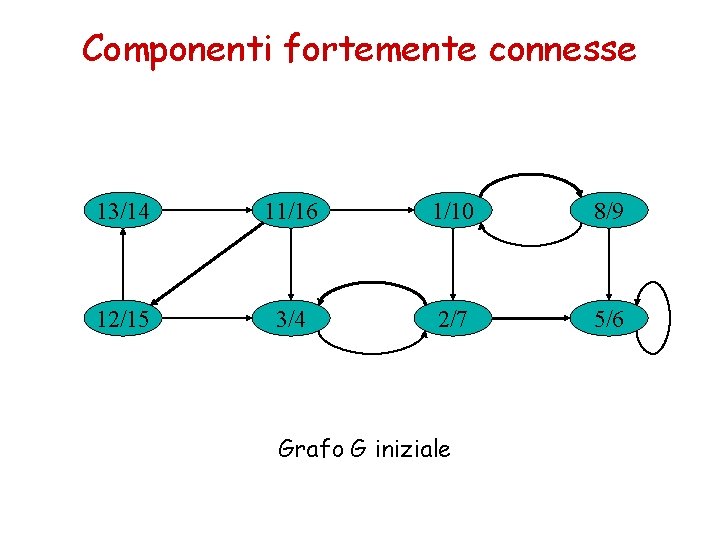
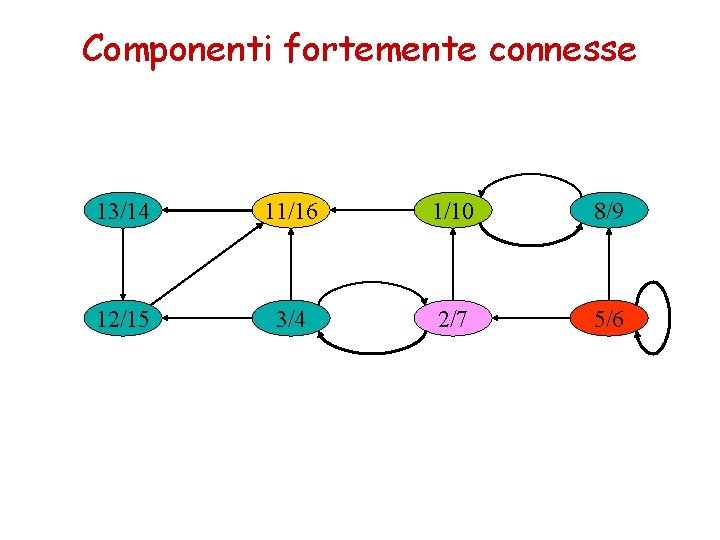
Componenti fortemente connesse 13/14 11/16 1/10 8/9 12/15 3/4 2/7 5/6 Grafo G iniziale

Componenti fortemente connesse 13/14 11/16 1/10 8/9 12/15 3/4 2/7 5/6 Grafo GT

Componenti fortemente connesse 13/14 11/16 1/10 8/9 12/15 3/4 2/7 5/6

Componenti fortemente connesse 13/14 11/16 1/10 8/9 12/15 3/4 2/7 5/6

Componenti fortemente connesse Lemma Se due vertici sono nella stessa CFC, allora nessun cammino fra loro esce da questa CFC. Teorema In una qualunque visita in profondità, tutti i vertici in una stessa CFC sono posti nello stesso albero DFS.

Avi Un avo (u) di un vertice u è il vertice (unico) w raggiungibile da u che massimizza f[w] (w è l’ultimo nodo raggiungibile da u nell’ordinamento della DFS). Teorema In un grafo orientato G = (V, E) l’avo (u) di un qualunque vertice u V in una qualunque visita in profondità di G è un antenato di u.

Componenti fortemente connesse Corollario In ogni visita in profondità di un grafo orientato G = (V, E), per ogni vertice u V i vertici u e (u) appartengono alla stessa CFC. Teorema In un grafo orientato G = (V, E), due vertici u, v V appartengono alla stessa CFC se e solo se essi hanno lo stesso avo in una visita in profondità di G.

Correttezza Teorema Strongly-Connected-Components(G) calcola correttamente le CFC di un grafo orientato G. Dim. Per induzione. Tesi: se tutti gli alberi prodotti prima dell’n-esimo nella DFS sono CFC, allora lo è anche l’n-esimo. Banalmente vero per n=0. Per il caso induttivo, cont. . .

Considera un albero DFS, T con radice r prodotto dalla ricerca per profondità su GT, sia C(r) l’insieme dei vertici con avo r. Tesi: un vertice u è presente in T, sse u è in C(r). Chiaramente, ogni vertice in C(r) è anche in T. Se f[ (w)]>f[r], allora w non può essere in C(r): – Quando r viene selezionato, w è già stato inserito nell’albero con radice (w). Se f[ (w)]<f[r], allora w non può essere in C(r): – Se w fosse in C( r), allora r sarebbe raggiungibile da w. Quindi r f[r]<f[ (w)]

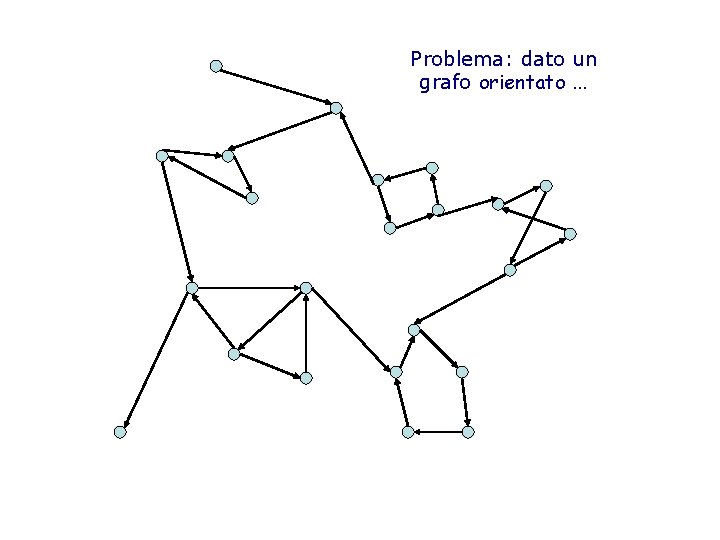
Problema: dato un grafo orientato …

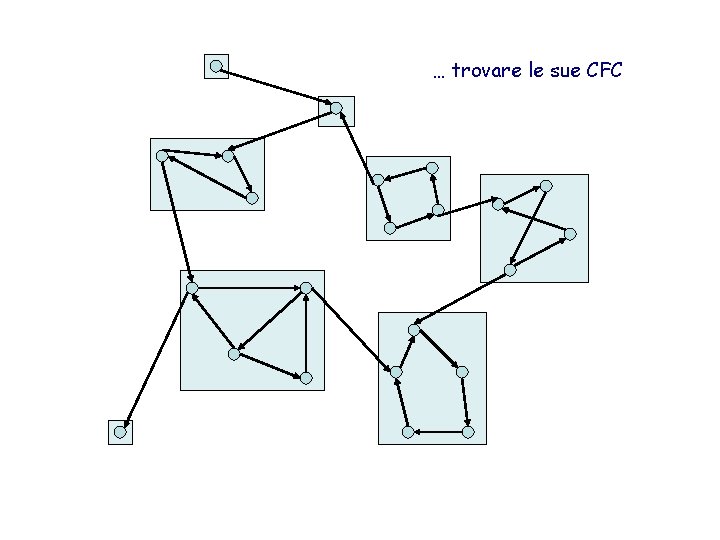
… trovare le sue CFC

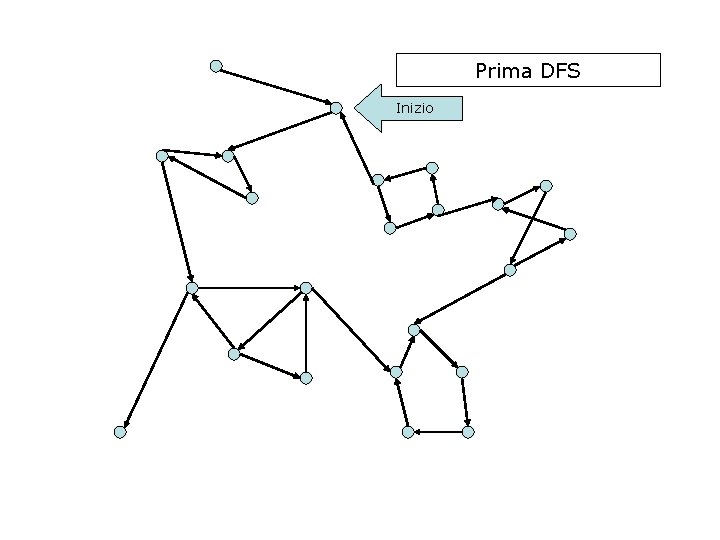
Prima DFS Inizio

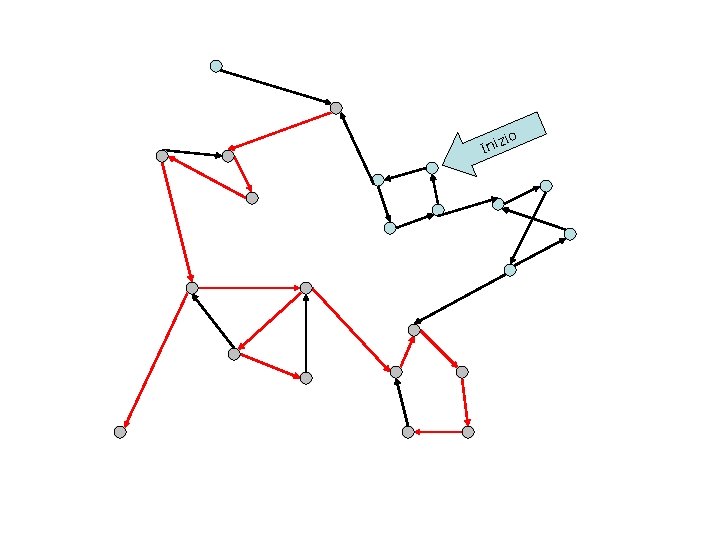
zio Ini

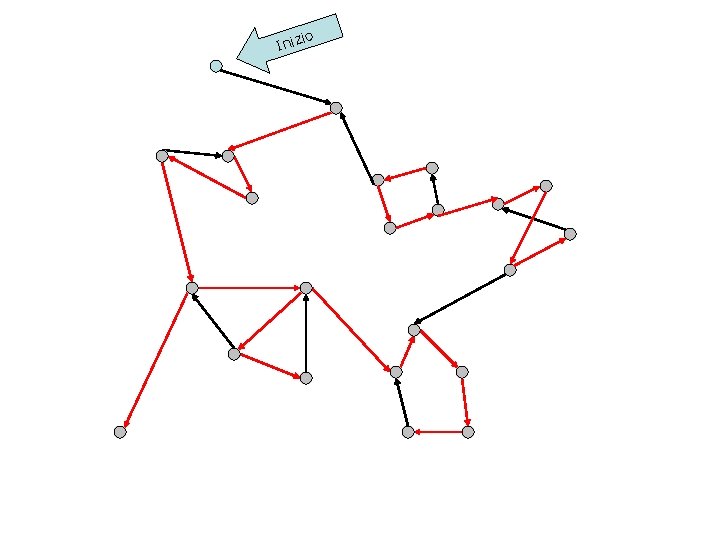
io Iniz

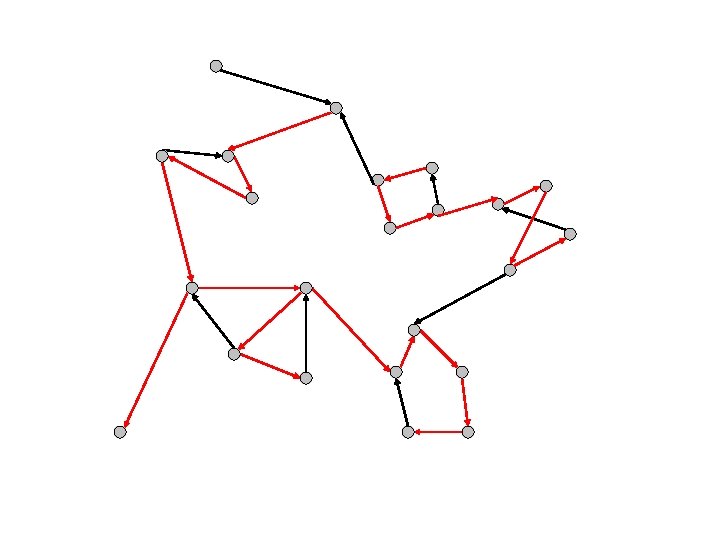
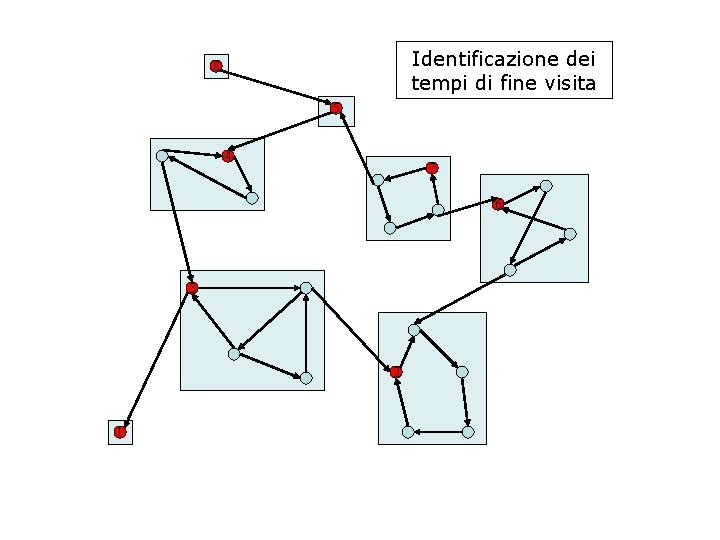
Identificazione dei tempi di fine visita 8 5 4 7 6 3 2 1

Transposizione del grafo 8 5 4 7 6 3 2 1

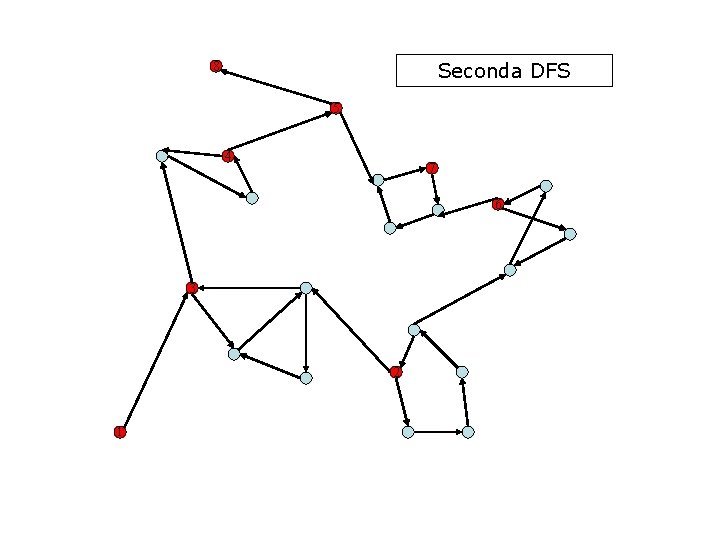
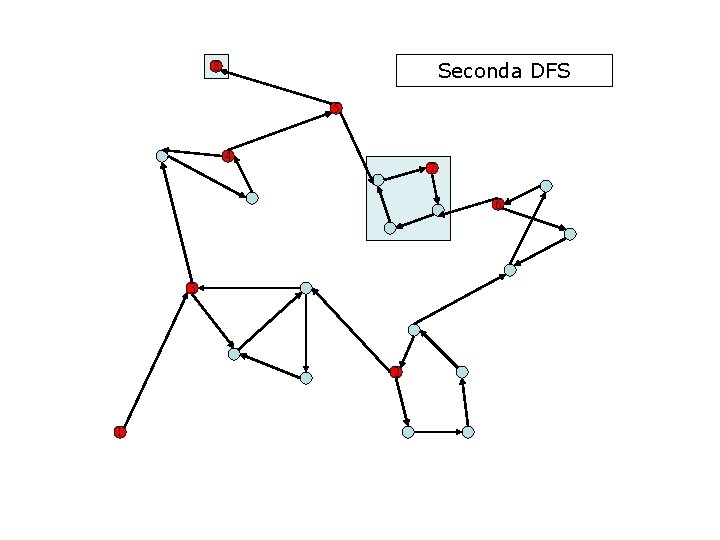
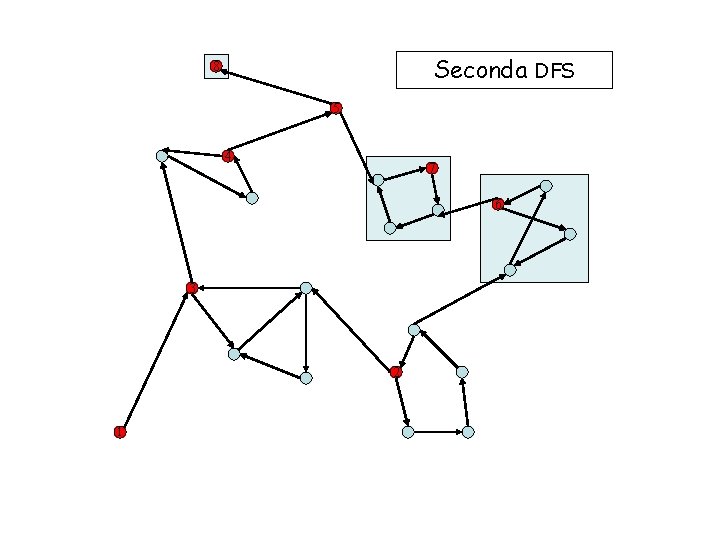
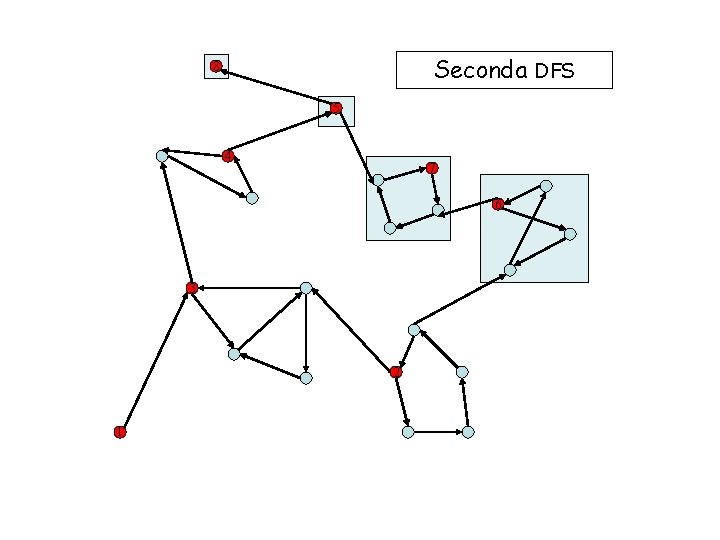
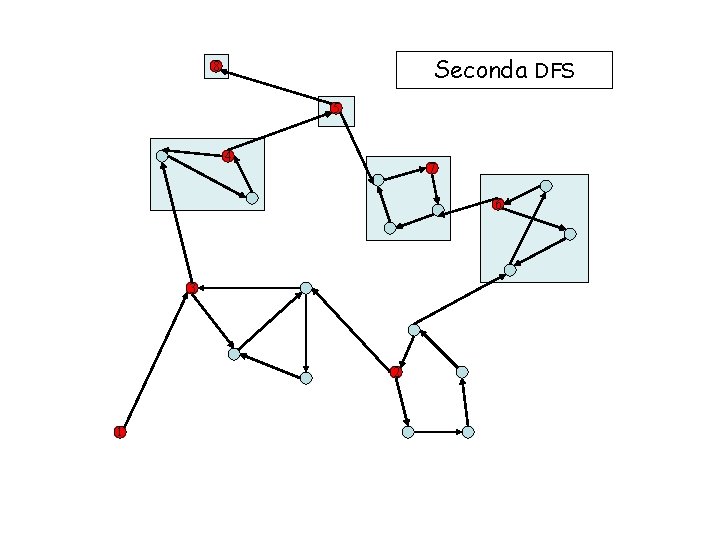
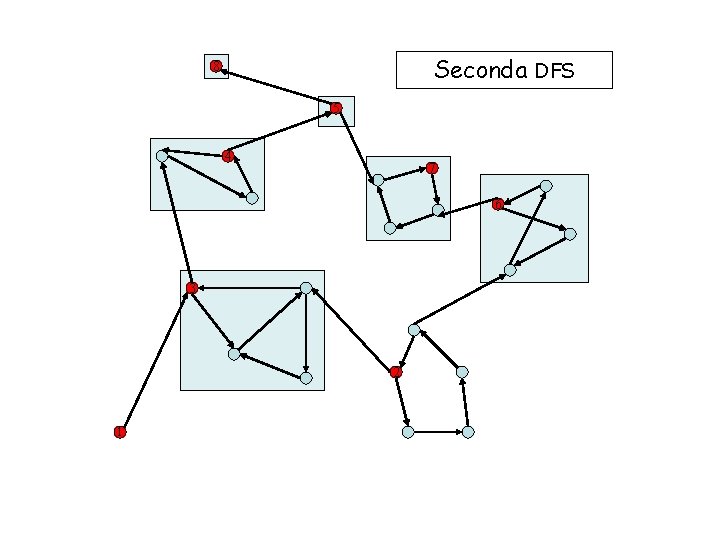
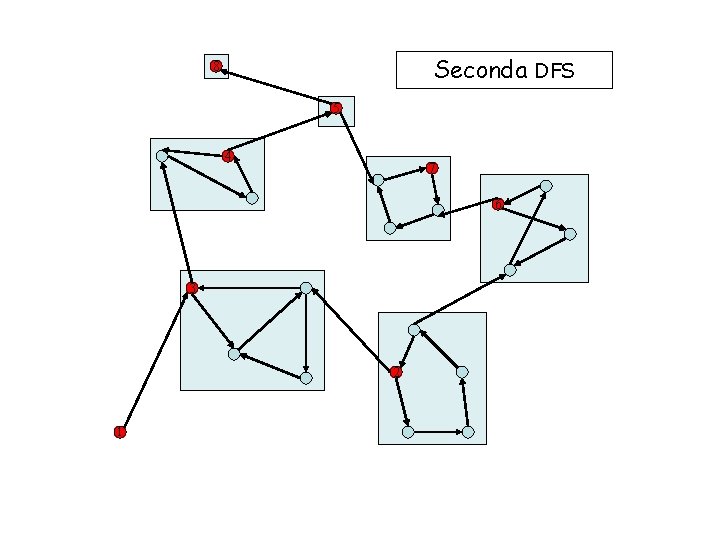
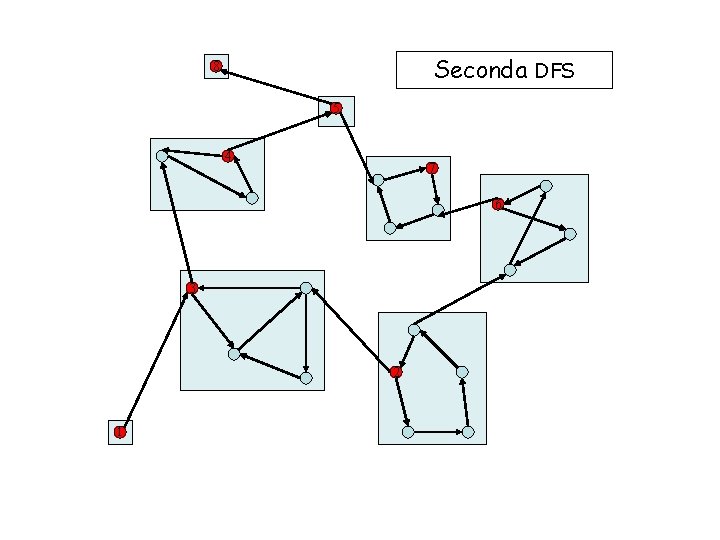
Seconda DFS 8 5 4 7 6 3 2 1

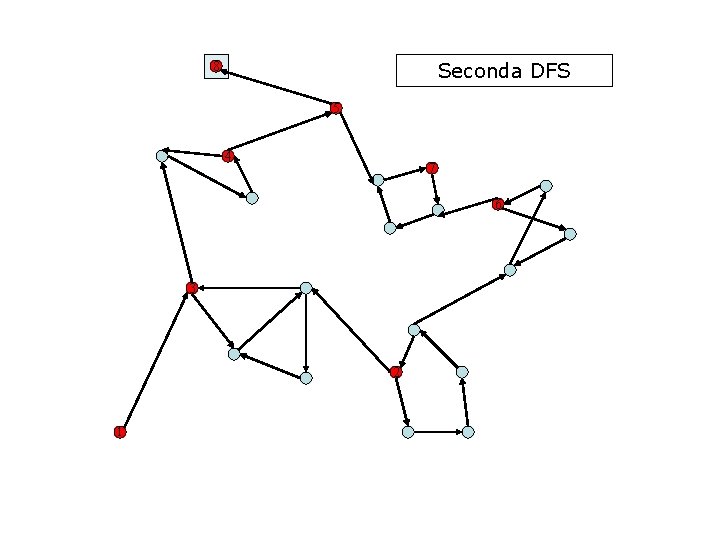
Seconda DFS 8 5 4 7 6 3 2 1

Seconda DFS 8 5 4 7 6 3 2 1

Seconda DFS 8 5 4 7 6 3 2 1

Seconda DFS 8 5 4 7 6 3 2 1

Seconda DFS 8 5 4 7 6 3 2 1

Seconda DFS 8 5 4 7 6 3 2 1

Seconda DFS 8 5 4 7 6 3 2 1

Seconda DFS 8 5 4 7 6 3 2 1