Complications for Categorical Syllogisms PHIL 121 Methods of

Complications for Categorical Syllogisms PHIL 121: Methods of Reasoning February 27, 2013 Instructor: Karin Howe Binghamton University

Overall Plan • First, I will present some problematic propositions and explain how we can deal with them (or not) • Second, we will discuss some problematic types of arguments and how we can deal with them (or not)

Problematic Propositions

• Issue 1: Statements that don't contain a quantifier – Example 1: Cats are mammals • This is clearly making a universal claim (it's talking about all cats, not just some of them) • Solution: Rewrite this statement as the following standard form categorical proposition "All cats are mammals. " • In general, when presented with a statement that seems categorical but does not contain a quantifier, we will assume it is making a universal claim unless we have good reasons to think otherwise. – Example 2: "Children are present" • This example is clearly an exception to the general rule I just stated. Clearly, this is not stating that all the children are present - it is merely saying that there are children here. • Solution: rewrite this statement as a standard form categorical proposition as follows: "Some children are people that are here. " (or something like that)

Issue 2: Compare the following two statements: – A bat is a mammal. • This is clearly making a universal statement -- it's talking about ALL bats, not about one particular bat. • Solution: "A bat is a mammal" can be translated into the standard form categorical proposition "All bats are mammals. " – A bat flew in the window. • However, this sentence is not making a universal claim. Rather, this is saying that there is some particular bat that flew into the window, and thus on the basis of this information we can make the claim "Some bats are things that fly into windows, " because we have at least one bat we can point to who did this. • Solution: "A bat flew into the window" can be translated into the standard form categorical proposition "Some bats are things that fly into windows. "

– Likewise for sentences with "an" or "the" -- sometimes these sentences make universal claims and sometimes they make claims about particular individuals, and thus should be treated as particular statements – We have to use context clues and what we know about the world in order to interpret them correctly – How about this statement? • "The cat is a fine animal commonly mistaken for a meatloaf. " – Does this statement make a universal claim, or is it making a particular claim? • Kind of ambiguous …. . • Sometimes we're just going to have to make a judgment call

• Issue 3: statements that are almost in standard form, but not quite • Example 1: Racehorses are all thoroughbreds. – Clearly, this is making a universal statement. How would we restate this as a standard form universal statement? – Careful! One temptation might be to take what follows "all" and make it the subject of the proposition, making the other term the predicate: "All thoroughbreds are racehorses. " (wrong!) – Solution: rewrite this statement in standard form as "All racehorses are thoroughbreds. "

• Example 2: All roly-poly fishheads are not good dancers. – Expressed symbolically: F = roly-poly fishheads, D = good dancers • All F are not D – Two possible solutions: • Although we are make a distinction between "not D" and "non-D", this distinction is in a certain sense an artificial and meaningless distinction. "not D" and "non-D" mean the same thing, so we could collapse the distinction in this case and rewrite this statement as "All roly-poly fishheads are non-gooddancers. " • Another possible solution is to just think about what this sentence is really saying. To say that all fishheads are not good dancers is simply to say that "No roly-poly fisheads are good dancers" (note that these solutions are equivalent via obversion)

• Issue 4: statements that are the negations of standard form categorical propositions – Not all birds can fly. • Expressed symbolically: B = birds, F = things that can fly – Not all B are F • Clearly, this is the negation of an A proposition. Based on the square of opposition, this is clearly equivalent to the corresponding O proposition. • Solution: rewrite this statement as a standard form categorical proposition as follows: "Some birds are not things that can fly. "

• There are no penguins in the Arctic. • This statement could naturally be read in two different but logically equivalent ways: – "It's false that some penguins are things that live in the Arctic" – "No penguins are things that live in the Arctic. " • Solution: always write statements of this form ("there are no X that are Y") as E propositions ("no X are Y"), since that way the statement will be in standard form

• Issue 5: statements with non-standard quantifiers such as "most, " "many, " "a few, " "all but a few, " "almost all, " "not quite all, " etc. • Solution: although it loses some of the meaning of these different quantifiers, we will translate all of these quantifiers as simply "Some" (captures the minimal meaning of these quantifiers) • Likewise, statements with the non-standard quantifiers "every, " "each, " or "any" are best understood as the standard quantifier "All. "

• • • Issue 6: statements involving "only" Example: Only mammals are marsupials Clearly, this is making some sort of universal claim. What universal claim is it making? Two options: 1. All mammals are marsupials. 2. All marsupials are mammals. Another way to think about it: Can be seen to be making the claim "If it's not a mammal, then it's not a marsupial" (because only mammals are marsupials). Well, this is the same as saying "All nonmammals are nonmarsupials, " which is the contrapositive of option 2 above. Solution: rewrite all statements of the form "Only X are Y" as "All Y are X"

• Issue 7: exceptive propositions (propositions that say things like "All except employees are eligible") • Clearly, this is making a universal claim, but what kind of universal claim? – In fact, is is asserting two universal claims. It is saying both that "all nonemployees are eligible" and that "no employees are eligible. " • Solution: rewrite these kinds of statements as the conjunction of the two underlying standard form propositions. Then, if we need to use these statements in an argument, we can just split them up into two premises, right? …. ? • Okay, that works, sort of, but there are issues with this, as we will come back to in the section about problematic arguments

• Issue 8: singular propositions (e. g. , "Karin is a kangaroo") • What kind of claim is this making? Is it making a universal claim, or is it making a particular claim? • Standard solution: – Symbolize the named individual as a unique unit class (as a set containing only that individual); e. g. K = {Karin} – Symbolize the predicate class as normal; e. g. G = kangaroos – Translate the statement as a universal statement; e. g. All K are G

• Copi says (in Ch 7) that it is "customary" to read these types of sentences this way "automatically" -- in other words, we simply interpret them this way naturally • Really? ? ? • Another problem with this solution: translating the statement "Karin is a kangaroo" as "All K are G" ignores the existence claim that the original statement is making. • Standard solution 2: Translate "Karin is a kangaroo" as the conjunction of the two statements "All K are G" and "Some K are G" • Both of these solutions are TERRIBLE. They are non-intuitive (especially the part about the unit class), and are in no way a match for the current standard logical treatment of these kinds of statements.

Summary: Problematic Propositions • Issue 1: statements that seem categorical in nature, but which don't contain an explicit quantifier. – Solution: we will generally treat these as making a universal claim, unless given good reason to think otherwise. • Issue 2: statements containing the words "a, " "an, " or "the" in place of a quantifier – Solution: use context clues to determine whether the statement is making a universal claim or a particular claim. Where this is ambiguous we will have to just make a judgment call (I will try not to give you statements where this is the case)

• Issue 3: statements that are almost in standard form, but not quite – Example 1: statements of the form "X are all Y" Solution: rewrite these statements as "All X are Y" – Example 2: statements of the form "All X are not Y" Solution: rewrite these statements as "All X are non. Y" or "No X are Y" • Issue 4: statements that are the negations of standard form categorical propositions – Solution: rewrite them as the corresponding contradictory proposition (e. g. , "Not all X are Y" would be rewritten as "Some X are not Y")

• Issue 5: statements with non-standard quantifiers such as "most, " "many, " "a few, " "all but a few, " "almost all, " "not quite all, " "every, " "each, " "any" etc. – Solution: translate non-standard quantifiers like "most, " "many, " "a few, " "all but a few, " "almost all, " "not quite all, " as "Some, " and translate non-standard quantifiers like "every, " "each" and "any" as "All" • Issue 6: statements involving "only" (e. g. "Only mammals are marsupials") – Solution: translate all statements of the form "Only X are Y" as "All Y are X"

• Issue 7: exceptive propositions (e. g. , "All except employees are eligible") – Solution: rewrite these kinds of statements as the conjunction of the two underlying standard form propositions. Then, if we need to use these statements in an argument, we can just split them up into two premises, right? …. ? • Issue 8: singular propositions (e. g. , "Karin is a kangaroo") – We cannot deal with these types of statements in syllogistic logic. Any attempts to do so are highly bizarre.

Problematic Arguments

Issue 1: Sorites • Pronounced so-ri-teas • In this context, a sorites is a categorical argument that contains three or more categorical propositions as premises • Like categorical syllogisms, categorical sorites can also be said to have a standard form

Standard Form Categorical Sorites 1. All statements are standard form categorical propositions 2. Each term appears exactly twice in the sorites. 3. Propositions are arranged in such a way that every proposition has one term in common with the proposition that follows it, except for the last proposition. 4. A line is drawn under the last proposition in the sorites. 5. The conclusion of the sorites appears under the line.

Example 1. All babies are illogical persons. 2. All illogical persons are despised persons. 3. No persons who can manage crocodiles are despised persons. __ Therefore no babies are persons who can manage crocodiles. In theory, we can use the Venn diagram technique to diagram this argument, with a little adjustment!

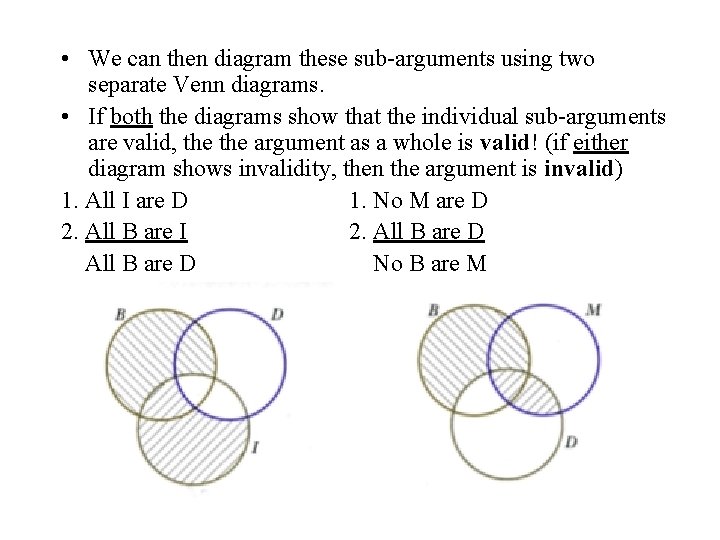
• Step 1: symbolize the argument 1. All babies are illogical persons. 2. All illogical persons are despised persons. 3. No persons who can manage crocodiles are despised persons. __ Therefore no babies are persons who can manage crocodiles. B = babies, I = illogical persons, M = people who can manage crocodiles, D = despised persons 1. All B are I 2. All I are D 3. No M are D Therefore No B are M

1. All B are I 2. All I are D 3. No M are D No B are M • Basically, what's going with a sorites is that there is a suppressed subconclusion that makes it all hang together - we need to bring out that subconclusion in order to split the argument into two standard form categorical syllogisms! 1. All I are D 1. No M are D 2. All B are I 2. All B are D No B are M

• We can then diagram these sub-arguments using two separate Venn diagrams. • If both the diagrams show that the individual sub-arguments are valid, the argument as a whole is valid! (if either diagram shows invalidity, then the argument is invalid) 1. All I are D 1. No M are D 2. All B are I 2. All B are D No B are M

Issue 2: Arguments with Inconsistent Premises § Explain why it is impossible for a standard form categorical syllogism to have inconsistent premises, making use of what you know about inconsistent premises and the relationships between standard form categorical propositions, as well as the definition of a standard form categorical syllogism.

Walking it through… • What is the definition of a set of inconsistent premises? – A set of premises is inconsistent if and only if it is impossible for them all to be true at the same time • What is the only way two categorical propositions can be inconsistent? (Hint: think about the Square of Opposition) – Answer: they have to be contradictory statements! (note: this is not universally true of a set of inconsistent statements, but is true in any set of two statements which are inconsistent)

• Okay, so pick any two pairs of contradictory statements and make them the premises of your argument: 1. All X are Y 2. Some X are not Y Therefore …. • • • What do you notice about this argument? It is not in standard form, because there is no middle term!! And that my children is why it is impossible to have a standard form categorical syllogism with inconsistent premises.

• But wait … didn't we say earlier that all arguments with inconsistent premises are valid? • Does that mean that there are some valid categorical syllogisms that we can't analyze using our Venn Diagram technique? ? • Well, maybe …. but maybe we can …. is there a way that we can use the Venn Diagram technique to show that an argument with inconsistent premises is valid?

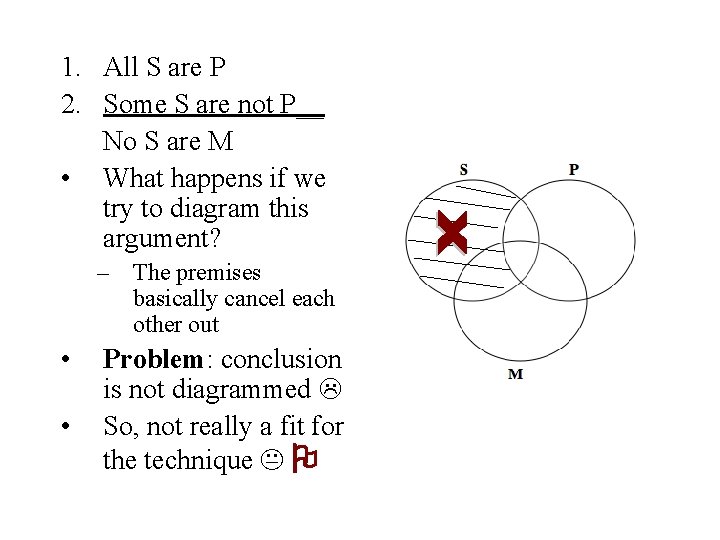
1. All S are P 2. Some S are not P__ No S are M • What happens if we try to diagram this argument? – The premises basically cancel each other out • • Problem: conclusion is not diagrammed So, not really a fit for the technique

Issue 3: arguments with exceptive premises • Consider the following statement: "All except students are wealthy. " • We could express this symbolically as the conjunction of these two statements: All non. S are W and No S are W (S = students, W = wealthy people) • Okay, what sort of conclusion could follow from this?

1. All non. S are W 2. No S are W____ Therefore …. ? § One option: § § W could be the middle term, in which case non. S would be the major term and S would be the minor term. However, that's not really right -- that's seeing three terms where there are only two

1. All non. S are W 2. No S are W____ Therefore …. ? § Easiest fix: § No S are W => No W are S (conversion) => All W are non. S (obversion) 1. All non. S are W 2. All W are non. S____ Therefore …. ? § Ooops! Not a standard form categorical syllogism!

• • 1. 2. 3. § Could this problem be fixed by adding another premise? In other words, suppose this was really a sorites, in disguise Example: All except students are wealthy. All wealthy people are happy. Therefore all nonstudents are happy. All non. S are W All W are non. S All W are H______ All non. S are H Yes, this would fix it -- all we would have to do is ignore the extraneous premise (P 2). (note however that it isn't really a sorites, though, because we still only have three terms) …. ?

Issue 4: Can the existential fallacy be fixed? • Consider the following argument: 1. All cats are cute things. 2. All cute things are soft things. Therefore some cats are soft things. The problem with this argument is that it depends on cats existing, which isn't given by the premises but which we know to in fact be the case.

• How about this as a solution? – Recall what Copi said in Chapter 3 -- it isn't really a problem that universals don't imply existence in the Boolean interpretation, because where existence is necessary for an argument, we can always add it in by writing the relevant universal statement both as a universal and a particular statement. 1. All cats are cute things. 2. Some cats are cute things. 3. All cute things are soft things. Therefore some cats are soft things. § Again, like in the previous example, it fixes the issue, but does so by ignoring one of the original premises (P 1) …. ?

1. All cats are cute things. 2. Some cats are cute things. 3. All cute things are soft things. Therefore some cats are soft things. § Again, like in the previous example, it fixes the issue, but does so by ignoring one of the original premises (P 1) § Again, this isn't really a problem (we can and should ignore irrelevant premises), but it's weird and non-standard.

Issue 5: Arguments containing singular statements 1. All kangaroos can fly. 2. Karin is a kangaroo. __ Karin can fly. § Since we can't analyze "Karin is a kangaroo" as a standard form categorical proposition, we are not able to analyze this argument using the Venn Diagram technique, even though it is clearly valid.

• Moral: while the Venn Diagramming technique can be expanded somewhat to deal with some kinds of non-standard categorical arguments (sorites) there are other arguments that are valid categorical arguments that we can't prove to be so using these tools. (likewise, we also can't prove certain argument invalid using these tools, either) • Doesn't make the Venn Diagramming technique a bad technique, just means it is limited. (which is why we need predicate logic, which we will not be able to cover in this class -- if you are interested in this you should take PHIL 122 in the summer or fall!)

Summary: Problematic Arguments • Issue 1: Sorites • Things you should know for the exam: – In this context, a sorites as a categorical argument that contains three or more categorical propositions – Like standard form categorical syllogisms, there is such a thing as a standard form sorites. – In theory, we can use our Venn Diagram technique to deal with these types of arguments – You should understand how to do this in theory, but you will not be asked to actually do it on the exam.

• Issue 2: arguments with inconsistent premises – The Venn Diagramming technique cannot be adapted to analyze these arguments • Issue 3: arguments with exceptive premises – These sometimes work, but sometimes don't -- it depends on the number of premises in the argument and the form of all of those premises …. ? • Issue 4: fixing the existential fallacy – If an argument commits the existential fallacy, but in this case the existence of the relevant class(es) is not in question, then we can simply add in the necessary particular statements. …. ? – Important caveat: Only works if we know the content of the argument -- can't be done if all we have is the form.

• Issue 5: arguments containing singular propositions – Since we cannot translate singular statements easily into standard form categorical propositions, this means that we can't deal with any arguments involving these types of statements using the Venn Diagram technique.