Complexity of Polynomial Systems David Pritchard Waterloo URA

Complexity of Polynomial Systems David Pritchard Waterloo URA Seminar May 16, 2007

Preliminaries • Polynomial equation: any expression using variables, constants, addition/subtraction, multiplication, whole powers, and one “=” • Polynomial system: multiple equations in a common set of variables. E. g. , x 3 ¡ 4 y 2 + 5 = 0; x = yz; 3(x + y) 100 = ab • Solution: a value for each variable, so after substituting, all equations are true. E. g. , x = ¡ 1; y = 1; z = ¡ 1; a = 0; b = 2007:

Motivation • Polynomial systems come up all over the place. Want general technique to answer: is there a solution? what is it? • Special case, e. g. : quadratic formula. • For this talk “general technique” means “computer program” • Want programs to be fast. Leads us to talk about computational complexity

Terminology • Important special case of polynomial is linear: no multiplication/powers of variables allowed. E. g. , x + 3 y = 5; (x + 1)y + 3 z = 5; x 2 ¡ x = 0 þ ý ý • In high school, learn how to solve 2 x 2 systems of linear equalities

Game Plan Real variables, linear polynomials Integer variables, linear polynomials Real* variables, Integer variables, arbitrary polynomials • Will discuss equalities and inequalities * or complex

Crash Course in Computational Complexity • A computer algorithm (program) is polynomial* time (P-time) if its running time on input I is at most C 1 si ze(I ) C 2 for some choice of constants C 1, C 2 • Math: “time” = steps on Turing machine. Us: “time” = ms of (say) Java program. Both notions are the same! * Distinct usage from polynomial system

Real Linear Equality Systems • Mentioned 2 var, 2 equation case • General strategy: Gaussian Elimination – solve for one variable x in terms of others – eliminate all occurrences of x – repeat: solve & eliminate another var, etc • Elimination ever gives “ 0=1”: no sol'n • Else back-substitute at end, get sol'n

Gaussian Elimination: Time • Say n vars, m eqns. Input size = n+m • # arithm’c operations to perform one round of substitution: 2 nm • Each round elims a var àn rounds • Total operations: 2 n 2 m < 2(input size)3 hence Gaussian elim’n is P-time • (We cheated - coefficient sizes, inter-mediate expression swell! Still P-time)

Real Linear Inequality Systems • Related to “linear programs: ” maximize f(x, y, …) subject to c 1(x, y, …) ≥ 0, c 2(x, y, …) ≥ 0, … where f, c 1, c 2, …, are linear functions • In fact optimizing is no harder than solving; use binary search like solve f(x, y, …) ≥ 10, f(x, y, …) ≤ 20, c 1(x, y, …) ≥ 0, c 2(x, y, …) ≥ 0, …

Linear Program Duality minimize $3 ¢beef + $4 ¢lamb+ $1 ¢oi l s. t. beef + lamb+ oi l ¸ 1 (1) beef + lamb ¸ 3=4 (2) 2 ¢beef + 4 ¢lamb ¸ 2 (3) • Notice (beef=1/2, lamb=1/4, oil=1/4) gives cost $2. 75. Is it optimal? • Yes! Add equations (1)+(2)+0. 5*(3): 3 ¢beef + 4 ¢lamb+ oi l ¸ 1 + 3=4 + 0: 5 ¢ 2 = 2: 75 • We can get a P-time solution, tricky

Scorecard Real variables, linear polynom’s P-time þ Integer variables, linear polynom’s [Khachiyan 1972] Real variables, any Integer variables, any polynomials

Integer Linear Systems • Application: similar to LP food example, but where can't break units (e. g. , scheduling employees) • Hard! Even in special case where all variables must be 0 or 1 • Naive algorithm: try all possibilities • n vars: need to try 2 n combinations, not P-time algorithm. Is there one?

What is NP-hardness? (NPh) • A problem (not algorithm) can be NPh • Doesn’t mean Non-Polynomial — actually “n” stands for nondeterministic • Yet, accepted evidence that no polynomial algorithm exists for the problem • Proof: reduce another NPh problem to it. Many, many problems are known to be NPh • Why evidence? Despite trying, no known P-time solution to any NPh problem • Suspicion: none exist! (i. e. , P != NP)

Integer Linear Programming • 0 -1 integer linear programming is NPh (Karp, 1972) • Removing “ 0 -1” only makes harder! • Effort still focused on practical solutions; for NPh problems, “real-life” instances may not be the hardest ones • E. g. , used to solve traveling salesman problem (NPh) on 100000 s of cities • One difficulty: no duality =(

Scorecard Real variables, linear polynom’s P-time þ [Khachiyan 1972] Integer variables, linear polynom’s NP-hard þ [Karp 1972] Real variables, any Integer variables, any polynomials

Real/Complex Polynomial Systems • Real vs complex leads to vastly different approaches to solve a polynomial system • Both are NP-hard! Proof… • Reduce to 0 -1 integer linear programming: – Suppose we can solve real polynomial systems – Then we could solve 0 -1 integer linear programs too: take linear constraints, add constraint x 2=x for each variable x – Increases problem size (#constraints, #vars) by only a little bit (a polynomial amount)

Systems in C: Gröbner Bases • Simplest Q: does a system have sol’n? • Recall: if we can manipulate system’s equations to get “ 0=1”, no solution • Basic idea: normalize system so that we can compute remainders (like mod) • Division by a set of polynomials is straightforward but can give multiple answers if set is not a Gröbner basis

Sketch of Complex Case 1. Normalize system to a Gröbner basis 2. Compute remainder of 1 in radical 3. If remainder is 0, there’s no solution; else remainder is 1, there’s a solution! • Depends on the fact that complex numbers are algebraically closed • Not as straightforward to numerically compute a solution

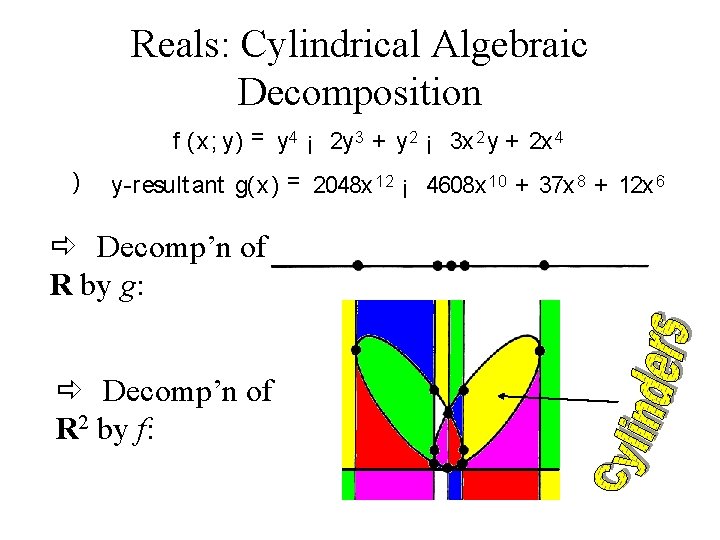
Reals: Cylindrical Algebraic Decomposition • Idea: polynomial system decomposes Euclidean space into several parts. • Compute parts recursively: use elimination (resultant) to reduce #vars e. g. from [Arnon, Collins, Mc. Callum 1984] y 4 ¡ 2 y 3 + y 2 ¡ 3 x 2 y + 2 x 4 = 0

Reals: Cylindrical Algebraic Decomposition f (x; y) = y 4 ¡ 2 y 3 + y 2 ¡ 3 x 2 y + 2 x 4 ) y-result ant g(x) = 2048 x 12 ¡ 4608 x 10 + 37 x 8 + 12 x 6 ð Decomp’n of R by g: ð Decomp’n of R 2 by f:

Scorecard Real variables, linear polynom’s P-time þ [Khachiyan 1972] Integer variables, linear polynom’s NP-hard þ [Karp 1972] Real variables, any Integer variables, any polynomials NP-hard þ [Buchberger 1965; Tarski 1930 s]

Integer Variables + Polynomials = Diophantine Equations • 1900, David Hilbert gave 23 problems to the international mathematics congress in Paris • Problem 10: “Find an algorithm to determine whether a given polynomial Diophantine equation with integer coefficients has an integer solution” • Exactly what we want to do!

(Different Formulations) • Whole number variables vs integer variables? Can write one using other: (whole number) – (whole number) = any integer [obvious] (integer)2 + (integer)2 = any whole number [Lagrange’s 4 -squares theorem] • Combine multiple eqn’s: {a=b, c=d} (a-b)2+(c-d)2=0

How to Solve Diophantine Eq’ns? • Can’t just try all possible solutions: if none found, can’t tell when to stop looking. • Any other technique works? • No! • Matiyasevich, 1970: No computer program exists that can determine solvability of Diophantine systems

Matiyasevich’s Theorem • Main contribution: proved anything a computer can do, a Diophantine sys’m can do 0 = wz + h + j - q • Random e. g. : 0 = (gk + 2 g + k + 1)(h + j) + h - z 0 = 16(k + 1) (k + 2)(n + 1) + 1 - f this system 0 = 2 n + p + q + z - e 0 = e (e + 2)(a + 1) + 1 - o has solution 0 = (a - 1)y + 1 – x if and only if 0 = 16 r y (a - 1) + 1 - u 0=n+l+v-y 0 = (a - 1)l + 1 - m k+2 is prime 3 3 2 2 2 4 2 2 2 2 0 = ai + k + 1 - l - i 0 = ((a + u 2(u 2 - a))2 - 1)(n + 4 dy)2 + 1 - (x + cu)2 0 = p + l(a - n - 1) + b(2 an + 2 a - n 2 - 2 n - 2) - m 0 = q + y(a - p - 1) + s(2 ap + 2 a - p 2 - 2 p - 2) - x 0 = z + pl(a - p) + t(2 ap - p 2 - 1) - pm

• Halting problem: Is there a computer program which takes other computer programs as input, and outputs whether or not they ever stop? • Answer: No! Proof: pretty! [not here] (Turing, 1936) • Hence: no program to solve Diophantine systems since (using simulation result) it would solve halting problem

Scorecard Real variables, linear polynom’s P-time þ [Khachiyan 1972] Integer variables, linear polynom’s NP-hard þ [Karp 1972] Real variables, any Integer variables, any polynomials NP-hard Uncomputable þ [Tarski 1930 s; Buchberger 1965] ý [Matiyasevich 1970]

Endgame • Many linear program solvers exist and simplex method doable by hand • Many integer LP solvers; can be much slower • Gröbner bases in Maple and… • CAD in Mathematica and… • Too bad for Diophantus and Hilbert =(