Complexity of Algorithms Whats on the menu Cost

Complexity of Algorithms

What’s on the menu? • Cost functions • O notation • Exercices Complexity of Algorithms

Why bother? If we give you a problem, you can program a solution. Making it work is not enough. ● When do we get the answer? Time complexity. ● How much space will it consume on the computer? Space complexity. It generally depends on the size of the problem. This size is often denoted by n. Your solution has to be efficient. Complexity of Algorithms

First example Compute the sum of elements in an array of size n. Spacecomplexity Time complexity int sum(int[] T){ int tmp = 0; for(int i = 0; i<T. size; i++) tmp = tmp + T[i]; return tmp; } Howmuch manyextra operations space does this functioninvolve? use? Repeated for each element in the 1. array. There are n elements. We have n additions. We also have n + 1 assignments. Complexity of Algorithms

Second example Find the largest element in an array of size n. int max(int[] T){ Space complexity Time complexity int tmp = T[0]; for(int i = 1; i < T. size; i++) if(T[i] > tmp) tmp = T[i]; return max; } Worst case. Average Best 1. case. Random data: loop each element has Themaximum overall will execute n– 1 Each element is than the The isgreater the first element. 50% chances be greater than the times, soone. n – to 1 comparisons. previous We never need this assignment. previous one. Total: n –many 1 comparisons +1 n. But – 1 how comparisons assignments? + n assignments. nassignment – 1 comparisons (temporary variable). ½(n – 1) + 1 assignments It depends on the data! Complexity of Algorithms

Hiii! That’s a mess! Yep. It is. We’ve seen two issues. Different cases in the data (worst, best, …) Different operations (assign, add, compare…) Complexity of Algorithms

Types of analysis: Formally We denote by In the set of all possible instances of size n. We denote by c(i) the cost of the algorithm on the instance i. ● Worst case: Walgorithm(n) = max{ c(i) | i in In} ● Best case: Balgorithm(n) = min{ c(i) | i in In} ● Average case: We denote p(i) the probability to obtain the instance i. If they all have the same probability, Complexity of Algorithms

Types of analysis: In practice Once you know which type of analysis you want, figure out the data. Example: find if an element is in an array of size n. bool is. In(int[] T, int e){ for(int i = 1; i < T. size; i++) if(T[i] == e) return true; return false; } Space complexity: 0. No assignment. Time complexity Worst Best case. The element we want is the last firstone in thethe in array. n 1 comparisons. comparison. Complexity of Algorithms

Types of operations Depending on the hardware you have, operations have different cost. • α for an addition • β for an assignment If you have n² additions and 20 n+100 assignments, then the cost is αn² + β(20 n+100) Complexity of Algorithms

Simplify! We don’t care about the differences in cost. Assume that’s all the same. αn² + β(20 n+100) → n² + 20 n + 100 When n gets large, it’s sufficient to identify the dominant term. • n = 2: 4 + 40 + 100 • n = 10: 100 + 200 + 100 • n = 100: 10 000 + 2 000 + 100 • n = 1000: 1 000 + 20 000 + 100 n² is the dominant term. We use the notation O and say that the algorithm is in O(n²). Complexity of Algorithms

O notation For a given cost function f(n), find the dominant term. Then you can say that f(n) belongs to one of the following classes: • O(1), constant dominant • O(log n), logarithmic • O(n), linear • O(n log n) • O(n²), quadratic • O(nc), polynomial Examples f(n) =f(n) 57 n² ==2+100 9 n 38 n (6 n)! +++5000 3 n 9 n² + 4923 +2 f(n) = (100 n²+log n)*(50+n ) linear constant 3) f(n) is in O(n). O(n²). O(n!). O(n • O(n!), factorial Complexity of Algorithms

O notation: a formal tool Saying that f(n) is in O(g(n)) means that there exists a constant c and a value n 0 thus that when n > n 0, then c. g(n) > f(n). • If f(n) is in O(g(n)) then c. f(n) is in O(g(n)). Example: 30 n² is in O(n²). Example f(n) = 39 n² + 30 is in O(n²). • If f 1(n) is in O(g(n)) and f 2(n) is in O(g(n)) then f 1(n) + f 2(n) is in O(g(n)). If we take 40 n² then there is a Example: 30 n² + n is in O(n²). value from which 40 n² is always greater than 39 n² + 30. • If f 1(n) is in O(g 1(n)) and f 2(n) is in O(g 2(n)) f 1(n) * f 2(n) The class ofthen complexity of the is in O(g 1(n) * g 2(n)). function is thus O(n²). Example: (30 n + log n + 3)*(7 n + 100) is in O(n*n) = O(n²) Complexity of Algorithms

Examples int sum(int[] blah(int[] T){T){ intint tmp = 0; res[] = new int[T. size]; for(int i =i = 0; 0; i<T. size; i++) for(int i<T. size; i++) Space complexity: O(1). Space complexity O(n). Time complexity: O(n). We do n times something that takes constant time. return tmp; /*** fundamental operations ***/ Time complexity O(n²). } return tmp; tmp = tmp + j<. T. size; T[i]; for(int j = 0; j++) } Complexity of Algorithms

Searching an element Here’s the algorithm whose complexity we just analyzed. . . bool is. In(int[] T, int e){ for(int i = 1; i < T. size; i++) if(T[i] == e) return true; return false; } What do you think? It’s SLOW! Complexity of Algorithms

What’s the idea? Currently, The algorithm we lookstops at each when stepit iffinds there theis element another you element askedtofor. check. Let’s just add it at. Ifthe not, end we to cannot ensurecontinue, we’ll stop. so we stop. Yes, but I found it Is it red? Is it after red? Is the it red? base. Is it red? stop base What about you stop looking and you just keep going until you hit the barrier? Complexity of Algorithms

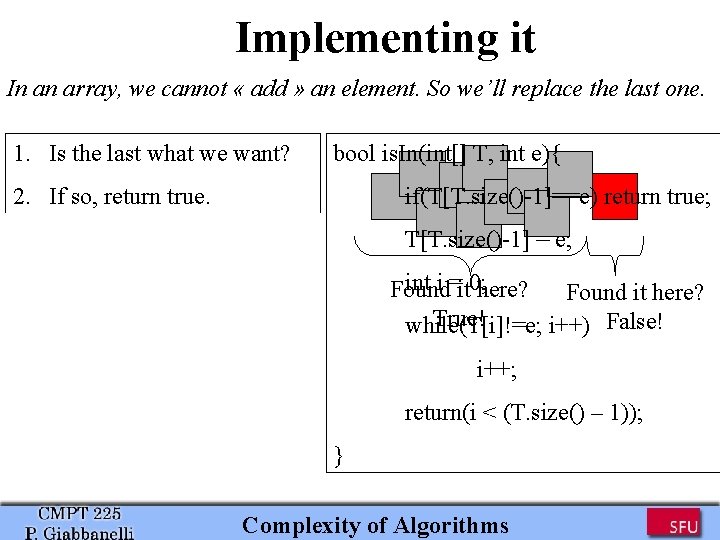
Implementing it In an array, we cannot « add » an element. So we’ll replace the last one. 1. Is the last what we want? bool is. In(int[] T, int e){ 2. If so, return true. if(T[T. size()-1]==e) return true; 3. Otherwise, replace the last one by what we want. T[T. size()-1] = e; int i =it 0; here? Found it here? True! while(T[i]!=e; i++) False! 4. Look until we find what we want. 5. Did we find it at the end? Then return false. Otherwise, return true. i++; return(i < (T. size() – 1)); } Complexity of Algorithms