Complexity metrics measure certain aspects of the software

Complexity metrics § measure certain aspects of the software (lines of code, # of if-statements, depth of nesting, …) § use these numbers as a criterion to assess a design, or to guide the design § interpretation: higher value higher complexity more effort required (= worse design) § two kinds: § intra-modular: inside one module § inter-modular: between modules 1

Sized-based complexity measures § counting lines of code (intra-modular) § differences in scale for different programming languages § Halstead’s metrics: counting operators and operands 2

Halstead’s metrics: § § n 1: number of unique operators n 2: number of unique operands N 1: total number of operators N 2: total number of operands 3

Example program public static void sort(int x []) { for (int i=0; i < x. length-1; i++) { for (int j=i+1; j < x. length; j++) { if (x[i] > x[j]) { operator, 1 occurrence int save=x[i]; x[i]=x[j]; x[j]=save } } operator, 2 occurrences 4

operator public sort() int [] {} for {; ; } if () = < … n 1 = 17 # of occurrences 1 1 4 7 4 2 1 5 2 … N 1 = 39 5

Example program public static void sort(int x []) { for (int i=0; i < x. length-1; i++) { for (int j=i+1; j < x. length; j++) { if (x[i] > x[j]) { int save=x[i]; x[i]=x[j]; x[j]=save } operand, 2 occurrences } 6

operand x length i j save 0 1 n 2 = 7 # of occurrences 9 2 7 6 2 1 2 N 2 = 29 7

Metrics: § § § § size of vocabulary: n = n 1 + n 2 program length: N = N 1 + N 2 volume: V = N log 2 n level of abstraction: L = V*/ V, V*=volume of fct prototype. For sort(x), V* = 2 log 2. For main(), L is high. approximation: L’ = (2/n 1)(n 2/N 2) programming effort: E = V/L estimated programming time: T ’ = E/18 estimate of N: N ’ = n 1 log 2 n 1 + n 2 log 2 n 2 for this example: N = 68, N ’ = 89, L =. 015, L’ =. 028 8

Remember… § Metrics are only estimates, give some idea on complexity § critique: § different definitions of “operand” and “operator” § explanations are not convincing (empirical, may not apply to other projects) § Source code must exist 9

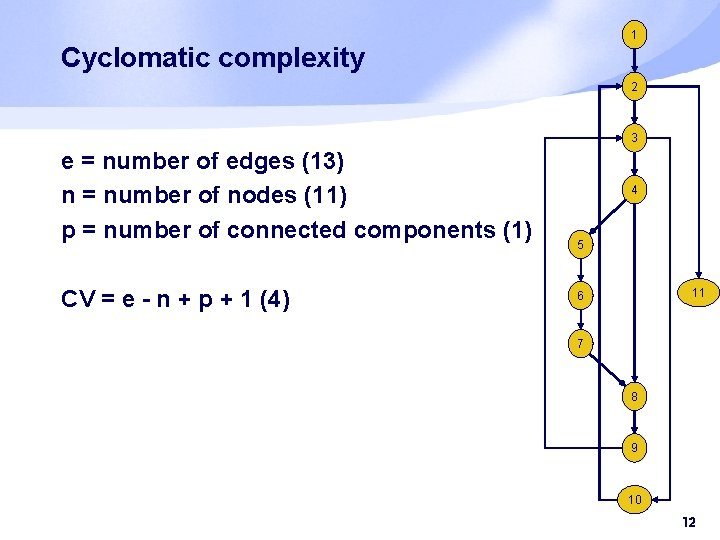
Other metrics (structure-based) § use § control structures § data structures § or both § example complexity measure based on data structures: average number of instructions between successive references to a variable § best known measure is based on the control structure: Mc. Cabe’s cyclomatic complexity 10

1 Example program 2 public static void sort(int x []) { for (int i=0; i < x. length-1; i++) { for (int j=i+1; j < x. length; j++) { if (x[i] > x[j]) { int save=x[i]; x[i]=x[j]; x[j]=save } } 3 4 5 11 6 7 8 9 10 11

1 Cyclomatic complexity 2 3 e = number of edges (13) n = number of nodes (11) p = number of connected components (1) CV = e - n + p + 1 (4) 4 5 11 6 7 8 9 10 12

Intra-modular complexity measures, summary § for small programs, the various measures correlate well with programming time § however, a simple length measure such as LOC does equally well § complexity measures are not very context sensitive § complexity measures take into account few aspects § it might help to look at the complexity density instead 13

System structure: inter-module complexity § measures dependencies between modules: draw graph: § modules =nodes § edges connecting modules may denote several relations, most often: A uses B (ex: procedure calls) 14

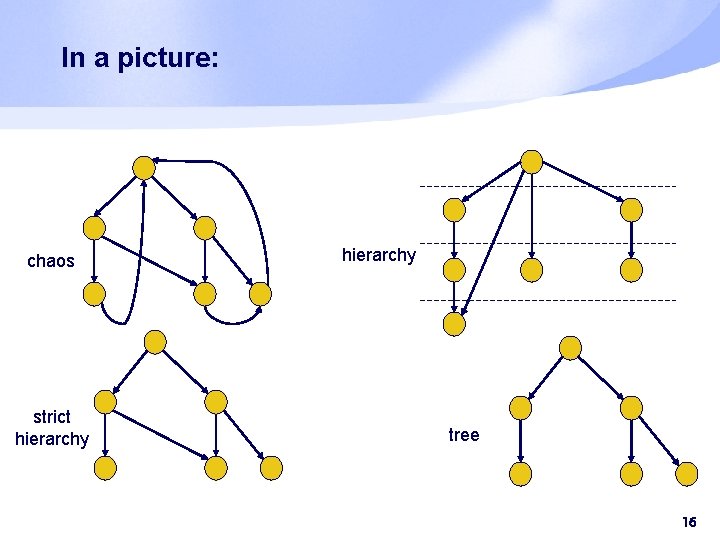
The uses relation § the call-graph § § chaos (general directed graph) hierarchy (acyclic graph) strict hierarchy (layers) tree 15

In a picture: chaos strict hierarchy tree 16

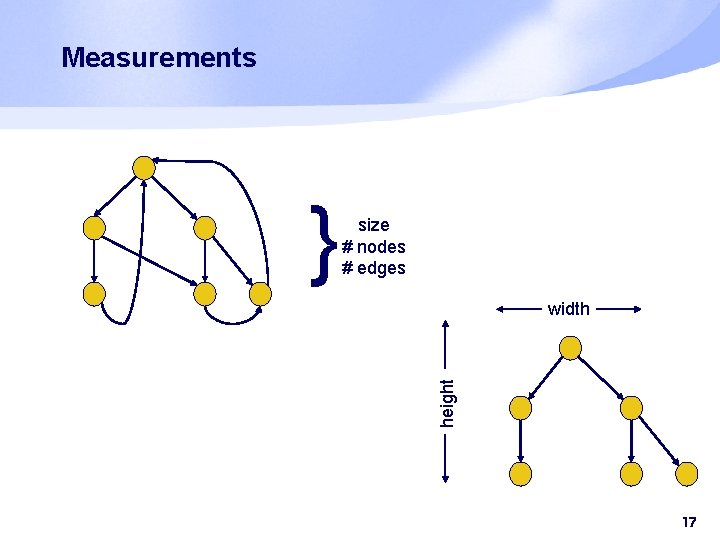
Measurements width height } size # nodes # edges 17

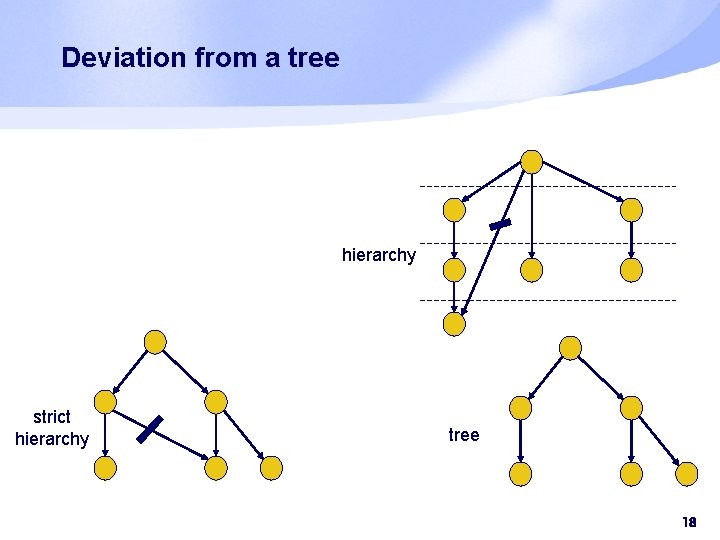
Deviation from a tree hierarchy strict hierarchy tree 18

Tree impurity metric § complete graph with n nodes has e = n(n-1)/2 edges § a tree with n nodes has e = (n-1) edges § tree impurity for a graph with n nodes and e edges: m(G) = 2(e-n+1)/(n-1)(n-2) (0 for tree, 1 for complete graph) 19

Any tree impurity metric: § m(G) = 0 if and only if G is a tree § m(G 1) > m(G 2) if G 1 = G 2 + an extra edge § if G 1 and G 2 have the same # of “extra” edges wrt their spanning tree, and G 1 has more nodes than G 2, then m(G 1) < m(G 2) § m(G) m(Kn) = 1, where G has n nodes, and Kn is the (undirected) complete graph with n nodes 20

Information flow metric § tree impurity metrics only consider the number of edges, not their “thickness” § Shepperd’s metric: § there is a local flow from A to B if: § A invokes B and passes it a parameter § B invokes A and A returns a value § there is a global flow from A to B if A updates some global structure and B reads that structure 21

Shepperd’s metric § fan-in(M) = # (local and global) flows whose sink is M § fan-out(M) = # (local and global) flows whose source is M § complexity(M) = (fan-in(M) * fan-out(M))2 22

Point to ponder: What does this program do? procedure X(A: array [1. . n] of int); var i, k, small: int; begin for i: = 1 to n do small: = A[i]; for k: = i to n-1 do if small <= A[k] then swap (A[k], A[k+1]) end end 23

Object-oriented metrics § § § WMC: Weighted Methods per Class DIT: Depth of Inheritance Tree NOC: Number Of Children CBO: Coupling Between Object Classes RFC: Response For a Class LCOM: Lack of COhesion of a Method 24

Weighted Methods per Class § measure for size of class § WMC = c(i), i = 1, …, n (number of methods) § c(i) = complexity of method i § mostly, c(i) = 1 25

Depth of Class in Inheritance Tree § DIT = distance of class to root of its inheritance tree § Good: forest of classes of medium height 26

Number Of Children § NOC: counts immediate descendants in inheritance tree § higher values NOC are considered bad: § possibly improper abstraction of the parent class § also suggests that class is to be used in a variety of settings 27

Coupling Between Object Classes § two classes are coupled if a method of one class uses a method or state variable of another class § CBO = count of all classes a given class is coupled with § high values: something is wrong § all couplings are counted alike; refinements are possible 28

Response For a Class § RFC = size of the “response set” of a class § response set = {set of methods: M} {set methods called by M 1: R 1} {R 2} … R 1 M 2 M 3 29

Lack of Cohesion of a Method § cohesion = glue that keeps the module (class) together, eg. all methods use the same set of state variables § if some methods use a subset of the state variables, and others use another subset, the class lacks cohesion § LCOM = number of disjoint sets of methods in a class § two methods in the same set share at least one state variable 30

OO metrics § WMC, CBO, RFC, LCOM most useful § Predict fault proneness during design § Strong relationship to maintenance effort § Many OO metrics correlate strongly with size 31