Complexity and Gdel Incomplete theorem B 90901144 Outline

Complexity and Gödel Incomplete theorem 電機三 B 90901144 劉峰豪

Outline n Introduction to the idea of “complexity” q q q n Complexity of some basic Operation Problems P and NP class Gödel Incomplete Theorem

Introduction n Big O, small O……. are too trivial Ln(r; c) for approximation of subexponential time P and NP class

Complexity of some Basic Operation n Given a, b q n n n size a = |a| = ln a +、-： *： /, %： O(max(size a, size b)) O(size a * size b) a=bq+r， O(size b * size q)

Ln n n is the input of a problem n Ln(r; c)= n Ln(0; c)：linear O((ln n)c) Ln(1; c)：exponential O( nc) n

Problems n n n Problem instance: a particular case of the task Search problem: it may have several correct answers Decision problem: answer yes or no

Some examples n Given N, and factor it q 6=2*3 n TSP n Does 91 have a factor between 2 and 63?

P and NP class n n n P NP NP-complete Reduction of problems Some applications in cryptography

P class n A decision problem p is in class P if there exists a constant c and an algorithm such that if an instance of p has input length <=n, then the algorithm answers the question in time O(nc)

Class NP n A decision problem p is in the class NP, if given any instance of p, a person with unlimited computing power can answer it “yes”, and another person can verify it in time P n P is in NP

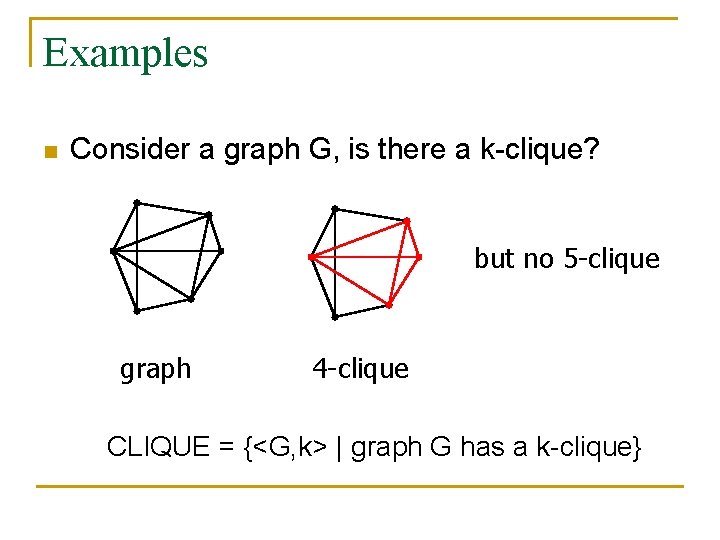
Examples n Consider a graph G, is there a k-clique? but no 5 -clique graph 4 -clique CLIQUE = {<G, k> | graph G has a k-clique}

Reducing one problem to another n Let p 1 and p 2 be 2 decision problems. We say that p 1 reduces to p 2 if there exists an algorithm that is polynomial time as a function of the input length of p 1 and that, given any instance P 1 of p 1, constructs an instance P 2 of p 2 such that the answer for P 1 is the same as the answer in P 2

Examples n P 1： input: a quadratic polynomial p(x) with integer coefficients Questions: does p(x) have two distinct roots? P 2： input：an integer N question: is N positive? P 1 reduces to P 2 p 1 < = p 2

NP completeness n A problem p is NP-complete q q n n if every other problem q in NP can be reduced to P in polynomial time p is in NP P = NP ? ? Relation between P and NPC? ?

Complexity and security of some cryptosystem n n n DES：linear or differential RSA：factorization ( quadratic sieve and number field sieve ) quadratic sieve： (Ln(1/2; c)) number field sieve：(Ln(1/3; c)) ECC：exponential time

RSA-576 Factored n n December 3, 2003 Number field sieve

Gödel Incomplete Theorem n n n Some Terms Theorem Effect

Some terms in Gödel Incomplete Theorem n n Consistent Undecidable Peano's Axioms Answer Hilbert's 2 nd Problem

Consistency n The absence of contradiction (i. e. , the ability to prove that a statement and its negative are both true) in an Axiomatic system is known as consistency. true A B false

undecidable n Not decidable as a result of being neither formally provable nor unprovable. q q A：”What B said is true. “ B：”What A said is false. “

Peano's Axioms q q q 1. Zero is a number. 2. If a is a number, the successor of a is a number. 3. zero is not the successor of a number. 4. Two numbers of which the successors are equal are themselves equal. 5. (induction axiom. ) If a set S of numbers contains zero and also the successor of every number in S, then every number is in S.

Gödel Incomplete Theorem n All consistent axiomatic formulations of number theory include undecidable propositions n Any formal system that is interesting enough to formulate its own consistency can prove its own consistency iff it is inconsistent.

Conclusions n n n All formal mathematical systems have only limited power. We will never be able to have a system that can prove all true statements about {0, 1, 2, …}, +, . Note that this result predates that of Turing and the solution of Hilbert’s polynomial problem.

Effect n Turing： general recursive functions n John Von Neumann n AI