Complex numbers What is There is no number

Complex numbers What is ? There is no number which squares to make -1, so there is no ‘real’ answer! Mathematicians have realised that by defining the imaginary number many previously unsolvable problems could be understood and explored. If , , what is: A number with both a real part and an imaginary one is called a complex number Eg Complex numbers are often referred to as z, whereas real numbers are often referred to as x The imaginary part of z, called Im z is 3 The real part of z, called Re z is 2 A complex number in the form is said to be in Cartesian form

Manipulation with complex numbers Techniques used with real numbers can still be applied with complex numbers: WB 1 z = 5 – 3 i, w = 2 + 2 i Express in the form a + bi, where a and b are real constants, (a) z 2 (b) a) Expand & simplify as usual, remembering that i 2 = 1 b) An equivalent complex number with a real denominator can be found by multiplying by the complex conjugate of the denominator If then its complex conjugate is

Modulus and argument The complex number can be represented on an Argand diagram by the coordinates Eg Eg Im Eg The modulus of z, Re Eg Eg Eg Remember the definition of arg z The principal argument is the angle from the positive real axis to in the range

WB 2 The complex numbers z 1 and z 2 are given by Find, showing your working, (a) in the form a + bi, where a and b are real, (b) the value of The modulus of (c) the value of is , giving your answer in radians to 2 decimal places. Im The principal argument is the angle from the positive real axis to in the range Re

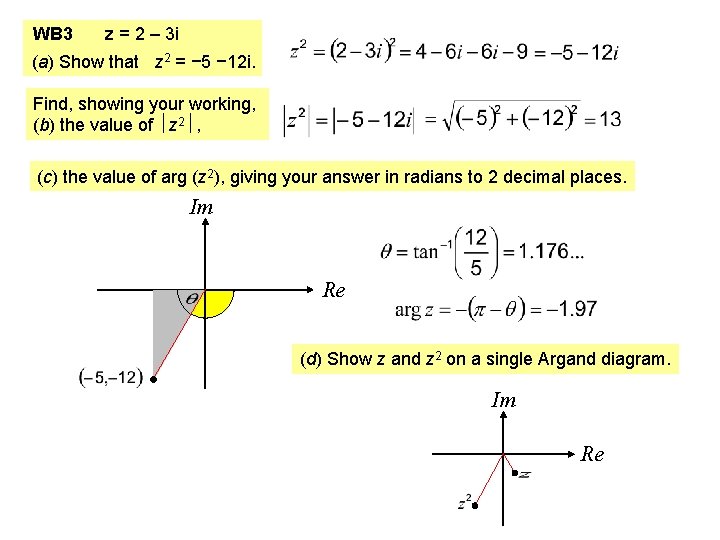
WB 3 z = 2 – 3 i (a) Show that z 2 = − 5 − 12 i. Find, showing your working, (b) the value of z 2 , (c) the value of arg (z 2), giving your answer in radians to 2 decimal places. Im Re (d) Show z and z 2 on a single Argand diagram. Im Re

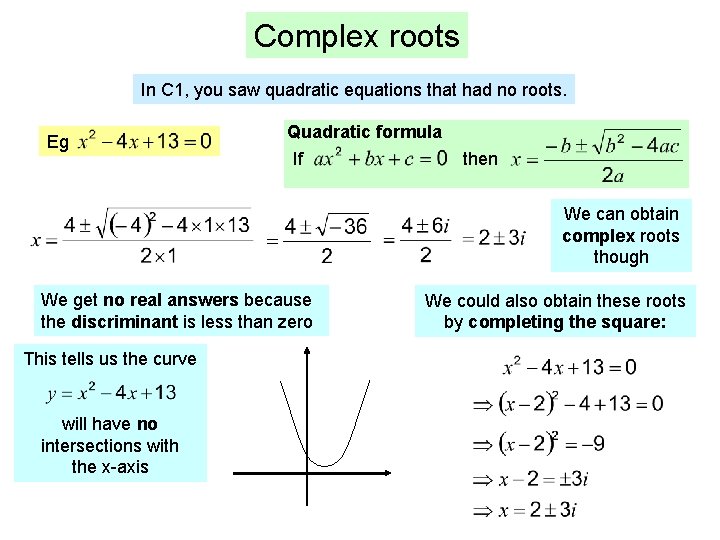
Complex roots In C 1, you saw quadratic equations that had no roots. Eg Quadratic formula If then We can obtain complex roots though We get no real answers because the discriminant is less than zero This tells us the curve will have no intersections with the x-axis We could also obtain these roots by completing the square:

WB 4 z 1 = − 2 + i (a) Find the modulus of z 1 (b) Find, in radians, the argument of z 1 , giving your answer to 2 decimal places. Im Re The solutions to the quadratic equation z 2 − 10 z + 28 = 0 are z 2 and z 3 (c) Find z 2 and z 3 , giving your answers in the form p i q, where p and q are integers. (d) Show, on an Argand diagram, the points representing your complex numbers Im Re

WB 6 Given that , where a and b are real constants, (a) find the value of a and the value of b. Comparing coefficients of x 2 Comparing coefficients of x 0 (b) Find the three roots of f(x) = 0. either (c) Find the sum of the three roots of f (x) = 0. So sum of the three roots is -1 or

Problem solving with roots In C 2 you met the Factor Theorem: Eg Given that x = 3 is a root of the equation (a) write down a factor of the equation, If a is a root of f(x) then is a factor , (b) Given that x = -2 is the other root, find the values of a and b is the other factor is the equation factorised expanding In FP 1 you apply this method to complex roots…

Problem solving with complex roots We have seen that complex roots come in pairs: Eg This leads to the logical conclusion that if a complex number is a root of an equation, then so is its conjugate We can use this fact to find real quadratic factors of equations: WB 5 Given that 2 – 4 i is a root of the equation z 2 + pz + q = 0, where p and q are real constants, (a) write down the other root of the equation, (b) find the value of p and the value of q. Factor theorem: If a is a root of f(x) then is a factor

WB 7 Given that 2 and 5 + 2 i are roots of the equation (a) write down the other complex root of the equation. (b) Find the value of c and the value of d. (c) Show the three roots of this equation on a single Argand diagram. Im Re

Problem solving by equating real & imaginary parts Eg Given that where a and b are real, find their values Equating real parts: Equating imaginary parts:

WB 8 Given that z = x + iy, find the value of x and the value of y such that z + 3 iz* = − 1 + 13 i where z* is the complex conjugate of z. then Equating real parts: Equating imaginary parts:

Eg Find the square roots of 3 – 4 i in the form a + ib, where a and b are real Equating real parts: Equating imaginary parts: as b real Square roots are -2 + i and 2 - i

Eg Find the roots of x 4 + 9 = 0 Equating real parts: Equating imaginary parts: Roots are

Modulus-argument form of a complex number Im If and then known as the modulus-argument form of a complex number Eg express in the form Re Eg express in the form From previously, and so

The modulus & argument of a product It can be shown that: Eg if and It can also be shown that: Eg if and Im Re This is easier than evaluating and then finding the modulus…

The modulus & argument of a quotient It can be shown that: Eg if and It can also be shown that: Eg if and From previously, This is much easier than evaluating and then finding the modulus…

WB 9 z = – 24 – 7 i (a) Show z on an Argand diagram. (b) Calculate arg z, giving your answer in radians to 2 decimal places. It is given that w = a + bi, Given also that given Re Modulus-argument form and (c) find the values of a and b (d) find the value of a ℝ, b ℝ. Im where and

Complex numbers Using: Manipulation with complex numbers Modulus and argument Also Im Re Complex roots w is a root of . Find the values of a and b Find the values of p and q Equating real & imaginary parts Equating real parts: Equating imaginary parts: