Complex Numbers Trigonometric Form Graph complex numbers Given

Complex Numbers: Trigonometric Form

· Graph complex numbers. · Given a complex number in standard form, find trigonometric, or polar, notation; and given a complex number in trigonometric form, find standard notation. · Use trigonometric notation to multiply and divide complex numbers. · Use De. Moivre’s theorem to raise a complex number to powers. · Find the nth roots of a complex number. Just as real numbers can be graphed on a line, complex numbers can be graphed on a plane. We graph a complex number a + bi in the same way that we graph an ordered pair of real numbers (a, b). However, in place of an xaxis, we have a real axis, and in place of a y-axis, we have an imaginary axis. Horizontal distances correspond to the real part of a number. Vertical distances correspond to the imaginary part.

WHAT ARE IMAGINARY AND COMPLEX NUMBERS? Do Now: Graph it Solve for x: x 2 + 1 = 0 ? What number when multiplied by itself gives us a negative one? No such real number parabola does not intersect x-axis NO REAL ROOTS

If then is not a real number, is a non-real or imaginary number. Definition: A pure imaginary number is any number that can be expressed in the form bi, where b is a real number such that b ≠ 0, and i is the imaginary unit. i

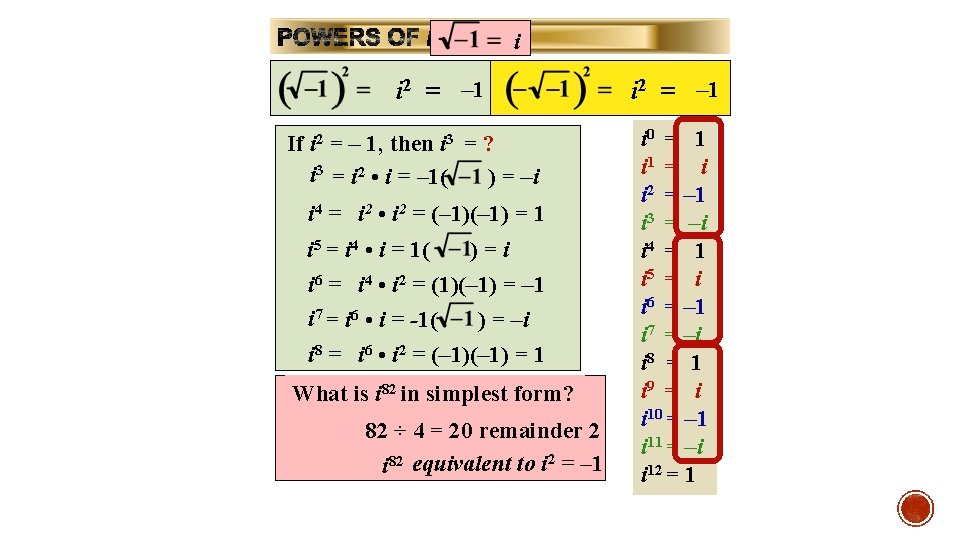
i i 2 = – 1 If i 2 = – 1, then i 3 = ? i 3 = i 2 • i = – 1( ) = –i i 4 = i 2 • i 2 = (– 1) = 1 i 5 = i 4 • i = 1( )=i i 6 = i 4 • i 2 = (1)(– 1) = – 1 i 7 = i 6 • i = -1( ) = –i i 8 = i 6 • i 2 = (– 1) = 1 What is i 82 in simplest form? 82 ÷ 4 = 20 remainder 2 i 82 equivalent to i 2 = – 1 i 0 = 1 i 1 = i i 2 = – 1 i 3 = –i i 4 = 1 i 5 = i i 6 = – 1 i 7 = –i i 8 = 1 i 9 = i i 10 = – 1 i 11 = –i i 12 = 1

Definition: A complex number is any number that can be expressed in the form a + bi, where a and b are real numbers and i is the imaginary unit. a + bi real numbers pure imaginary number Any number can be expressed as a complex number: 7 + 0 i = 7 a + bi 0 + 2 i = 2 i

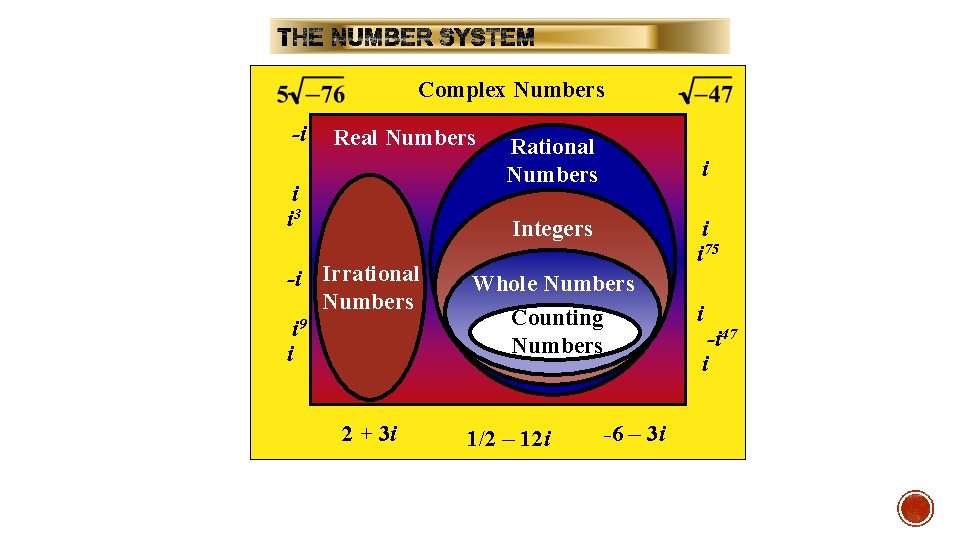
Complex Numbers -i Real Numbers i i 3 Rational Numbers i Integers -i Irrational Numbers i 9 i 2 + 3 i i i 75 Whole Numbers Counting Numbers 1/2 – 12 i -6 – 3 i i -i 47 i

Graph each of the following complex numbers. a) 3 + 2 i Solution: b) – 4 – 5 i c) – 3 i d) – 1 + 3 i e) 2

The absolute value of a complex number a + bi is

Find the absolute value of each of the following. Solution:

If we let be an angle in standard position whose terminal side passes through the point (a, b), then

Add/Subtract

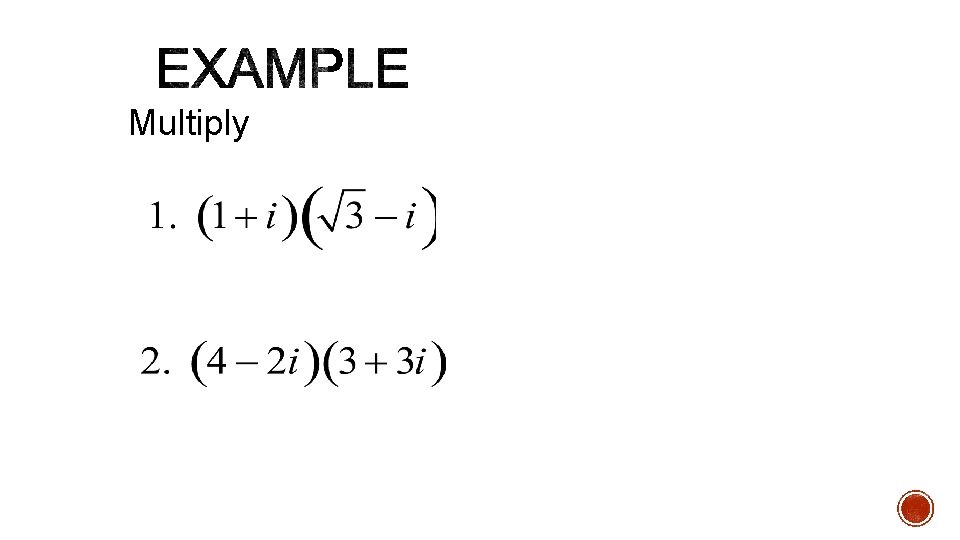
Multiply

Divide