Complex numbers Review Using Manipulation with complex numbers

Complex numbers Review Using: Manipulation with complex numbers Modulus and argument Also Im Re =0. 540 Complex roots w is a root of . Find the values of a and b Find the values of p and q Equating real & imaginary parts Equating real parts: Equating imaginary parts:

Complex numbers: modulus argument form KUS objectives BAT convert between the form a +bi and modulus argument form of a complex number Starter: see previous page

Modulus-argument form of a complex number y (Imaginary) z The modulus-argument form is an alternative way of writing a complex number, and it includes the modulus of the number as well as its argument. Hyp r θ rcosθ Adj By GCSE Trigonometry: S C O A H H rsinθ Opp x (Real)

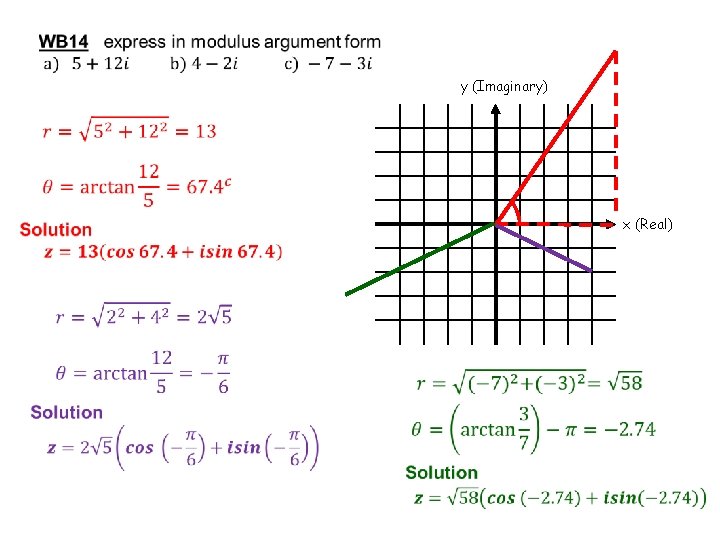
y (Imaginary) x (Real)

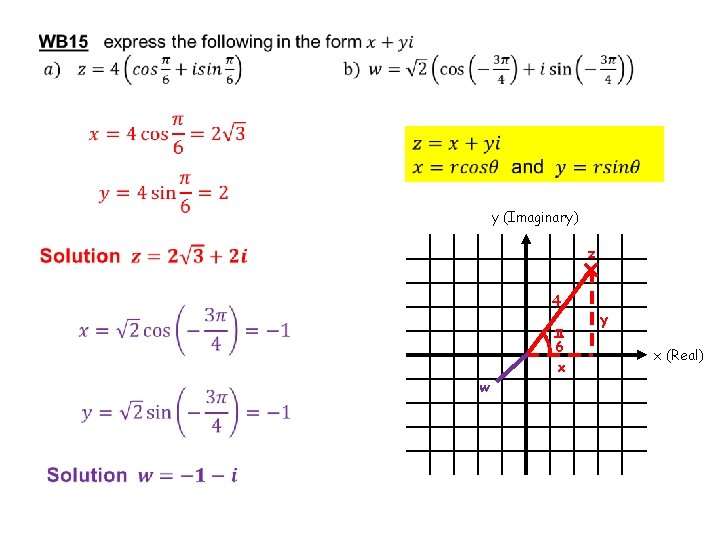
y (Imaginary) z 4 π 6 x w y x (Real)

y (Imaginary) Modulus for z 1 Argument for z 1 3 θ θ Modulus for z 2 Argument for z 2 Remember the angle you actually want! 3 z 2 1 √ 3 x (Real)

The modulus & argument of a product It can be shown that: It can also be shown that: The modulus & argument of a quotient It can be shown that: It can also be shown that: : Challenge – try constructing a proof of either result using modulus argument form of complex numbers

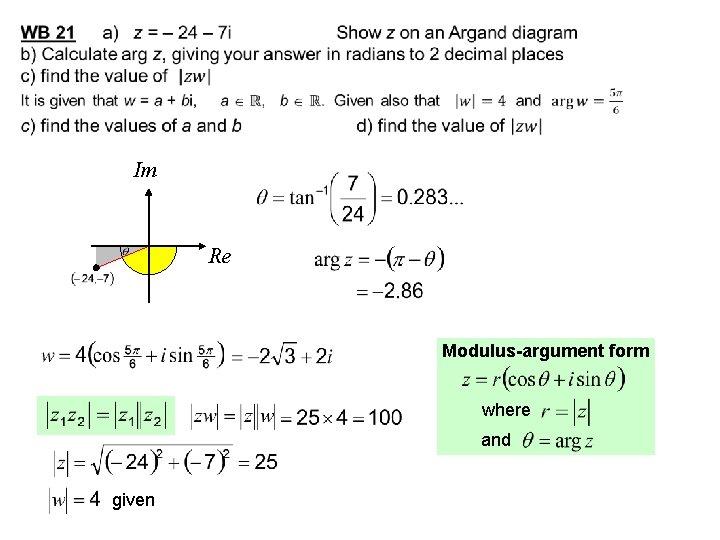
Im Re Modulus-argument form where and given

Summary Modulus-argument form of a complex number Im If and then known as the modulus-argument form of a complex number Re

KUS objectives BAT convert between the form a +bi and modulus argument form of a complex number self-assess One thing learned is – One thing to improve is –

END

Writing complex no in modulus argument form Imaginary axis x Real axis A complex number has both modulus and argument Then In modulus argument form