COMPLEX NUMBERS Reference Croft Davision Chapter 14 p

COMPLEX NUMBERS Reference: Croft & Davision, Chapter 14, p. 621 http: //www. math. utep. edu/sosmath 1. Introduction Extended the set of real numbers to find solutions of greater range of equations. Let j be a root of the equation Then and 1

Example 1. 1 Write down (a) , (b) , (c) Solution: (a) (b) (c) The number , imaginary number Complex numbers and V-01 are called 2

Example 1. 2 Simplify (a) , (b) Solution: (a) or (b) Complex numbers V-01 3

Example 1. 3 Solve Solution The solution are known as complex number. is a real part and Complex numbers (or ) is an imaginary part V-01 4

Complex Number • 16 th Century Italian Mathematician – Cardano • z = a + bj (Rectangular Form) – a: real number; real part of the complex number – b: real number; imaginary part of the complex number Im – bj: imaginary number a + bj b a Complex numbers V-01 Re 5

2. Algebra of Complex Numbers Addition and Subtraction of Complex Numbers If Complex numbers and then V-01 6

Example 2. 1 If and , find and Solution: Complex numbers V-01 7

Multiplication of complex numbers If Complex numbers and then V-01 8

Example 2. 2 Find if and . Solution: Complex numbers V-01 9

Example 2. 3 Find if and . Solution: Complex numbers V-01 10
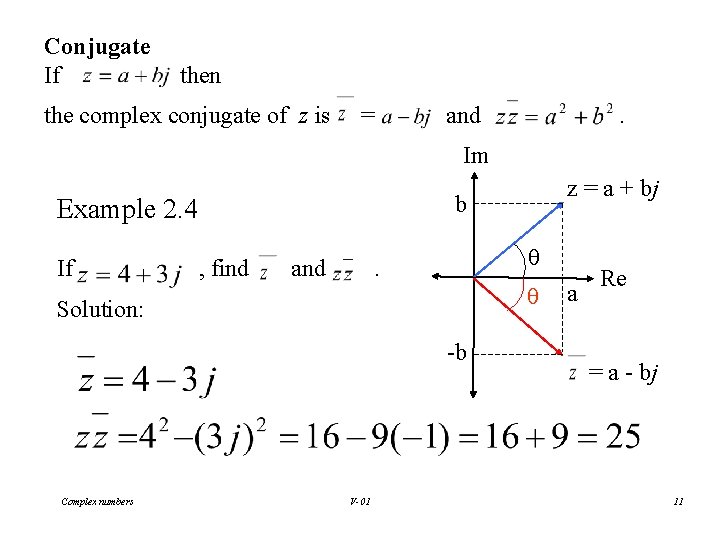
Conjugate If then the complex conjugate of z is = and . Im b Example 2. 4 If , find and θ . θ Solution: -b Complex numbers z = a + bj V-01 a Re = a - bj 11

Division of two complex numbers i. e. Complex numbers V-01 12

Example 2. 5 Simplify Solution: Complex numbers V-01 13

Example 2. 6 Simplify Solution: Complex numbers V-01 14

Example 2. 7 Simplify Solution: Complex numbers V-01 15

Equality of Complex Numbers If then and Example 2. 7 Find the values of x and y if . Solution: Complex numbers V-01 16

3. Argand Diagram, Modulus and Argument The representation of complex numbers by points in a plane is called an Argand diagram. Example 3. 1 Represent , and on an Argand diagram. Complex numbers V-01 17
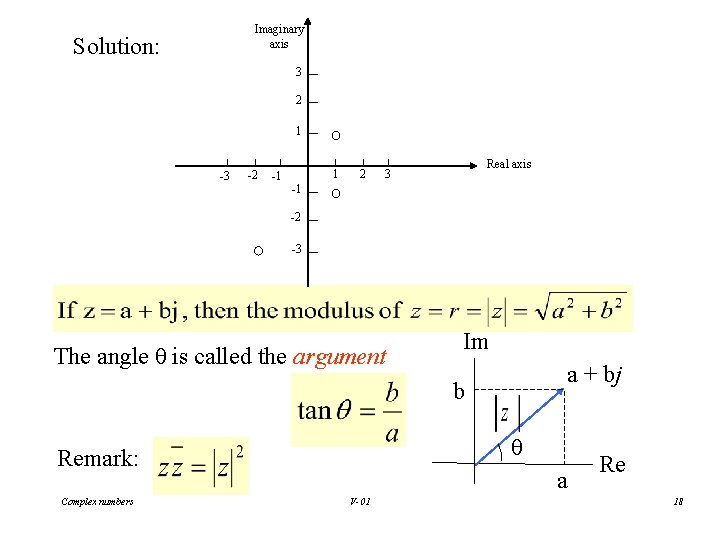
Imaginary axis Solution: 3 2 1 -3 -2 1 -1 2 Real axis 3 -1 -2 -3 The angle θ is called the argument Im a + bj b θ Remark: Complex numbers a V-01 Re 18

Example 3. 2 Find the modulus and argument of (a) (c) and (d). , (b) , Solution: Wrong ! Complex numbers V-01 19

Important Note !!! • Argument of a complex number The argument of a complex number is the angle between the positive x-axis and the line representing the complex number on an Argand diagram. It is denoted arg (z). Complex numbers V-01 20
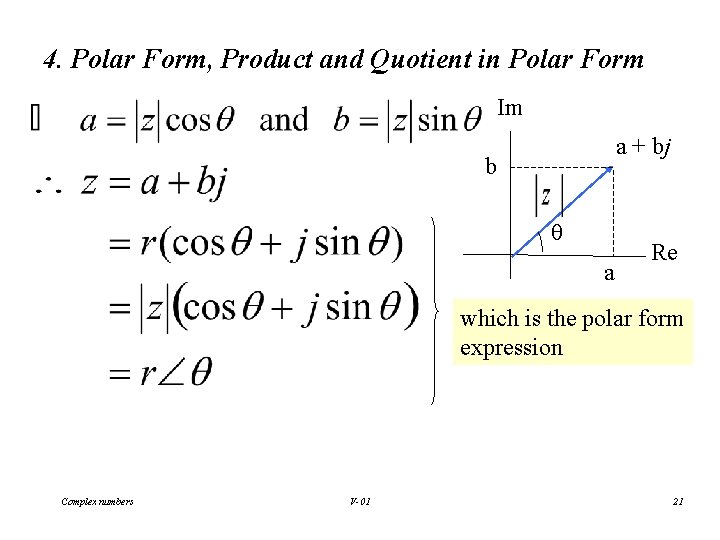
4. Polar Form, Product and Quotient in Polar Form Im a + bj b θ a Re which is the polar form expression Complex numbers V-01 21

Example 4. 1 Express the complex number in polar form. Solution: Wrong! 4 θ -3 Complex numbers V-01 α 22

Example 4. 2 Express in true polar form. Solution: A 3300 -300 C Complex numbers V-01 23

Let Complex numbers and V-01 . 24

Example 4. 3 If find and . Solution: Complex numbers V-01 25

Example 4. 4 Express the conjugate of true polar form. in Solution: Complex numbers V-01 26

5. Exponential Form To derive the exponential form we shall need to refer to the power series expansions of cos x, sin x … Complex numbers V-01 27

Euler’s Formula !!! Complex numbers V-01 28

Define and = = which is the exponential form expression and is in radian. Complex numbers V-01 29

Example 5. 1 Express the complex number exponential form. and its conjugate in Im Solution: a + bj b θ a Re which is the exponential form expression and is in radian. Complex numbers V-01 30

Example 5. 2 Find (a) and (b) . Solution: and which is the exponential form expression and is in radian. Complex numbers V-01 31

6. De Moivre’s Theorem Example 6. 1 Use De Moivre’s theorem to write in an alternative form. Solution Complex numbers V-01 32

Example 6. 2 If z = r(cos + j sin ), find z 4 and use De Movire’s theorem to write your result in an alternative form. Solution: z 4 = r 4 (cos + j sin )4 = r 4 (cos 4 + j sin 4 ) Complex numbers V-01 33

More concise form: If z = r then zn = rn n For example, z 4 = r 4 4 Example 6. 3 (a) If z = 2 /8 write down z 4. (b) Express your answer in both polar and Cartesian form. Solution (a) z 4 = 24 (4)( /8) = 16 /2 (b) i) z 4 = 16 (cos /2 + j sin /2) ii) a = 16 cos /2 = 0 b = 16 sin /2 = 16 Complex numbers V-01 34

Example 6. 4 If z = 3 (cos /12 + j sin /12) find z 3 in Cartesian form Solution z 3 = 33(cos(3)( /12) + j sin(3)( /12)) = 27(cos /4 + j sin /4) a = 27 cos /4 = 19. 09 b = 27 sin /4 = 19. 09 Complex numbers V-01 35

Example 6. 5 (a) Express z = 3 + 4 j in polar form. (b) Hence, find (3 + 4 j)10, leaving your answer in polar form. Solution Complex numbers V-01 36
- Slides: 36