COMPLEX NUMBERS Objectives Use the imaginary unit i

COMPLEX NUMBERS Objectives § Use the imaginary unit i to write complex numbers. § Add, subtract, and multiply complex numbers. § Use complex conjugates to write the quotient of two complex numbers in standard form. § Perform operations with square roots of negative numbers § Solve quadratic equations with complex imaginary solutions

Complex Numbers C Real Numbers R Integers Z Whole numbers W Natural Numbers N Rational Numbers Q R Irrational Numbers Q -bar Imaginary Numbers i

What is an imaginary number?

The Imaginary Unit i Previously, when we encountered square roots of negative numbers in solving equations, we would say “no real solution” or “not a real number”.

Complex Numbers & Imaginary Numbers

Adding and Subtracting Complex Numbers (5 − 11 i) + (7 + 4 i) Simplify and treat the i like a variable. = 5 − 11 i + 7 + 4 i = (5 + 7) + (− 11 i + 4 i) = 12 − 7 i Standard form

Adding and Subtracting Complex Numbers (− 5 + i) − (− 11 − 6 i) = − 5 + i + 11 + 6 i = − 5 + 11 + i + 6 i = 6 + 7 i
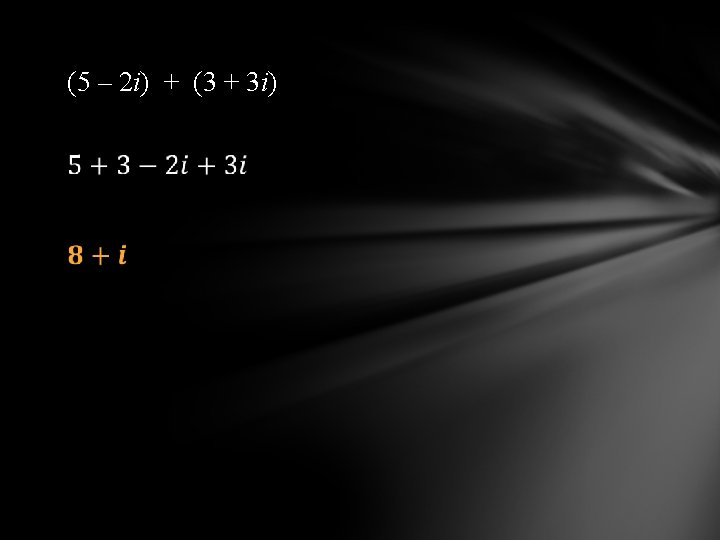


Multiplying Complex Numbers 4 i (3 − 5 i) Standard form

Multiplying Complex Numbers (7 − 3 i )( − 2 − 5 i) use FOIL Standard form

7 i (2 − 9 i) Standard form

(5 + 4 i)(6 − 7 i) Standard form

Complex Conjugates

Complex Conjugates

Complex Conjugates

Using Complex Conjugates to Divide Complex Numbers Divide and express the result in standard form: 7 + 4 i 2 − 5 i The complex conjugate of the denominator is 2 + 5 i. Multiply both the numerator and the denominator by the complex conjugate.

Using Complex Conjugates to Divide Complex Numbers

Divide and express the result in standard form: 5 + 4 i 4−i

Roots of Negative Numbers

The complex-number system is used to find zeros of functions that are not real numbers. When looking at a graph of a function, if the graph does not cross the x-axis, it has no real-number zeros.

- Slides: 22