Complex numbers Loci in the Argand diagram KUS

Complex numbers: Loci in the Argand diagram KUS objectives BAT Use complex numbers to represent a region of points on an Argand diagram Starter:

Reminder: 6 types of transformations of graphs
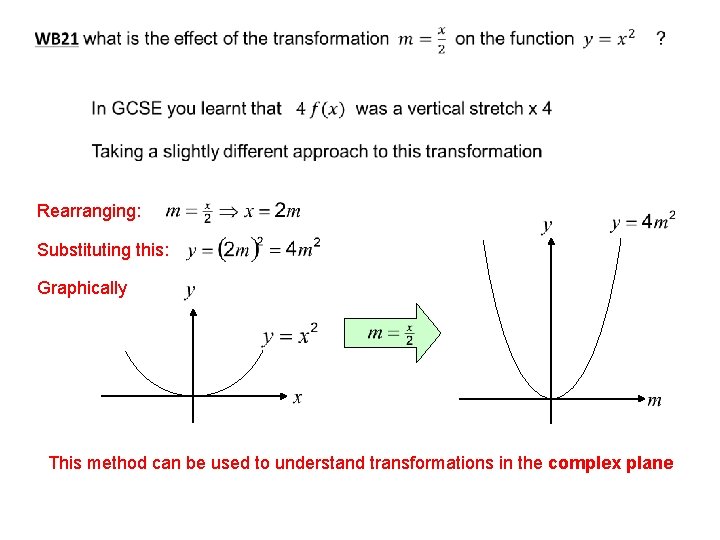
Rearranging: Substituting this: Graphically This method can be used to understand transformations in the complex plane
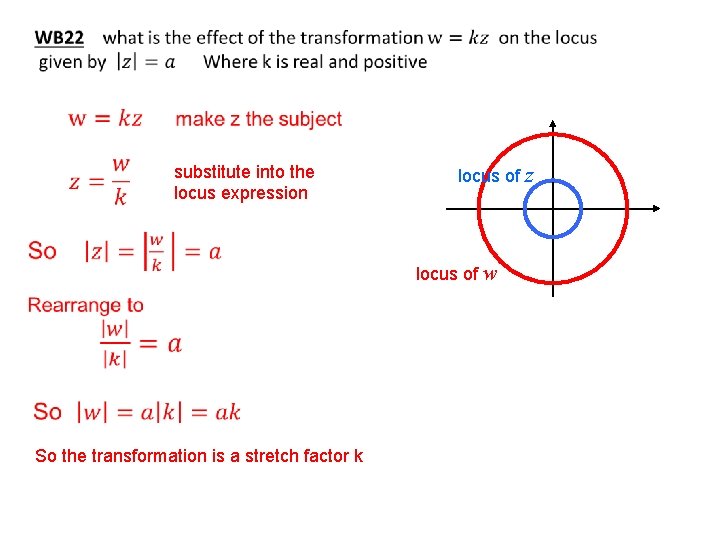
substitute into the locus expression locus of z locus of w So the transformation is a stretch factor k
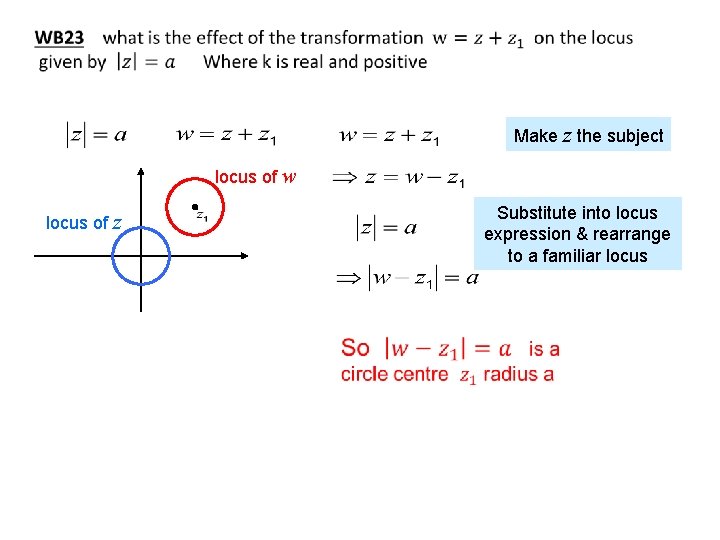
Make z the subject locus of w locus of z Substitute into locus expression & rearrange to a familiar locus
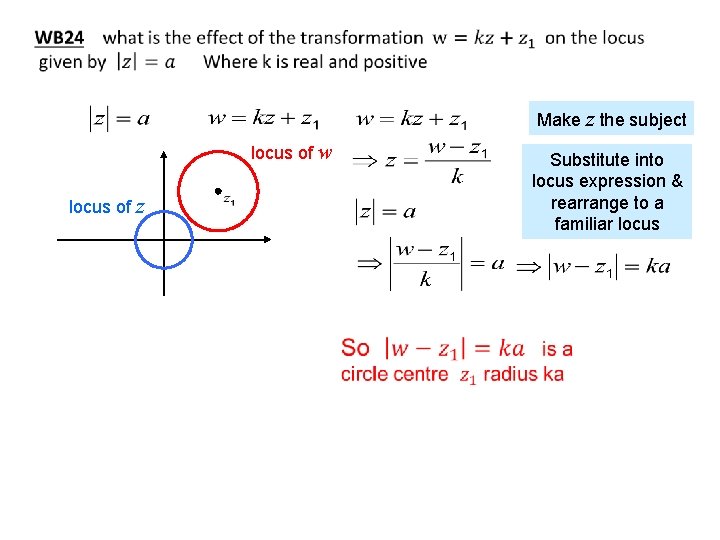
Make z the subject locus of w locus of z Substitute into locus expression & rearrange to a familiar locus

Summary so far Other transformations are less obvious to spot, but can be interpreted using the same method as before • Make z the subject • Substitute into locus expression & rearrange to a familiar locus
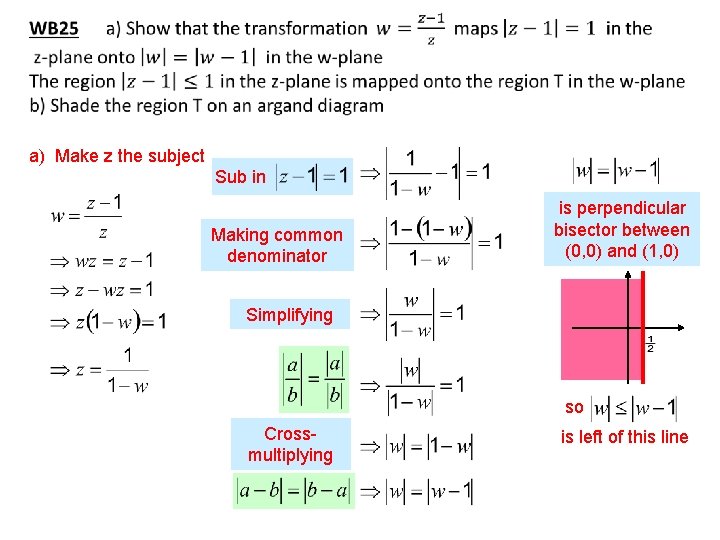
a) Make z the subject Sub in Making common denominator is perpendicular bisector between (0, 0) and (1, 0) Simplifying so Crossmultiplying is left of this line


As z can be anywhere on the real axis and so its locus is z = x + 0 i, we need to manipulate our expression into this locus of w form, starting by using the complex conjugate in order to separate real and imaginary parts. We can then equate them with the known expression for z = x + 0 i

locus of w Use

C L

P is the locus of z such that , found previously Make z the subject Sub in ‘Part of a line’ suggests keep in arg( ) form is a half-line starting from w at an angle of 90 o to (1, 0)

WB 30 June 11 Q 5 – pure evil Most questions ask you to transform z onto w, this question does the opposite Hence you want to consider an expression for w in terms of z = x + iy R on x-axis

The perfect formula? When But if This gives and in the exponential form this gives Im Re This single formula brings together key concepts in mathematics – integers, negative numbers, pi, exponentials, real and complex numbers! Complex numbers have many applications in Mathematics, science and engineering. What started as an ‘imaginary’ concept actually turns out to have many real applications such as fluid dynamics, electrical engineering, control systems in mechanical systems, quantum mechanics, relativity and differential equations in areas as far reaching as economics and biology.

KUS objectives BAT Use complex numbers to represent a region of points on an Argand diagram self-assess One thing learned is – One thing to improve is –

END
- Slides: 18