Complex numbers Loci in the Argand diagram KUS

Complex numbers: Loci in the Argand diagram KUS objectives BAT Use complex numbers to represent a locus of points on an Argand diagram Starter:

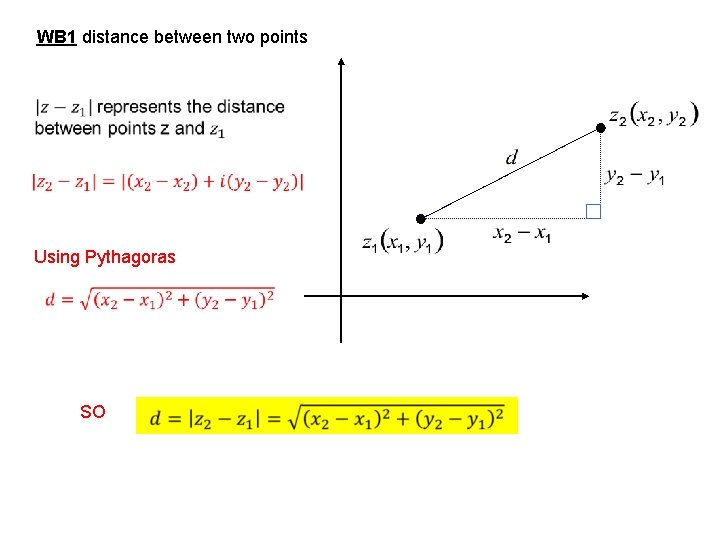
WB 1 distance between two points Using Pythagoras SO

WB 2 Loci of a circle with complex numbers In GCSE, you learnt that the circle is the set of points equidistant from a point locus of z describes the circle with centre z 1 and radius r This can be easily proved Square both sides This is the Cartesian equation of a circle with centre (x 1, y 1) and radius r

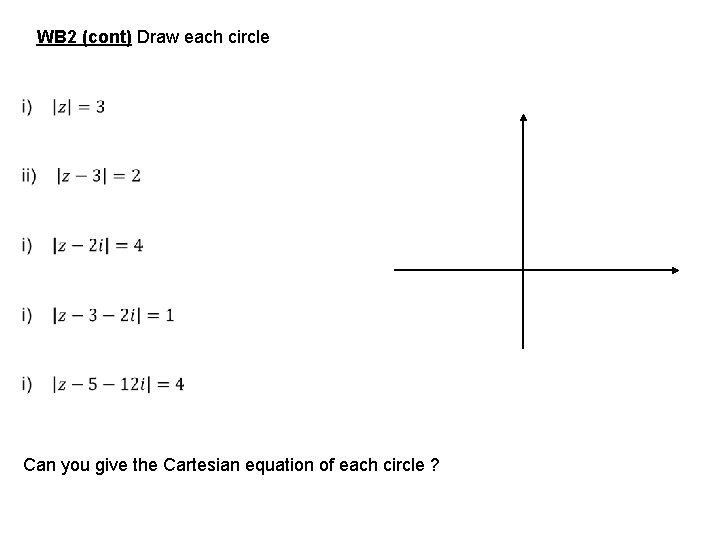
WB 2 (cont) Draw each circle Can you give the Cartesian equation of each circle ?

Im 5 4 The values of z are z = 3 i and z = -3 i Re

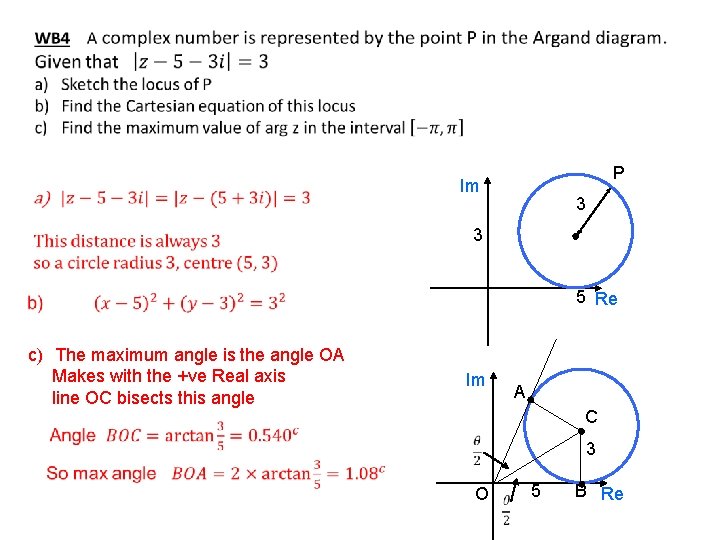
P Im 3 3 5 Re c) The maximum angle is the angle OA Makes with the +ve Real axis line OC bisects this angle Im A C 3 O 5 B Re

Im 3 X O 3 Y C(12, 5) Re

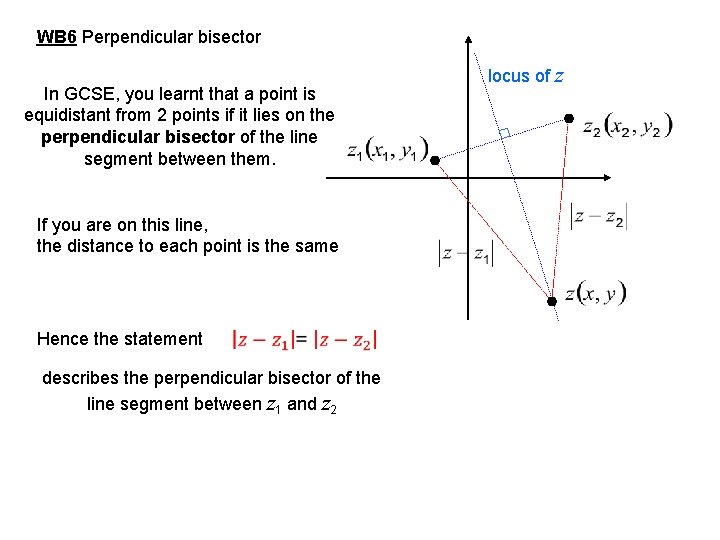
WB 6 Perpendicular bisector In GCSE, you learnt that a point is equidistant from 2 points if it lies on the perpendicular bisector of the line segment between them. If you are on this line, the distance to each point is the same Hence the statement describes the perpendicular bisector of the line segment between z 1 and z 2 locus of z

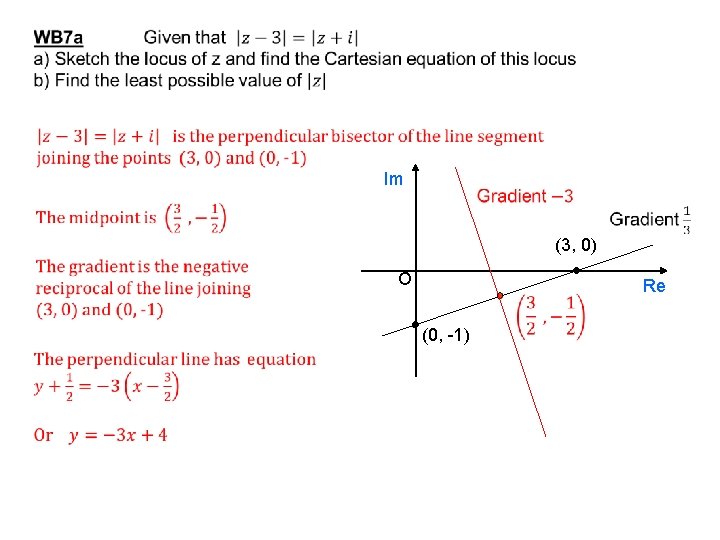
Im (3, 0) O Re (0, -1)

Im (3, 0) O Re (0, -1)

Im (3, 0) Square the Real and imaginary parts O Re (0, -1) Often squaring both sides is the quickest way to a solution

Collecting real and imaginary parts Squaring locus of z Circle centre (-10, 12) radius 10

Collecting real and imaginary parts Squaring locus of z

KUS objectives BAT Use complex numbers to represent a locus of points on an Argand diagram self-assess One thing learned is – One thing to improve is –

END