Complex numbers Loci in the Argand diagram KUS

Complex numbers: Loci in the Argand diagram KUS objectives BAT Use complex numbers to represent a locus of points on an Argand diagram Starter: see previous page

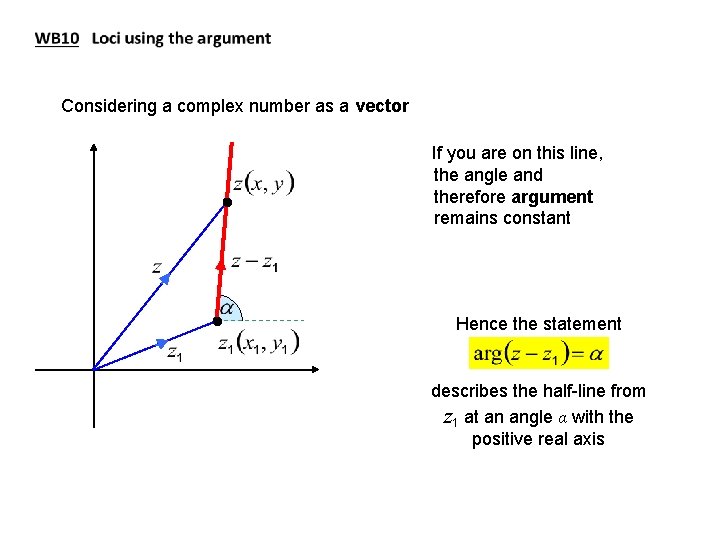
Considering a complex number as a vector If you are on this line, the angle and therefore argument remains constant Hence the statement describes the half-line from z 1 at an angle α with the positive real axis

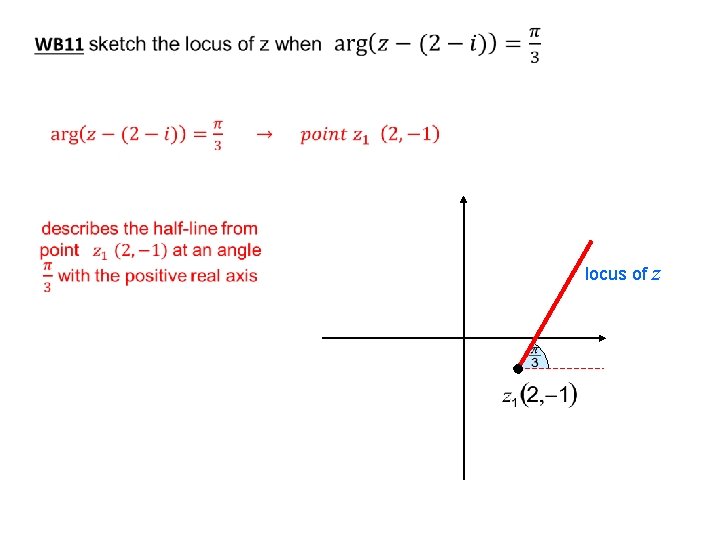
locus of z

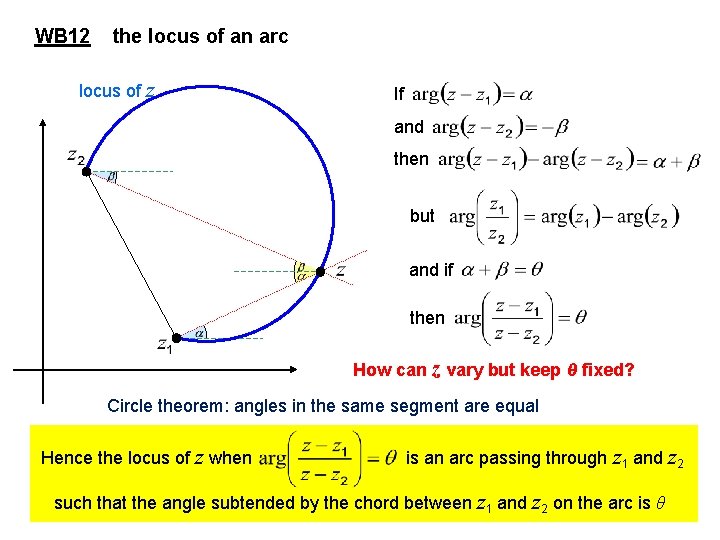
WB 12 the locus of an arc locus of z If and then but and if then How can z vary but keep θ fixed? Circle theorem: angles in the same segment are equal Hence the locus of z when is an arc passing through z 1 and z 2 such that the angle subtended by the chord between z 1 and z 2 on the arc is θ

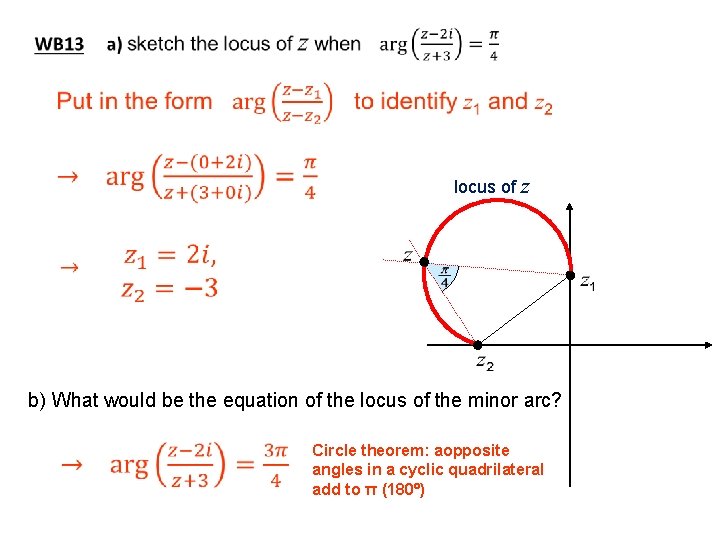
locus of z b) What would be the equation of the locus of the minor arc? Circle theorem: aopposite angles in a cyclic quadrilateral add to π (180 )

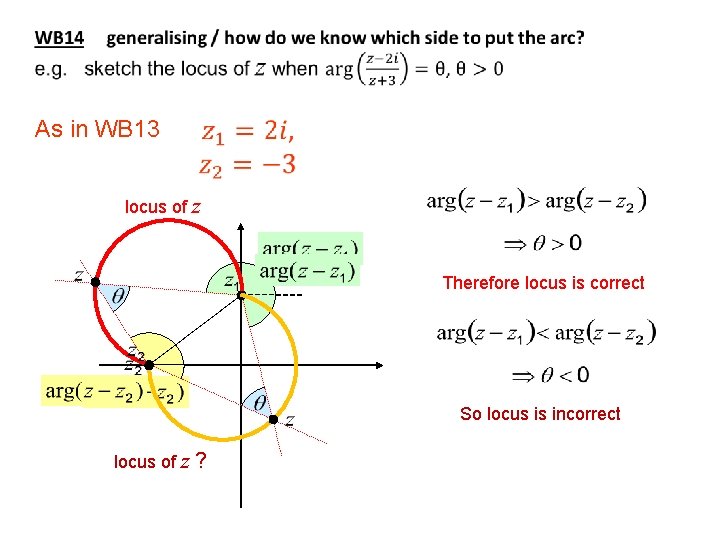
As in WB 13 locus of z Therefore locus is correct So locus is incorrect locus of z ?

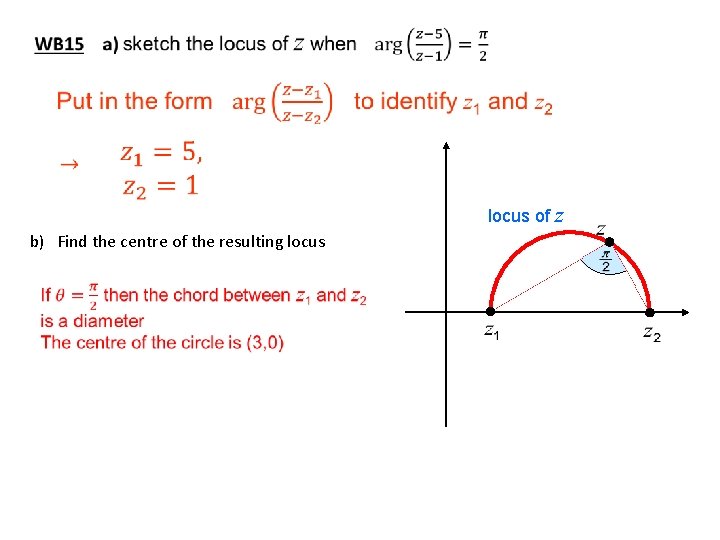
locus of z b) Find the centre of the resulting locus

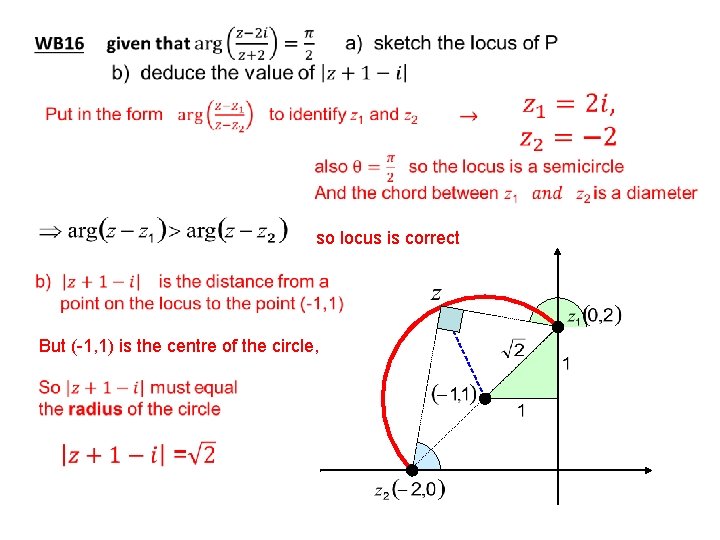
so locus is correct But (-1, 1) is the centre of the circle,

The half-line from (1, 0) passes through the centre of the circle As the angle is , the triangle is isosceles Using Pythagoras,

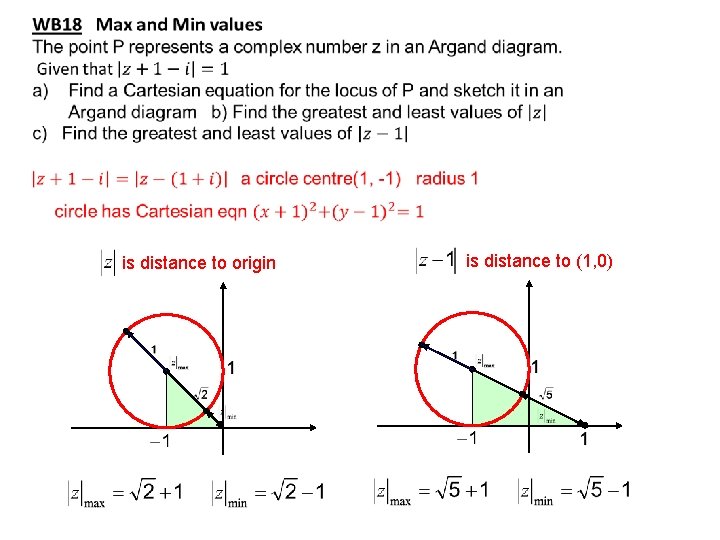
is distance to origin is distance to (1, 0)

KUS objectives BAT Use complex numbers to represent a locus of points on an Argand diagram self-assess One thing learned is – One thing to improve is –

END