Complex numbers KUS objectives BAT Know how to

Complex numbers KUS objectives BAT Know how to represent and use Argand diagrams Starter: Evaluate the following:

WB 1 Argand diagrams Real numbers can be represented on a number line Complex numbers are represented on an Argand diagram Imaginary axis 4 + 3 i Real axis

WB 1 (cont) Argand diagrams Imaginary axis Real axis Represent these complex numbers on an Argand diagram: What do you notice about the position of a complex number and its conjugate?

You can use Pythagoras’ Theorem to find the magnitude of the distances y (Imaginary) z 1 5 i √ 29 z 3 1 -5 5 √ 17 2 3 4 4 5 5 -5 i z 2 x (Real)

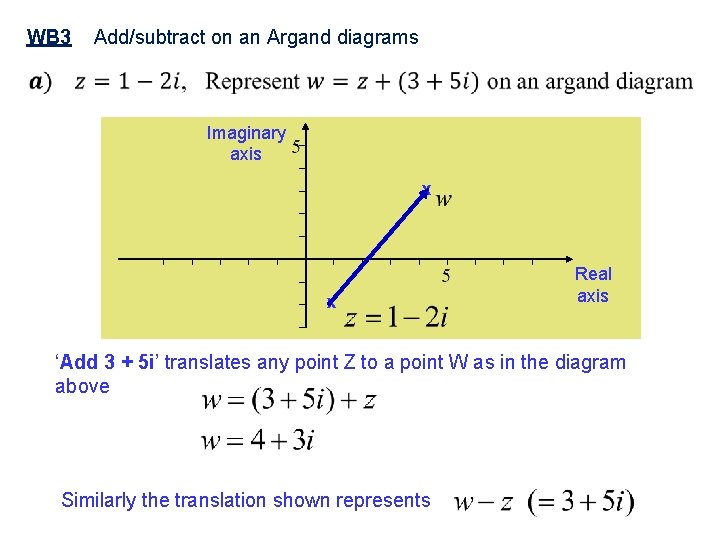
WB 3 Add/subtract on an Argand diagrams Imaginary axis x x Real axis ‘Add 3 + 5 i’ translates any point Z to a point W as in the diagram above Similarly the translation shown represents

WB 3 Add/subtract on an Argand diagrams Imaginary axis Real axis

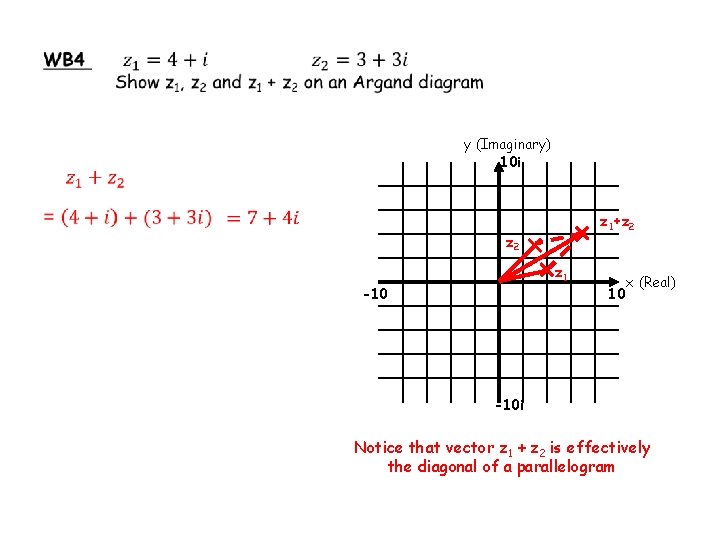
y (Imaginary) 10 i z 1+z 2 z 1 -10 10 x (Real) -10 i Notice that vector z 1 + z 2 is effectively the diagonal of a parallelogram

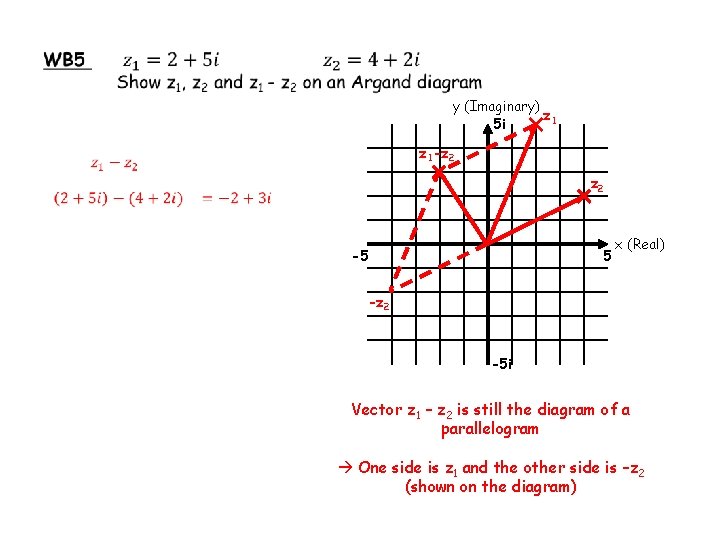
y (Imaginary) z 1 5 i z 1 -z 2 -5 5 x (Real) -z 2 -5 i Vector z 1 – z 2 is still the diagram of a parallelogram One side is z 1 and the other side is –z 2 (shown on the diagram)

WB 6 Argand diagram – multiplication by a real number Imaginary axis x x Real axis This is similar to multiplication of real numbers – the relation between points Z and W is that W is 3 times as far from O as Z

WB 7 Argand diagram – multiplication by conjugate Imaginary axis x x Real axis

KUS objectives BAT Know how to represent and use Argand diagrams self-assess One thing learned is – One thing to improve is –

END