Complex Numbers and i is the imaginary unit

Complex Numbers and i is the imaginary unit Numbers in the form a + bi are called complex numbers § a is the real part § b is the imaginary part

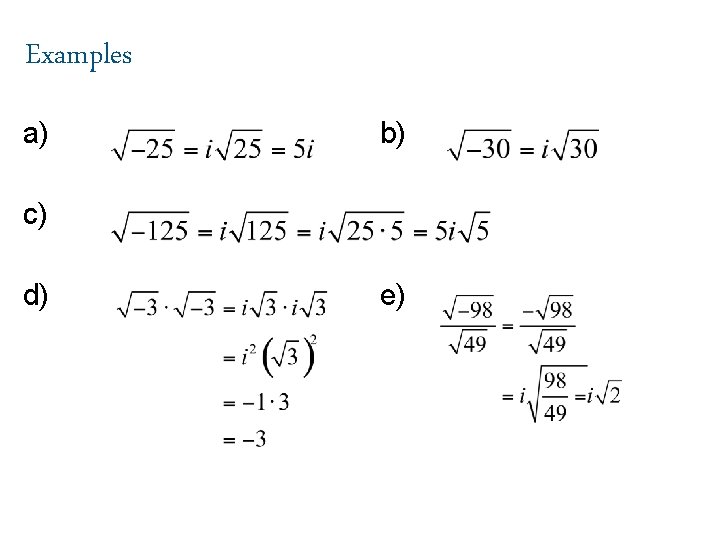
Examples a) b) c) d) e)

Example: Solving Quadratic Equations Solve x = √-25 Take the square root on both sides. The solution set is {± 5 i}.

Another Example Solve: x 2 + 54 = 0 The solution set is

Example: Products and Quotients § Multiply: § Divide:

Addition and Subtraction of Complex Numbers For complex numbers a + bi and c + di, Examples (4 − 6 i) + (− 3 + 7 i) = [4 + (− 3)] + [− 6 + 7]i =1+i (10 − 4 i) − (5 − 2 i) = (10 − 5) + [− 4 − (− 2)]i = 5 − 2 i

Multiplication of Complex Numbers For complex numbers a + bi and c + di, The product of two complex numbers is found by multiplying as if the numbers were binomials and using the fact that i 2 = − 1.

Examples: Multiplying (2 − 4 i)(3 + 5 i) (7 + 3 i)2

Powers of i i 1 = i i 5 = i i 9 = i i 2 = − 1 i 6 = − 1 i 10 = − 1 i 3 = −i i 7 = −i i 11 = −i i 4 = 1 i 8 = 1 i 12 = 1 and so on.

Simplifying Examples i 17 i 4 = 1 i 17 = (i 4)4 • i = 1 • i =i i− 4

Property of Complex Conjugates For real numbers a and b, Example (a + bi)(a − bi) = a 2 + b 2. The product of a complex number and its conjugate is always a real number.

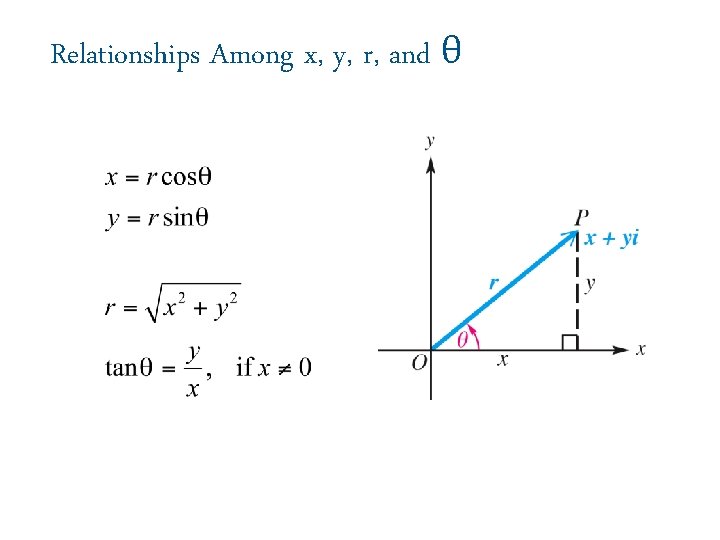
Relationships Among x, y, r, and θ

Trigonometric (Polar) Form of a Complex Number The expression is called the trigonometric form or (polar form) of the complex number x + yi. The expression cos θ + i sin θ is sometimes abbreviated cis θ. Using this notation

Example Express 2(cos 120° + i sin 120°) in rectangular form. Notice that the real part is negative and the imaginary part is positive, this is consistent with 120 degrees being a quadrant II angle.

Converting from Rectangular Form to Trigonometric Form Step 1 Sketch a graph of the number x + yi in the complex plane. Step 2 Find r by using the equation Step 3 Find θ by using the equation choosing the quadrant indicated in Step 1.

Example: Find trigonometric notation for − 1 − i. § First, find r. § Thus,

Product Theorem § If complex numbers, then § In compact form, this is written are any two

Example: Product § Find the product of

Quotient Theorem § If are any two complex numbers, where then

Example: Quotient § Find the quotient.

De Moivre’s Theorem § If is a complex number, and if n is any real number, then § In compact form, this is written

Example: Find (− 1 − i)5 and express the result in rectangular form. § First, find trigonometric notation for − 1 − i § Theorem

nth Roots § For a positive integer n, the complex number a + bi is an nth root of the complex number x + yi if

nth Root Theorem § If n is any positive integer, r is a positive real number, and θ is in degrees, then the nonzero complex number r(cos θ + i sin θ) has exactly n distinct nth roots, given by where

Example: Square Roots §

Example: Fourth Root § Find all fourth roots of roots in rectangular form. § Write in trigonometric form. Write the § Here r = 16 and θ = 120°. The fourth roots of this number have absolute value

Example: Fourth Root continued § There are fourth roots, let k = 0, 1, 2 and 3. § Using these angles, the fourth roots are

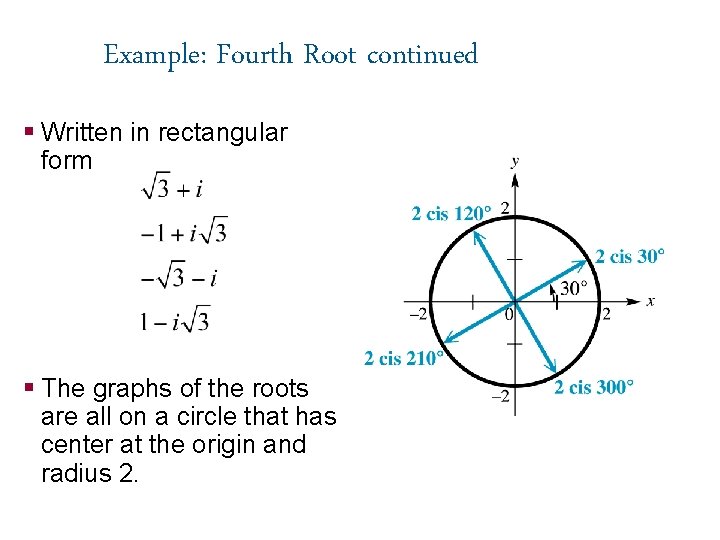
Example: Fourth Root continued § Written in rectangular form § The graphs of the roots are all on a circle that has center at the origin and radius 2.

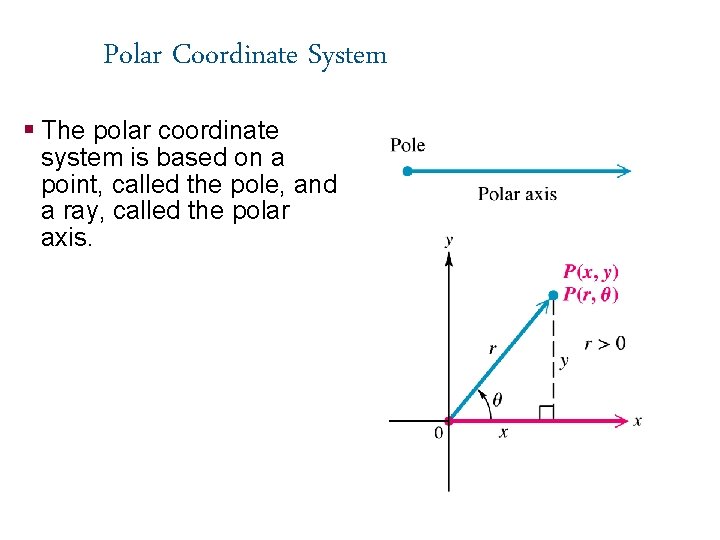
Polar Coordinate System § The polar coordinate system is based on a point, called the pole, and a ray, called the polar axis.

Rectangular and Polar Coordinates § If a point has rectangular coordinates (x, y) and polar coordinates (r, θ), then these coordinates are related as follows.

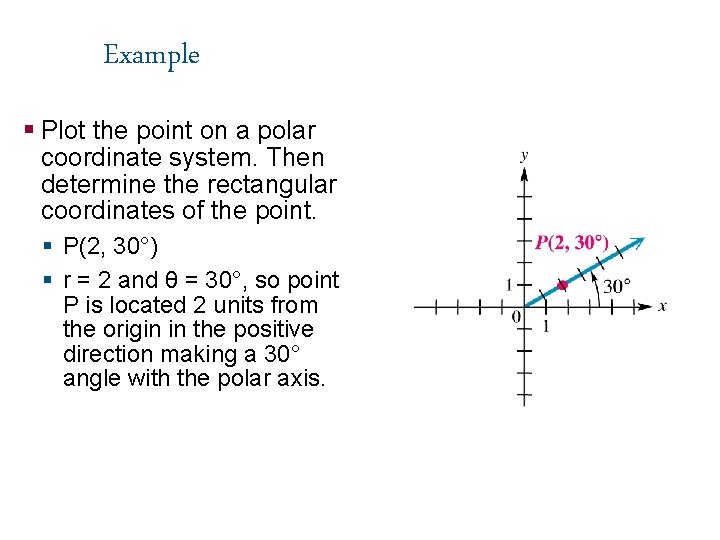
Example § Plot the point on a polar coordinate system. Then determine the rectangular coordinates of the point. § P(2, 30°) § r = 2 and θ = 30°, so point P is located 2 units from the origin in the positive direction making a 30° angle with the polar axis.

Example continued § Using the conversion formulas: § The rectangular coordinates are

Example § Convert (4, 2) to polar coordinates.

The following slides are extension work for Complex Numbers …. .

Rectangular and Polar Equations § To convert a rectangular equation into a polar equation, use and solve for r. For the linear equation you will get the polar equation

Example § Convert x + 2 y = 10 into a polar equation. x + 2 y = 10

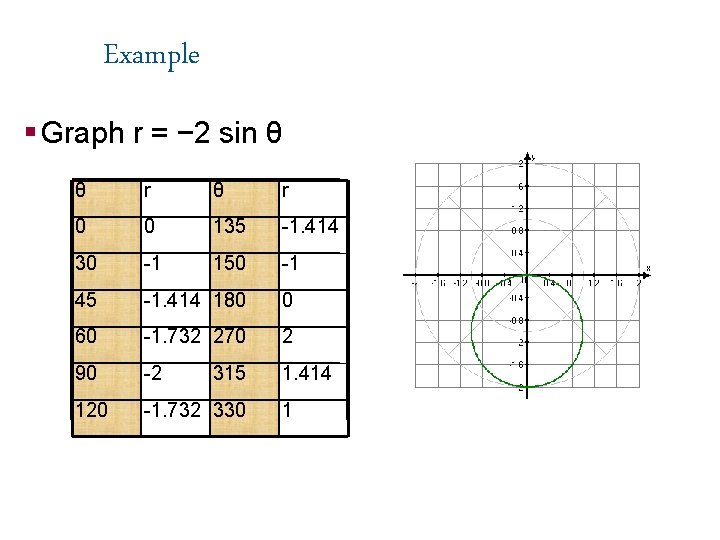
Example § Graph r = − 2 sin θ θ r 0 0 135 -1. 414 30 -1 150 -1 45 -1. 414 180 0 60 -1. 732 270 2 90 -2 1. 414 120 -1. 732 330 315 1

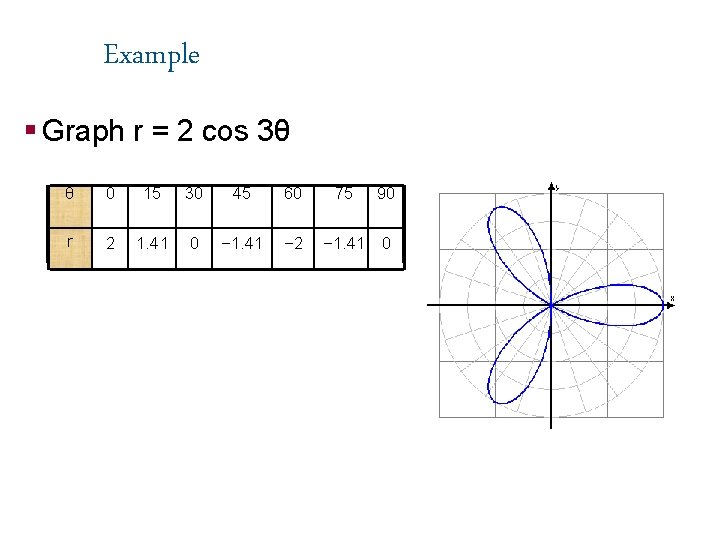
Example § Graph r = 2 cos 3θ θ 0 15 30 45 60 r 2 1. 41 0 − 1. 41 − 2 75 90 − 1. 41 0

Example § Convert r = − 3 cos θ − sin θ into a rectangular equation. §

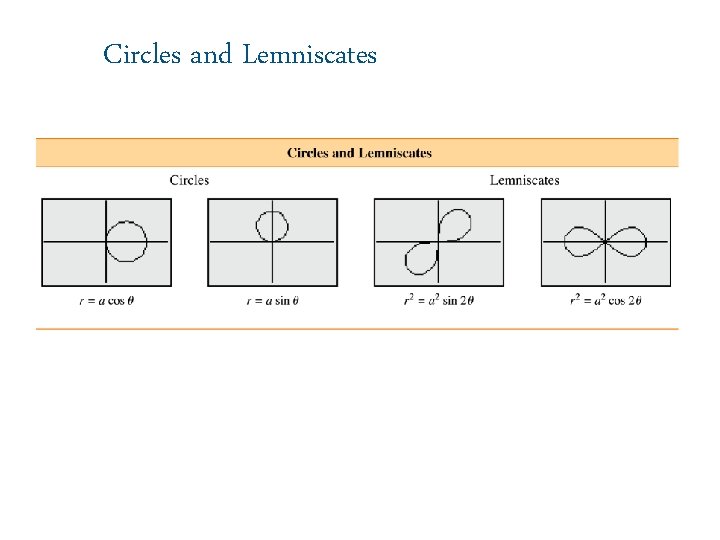
Circles and Lemniscates

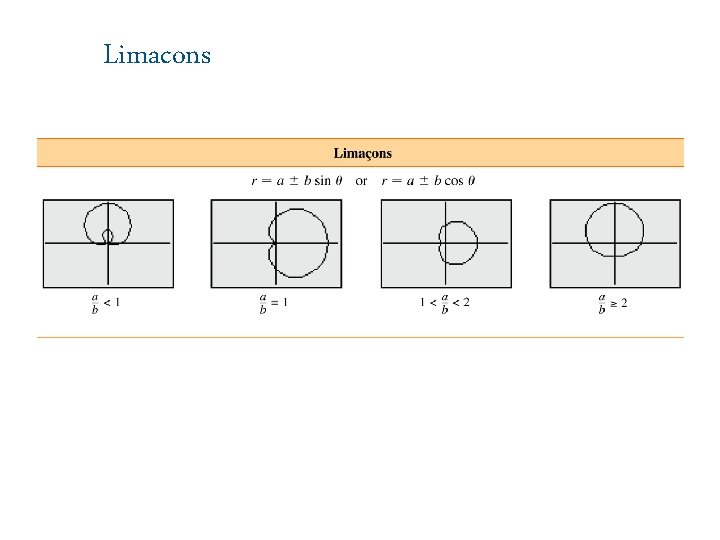
Limacons

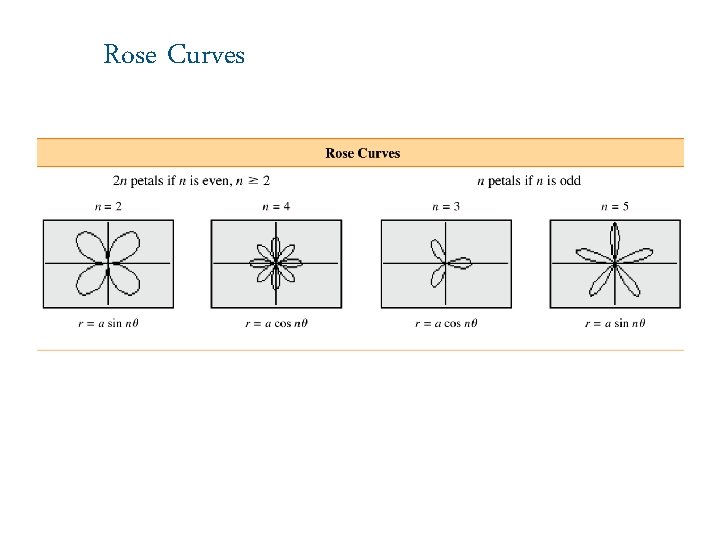
Rose Curves