Complex Numbers 1 August 2006 Definition A complex

Complex Numbers 1 August 2006

Definition • A complex number z is a number of the form where • x is the real part and y the imaginary part, written as x = Re z, y = Im z. • j is called the imaginary unit • If x = 0, then z = jy is a pure imaginary number. • The complex conjugate of a complex number, z = x + jy, denoted by z* , is given by z* = x – jy. • Two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal. 1 August 2006 2

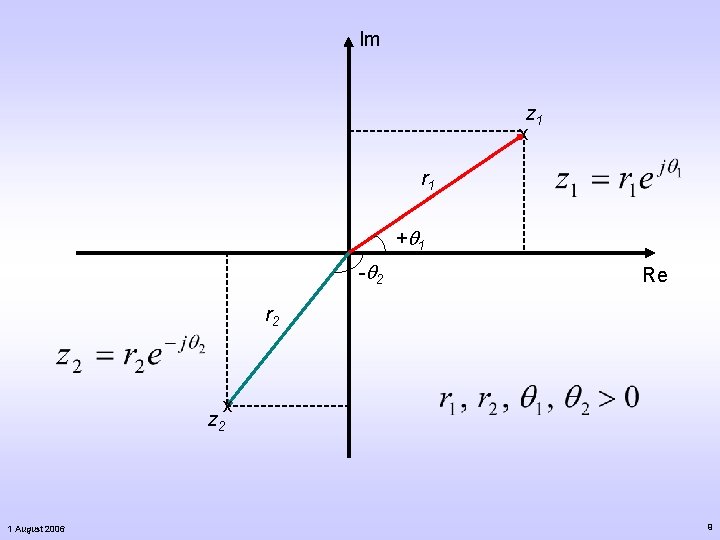
Complex Plane A complex number can be plotted on a plane with two perpendicular coordinate axes l The horizontal x-axis, called the real axis l The vertical y-axis, called the imaginary axis Represent z = x + jy geometrically as the point P(x, y) in the x-y plane, or as the vector from the origin to P(x, y). The complex plane 1 August 2006 x-y plane is also known as the complex plane. 3

Polar Coordinates With z takes the polar form: r is called the absolute value or modulus or magnitude of z and is denoted by |z|. Note that : 1 August 2006 4

Complex plane, polar form of a complex number Geometrically, |z| is the distance of the point z from the origin while θ is the directed angle from the positive xaxis to OP in the above figure. From the figure, 1 August 2006 5

θ is called the argument of z and is denoted by arg z. Thus, For z = 0, θ is undefined. A complex number z ≠ 0 has infinitely many possible arguments, each one differing from the rest by some multiple of 2π. In fact, arg z is actually The value of θ that lies in the interval (-π, π] is called the principle argument of z (≠ 0) and is denoted by Arg z. 1 August 2006 6

Euler Formula – an alternate polar form The polar form of a complex number can be rewritten as : This leads to the complex exponential function : Further leads to : 1 August 2006 7

In mathematics terms, q is referred to as the argument of z and it can be positive or negative. In engineering terms, q is generally referred to as phase of z and it can be positive or negative. It is denoted as The magnitude of z is the same both in Mathematics and engineering, although in engineering, there also different interpretations depending on what physical system one is referring to. Magnitudes are always > 0. The application of complex numbers in engineering will be dealt with later. 1 August 2006 8

Im z 1 x r 1 +q 1 -q 2 Re r 2 x z 2 1 August 2006 9

Example 1 A complex number, z = 1 + j , has a magnitude and argument : Hence its principal argument is : rad Hence in polar form : 1 August 2006 10

Example 2 A complex number, z = 1 - j , has a magnitude and argument : Hence its principal argument is : rad Hence in polar form : In what way does the polar form help in manipulating complex numbers? 1 August 2006 11

Other Examples What about z 1=0+j, z 2=0 -j, z 3=2+j 0, z 4=-2? 1 August 2006 12

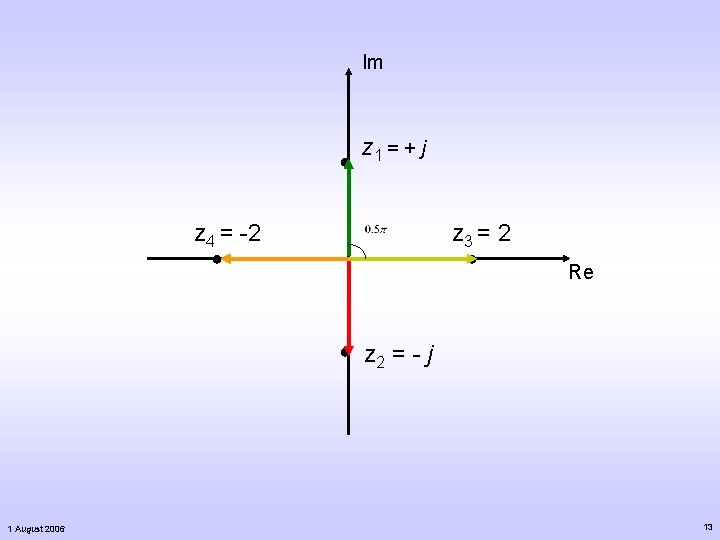
Im ● z 1 = + j z 4 = -2 z 3 = 2 ● ● ● 1 August 2006 Re z 2 = - j 13

Arithmetic Operations in Polar Form • The representation of z by its real and imaginary parts is useful for addition and subtraction. • For multiplication and division, representation by the polar form has apparent geometric meaning. 1 August 2006 14

Suppose we have 2 complex numbers, z 1 and z 2 given by : Easier with normal form than polar form Easier with polar form than normal form magnitudes multiply! 1 August 2006 phases add! 15

For a complex number z 2 ≠ 0, magnitudes divide! 1 August 2006 phases subtract! 16

A common engineering problem involving complex numbers Given the transfer function model : Generally, this is a frequency response model if s is taken to be. In Engineering, you are often required to plot the frequency response with respect to the frequency, w. 1 August 2006 17

For a start : Let’s calculate H(s) at s=j 10. Im Re 2 x 1 August 2006 18

Let’s calculate H(s) at s=j 1. Im Re 2 x x 1 August 2006 19

What happens when the frequency tends to infinity? When the frequency tends to infinity, H(s) tends to zero in magnitude and the phase tends to -900! 1 August 2006 20

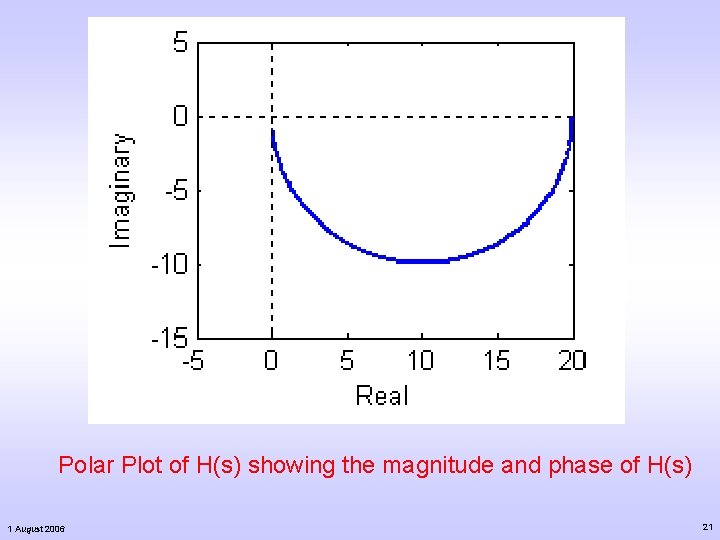
Polar Plot of H(s) showing the magnitude and phase of H(s) 1 August 2006 21

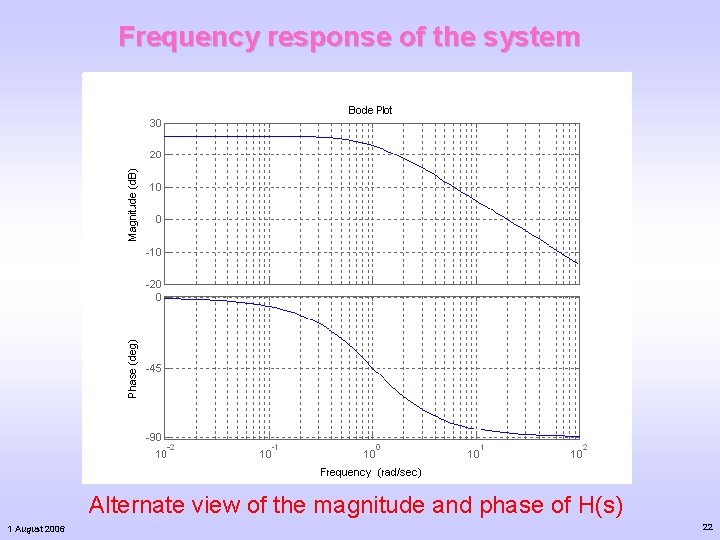
Frequency response of the system Alternate view of the magnitude and phase of H(s) 1 August 2006 22