Complex Numbers 1 a bi We can add

Complex Numbers 1 a + bi

We can add, subtract, multiply or divide complex numbers. After performing these operations if we’ve simplified everything correctly we should always again get a complex number (although the real or imaginary parts may be zero). Below is an example of each to refresh your memory. ADDING SUBTRACTING (3 – 2 i) + (5 – 4 i) = 8 – 6 i (3 – 2 i) - (5 – 4 i) 3 – 2 i - 5 + 4 i = -2 +2 i MULTIPLYING (3 – 2 i) (5 – 4 i) = 15 – 12 i – 10 i+8 i 2 =15 – 22 i +8(-1) = 7 – 22 i Combine real parts and combine imaginary parts Be sure to distribute the negative through before combining real parts and imaginary parts FOIL and then combine like terms. Remember i 2 = -1 Notice when I’m done simplifying that I only have two terms, a real term and an imaginary one. If I have more than that, I need to simplify more.

DIVIDING FOIL Combine like terms Recall that to divide complex numbers, you multiply the top and bottom of the fraction by the conjugate of the bottom. This means the same complex number, but with opposite sign on the imaginary term We’ll put the 41 under each term so we can see the real part and the imaginary part

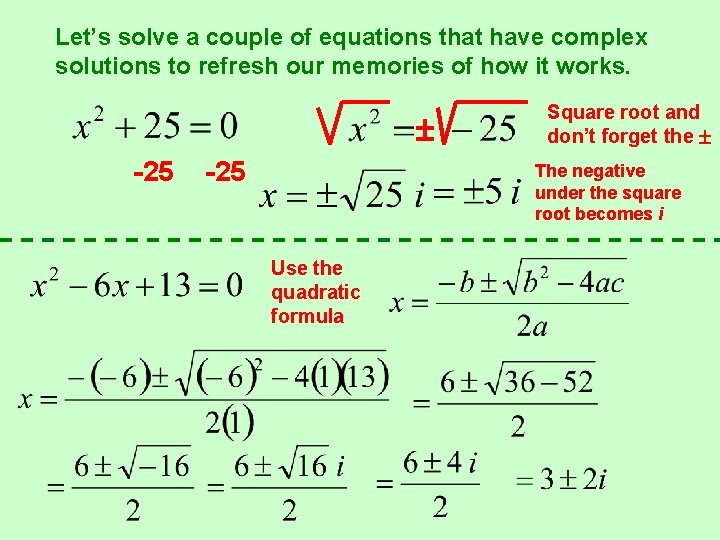
Let’s solve a couple of equations that have complex solutions to refresh our memories of how it works. -25 Square root and don’t forget the The negative under the square root becomes i Use the quadratic formula

Powers of i We could continue but notice that they repeat every group of 4. For every i 4 it will = 1 To simplify higher powers of i then, we'll group all the i 4 ths and see what is left. 4 will go into 33 8 times with 1 left. 4 will go into 83 20 times with 3 left.

This "discriminates" or tells us what type of solutions we'll have. If we have a quadratic equation and are considering solutions from the complex number system, using the quadratic formula, one of three things can happen. 1. The "stuff" under the square root can be positive and we'd get two unequal real solutions 2. The "stuff" under the square root can be zero and we'd get one solution (called a repeated or double root because it would factor into two equal factors, each giving us the same solution). 3. The "stuff" under the square root can be negative and we'd get two complex solutions that are conjugates of each other. The "stuff" under the square root is called the discriminant. The Discriminant