Complex Networks Anurag Singh 1 Complex systems Made

Complex Networks Anurag Singh 1

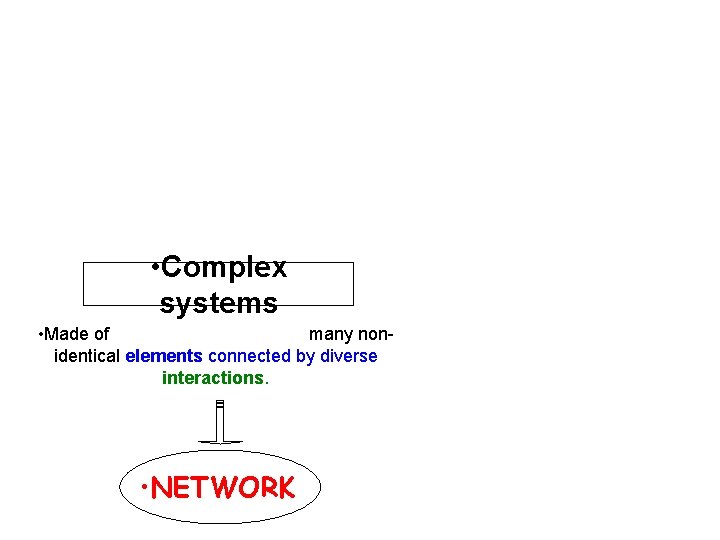
• Complex systems • Made of many nonidentical elements connected by diverse interactions. • NETWORK

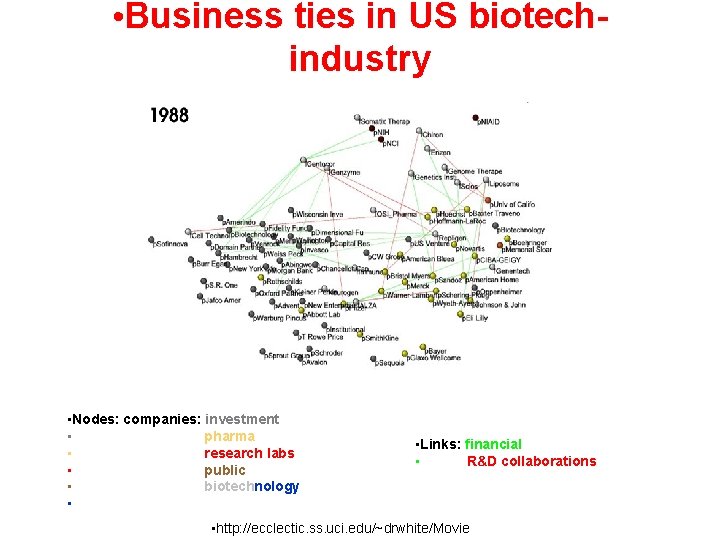
• Business ties in US biotechindustry • Nodes: companies: investment • pharma • research labs • public • biotechnology • • Links: financial • R&D collaborations • http: //ecclectic. ss. uci. edu/~drwhite/Movie

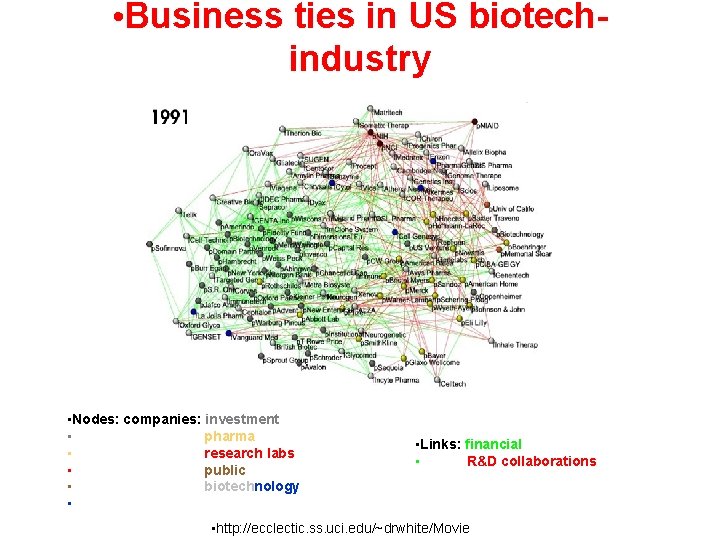
• Business ties in US biotechindustry • Nodes: companies: investment • pharma • research labs • public • biotechnology • • Links: financial • R&D collaborations • http: //ecclectic. ss. uci. edu/~drwhite/Movie

• Structure of an organization • Red, blue, or green: departments • Yellow: consultants • Grey: external experts • www. orgnet. com

• Internet

• Friendship Network

• Network Collaboration Network

• 9 -11 Terrorist (? ) Network • Social Network Analysis is a mathematical methodology for connecting the dots -using science to fight terrorism. Connecting multiple pairs of dots soon reveals an emergent network of organization.

• Some interesting Problems • Consonants (Language) Networks • Marriage Networks • Collaboration Networks • Build Networks which are robust as well as efficient • Actors Network

• Outline • Techniques to analyze networks • Special types of networks – random networks, power law networks, small world networks • Models of network growth • Processes taking place on network – search,

• Traditional vs. Complex Systems Approaches to Networks • Traditional Questions: • Social Networks: • Who is the most important person in the network? • Complex Systems Questions: • Graph Theory: • Does there exist a cycle through the network that uses each edge exactly once? • What fraction of edges have to be removed to disconnect the graph? • What kinds of structures emerge from simple growth rules?

Introduction to Complex Networks • Complex network is a network (graph) with non-trivial topological features (heavy tail in the degree distribution, a high clustering coefficient, assortavity among vertices, and community structure) • Features that do not occur in simple networks • Lattices or random graphs, does not have these features. . Lattice • degree dist. • clustering • assortativity • comunity Random 13

Introduction to Complex Networks (contd. . ) • Many systems in nature can be described by models of complex networks • Structures consisting of nodes or vertices connected by links or edges. 14

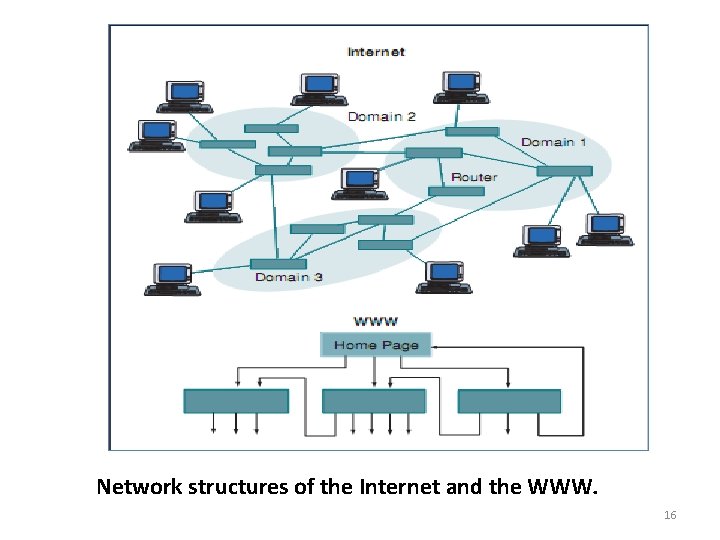
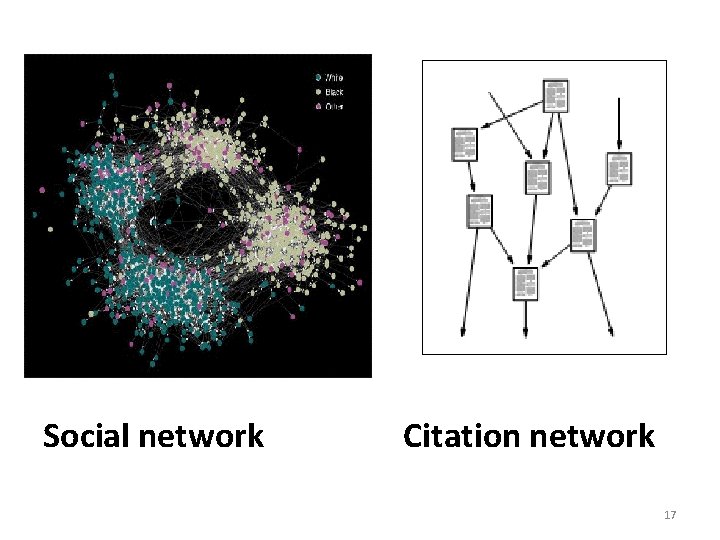
Introduction to Complex Networks (contd. . ) • Examples : – The Internet is a network of routers or domains. – The World Wide Web (WWW) is a network of websites – The brain is a network of neurons. – Social network – Citation networks – Diseases are transmitted through social networks – Man-made infrastructures, and in many physical systems such as the power grids. 15

Network structures of the Internet and the WWW. 16

Social network Citation network 17

Evolution of Complex Network research • Erdös and Rényi (ER) described a network with complex topology by a random graph • Many real-life complex networks are neither completely regular nor completely random, • Two significant recent discoveries are smallworld effect and the scale-free nature of most complex networks. 18

Introduction to Complex Networks (Contd. . ) • Watts and Strogatz (WS) introduced the concept of small-world phenomenon • A prominent common feature of the ER random graph and the WS small-world model is – The connectivity distribution of a network peaks at an average value and decays exponentially. – Each node has about the same number of link connections. – Such networks are called “exponential networks” or “homogeneous networks, ” 19

Introduction to Complex Networks (Contd. . ) • A significant recent discovery in the complex networks is the observation that many largescale complex networks are scale-free, • That is, their connectivity distributions are in a power-law form that is independent of the network scale. • Differs from an exponential network, • A scale-free network is inhomogeneous in nature • Most nodes have very few link connections and yet a few nodes have many connections. 20

Decision parameters and its definitions • Average path length • Clustering coefficient • Degree distribution – Degree exponent 21

Decision parameters and its definitions (contd. . ) Average Path Length • In a network, the distance dij between two nodes, labeled i and j respectively, is defined as the number of edges along the shortest path connecting them. The diameter D: of a network, therefore, is defined to be the maximal distance among all distances between any pair of nodes in the network. • The average path length L of the network, then, is defined as the mean distance between two nodes, averaged over all pairs of nodes. 22

Decision parameters and its definitions (contd. . ) • L determines the effective “size” of a network, • The average path length of most real complex networks is relatively small. ] D = max l (A, B) 23

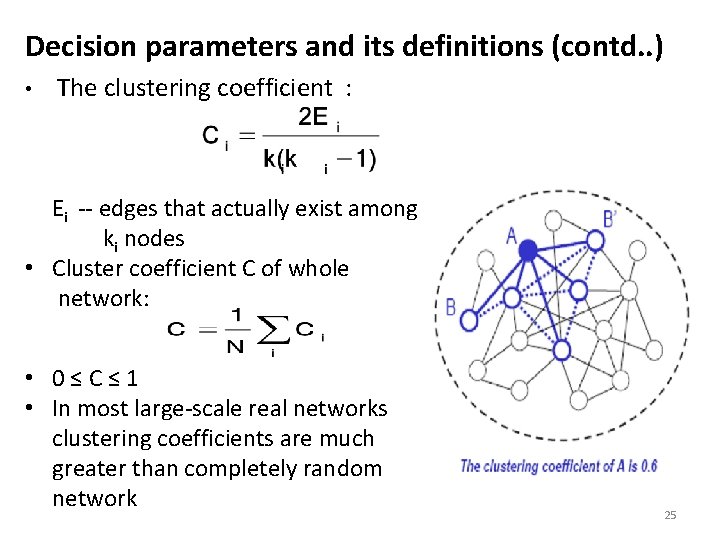
Decision parameters and its definitions (contd. . ) Clustering Coefficient • Two of our friends are quite possibly friends of each other. • This property refers to the clustering of the network. • A clustering coefficient C as the average fraction of pairs of neighbors of a node that are also neighbors of each other. – a node i in the network has ki edges – they connect this node to ki other nodes (neighbors). – at most ki (ki − 1)/2 edges can exist among them 24

Decision parameters and its definitions (contd. . ) • The clustering coefficient : Ei -- edges that actually exist among ki nodes • Cluster coefficient C of whole network: • 0 ≤ C ≤ 1 • In most large-scale real networks clustering coefficients are much greater than completely random network 25

Decision parameters and its definitions (contd. . ) Degree Distribution • The degree ki of a node i is the total number of its neighbors. • The larger the degree, the “more important” the node is in a network. • The average of ki over all i is called the average degree of the network ( < k >). • The spread of node degrees over a network is characterized by a distribution function P(k) • P(k) is the probability that a randomly selected node has exactly k edges. 26

• A regular lattice has a simple degree sequence because all the nodes have the same number of edges – so a plot of the degree distribution contains a single sharp spike • Any randomness in the network will broaden the shape of this peak. In the limiting case of a completely random network – the degree sequence obeys the familiar Poisson distribution – the shape of the Poisson distribution falls off exponentially away from the peak value <k> 27

Small World Networks 28

Duncan J. Watts Six degrees - the science of a connected age, 2003, W. W. Norton. I read somewhere that everybody on this planet is separated by only six other people. Six degrees of separation between us and everybody on this planet. Six degrees of separation by John Guare 29

Correct question WHY are there short chains of acquaintances linking together arbitrary pairs of strangers? ? ? Or � Why is this surprising 31

Random networks In a random network, if everybody has 100 friends distributed randomly in the world population, this isn’t strange In 6 hops, you can reach 1006 people - a million > 6, 000 million (world pop. ) BUT: our social networks tend to be clustered. 32

Social networks Not random But Clustered Most of our friends come from our geographical or professional neighbourhood. Our friends tend to have the same friends BUT In spite of having clustered social networks, there seem to exist short paths between any random nodes. 33

Social network research Devise various classes of networks Study their properties 34

Network parameters Network type Regular Random Natural � � � Size: # of nodes Number of connexions: average & distribution � Selection of neighbours 35

REGULAR Network Topologies STAR TREE GRID BUS RING 36

Connectivity in Random graphs Nodes connected by links in a purely random fashion How large is the largest connected component? (as a fraction of all nodes) Depends on the number of links per node � (Erdös, Rényi 1959) 37

Connecting Nodes 38

Random Network (1) add random • paths 39

Random Network (2) • paths • trees 40

Random Network (3) • paths • trees • networks 41

Random Network (3+) • paths • trees • networks …. . 42

Network Connectivity (4) • paths • trees • networks • fully connected 43

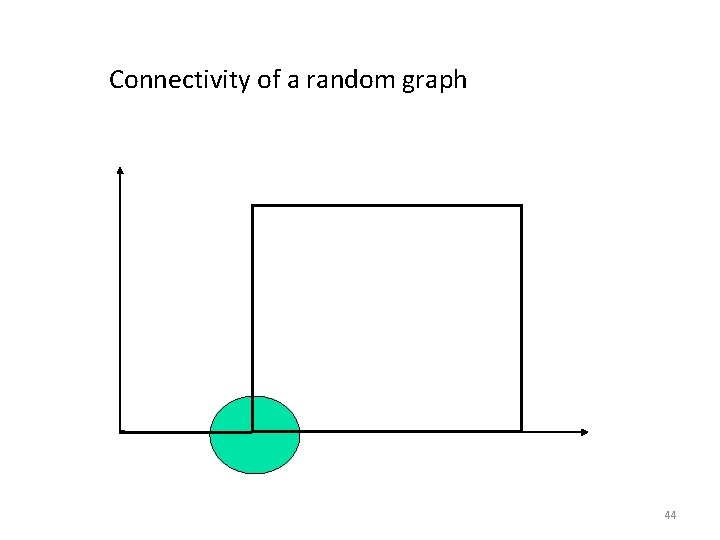
Connectivity of a random graph Conected phase Average number of links per node 1 0 Disconnected phase Fraction of all nodes in largest component 1 44

Regular or Ordered Network 45

Network measures Connectivity is not main measure. Characteristic Path Length (L) : the average length of the shortest path connecting each pair of agents (nodes). � Clustering Coefficient (C) is a measure of local interconnection if agent i has ki immediate neighbors, Ci, is the fraction of the total possible ki*(ki-1) / 2 connections that are realized between i's neighbors. C, is just the average of the Ci's. � Diameter: maximum value of path length 46

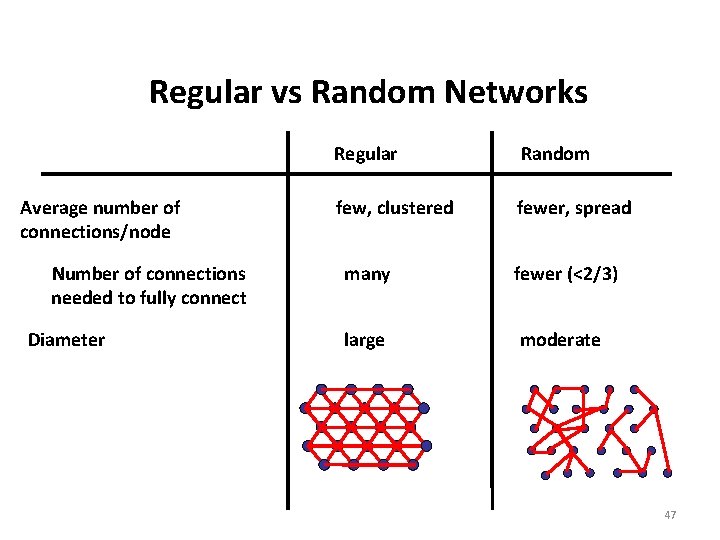
Regular vs Random Networks Average number of connections/node Number of connections needed to fully connect Diameter Regular Random few, clustered fewer, spread many fewer (<2/3) large moderate 47

Classes of Complex Networks 1. Random Graphs Model • First studied by Erdos and Renyi • Some properties of E-R networks: if nodes in in graph = N Average number of edges (= size of graph): Let n , vertices and connect each pair (or not) with probability p (or 1 -p). � E = p N (N - 1) / 2 Average degree: 〈k〉 = 2 E/N = p (N - 1) ~ p N 48

Classes of Complex Networks (contd. . ) • Erdos and Renyi proposed the following model of a network : • the model called Gn, p , is the ensemble of all such graphs in which a graph having m edges appears with pm(1 -p)M-m, where , , is the maximum possible number of edges. 49

Classes of Complex Networks (contd. . ) another model, called Gn, m, which is the ensemble of all graphs having n vertices and exactly m edges, each possible graph appearing with equal probability. • presence or absence of edges is independent, and hence the probability of a vertex having degree k is: � (for large n and fixed k) Where, z =expected degree = p(n-1) 50

Classes of Complex Networks (contd. . ) 2. Small world Phenomenon • “Almost every pair of nodes is connected by a path with an extremely small number of steps. ” L<<N for N>>1 • Small-World experiment(1960), by S. Milgram • Having people explicitly construct path through the social network defined by acquaintanceship (firstname basis) • The median length among the completed path was 6 ( six degrees of freedom) 51

Classes of Complex Networks (contd. . ) • For a constant k ≥ 3, if we choose uniformly at random from the set of all n-node graphs in which each node has degree exactly k, then with high probability every pair of nodes will be joined by a path of length O(log n). ( B. Bollobas, W. F. de la Vega. The diameter of random regular graphs. Combinatorica 2 (1982) ) • Path lengths is polylogarithmic in n. (bounded by a polynomial function of log n) 52

There is something missing. . . • Small-world is not only about “short path” • A standard random graph is locally very sparse. • With reasonably high probability, none of the neighbors of a given node v are themselves neighbors of one another. (Watts, D. J. and Strogatz, S. H. , Collective dynamics of ‘smallworld’ networks. Nature (1998)) • Implication → The social Network appears from the local perspective of any one node to be highly clustered. 53

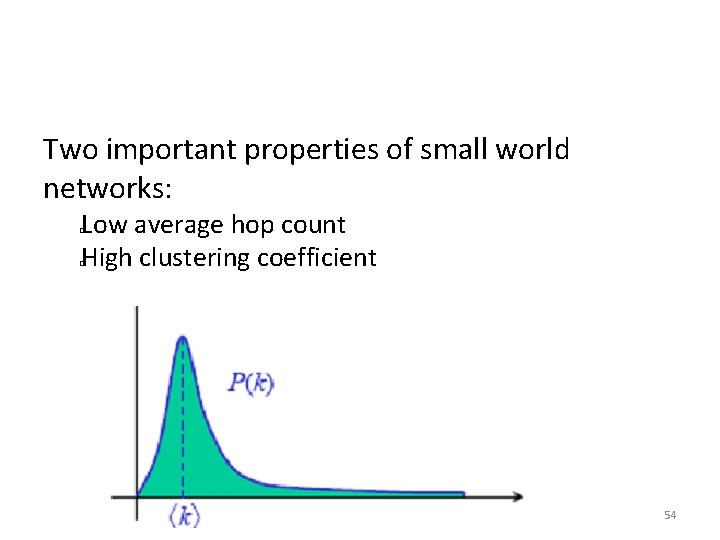
Two important properties of small world networks: Low average hop count High clustering coefficient � � 54

Classes of Complex Networks (contd. . ) Small-World Models • The regular lattice model and the ER random model both fail to reproduce some important features of many real networks. • Most of these real-world networks are neither entirely regular nor entirely random. • People usually know their neighbors, 55

Classes of Complex Networks (contd. . ) Watts-Strogatz Model • Add some “random” links to a structured, high diameter network. Most people are friends with their immediate neighbors Everyone has one or two friends who are far away. � � 56

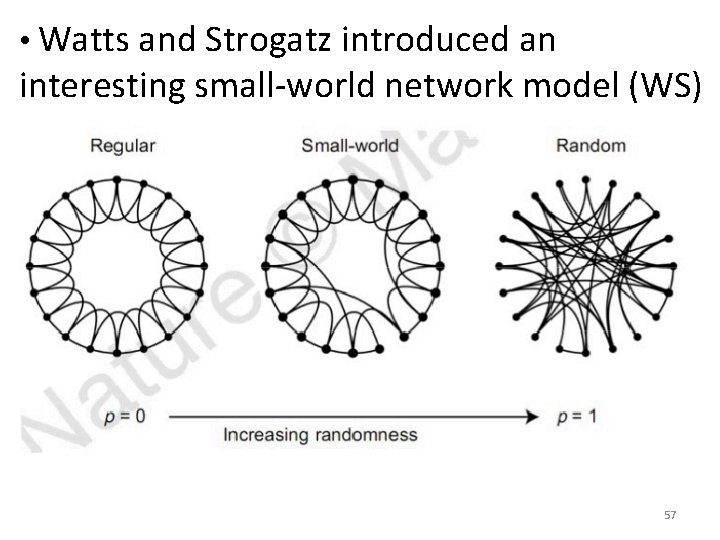
• Watts and Strogatz introduced an interesting small-world network model (WS) as . 57

WS Small-World Model Algorithm 1) Start with regular: Begin with a nearestneighbor coupled network consisting of N nodes arranged in a ring, where each node i is adjacent to its neighbor nodes, i = 1, 2, ··· , K/2, with K being even. 2) Randomization: Randomly rewire each edge of the network with probability p; varying p in such a way that the transition between (p = 0) and randomness (p = 1) can be closely monitored. 58

• Random graphs show the small-world effect, but do not show clustering. • The small-world model can be viewed as a homogeneous network. • the WS small-world network model is similar to the ER random graph model. Analysis of WS Model • C(p) - Clustering coefficient • L(p) - average path length, considered as a function of the rewiring probability p. • A regular ring lattice (p = 0) is : • highly clustered (C (0) ≈ 3/4) • L~ ln N 59

P Fig [Courtesy of NATURE] Average Path Length and clustering coefficient of the WS small-world model 60

Example: 4096 node ring K=4 Regular graph: n nodes, k nearest neighbors path length ~ n/2 k 4096/16 = 256 Rewired graph (1% of nodes): path length ~ random graph clustering ~ regular graph �Small World Graph Random graph: path length ~ log (n)/log(k) ~4 61

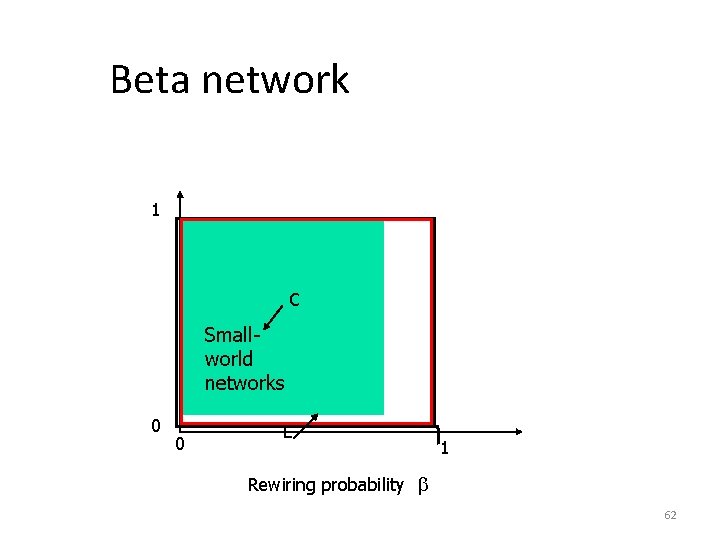
Beta network 1 C Smallworld networks 0 0 L 1 Rewiring probability 62

More exactly …. (p = ) C L Small world behaviour 63

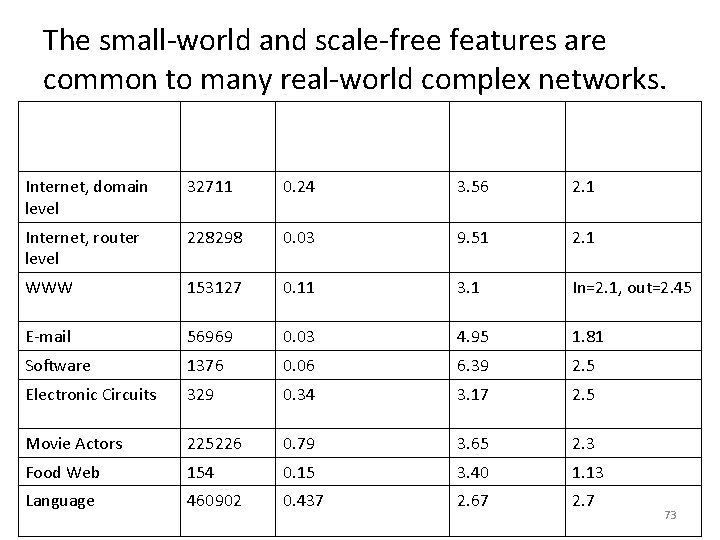
The small-world and scale-free features are common to many real-world complex networks. Network Size Clustering Coefficient Average path length Degree exponent Internet, domain level 32711 0. 24 3. 56 2. 1 Internet, router level 228298 0. 03 9. 51 2. 1 WWW 153127 0. 11 3. 1 In=2. 1, out=2. 45 E-mail 56969 0. 03 4. 95 1. 81 Software 1376 0. 06 6. 39 2. 5 Electronic Circuits 329 0. 34 3. 17 2. 5 Movie Actors 225226 0. 79 3. 65 2. 3 Food Web 154 0. 15 3. 40 1. 13 Language 460902 0. 437 2. 67 2. 7

Effect of short-cuts Huge effect of just a few short-cuts. First 5 rewirings reduces the path length by half, regardless of size of network Further 50% gain requires 50 more shortcuts 65

The strength of weak ties Granovetter (1973): effective social coordination does not arise from densely interlocking strong ties, but derives from the occasional weak ties this is because valuable information comes from these relations (it is valuable if/because it is not available to other individuals in your immediate network) � 66

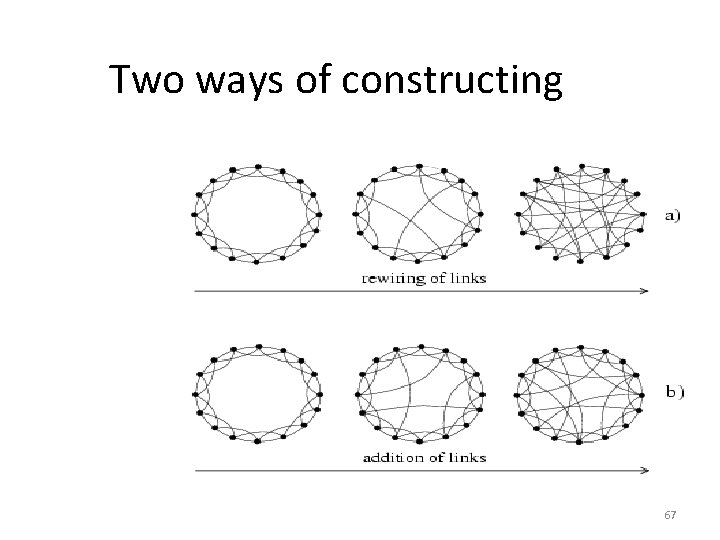
Two ways of constructing 67

Alpha model Watts’ first Model (1999) Inspired by Asimov’s “I, Robot” novels R. Daneel Olivaw Elijah Baley � � Caves of Steel (Earth) Solaria 68

Natural networks Between regular grids and totally random graphs Need for parametrized models: Regular -> natural -> random � Watts Alpha model ( not intuitive) Beta rewiring model � � � 69

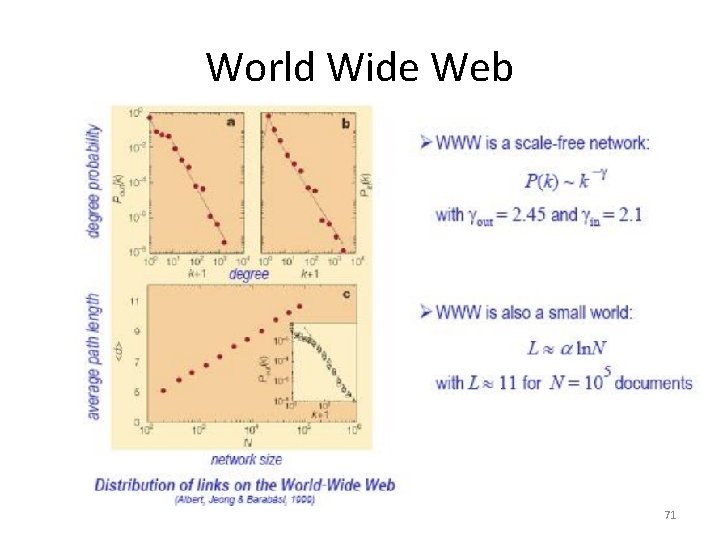
Applications Social Network of movie actors • Two actors being connected if they were cast together in the same movie. • The probability that an actor has k links (characterizing his or her popularity) has a power-law tail for large k, : P(k) ~k-Уactor , where , Уactor = 2. 3 ± 0. 1 C=0. 79, L = 3. 65 • so, it also follows the small world property as well as scale free network. A more complex network with over 800 million 70

World Wide Web 71

The electrical power grid • the vertices being generators , transformers, and substations • the edges being to the high-voltage transmission lines • For 4941 vertices : • Уpower = 4 • L = 18. 99 • C=0. 10 72

The small-world and scale-free features are common to many real-world complex networks. Network Size Clustering Coefficient Average path Degree length exponent Internet, domain level 32711 0. 24 3. 56 2. 1 Internet, router level 228298 0. 03 9. 51 2. 1 WWW 153127 0. 11 3. 1 In=2. 1, out=2. 45 E-mail 56969 0. 03 4. 95 1. 81 Software 1376 0. 06 6. 39 2. 5 Electronic Circuits 329 0. 34 3. 17 2. 5 Movie Actors 225226 0. 79 3. 65 2. 3 Food Web 154 0. 15 3. 40 1. 13 Language 460902 0. 437 2. 67 2. 7 73

Some more Applications Areas Real-World Applications • Peer-to-Peer File-sharing System • find a file <=> find a person • Focused Web Crawling • how to efficiently find a webpage? • Social Network Data • Is naturally occurring networks organized in same way? 74

Classes of Complex Networks (contd. . ) 3. Scale-Free Models (Rich get richer) • Number of large-scale complex networks have connectivity distributions have a power-law form are scale free like: the Internet, WWW, and citation networks � � � • The BA model suggests that two main ingredients of a scale-free structure are: growth � 75

Classes of Complex Networks (contd. . ) • In most large-scale real networks the degree distribution deviates significantly from the Poisson distribution. • For a number of networks, the degree distribution can be described by a power law : P(k) ∼ k−γ • Power-law distribution falls off more gradually than an exponential one • Allowing for a few nodes of very large degree to exist. • A network with a power-law degree distribution is called a scale-free network. 76

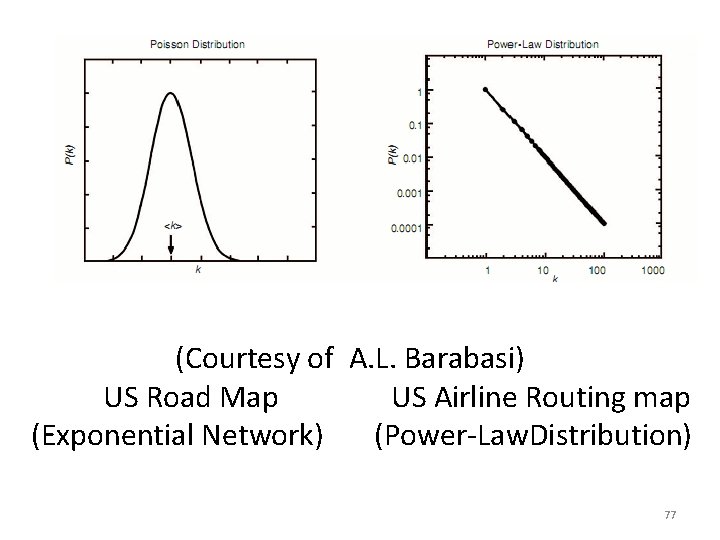
(Courtesy of A. L. Barabasi) US Road Map US Airline Routing map (Exponential Network) (Power-Law. Distribution) 77

Decision parameters and its definitions (contd. . ) Cohen and Havlin proved that uncorrelated power law graphs having 2 < γ < 3 will also have ultrasmall diameter d ~ ln ln N. • So , the diameter of a growing scale-free network might be considered almost constant. • Scale free networks are still small world networks because: (i) they have clustering coefficients much larger than random networks, � 78

BA Scale-Free Model Algorithm 1) Growth: Start with a small number (m 0) of nodes; at every time step, a new node is introduced and is connected to m ≤ m 0 already-existing nodes. 2) Preferential Attachment: The probability Πi that a new node will be connected to node i (one of the m alreadyexisting nodes) depends on the degree ki of node i, in such a way that Πi = ki/ Σjkj. 79

Applications Social Network of movie actors • Two actors being connected if they were cast together in the same movie. • The probability that an actor has k links (characterizing his or her popularity) has a power-law tail for large k, : P(k) ~k-Уactor , where , Уactor = 2. 3 ± 0. 1 C=0. 79, L = 3. 65 • so, it also follows the small world property as well as scale free network. A more complex network with over 800 million 80

Some more Applications Areas Real-World Applications • Peer-to-Peer File-sharing System • find a file <=> find a person • Focused Web Crawling • how to efficiently find a webpage? • Social Network Data • Is naturally occurring networks organized in same way? 81

Bibliography • Reviews Barabási, A. -L. (2002) Linked: The New Science of Networks. Perseus Books. Barabási, A. -L. and Bonabeau, E. (2003) Scale-free networks. Scientific American, 288: 60 -69. Strogatz, S. H. (2001) Exploring complex networks. Nature, 410(6825): 268 -276. Wang, X. F. (2002) Complex networks: topology, dynamics and synchronization. International Journal of Bifurcation and Chaos, 12(5): 885 -916. Newman M. E. J. (2003) The structure and function of complex networks. ar. Xiv: cond-mat/0303516 v 1 � � � 82 52