Complex Networks Analysis Information Systems Engineering 72 2

Complex Networks Analysis Information Systems Engineering 72 -2 -5503 (2013 A) Instructor: Rami Puzis (puzis@bgu. ac. il) TA: Luiza Nahshon (lu. nacshon@gmail. com) Web: https: //piazza. com/bgu. ac. il/fall 2013/3722 5503 Slides are taken in part from Coursera: https: //class. coursera. org/sna-003/class Network Science class 2012 (http: //barabasilab. neu. edu/courses/phys 5116/)

Course schedule Week 1 Topic Introduction, Graph Theory, 2 -3 Properties of networks 4 -7 Centrality measures 8 -9 Community structure 10 -11 Generative models 11 -13 Diffusion in networks

• Exercise 1 (due 31/10/2013) – Find and download four different networks from four different web sites. The web sites should reside in different domains. At least one network should have less than 1, 000 vertices and at least one network should have more than 100, 000 vertices. – Use gephi of other network analysis software for a nice layout of the networks and submit PDF of the network visualization. – Fill the course questioner.

WHY COMPLEX NETWORKS

TRANSPORTATION:

Communication networks domain 2 domain 1 rout er domain 3

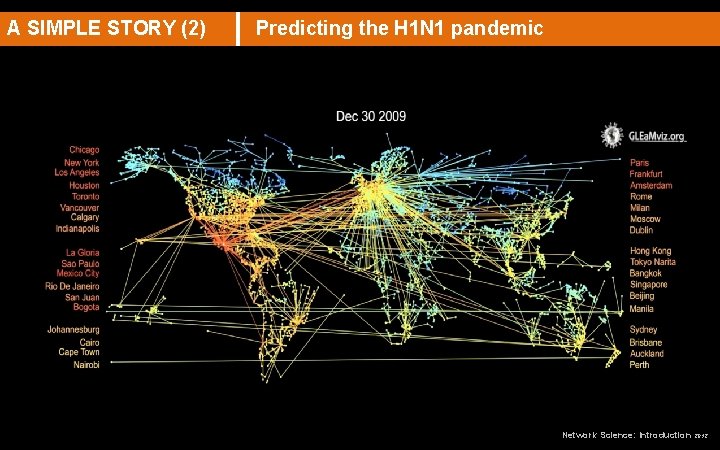
A SIMPLE STORY (2) Predicting the H 1 N 1 pandemic Thex Network Science: Introduction 2012

EPIDEMIC FORECAST Predicting the H 1 N 1 pandemic Real Projected Network Science: Introduction 2012

The August 14, 2003 outage Thex Network Science: Introduction 2012

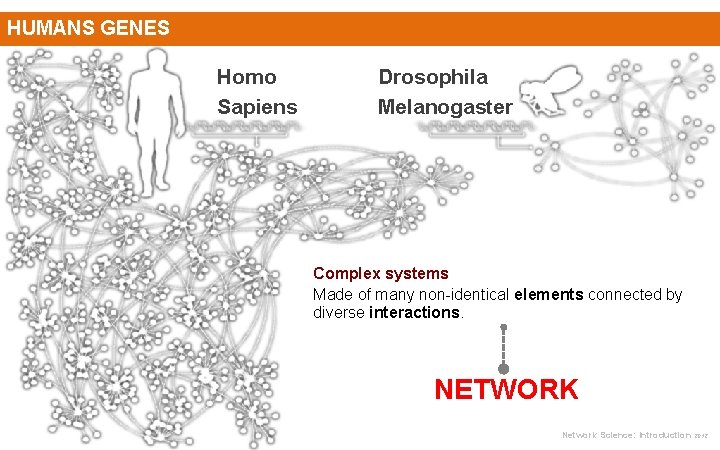
HUMANS GENES Humans have only about three times as many genes as the fly, so human complexity seems unlikely to come from a sheer quantity of genes. Rather, some scientists suggest, each human has a network with different parts like genes, proteins and groups. Network Science: Introduction 2012

HUMANS GENES Homo Sapiens Drosophila Melanogaster Complex systems Made of many non-identical elements connected by diverse interactions. NETWORK Network Science: Introduction 2012

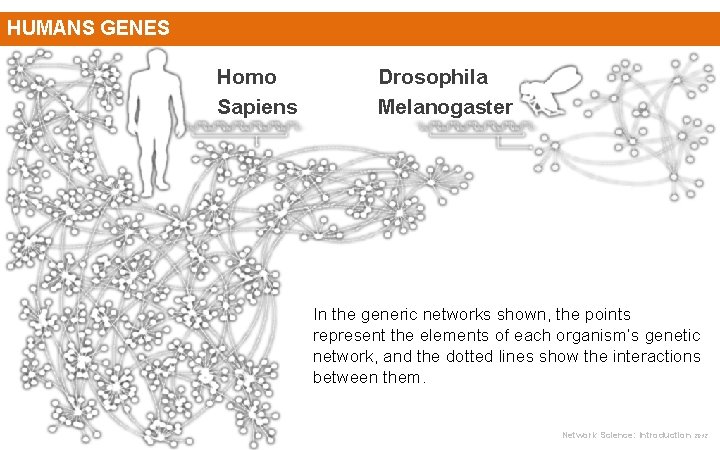
HUMANS GENES Homo Sapiens Drosophila Melanogaster In the generic networks shown, the points represent the elements of each organism’s genetic network, and the dotted lines show the interactions between them. Network Science: Introduction 2012

HARDWARE

SOFTWARE:

Network Science: Introduction 2012

THE LIFE OF NETWORKS Network Science: Introduction 2012

THE HISTORY OF NETWORK ANALYSIS Graph theory: 1735, Euler Social Network Research: 1930 s, Moreno Communication networks/internet: 1960 s Ecological Networks: May, 1979. Network Science: Introduction 2012

NETWORK SCIENCE The science of the 21 st century Network Science: Introduction 2012

THE EMERGENCE OF NETWORK SCIENCE Data Availability: Movie Actor Network, 1998; World Wide Web, 1999. C elegans neural wiring diagram 1990 Citation Network, 1998 Metabolic Network, 2000; PPI network, 2001 Universality: The architecture of networks emerging in various domains of science, nature, and technology are more similar to each other than one would have expected. The (urgent) need to Despite the challenges complex systems offer us, we cannot afford to not address their behavior, a view understand complexity: increasingly shared both by scientists and policy makers. Networks are not only essential for this journey, but during the past decade some of the most important advances towards understanding complexity were provided in context of network theory. Network Science: Introduction 2012

MOST IMPORTANT Networks Really Matter If you were to understand the spread of diseases, can you do it without networks? If you were to understand the WWW structure, Thexsearchability, etc, hopeless without invoking the Web’s topology. If you want to understand human diseases, it is hopeless without considering the wiring diagram of the cell. Network Science: Introduction 2012

GRAPH THEORY AND BASIC TERMINOLOGY

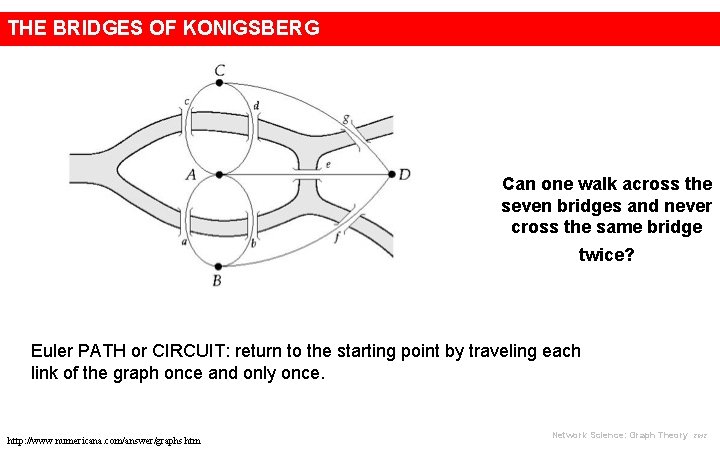
THE BRIDGES OF KONIGSBERG Can one walk across the seven bridges and never cross the same bridge twice? Euler PATH or CIRCUIT: return to the starting point by traveling each link of the graph once and only once. http: //www. numericana. com/answer/graphs. htm Network Science: Graph Theory 2012

COMPONENTS OF A COMPLEX SYSTEM § components: nodes, vertices N § interactions: links, edges L § system: (N, L) network, graph Network Science: Graph Theory 2012

NETWORKS OR GRAPHS? network often refers to real systems • www, • social network • metabolic network. Language: (Network, node, link) graph: mathematical representation of a network • web graph, • social graph (a Facebook term) Language: (Graph, vertex, edge) We will try to make this distinction whenever it is appropriate, but in most cases we will use the two terms interchangeably. Network Science: Graph Theory 2012

A COMMON LANGUAGE friend Mary Peter brothers friend Movie 1 co-worker Albert Movie 2 Albert Protein 1 Actor 2 Actor 1 Movie 3 Actor 4 Actor 3 Protein 2 Protein 5 Protein 9 N=4 L=4 Network Science: Graph Theory 2012

CHOOSING A PROPER REPRESENTATION The choice of the proper network representation determines our ability to use network theory successfully. In some cases there is a unique, unambiguous representation. In other cases, the representation is by no means unique. For example, , the way we assign the links between a group of individuals will determine the nature of the question we can study. Network Science: Graph Theory 2012

CHOOSING A PROPER REPRESENTATION If you connect individuals that work with each other, you will explore the professional network. Network Science: Graph Theory 2012

CHOOSING A PROPER REPRESENTATION If you connect those that have a romantic and sexual relationship, you will be exploring the sexual networks. HOWEVER Could you investigate Sexually Transmitted Diseases without time series data?

CHOOSING A PROPER REPRESENTATION Grey arrows indicate STD propagation chance in one Direction Blue lines indicate STD propagation chance In both directions

CHOOSING A PROPER REPRESENTATION If you connect individuals based on their first name (all Peters connected to each other), you will be exploring what? It is a network, nevertheless. Network Science: Graph Theory 2012

Annotated networks Luis Joe Lea Mia Edna An n Lisa Ted Brad Jim Bob Ben Mary Ellie Mind y Dina Ed Steve

Annotated networks Luis Joe Edna Lea Mia poor average Anna rich Lisa teen Brad old Ted adult Jim adult young Bob Mind y Friend Child Ed Ben Mary Ellie Colleague Dina An n Steve

Network Science: Graph Theory 2012

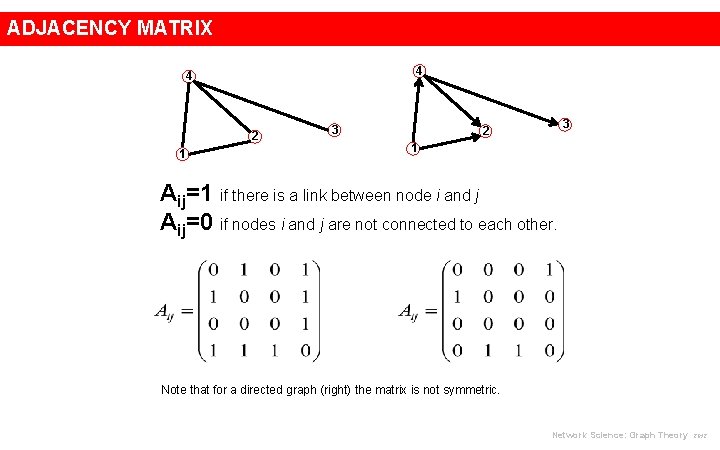
ADJACENCY MATRIX 4 4 2 1 3 3 2 1 Aij=1 if there is a link between node i and j Aij=0 if nodes i and j are not connected to each other. Note that for a directed graph (right) the matrix is not symmetric. Network Science: Graph Theory 2012

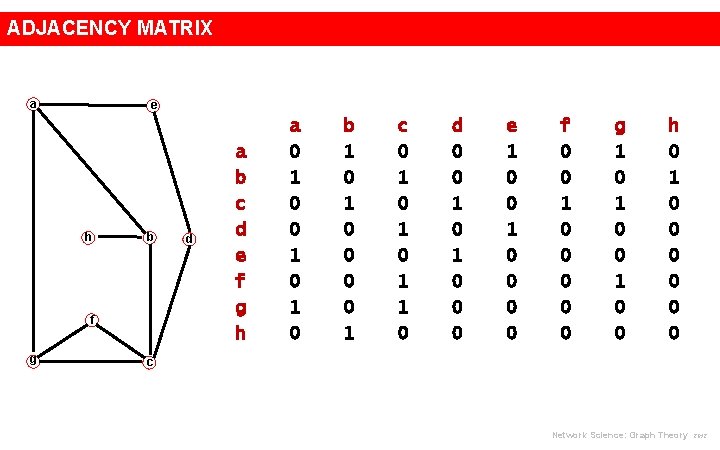
ADJACENCY MATRIX a e h b f g d a b c d e f g h a 0 1 0 1 0 b 1 0 0 0 0 1 c 0 1 0 1 1 0 d 0 0 1 0 0 0 e 1 0 0 0 0 f 0 0 1 0 0 0 g 1 0 0 h 0 1 0 0 0 c Network Science: Graph Theory 2012

GRAPHOLOGY 1 Undirected 4 Directed 1 1 3 4 2 Actor network, protein-protein interactions 3 WWW, citation networks 2 Network Science: Graph Theory 2012

GRAPHOLOGY 2 Unweighted 4 (undirected) Weighted 1 3 4 (undirected) 1 2 protein-protein interactions, www 2 3 Call Graph, metabolic networks Network Science: Graph Theory 2012

What do the numbers mean? 3 Semantics! 3 2 0. 5 2 3 1 2 5 3 2 0. 5 2 Link weights are used to quantify semantics length, strength, capacity, … 1 2 5 Links Weights Road network Distance, capacity Email network Number of emails, size of the emails Coauthoirship Number of publications Network Science: Graph Theory 2012

GRAPHOLOGY 3 Self-interactions 4 1 3 Multigraph (undirected) 1 2 Protein interaction network, www 4 3 2 Social networks, collaboration networks Network Science: Graph Theory 2012

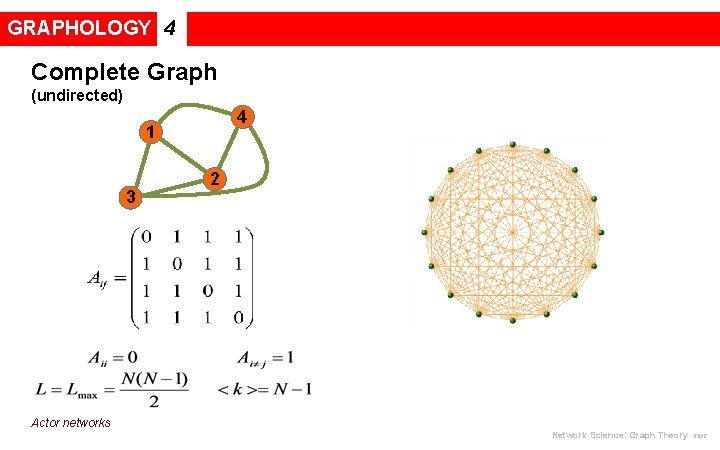
GRAPHOLOGY 4 Complete Graph (undirected) 4 1 3 Actor networks 2 Network Science: Graph Theory 2012

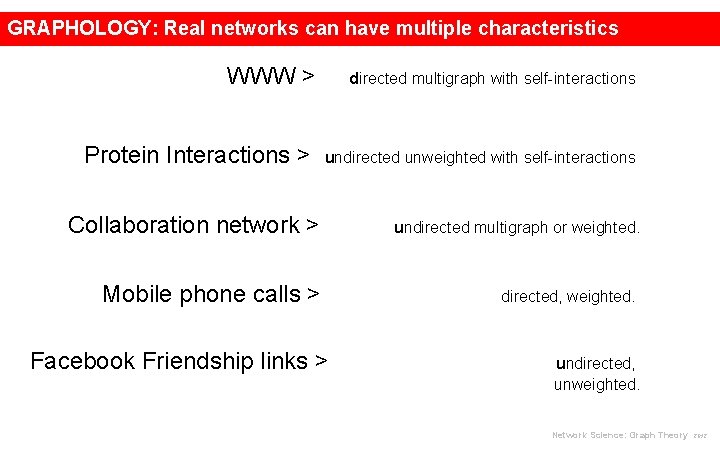
GRAPHOLOGY: Real networks can have multiple characteristics WWW > directed multigraph with self-interactions Protein Interactions > undirected unweighted with self-interactions Collaboration network > undirected multigraph or weighted. Mobile phone calls > directed, weighted. Facebook Friendship links > undirected, unweighted. Network Science: Graph Theory 2012

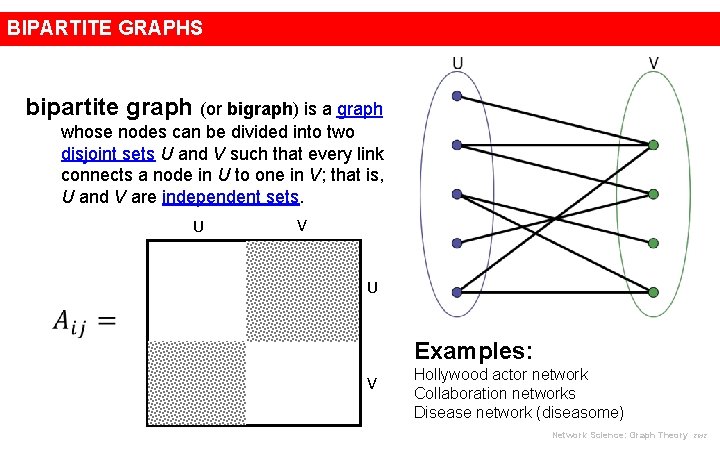
BIPARTITE GRAPHS bipartite graph (or bigraph) is a graph whose nodes can be divided into two disjoint sets U and V such that every link connects a node in U to one in V; that is, U and V are independent sets. U V U Examples: V Hollywood actor network Collaboration networks Disease network (diseasome) Network Science: Graph Theory 2012

GENE NETWORK – DISEASE NETWORK DISEASOME PHENOME Gene network Goh, Cusick, Valle, Childs, Vidal & Barabási, PNAS (2007) Disease network Network Science: Graph Theory 2012

Network Science: Graph Theory 2012

Directed Undirected ADJACENCY MATRIX AND NODE DEGREES 4 3 2 1 4 2 3 1 Network Science: Graph Theory 2012

Directed Undirected NODE DEGREES Node degree: the number of links connected to the node. A B In directed networks we can define an in-degree and out-degree. D B C A The (total) degree is the sum of in- and out-degree. E G F Source: a node with kin= 0; Sink: a node with kout= 0.

A BIT OF STATISTICS We have a sample of values x 1, . . . , x. N Average (a. k. a. mean): typical value <x> = (x 1 +. . . + x. N)/N = Σi xi /N Network Science: Graph Theory 2012

Directed Undirected AVERAGE DEGREE j i N – the number of nodes in the graph D B C E A F Network Science: Graph Theory 2012

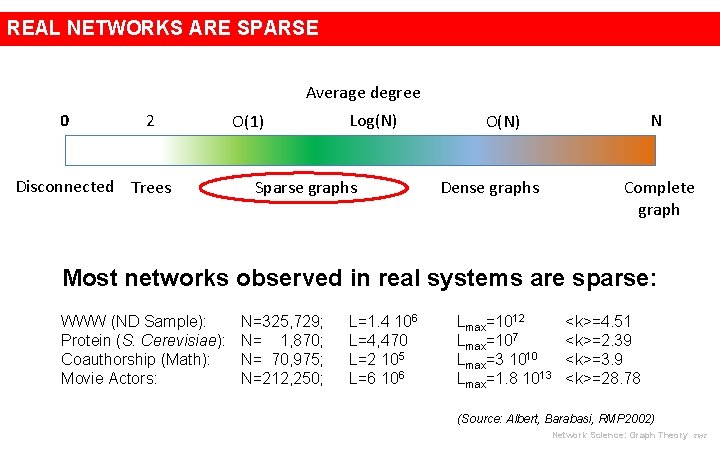
REAL NETWORKS ARE SPARSE Average degree 0 2 Disconnected Trees O(1) Log(N) Sparse graphs N O(N) Dense graphs Complete graph Most networks observed in real systems are sparse: WWW (ND Sample): Protein (S. Cerevisiae): Coauthorship (Math): Movie Actors: N=325, 729; N= 1, 870; N= 70, 975; N=212, 250; L=1. 4 106 L=4, 470 L=2 105 L=6 106 Lmax=1012 Lmax=107 Lmax=3 1010 Lmax=1. 8 1013 <k>=4. 51 <k>=2. 39 <k>=3. 9 <k>=28. 78 (Source: Albert, Barabasi, RMP 2002) Network Science: Graph Theory 2012

Network Science: Graph Theory 2012

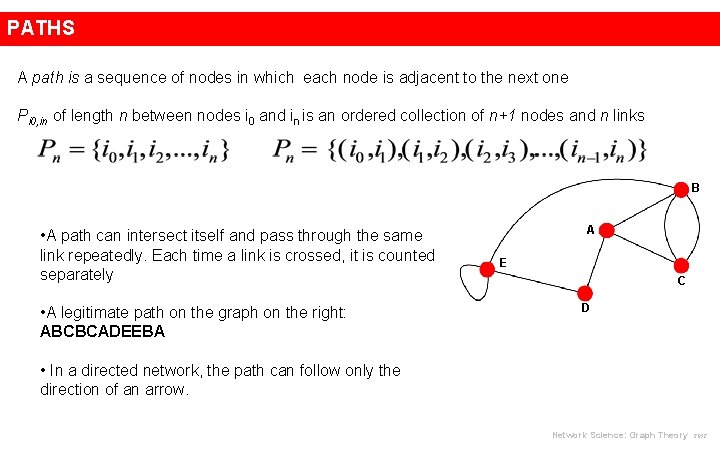
PATHS A path is a sequence of nodes in which each node is adjacent to the next one Pi 0, in of length n between nodes i 0 and in is an ordered collection of n+1 nodes and n links B • A path can intersect itself and pass through the same link repeatedly. Each time a link is crossed, it is counted separately • A legitimate path on the graph on the right: ABCBCADEEBA A E C D • In a directed network, the path can follow only the direction of an arrow. Network Science: Graph Theory 2012

PATHOLOGY: Cycle Path 1 1 2 5 3 4 A path with the same start and end node. A sequence of links/nodes. Network Science: Graph Theory 2012

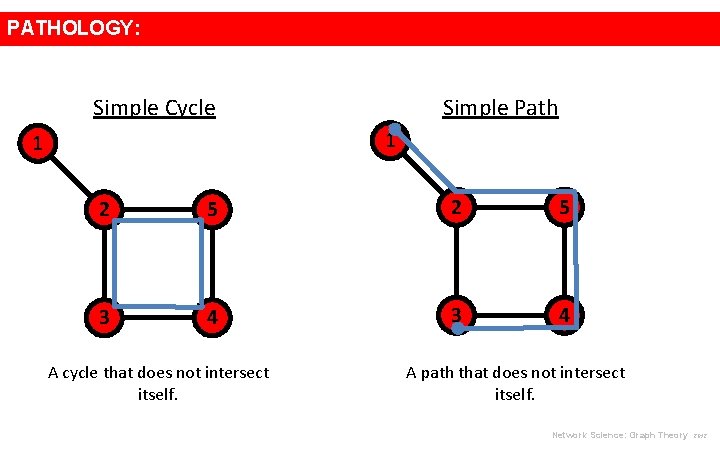
PATHOLOGY: Simple Cycle Simple Path 1 1 2 5 3 4 A cycle that does not intersect itself. A path that does not intersect itself. Network Science: Graph Theory 2012

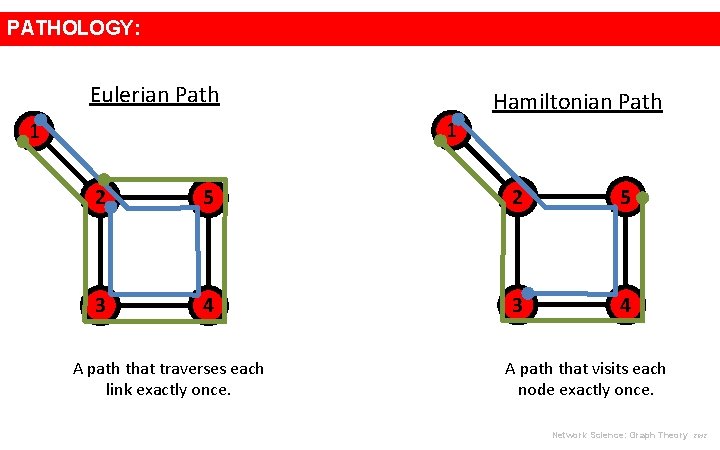
PATHOLOGY: Eulerian Path Hamiltonian Path 1 1 2 5 3 4 A path that traverses each link exactly once. A path that visits each node exactly once. Network Science: Graph Theory 2012

NUMBER OF PATHS BETWEEN TWO NODES Adjacency Matrix Nij, number of paths between any two nodes i and j: Length n=1: If there is a link between i and j, then Aij=1 and Aij=0 otherwise. Length n=2: If there is a path of length two between i and j, then Aik. Akj=1, and Aik. Akj=0 otherwise. The number of paths of length 2: Length n: In general, if there is a path of length n between i and j, then Aik…Alj=1 and Aik…Alj=0 otherwise. The number of paths of length n between i and j is* *holds for both directed and undirected networks. Network Science: Graph Theory 2012

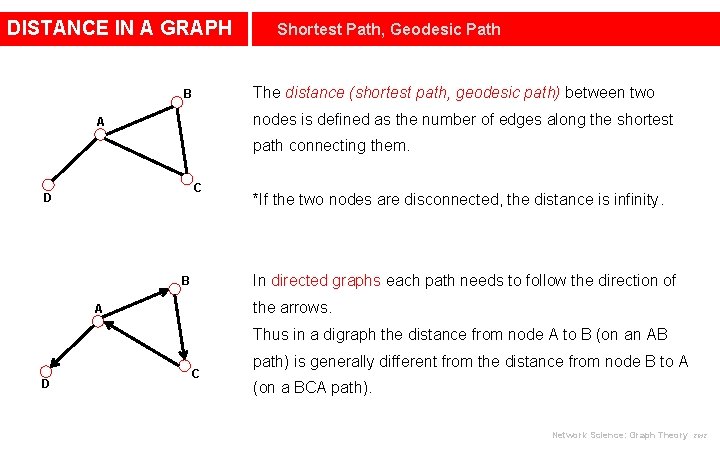
DISTANCE IN A GRAPH Shortest Path, Geodesic Path The distance (shortest path, geodesic path) between two B nodes is defined as the number of edges along the shortest A path connecting them. C D *If the two nodes are disconnected, the distance is infinity. In directed graphs each path needs to follow the direction of B the arrows. A Thus in a digraph the distance from node A to B (on an AB D C path) is generally different from the distance from node B to A (on a BCA path). Network Science: Graph Theory 2012

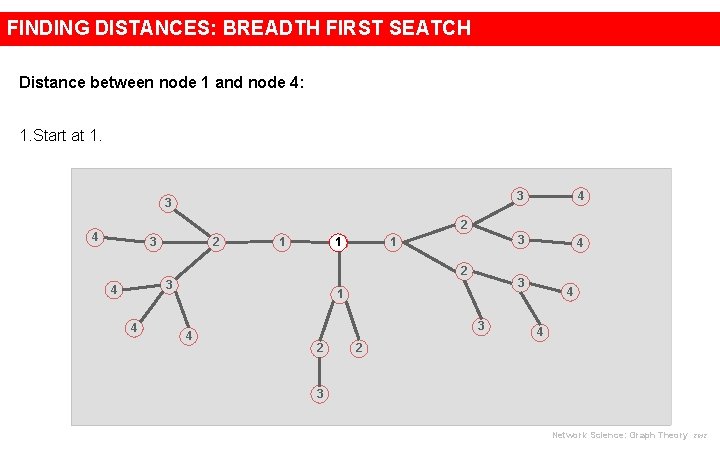
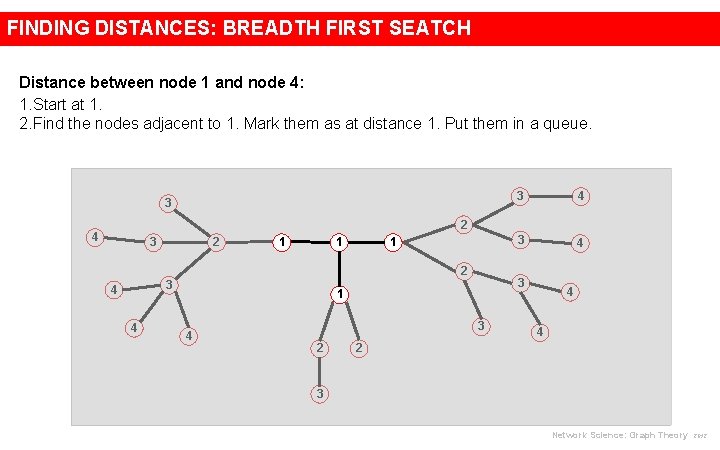
FINDING DISTANCES: BREADTH FIRST SEATCH Distance between node 1 and node 4: 1. Start at 1. 3 3 4 2 4 2 3 1 1 1 2 3 4 4 3 1 4 3 2 4 4 2 3 Network Science: Graph Theory 2012

FINDING DISTANCES: BREADTH FIRST SEATCH Distance between node 1 and node 4: 1. Start at 1. 2. Find the nodes adjacent to 1. Mark them as at distance 1. Put them in a queue. 3 3 4 2 4 2 3 1 1 1 2 3 4 4 3 1 4 3 2 4 4 2 3 Network Science: Graph Theory 2012

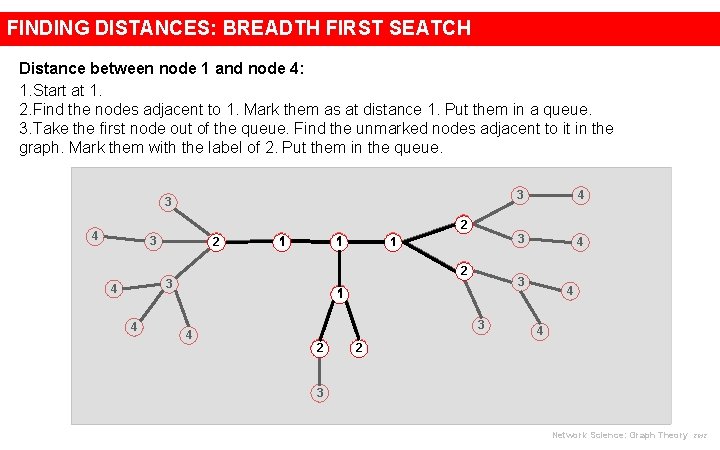
FINDING DISTANCES: BREADTH FIRST SEATCH Distance between node 1 and node 4: 1. Start at 1. 2. Find the nodes adjacent to 1. Mark them as at distance 1. Put them in a queue. 3. Take the first node out of the queue. Find the unmarked nodes adjacent to it in the graph. Mark them with the label of 2. Put them in the queue. 3 3 4 2 4 2 3 1 1 2 3 4 4 1 3 1 4 3 2 4 4 2 3 Network Science: Graph Theory 2012

FINDING DISTANCES: BREADTH FIRST SEATCH Distance between node 1 and node 4: 1. Repeat until you find node 4 or there are no more nodes in the queue. 2. The distance between 1 and 4 is the label of 4 or, if 4 does not have a label, infinity. 3 3 4 2 4 2 3 1 1 1 2 3 4 4 3 1 4 3 2 4 4 2 3 Network Science: Graph Theory 2012

NETWORK DIAMETER AND AVERAGE DISTANCE Diameter: dmax the maximum distance between any pair of nodes. What is the diameter of a disconnected graph? Average distance, <d>, for a connected directed graph: where dij is the distance from node i to node j Network Science: Graph Theory 2012

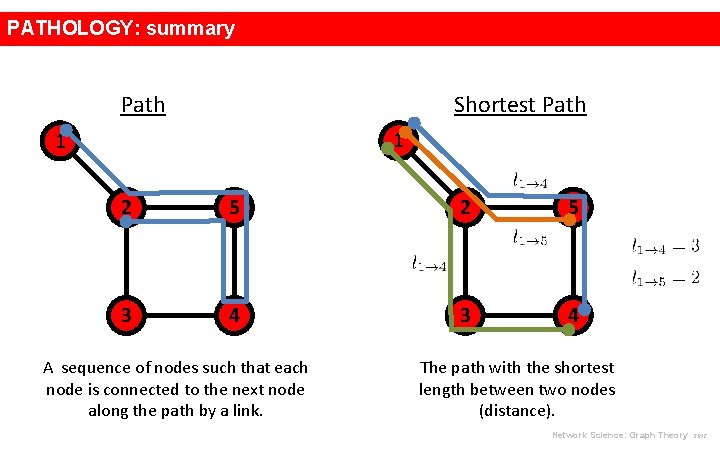
PATHOLOGY: summary Path Shortest Path 1 1 2 5 3 4 A sequence of nodes such that each node is connected to the next node along the path by a link. The path with the shortest length between two nodes (distance). Network Science: Graph Theory 2012

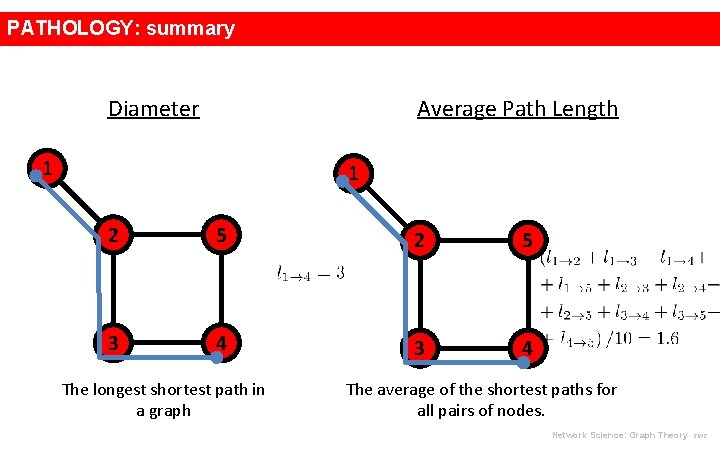
PATHOLOGY: summary Diameter Average Path Length 1 1 2 5 3 4 The longest shortest path in a graph The average of the shortest paths for all pairs of nodes. Network Science: Graph Theory 2012

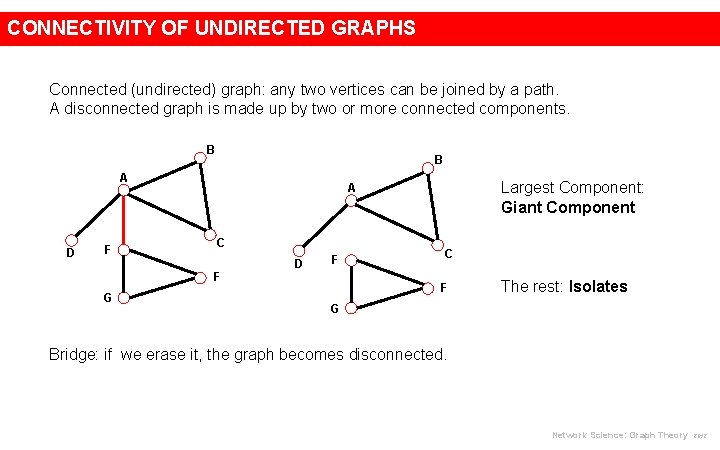
CONNECTIVITY OF UNDIRECTED GRAPHS Connected (undirected) graph: any two vertices can be joined by a path. A disconnected graph is made up by two or more connected components. B B A D F C D F F G Largest Component: Giant Component A C F The rest: Isolates G Bridge: if we erase it, the graph becomes disconnected. Network Science: Graph Theory 2012

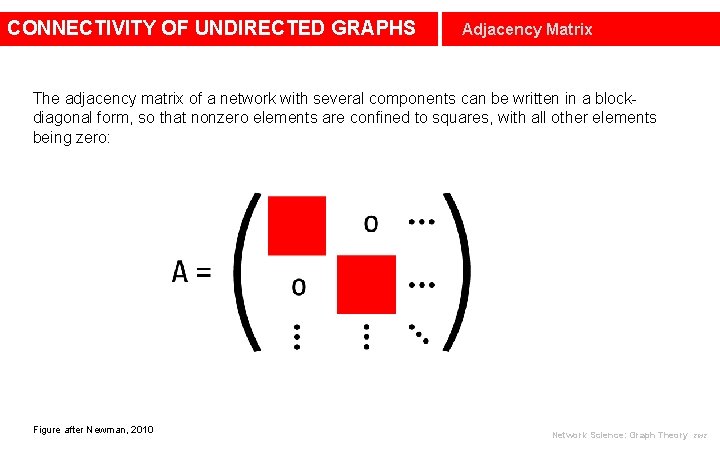
CONNECTIVITY OF UNDIRECTED GRAPHS Adjacency Matrix The adjacency matrix of a network with several components can be written in a blockdiagonal form, so that nonzero elements are confined to squares, with all other elements being zero: Figure after Newman, 2010 Network Science: Graph Theory 2012

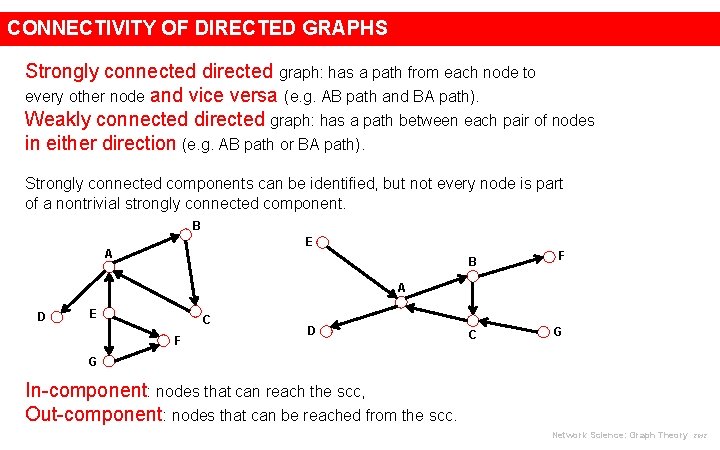
CONNECTIVITY OF DIRECTED GRAPHS Strongly connected directed graph: has a path from each node to every other node and vice versa (e. g. AB path and BA path). Weakly connected directed graph: has a path between each pair of nodes in either direction (e. g. AB path or BA path). Strongly connected components can be identified, but not every node is part of a nontrivial strongly connected component. B E A B F A D E C F D C G G In-component: nodes that can reach the scc, Out-component: nodes that can be reached from the scc. Network Science: Graph Theory 2012

THREE CENTRAL QUANTITIES IN NETWORK SCIENCE Degree distribution Average path length Clustering coefficient pk <d> C Network Science: Graph Theory 2012

Network Science: Graph Theory 2012

STATISTICS REMINDER We have a sample of values x 1, . . . , x. N Distribution of x (a. k. a. PDF): probability that a randomly chosen value is x P(x) = (# values x) / N Σi P(xi) = 1 always! Histograms >>> Network Science: Graph Theory 2012

DEGREE DISTRIBUTION Degree distribution P(k): probability that a randomly chosen vertex has degree k Nk = # nodes with degree k P(k) = Nk / N P(k) 0. 6 0. 5 0. 4 0. 3 0. 2 0. 1 1 2 3 4 k Network Science: Graph Theory 2012

CLUSTERING COEFFICIENT Local Clustering Coefficient: what portion of your neighbors are connected? Node i with degree ki Ci in [0, 1] Network Science: Graph Theory 2012

THREE CENTRAL QUANTITIES IN NETWORK SCIENCE Degree distribution: P(k) Path length: <d> Clustering coefficient: Network Science: Graph Theory 2012

THREE CENTRAL QUANTITIES IN NETWORK SCIENCE A. Degree distribution: B. Path length: C. Clustering coefficient: pk <d> Network Science: Graph Theory 2012

Network Science: Graph Theory 2012