Completing the Square and Solving Quadratics by Taking

Completing the Square and Solving Quadratics by Taking Square Roots

Perfect Square Trinomials • Some quadratics have special factoring rules which we have not yet discussed • These are in the form a 2 -2 ab+b 2 or a 2+2 ab+b 2 • They can be simplified to (a-b)2 and (a+b)2 • They can also be simplified using the box method to get the same result

Factor • x 2 -10 x+25 • Matches which form? a 2 -2 ab+b 2 or a 2+2 ab+b 2 • Simplified form (a-b)2 and (a+b)2

Factor • x 2+8 x+16

Factor • 40 x=8 x 2+50

Why bother discussing perfect square trinomials now? • They show up in solving square roots! • They show up when we complete the square!

Solving by taking square roots • To solve a quadratic equation you can take the square root of both sides • First simplify so the squared term is on one side of the equal sign and everything else is on the other! • The key is to remember the positive and negative square roots

Solve 3 x 2 -4

Solve 4 x 2 -20=5
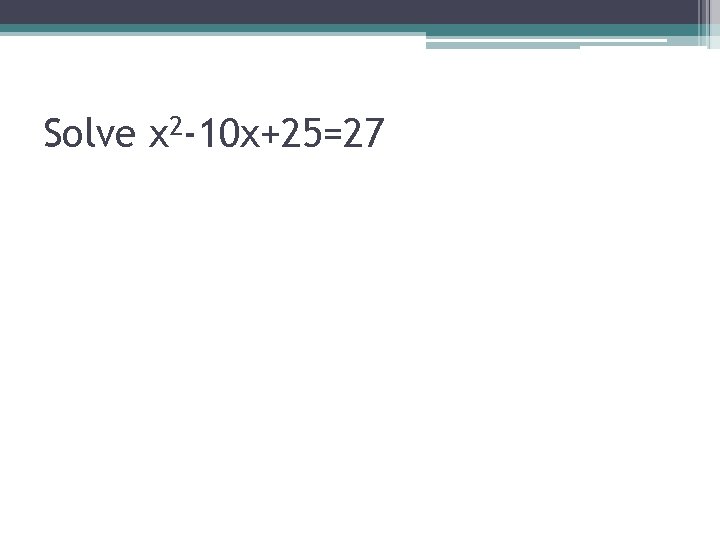
Solve x 2 -10 x+25=27

Solve x 2+8 x+16=49

Completing the Square • Solving with the method above, can be used only when the expressions work out to be nice squares • When you are presented with a problem not modeled in the form x 2+bx, you can add a term to form a perfect square trinomial • Called completing the square

Completing the Square •


Steps in Completing the Square • 1. Collect variable terms on one side of the equation and constants on the other • 2. As needed, divide both sides by “a” to make the coefficient of the x 2 term 2 • 3. Complete the square by adding (b/2)2 to EACH side of the equation • 4. Factor the variable as a perfect square trinomial • 5. Take square root of both sides of the equation and solve for the values of the variable including + and -

Solve X 2=27 -6 x • 1. Get all variables to one side • 2. Setup to complete the square • 3. Add (b/2)2 to each side

• 4. Perfect square trinomial form • 5. Solve

Solve 2 x 2+8 x=12 • 1. Get all variables to one side • 2. Setup to complete the square • 3. Add (b/2)2 to each side

• 4. Perfect square trinomial form • 5. Solve

Solve x 2 -6 x=-4 • 1. Get all variables to one side • 2. Setup to complete the square • 3. Add (b/2)2 to each side

Try in your groups • 3 x 2 -24 x=27

• 4. Perfect square trinomial form • 5. Solve
- Slides: 22