Compiler Design CSE 504 Type Checking Department of

Compiler Design – CSE 504 Type Checking Department of Computer Science, Stony Brook University 1

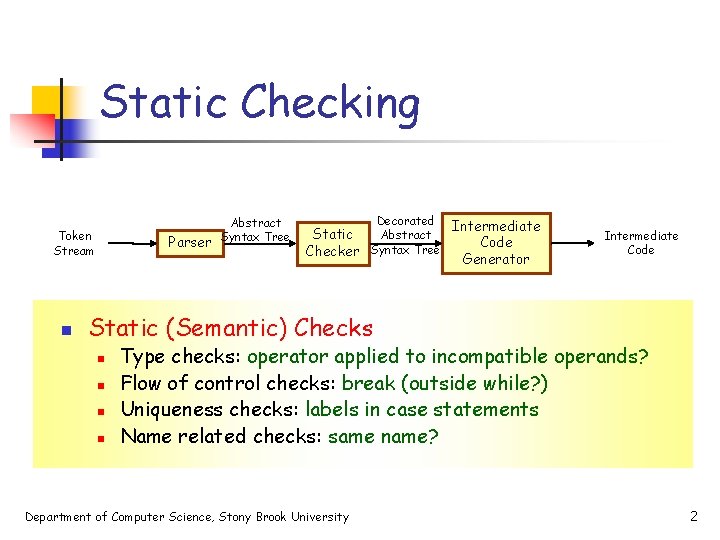
Static Checking Token Stream n Parser Abstract Syntax Tree Decorated Static Abstract Checker Syntax Tree Intermediate Code Generator Intermediate Code Static (Semantic) Checks n n Type checks: operator applied to incompatible operands? Flow of control checks: break (outside while? ) Uniqueness checks: labels in case statements Name related checks: same name? Department of Computer Science, Stony Brook University 2

Type Checking n n n Problem: Verify that a type of a construct matches that expected by its context. Examples: n mod requires integer operands (PASCAL) n * (dereferencing) – applied to a pointer n a[i] – indexing applied to an array n f(a 1, a 2, …, an) – function applied to correct arguments. Information gathered by a type checker: n Needed during code generation. Department of Computer Science, Stony Brook University 3

Type Systems n A collection of rules for assigning type expressions to the various parts of a program. n Based on: Syntactic constructs, notion of a type. n Example: If both operators of “+”, “-”, “*” are of type integer then so is the result. n Type Checker: An implementation of a type system. n n Syntax Directed. Sound Type System: eliminates the need for checking type errors during run time. Department of Computer Science, Stony Brook University 4

Type Expressions n Implicit Assumptions: n n Each program has a type Types have a structure Basic Types Statements Type Constructors Boolean Character Arrays Real Integer Records Enumerations Sub-ranges Sets Void Error Pointers Variables Names Functions Department of Computer Science, Stony Brook University Expressions 5

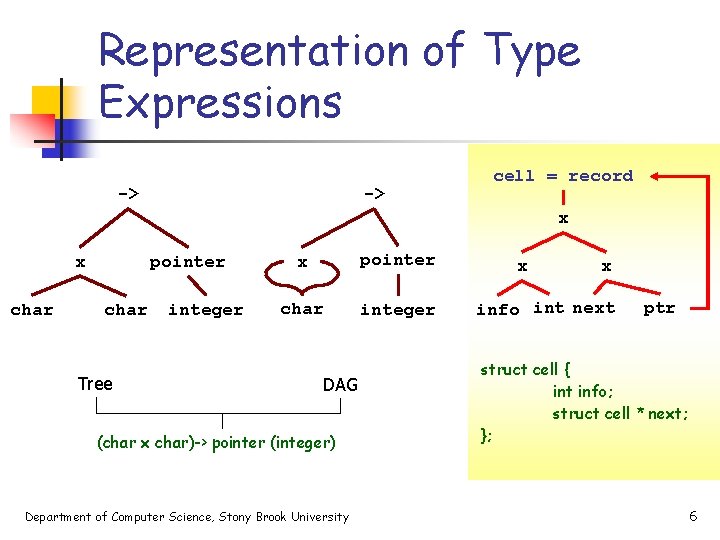
Representation of Type Expressions -> -> cell = record x x char pointer char Tree integer x pointer char integer DAG (char x char)-> pointer (integer) Department of Computer Science, Stony Brook University x x info int next ptr struct cell { int info; struct cell * next; }; 6

Type Expressions Grammar Type -> int | float | char | … | void | error | name | variable | array( size, Type) | record( (name, Type)*) | pointer( Type) | tuple((Type)*) | arrow(Type, Type) Department of Computer Science, Stony Brook University Basic Types Structured Types 7

A Simple Typed Language Program -> Declaration; Statement Declaration -> Declaration; Declaration | id: Type Statement -> Statement; Statement | id : = Expression | if Expression then Statement | while Expression do Statement Expression -> literal | num | id | Expression mod Expression | E[E] | E ↑ | E (E) Department of Computer Science, Stony Brook University 8

Type Checking Expressions E -> int_const { E. type = int } E -> float_const { E. type = float } E -> id { E. type = sym_lookup(id. entry, type) } E -> E 1 + E 2 {E. type = if E 1. type {int, float} | E 2. type {int, float} then error else if E 1. type == E 2. type == int then int else float } Department of Computer Science, Stony Brook University 9

Type Checking Expressions E -> E 1 [E 2] {E. type = if E 1. type = array(S, T) & E 2. type = int then T else error} E -> *E 1 E -> &E 1 E -> E 1 (E 2) E -> (E 1, E 2) {E. type = if E 1. type = pointer(T) then T else error} {E. type = pointer(E 1. tye)} {E. type = if (E 1. type = arrow(S, T) & E 2. type = S, then T else err} {E. type = tuple(E 1. type, E 2. type)} Department of Computer Science, Stony Brook University 10

Type Checking Statements S -> id : = E S -> if E then S 1 S -> while E do S 1 S -> S 1; S 2 Department of Computer Science, Stony Brook University {S. type : = if id. type = E. type then void else error} {S. type : = if E. type = boolean then S 1. type} {S. type : = if S 1. type = void ∧ S 2. type = void then void else error} 11

Equivalence of Type Expressions Problem: When in E 1. type = E 2. type? n n We need a precise definition for type equivalence Interaction between type equivalence and type representation Example: type vector = array [1. . 10] of real type weight = array [1. . 10] of real var x, y: vector; z: weight Name Equivalence: When they have the same name. n x, y have the same type; z has a different type. Structural Equivalence: When they have the same structure. n x, y, z have the same type. Department of Computer Science, Stony Brook University 12

Structural Equivalence n Definition: by Induction n n (basis) (induction step) In Practice: modifications are needed n n n Same basic type Same constructor applied to SE Type Same DAG Representation Do not include array bounds – when they are passed as parameters Other applied representations (More compact) Can be applied to: Tree/ DAG n n Does not check for cycles Later improve it. Department of Computer Science, Stony Brook University 13

Algorithm Testing Structural Equivalence function stequiv(s, t): boolean { if (s & t are of the same basic type) return true; if (s = array(s 1, s 2) & t = array(t 1, t 2)) return equal(s 1, t 1) & stequiv(s 2, t 2); if (s = tuple(s 1, s 2) & t = tuple(t 1, t 2)) return stequiv(s 1, t 1) & stequiv(s 2, t 2); if (s = arrow(s 1, s 2) & t = arrow(t 1, t 2)) return stequiv(s 1, t 1) & stequiv(s 2, t 2); } if (s = pointer(s 1) & t = pointer(t 1)) return stequiv(s 1, t 1); Department of Computer Science, Stony Brook University 14

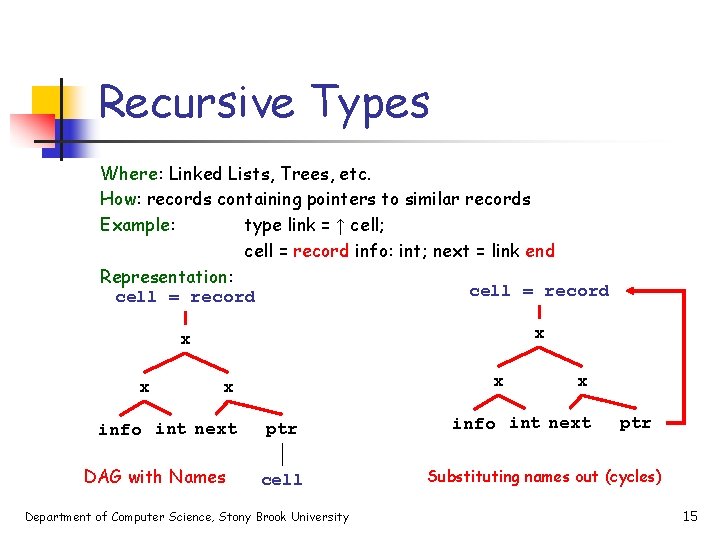
Recursive Types Where: Linked Lists, Trees, etc. How: records containing pointers to similar records Example: type link = ↑ cell; cell = record info: int; next = link end Representation: cell = record x x x info int next DAG with Names ptr cell Department of Computer Science, Stony Brook University x info int next ptr Substituting names out (cycles) 15

Recursive Types in C Policy: avoid cycles in type graphs by: n n n Example: n n Using structural equivalence for all types Except for records -> name equivalence struct cell {int info; struct cell * next; } Name use: name cell becomes part of the type of the record. n n Use the acyclic representation Names declared before use – except for pointers to records. Cycles – potential due to pointers in records Testing for structural equivalence stops when a record constructor is reached ~ same named record type? Department of Computer Science, Stony Brook University 16

Overloading Functions & Operators n Overloaded Symbol: one that has different meanings depending on its context n Example: Addition operator + n Resolving (operator identification): overloading is resolved when a unique meaning is determined. n Context: it is not always possible to resolve overloading by looking only the arguments of a function n n Set of possible types Context (inherited attribute) necessary Department of Computer Science, Stony Brook University 17

Overloading Example function “*” (i, j: integer) return complex; function “*” (x, y: complex) return complex; * Has the following types: arrow(tuple(integer, integer), complex) arrow(tuple(complex, complex) int i, j; k = i * j; Department of Computer Science, Stony Brook University 18

Narrowing Down Types E’ -> E E -> id E -> E 1(E 2) {E’. types = E. types E. unique = if E’. types = {t} then t else error} {E. types = lookup(id. entry)} {E. types = {s’ | s E 2. types and S->s’ E 1. types} t = E. unique S = {s | s E 2. types and S->t E 1. types} E 2. unique = if S ={s} the S else error E 1. unique = if S = {s} the S->t else error Department of Computer Science, Stony Brook University 19

Polymorphic Functions n Defn: a piece of code (functions, operators) that can be executed with arguments of different types. n Examples: Built in Operator indexing arrays, pointer manipulation n Why use them: facilitate manipulation of data structures regardless of types. n Example HL: fun length(lptr) = if null (lptr) then 0 else length(+l(lptr)) + 1 Department of Computer Science, Stony Brook University 20

A Language for Polymorphic Functions P -> D ; E D -> D ; D | id : Q Q -> α. Q | T T -> arrow (T, T) | tuple (T, T) | unary (T) | basic |α E -> E (E) | E, E | id Department of Computer Science, Stony Brook University 21

Type Variables n Why: variables representing type expressions allow us to talk about unknown types. n n Application: check consistent usage of identifiers in a language that does not require identifiers to be declared before usage. n n Use Greek alphabets α, β, γ … A type variable represents the type of an undeclared identifier. Type Inference Problem: Determine the type of a language constant from the way it is used. n We have to deal with expressions containing variables. Department of Computer Science, Stony Brook University 22

Examples of Type Inference Type link ↑ cell; Procedure mlist (lptr: link; procedure p); { while lptr <> null { p(lptr); lptr : = lptr ↑. next} } Hence: p: link -> void Function deref (p) { return p ↑; } P: β, β = pointer(α) Hence deref: α. pointer(α) -> α Department of Computer Science, Stony Brook University 23

Program in Polymorphic Language deref: α. pointer(α) -> α q: pointer (integer)) deref (deref( (q)) apply: α 0 deref 0: pointer (α 0 ) -> α 0 Notation: -> arrow x tuple apply: αi deref 0: pointer (αi ) -> αi q: pointer (integer)) Subsripts i and o distinguish between the inner and outer occurrences of deref, respectively. Department of Computer Science, Stony Brook University 24

Type Checking Polymorphic Functions n Distinct occurrences of a p. f. in the same expression need not have arguments of the same type. n n n The notion of type equivalence changes in the presence of variables. n n deref (q)) Replace α with fresh variable and remove (αi, αo) Use unification: check if s and t can be made structurally equivalent by replacing type vars by the type expression. We need a mechanism for recording the effect of unifying two expressions. n A type variable may occur in several type expressions. Department of Computer Science, Stony Brook University 25

Substitutions and Unification Substitution: a mapping from type variables to type expressions. Function subst (t: type Expr): type Expr { S if (t is a basic type) return t; if (t is a basic variable) return S(t); --identify if t S if (t is t 1 -> t 2) return subst(t 1) -> subst (t 2); } n n Instance: S(t) is an instance of t written S(t) < t. n Examples: pointer (integer) < pointer (α) , int -> real ≠ α-> α n Unify: t 1 ≈ t 2 if S. S (t 1) = S (t 2) n Most General Unifier S: A substitution S: n n S (t 1) = S (t 2) S’. S’ (t 1) = S’ (t 2) t. S’(t) < S(t). Department of Computer Science, Stony Brook University 26

Polymorphic Type checking Translation Scheme E -> E 1 (E 2) E -> E 1, E 2 E -> id { p : = mkleaf(newtypevar); unify (E 1. type, mknode(‘->’, E 2. type, p); E. type = p} {E. type : = mknode(‘x’, E 1. type, E 2. type); } { E. type : = fresh (id. type) } fresh (t): replaces bound vars in t by fresh vars. Returns pointer to a node representing result. type. fresh( α. pointer(α) -> α) = pointer(α 1) -> α 1. unify (m, n): unifies expressions represented by m and n. n n Side-effect: keep track of substitution Fail-to-unify: abort type checking. Department of Computer Science, Stony Brook University 27

PType Checking Example Given: derefo (derefi (q)) q = pointer (int)) -> : 3 Bottom Up: fresh ( α. Pointer(α) -> α) derefo derefi pointer : 2 q -> : 3 -> : 6 pointer : 9 pointer : 2 pointer : 5 pointer : 8 αo : 1 αi : 4 -> : 3 m-> : 6 pointer : 2 pointer : 5 αo : 1 αi : 4 α: 1 integer : 7 Department of Computer Science, Stony Brook University n-> : 6 pointer : 5 β : 8 pointer : 8 integer : 7 28