COMPILER DESIGN BCA 5 th Semester 2020 Topic

COMPILER DESIGN BCA 5 th Semester 2020 Topic: Code Optimization Sakhi Bandyopadhyay Department of Computer Science and BCA Kharagpur College

Introduction Criteria for Code-Improving Transformation: • Meaning must be preserved (correctness) • Speedup must occur on average. • Work done must be worth the effort. Opportunities: • Programmer (algorithm, directives) • Intermediate code • Target code

Peephole Optimizations 1. A Simple but effective technique for locally improving the target code is peephole optimization, 2. a method for trying to improve the performance of the target program 3. by examining a short sequence of target instructions and replacing these instructions by a shorter or faster sequence whenever possible. Characteristics of peephole optimization 1. Redundant instruction elimination 2. Flow of control information 3. Algebraic Simplification 4. Use of machine Idioms

Peephole Optimizations Constant Folding x : = 32 x : = x + 32 becomes x : = 64 Unreachable Code goto L 2 x : = x + 1 No need Flow of control optimizations goto L 1 becomes goto L 2 … L 1: goto L 2 No needed if no other L 1 branch

Peephole Optimizations Algebraic Simplification x : = x + 0 No needed Dead code x : = 32 where x not used after statement y : = x + y y : = y + 32 Reduction in strength x : = x * 2 x : = x + x x : = x << 2

Basic Blocks and Flow Graphs A graph representation of three address statements, called flow graph. Nodes in the flow graph represent computations Edges represent the flow of control Basic Block: A basic block is a sequence of consecutive statements in which flow of control enters at the beginning and leaves at the end without halt or possibly of the branching except at the end.

Basic Blocks and Flow Graphs (2) This is a basic block t 1 = a*a t 2 = a*b t 3 = 2*t 2 t 4 = t 1+t 3 t 5 = b*b t 6 = t 4+ t 5 Three address statement x = y + z is said to define x and to use y and z. A name in a basic block is said to be live at a given point if its value is used after that point in the program, perhaps in another basic block

Basic Blocks and Flow Graphs (3) Partition into basic blocks – Method • We first determine the leader – The first statement is a leader – Any statement that is the target of a conditional or unconditional goto is a leader – Any statement that immediately follows a goto or unconditional goto statement is a leader • For each leader, its basic block consists of the leader and all the statements up to but not including the next leader or the end of the program.

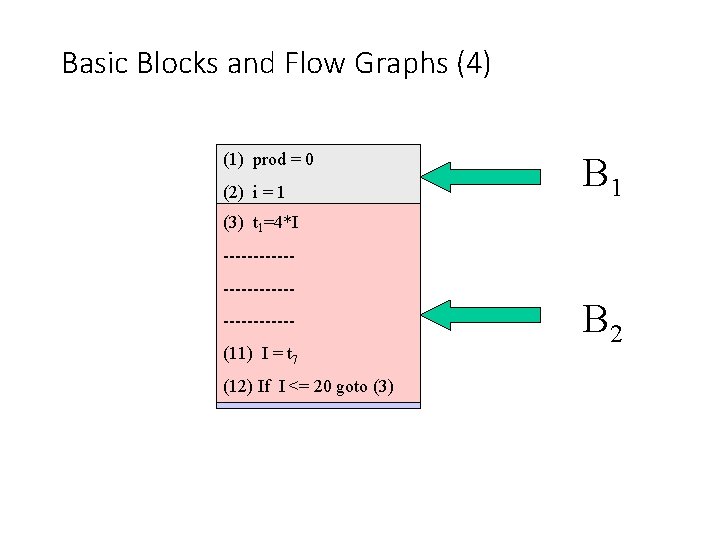
Basic Blocks and Flow Graphs (4) (1) prod = 0 (2) i = 1 B 1 (3) t 11=4*I -----------------(11) I = t 77 (12) If I <= 20 goto (3) B 2

Transformation on Basic Block A basic block computes a set of expressions. Transformations are useful for improving the quality of code. Two important classes of local optimizations that can be applied to a basic blocks – Structure Preserving Transformations – Algebraic Transformations

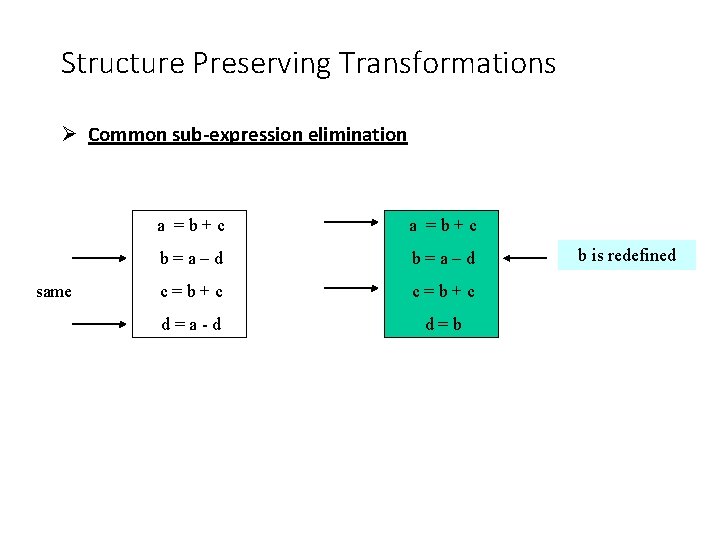
Structure Preserving Transformations Common sub-expression elimination same a =b+c b=a–d c=b+c d=a-d d=b b is redefined

Structure Preserving Transformations Dead – Code Elemination Say, x is dead, that is never subsequently used, at the point where the statement x = y + z appears in a block. We can safely remove x Renaming Temporary Variables – say, t = b+c where t is a temporary var. – If we change u = b+c, then change all instances of t to u. Interchange of Statements – t 1 = b + c – t 2 = x + y – We can interchange iff neither x nor y is t 1 and neither b nor c is t 2

Algebraic Transformations Replace expensive expressions by cheaper one – X=X+0 eliminate – X=X*1 eliminate – X = y**2 (why expensive? Answer: Normally implemented by function call) • by X = y * y Flow graph: – We can add flow of control information to the set of basic blocks making up a program by constructing directed graph called flow graph. – There is a directed edge from block B 1 to block B 2 if • There is conditional or unconditional jump from the last statement of B 1 to the first statement of B 2 or • B 2 is immediately follows B 1 in the order of the program, and B 1 does not end in an unconditional jump.

Loops A loop is a collection of nodes in a flow graph such that – All nodes in the collection are strongly connected, that is from any node in the loop to any other, there is a path of length one or more, wholly within the loop, and – The collection of nodes has a unique entry, that is, a node in the loop such that, the only way to reach a node from a node out side the loop is to first go through the entry.

1 A = 4*i 2 B = a[A] 3 C = 4*i 4 D = b[C] 5 E=B*D 6 F = prod + E 7 Prod = F 8 G=i+1 9 i=G 10 if I <= 20 goto (1) The DAG representation of Basic Block + * prod <= [] [] a b 4 20 + * i 0 1

Exercise given the code fragment x : = a*a + 2*a*b + b*b; y : = a*a – 2*a*b + b*b; draw the dependency graph before and after common subexpression elimination.

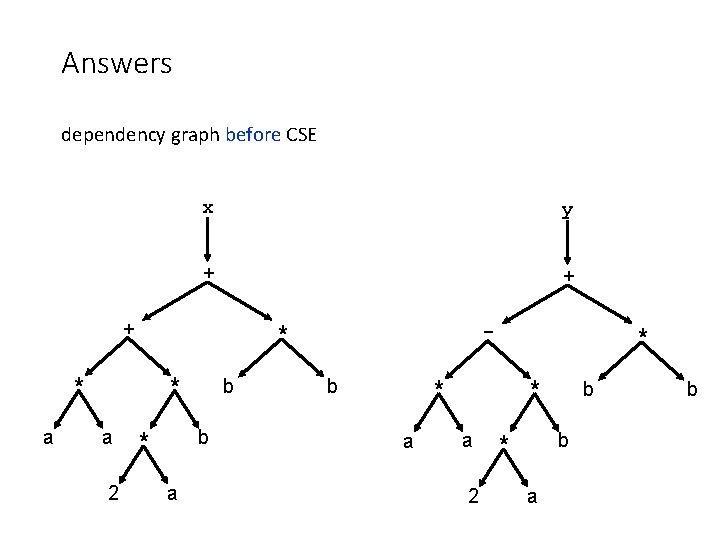
Answers dependency graph before CSE x y + + + * a 2 - * b b * a b * * a 2 b b * a b

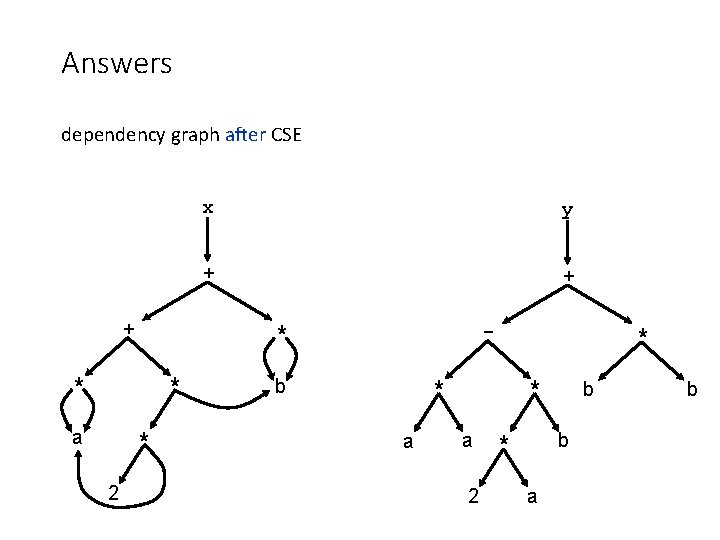
Answers dependency graph after CSE + * * 2 y + + - * * a x b * * a 2 b b * a b

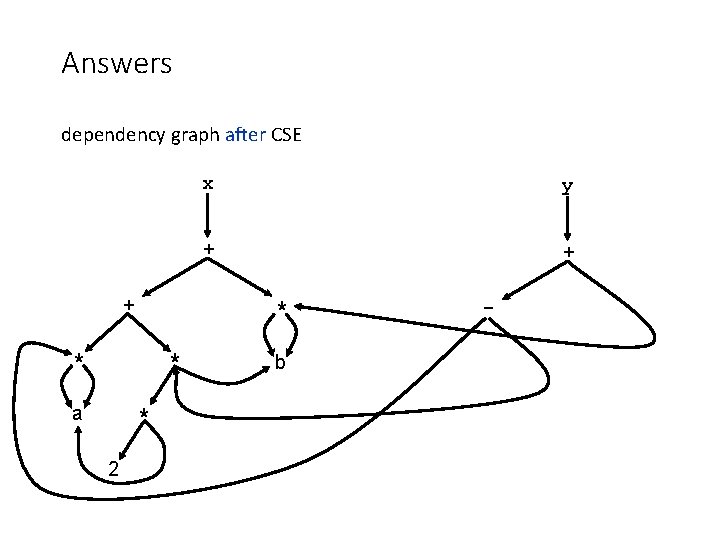
Answers dependency graph after CSE + * * 2 y + + * * a x b -

Basic Block Level 1. 2. 3. 4. 5. Common Sub expression elimination Constant Propagation Copy Propagation Dead code elimination …

Common expression can be eliminated Simple example: a[i+1] = b[i+1] t 1 = i+1 t 2 = b[t 1] t 3 = i + 1 a[t 3] = t 2 t 1 = i + 1 t 2 = b[t 1] t 3 = i + 1 no longer live a[t 1] = t 2

Now, suppose i is a constant: i=4 t 1 = i+1 t 2 = b[t 1] a[t 1] = t 2 Final Code: i=4 t 1 = 5 t 2 = b[t 1] a[t 1] = t 2 i=4 t 2 = b[5] a[5] = t 2 i=4 t 1 = 5 t 2 = b[5] a[5] = t 2

Optimizations on CFG Must take control flow into account • • • Common Sub-expression Elimination Constant Propagation Dead Code Elimination Partial redundancy Elimination … Applying one optimization may raise opportunities for other optimizations.

Simple Loop Optimizations Code Motion Move invariants out of the loop. Example: while (i <= limit - 2) becomes t : = limit - 2 while (i <= t)

Three Address Code of Quick Sort 1 i=m-1 16 t 7 = 4 * I 2 j=n 17 t 8 = 4 * j 3 t 1 =4 * n 18 4 v = a[t 1] 19 t 9 = a[t 8] 5 i=i +1 20 6 t 2 = 4 * i 21 7 8 9 10 11 t 3 = a[t 2] if t 3 < v goto (5) j=j– 1 t 4 = 4 * j 22 23 a[t 7] = t 9 t 10 = 4 * j a[t 10] = x goto (5) 24 t 11 = 4 * I 25 x = a[t 11] 26 t 12 = 4 * i 27 t 13 = 4 * n 12 t 5 = a[t 4] 13 if t 5 > v goto (9) 28 14 if i >= j goto (23) t 14 = a[t 13] 29 15 t 6 = 4 * i a[t 12] = t 14 30 t 15 = 4 * n x = a[t 6] a[t ] = x

Find The Basic Block 1 i=m-1 16 t 7 = 4 * I 2 j=n 17 t 8 = 4 * j 3 t 1 =4 * n 18 4 v = a[t 1] 19 t 9 = a[t 8] 5 i=i +1 20 6 t 2 = 4 * i 21 7 8 9 10 11 t 3 = a[t 2] if t 3 < v goto (5) j=j– 1 t 4 = 4 * j 22 23 a[t 7] = t 9 t 10 = 4 * j a[t 10] = x goto (5) 24 t 11 = 4 * i 25 x = a[t 11] 26 t 12 = 4 * i 27 t 13 = 4 * n 12 t 5 = a[t 4] 13 if t 5 > v goto (9) 28 14 if i >= j goto (23) t 14 = a[t 13] 29 15 t 6 = 4 * i a[t 12] = t 14 30 t 15 = 4 * n x = a[t 6] a[t ] = x

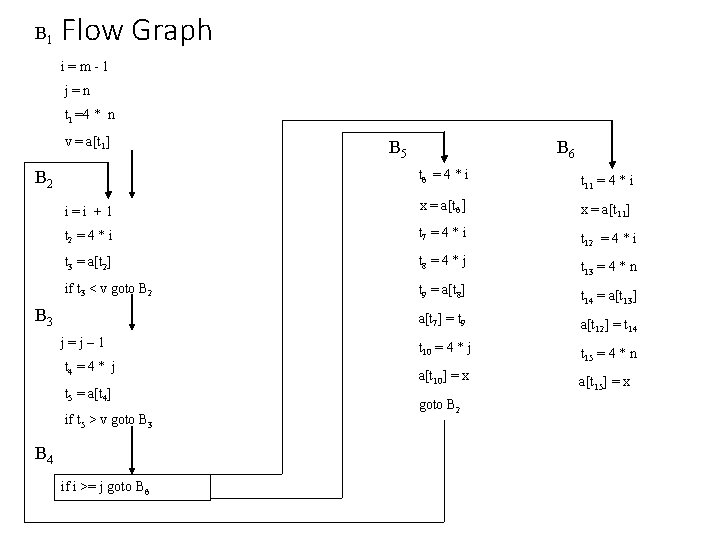
B 1 Flow Graph i=m-1 j=n t 1 =4 * n v = a[t 1] B 5 B 6 t 6 = 4 * i t 11 = 4 * i i=i +1 x = a[t 6] x = a[t 11] t 2 = 4 * i t 7 = 4 * i t 12 = 4 * i t 3 = a[t 2] t 8 = 4 * j t 13 = 4 * n if t 3 < v goto B 2 t 9 = a[t 8] t 14 = a[t 13] a[t 7] = t 9 a[t 12] = t 14 t 10 = 4 * j t 15 = 4 * n a[t 10] = x a[t 15] = x B 2 B 3 j=j– 1 t 4 = 4 * j t 5 = a[t 4] if t 5 > v goto B 3 B 4 if i >= j goto B 6 goto B 2

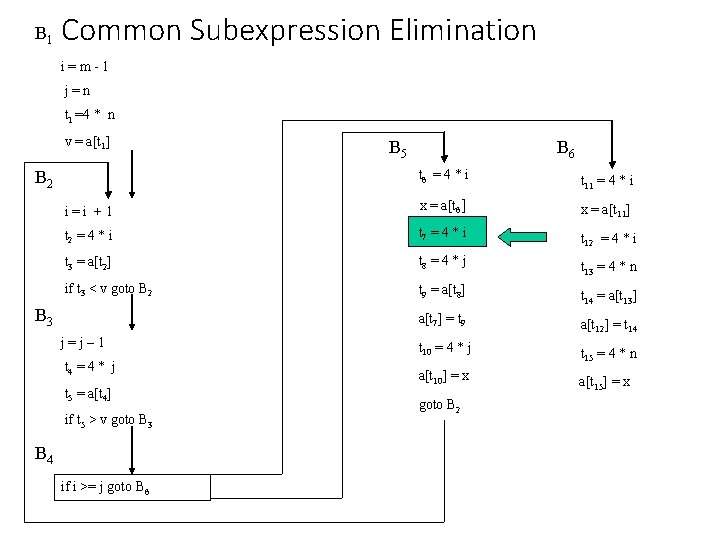
B 1 Common Subexpression Elimination i=m-1 j=n t 1 =4 * n v = a[t 1] B 5 B 6 t 6 = 4 * i t 11 = 4 * i i=i +1 x = a[t 6] x = a[t 11] t 2 = 4 * i t 7 = 4 * i t 12 = 4 * i t 3 = a[t 2] t 8 = 4 * j t 13 = 4 * n if t 3 < v goto B 2 t 9 = a[t 8] t 14 = a[t 13] a[t 7] = t 9 a[t 12] = t 14 t 10 = 4 * j t 15 = 4 * n a[t 10] = x a[t 15] = x B 2 B 3 j=j– 1 t 4 = 4 * j t 5 = a[t 4] if t 5 > v goto B 3 B 4 if i >= j goto B 6 goto B 2

B 1 Common Subexpression Elimination i=m-1 j=n t 1 =4 * n v = a[t 1] B 5 B 6 t 6 = 4 * i t 11 = 4 * i i=i +1 x = a[t 6] x = a[t 11] t 2 = 4 * i t 8 = 4 * j t 12 = 4 * i t 3 = a[t 2] t 9 = a[t 8] t 13 = 4 * n if t 3 < v goto B 2 a[t 6] = t 9 t 14 = a[t 13] t 10 = 4 * j a[t 12] = t 14 a[t 10] = x t 15 = 4 * n goto B 2 a[t 15] = x B 2 B 3 j=j– 1 t 4 = 4 * j t 5 = a[t 4] if t 5 > v goto B 3 B 4 if i >= j goto B 6

B 1 Common Subexpression Elimination i=m-1 j=n t 1 =4 * n v = a[t 1] B 5 B 6 t 6 = 4 * i t 11 = 4 *i i=i +1 x = a[t 6] x = a[t 11] t 2 = 4 * i t 8 = 4 * j t 12 = 4 * i t 3 = a[t 2] t 9 = a[t 8] t 13 = 4 * n if t 3 < v goto B 2 a[t 6] = t 9 t 14 = a[t 13] a[t 8] = x a[t 12] = t 14 goto B 2 t 15 = 4 * n B 2 B 3 j=j– 1 t 4 = 4 * j t 5 = a[t 4] if t 5 > v goto B 3 B 4 if i >= j goto B 6 a[t 15] = x

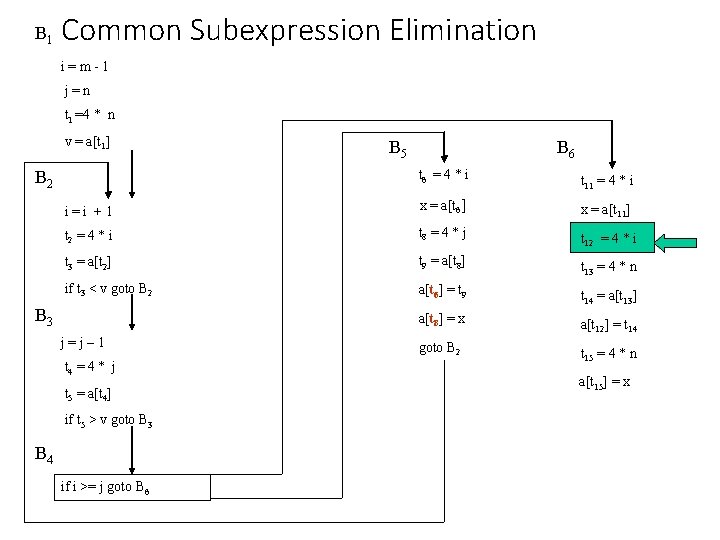
B 1 Common Subexpression Elimination i=m-1 j=n t 1 =4 * n v = a[t 1] B 5 B 6 t 6 = 4 * i t 11 = 4 * i i=i +1 x = a[t 6] x = a[t 11] t 2 = 4 * i t 8 = 4 * j t 12 = 4 * i t 3 = a[t 2] t 9 = a[t 8] t 13 = 4 * n if t 3 < v goto B 2 a[t 6] = t 9 t 14 = a[t 13] a[t 8] = x a[t 12] = t 14 goto B 2 t 15 = 4 * n B 2 B 3 j=j– 1 t 4 = 4 * j t 5 = a[t 4] if t 5 > v goto B 3 B 4 if i >= j goto B 6 a[t 15] = x

B 1 Common Subexpression Elimination i=m-1 j=n t 1 =4 * n v = a[t 1] B 5 B 6 t 6 = 4 * i t 11 = 4 * i i=i +1 x = a[t 6] x = a[t 11] t 2 = 4 * i t 8 = 4 * j t 13 = 4 * n t 3 = a[t 2] t 9 = a[t 8] t 14 = a[t 13] if t 3 < v goto B 2 a[t 6] = t 9 a[t 11] = t 14 a[t 8] = x t 15 = 4 * n goto B 2 a[t 15] = x B 2 B 3 j=j– 1 t 4 = 4 * j t 5 = a[t 4] if t 5 > v goto B 3 B 4 if i >= j goto B 6

B 1 Common Subexpression Elimination i=m-1 j=n t 1 =4 * n v = a[t 1] B 5 B 6 t 6 = 4 * i B 2 i=i +1 x = a[t 6] t 2 = 4 * i t 8 = 4 * j t 3 = a[t 2] t 9 = a[t 8] if t 3 < v goto B 2 a[t 6] = t 9 B 3 a[t 8] = x j=j– 1 t 4 = 4 * j t 5 = a[t 4] if t 5 > v goto B 3 B 4 if i >= j goto B 6 goto B 2 t 11 = 4 * i x = a[t 11] t 13 = 4 * n t 14 = a[t 13] a[t 11] = t 14 a[t 13] = x

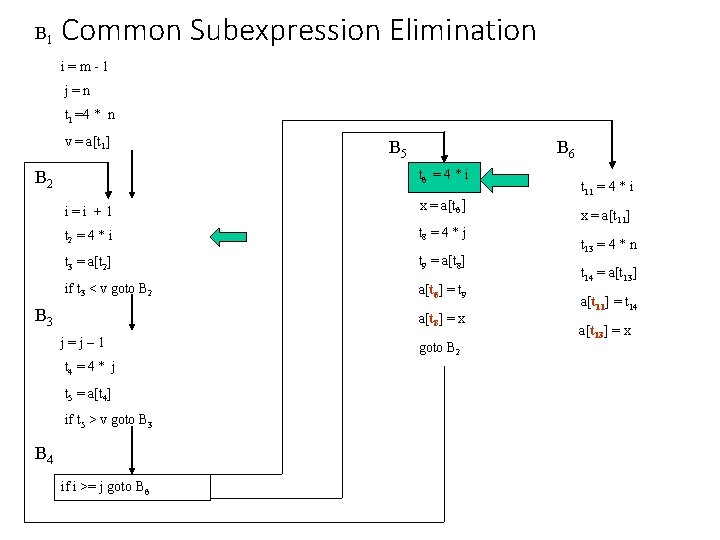
B 1 Common Subexpression Elimination i=m-1 j=n t 1 =4 * n v = a[t 1] B 5 B 6 t 6 = 4 * i B 2 i=i +1 x = a[t 6] t 2 = 4 * i t 8 = 4 * j t 3 = a[t 2] t 9 = a[t 8] if t 3 < v goto B 2 a[t 6] = t 9 B 3 a[t 8] = x j=j– 1 t 4 = 4 * j t 5 = a[t 4] if t 5 > v goto B 3 B 4 if i >= j goto B 6 goto B 2 t 11 = 4 * i x = a[t 11] t 13 = 4 * n t 14 = a[t 13] a[t 11] = t 14 a[t 13] = x

B 1 Common Subexpression Elimination i=m-1 j=n t 1 =4 * n v = a[t 1] B 5 B 6 x = a[t 2] B 2 i=i +1 t 8 = 4 * j t 2 = 4 * i t 9 = a[t 8] t 3 = a[t 2] = t 9 if t 3 < v goto B 2 a[t 8] = x B 3 goto B 2 j=j– 1 t 4 = 4 * j t 5 = a[t 4] if t 5 > v goto B 3 B 4 if i >= j goto B 6 t 11 = 4 * i x = a[t 11] t 13 = 4 * n t 14 = a[t 13] a[t 11] = t 14 a[t 13] = x

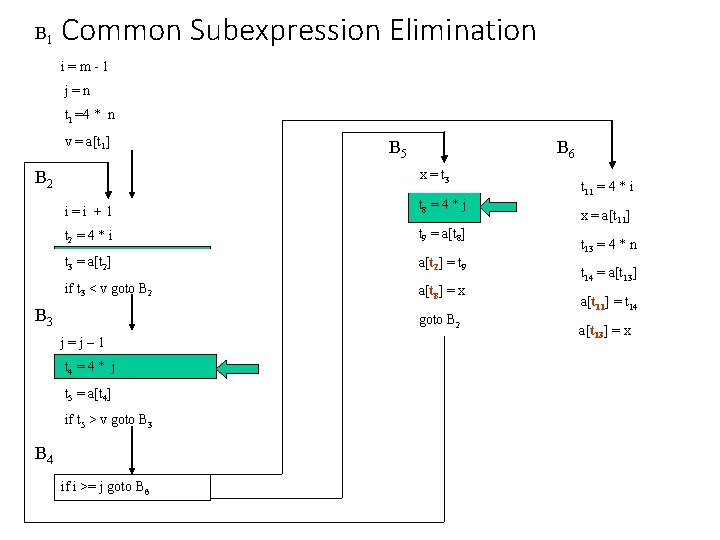
B 1 Common Subexpression Elimination i=m-1 j=n t 1 =4 * n v = a[t 1] B 5 B 6 x = t 3 B 2 i=i +1 t 8 = 4 * j t 2 = 4 * i t 9 = a[t 8] t 3 = a[t 2] = t 9 if t 3 < v goto B 2 a[t 8] = x B 3 goto B 2 j=j– 1 t 4 = 4 * j t 5 = a[t 4] if t 5 > v goto B 3 B 4 if i >= j goto B 6 t 11 = 4 * i x = a[t 11] t 13 = 4 * n t 14 = a[t 13] a[t 11] = t 14 a[t 13] = x

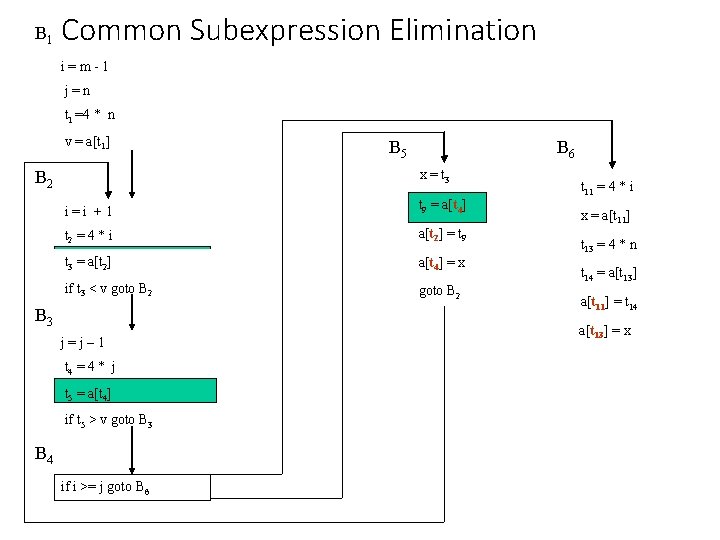
B 1 Common Subexpression Elimination i=m-1 j=n t 1 =4 * n v = a[t 1] B 5 B 6 x = t 3 B 2 i=i +1 t 9 = a[t 4] t 2 = 4 * i a[t 2] = t 9 t 3 = a[t 2] a[t 4] = x if t 3 < v goto B 2 B 3 j=j– 1 t 4 = 4 * j t 5 = a[t 4] if t 5 > v goto B 3 B 4 if i >= j goto B 6 t 11 = 4 * i x = a[t 11] t 13 = 4 * n t 14 = a[t 13] a[t 11] = t 14 a[t 13] = x

B 1 Common Subexpression Elimination i=m-1 j=n t 1 =4 * n v = a[t 1] B 5 B 6 x = t 3 B 2 i=i +1 a[t 2] = t 5 t 2 = 4 * i a[t 4] = x t 3 = a[t 2] goto B 2 if t 3 < v goto B 2 B 3 j=j– 1 t 4 = 4 * j t 5 = a[t 4] if t 5 > v goto B 3 B 4 if i >= j goto B 6 t 11 = 4 * i x = a[t 11] t 13 = 4 * n t 14 = a[t 13] a[t 11] = t 14 a[t 13] = x

B 1 Common Subexpression Elimination i=m-1 j=n t 1 =4 * n v = a[t 1] B 5 B 6 x = t 3 B 2 i=i +1 a[t 2] = t 5 t 2 = 4 * i a[t 4] = x t 3 = a[t 2] goto B 2 if t 3 < v goto B 2 B 3 j=j– 1 t 4 = 4 * j t 5 = a[t 4] if t 5 > v goto B 3 B 4 if i >= j goto B 6 x = t 3 t 14 = a[t 1] a[t 2] = t 14 a[t 1] = x Similarly for B 6

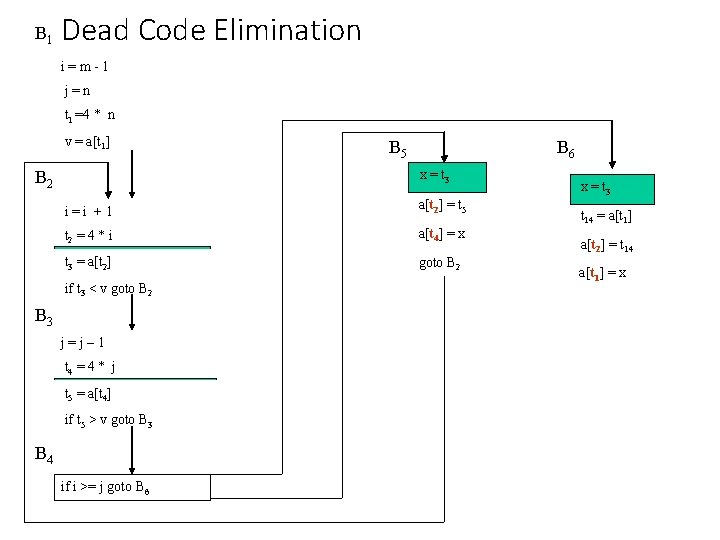
B 1 Dead Code Elimination i=m-1 j=n t 1 =4 * n v = a[t 1] B 5 B 6 x = t 3 B 2 i=i +1 a[t 2] = t 5 t 2 = 4 * i a[t 4] = x t 3 = a[t 2] goto B 2 if t 3 < v goto B 2 B 3 j=j– 1 t 4 = 4 * j t 5 = a[t 4] if t 5 > v goto B 3 B 4 if i >= j goto B 6 x = t 3 t 14 = a[t 1] a[t 2] = t 14 a[t 1] = x

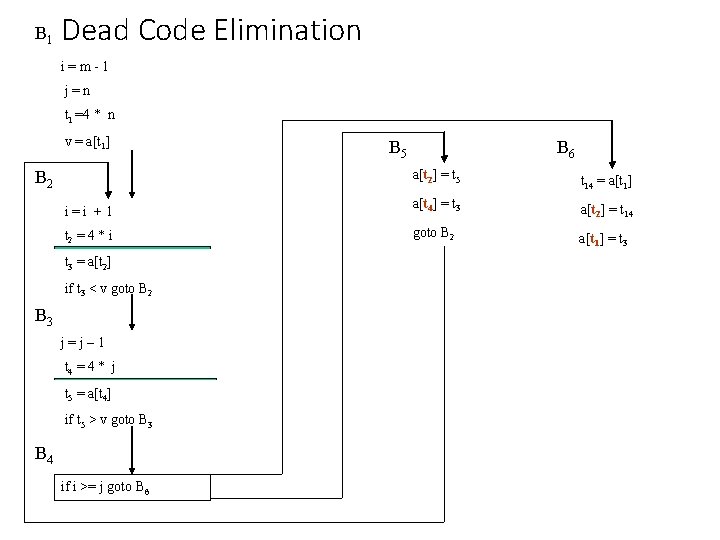
B 1 Dead Code Elimination i=m-1 j=n t 1 =4 * n v = a[t 1] B 5 B 6 a[t 2] = t 5 t 14 = a[t 1] i=i +1 a[t 4] = t 3 a[t 2] = t 14 t 2 = 4 * i goto B 2 a[t 1] = t 3 B 2 t 3 = a[t 2] if t 3 < v goto B 2 B 3 j=j– 1 t 4 = 4 * j t 5 = a[t 4] if t 5 > v goto B 3 B 4 if i >= j goto B 6

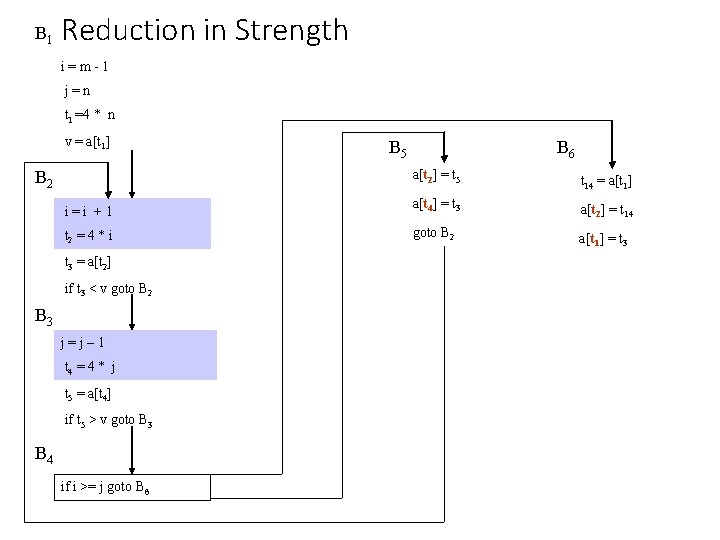
B 1 Reduction in Strength i=m-1 j=n t 1 =4 * n v = a[t 1] B 5 B 6 a[t 2] = t 5 t 14 = a[t 1] i=i +1 a[t 4] = t 3 a[t 2] = t 14 t 2 = 4 * i goto B 2 a[t 1] = t 3 B 2 t 3 = a[t 2] if t 3 < v goto B 2 B 3 j=j– 1 t 4 = 4 * j t 5 = a[t 4] if t 5 > v goto B 3 B 4 if i >= j goto B 6

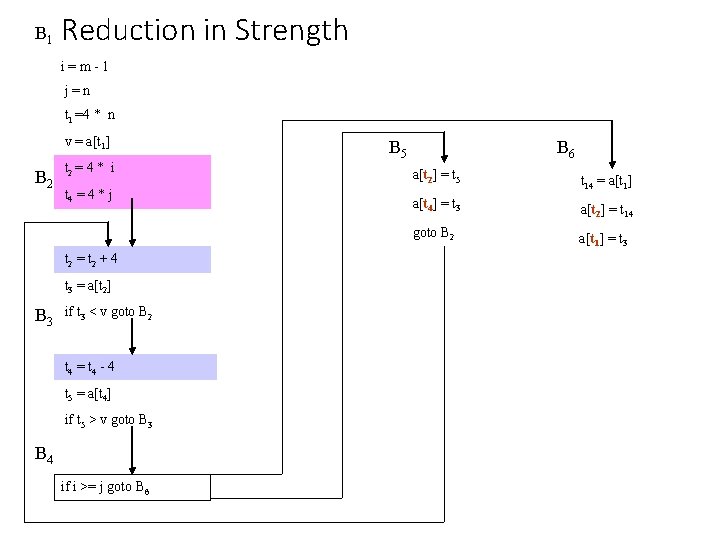
B 1 Reduction in Strength i=m-1 j=n t 1 =4 * n v = a[t 1] B 2 t 2 = 4 * i t 4 = 4 * j t 2 = t 2 + 4 t 3 = a[t 2] B 3 if t 3 < v goto B 2 t 4 = t 4 - 4 t 5 = a[t 4] if t 5 > v goto B 3 B 4 if i >= j goto B 6 B 5 B 6 a[t 2] = t 5 t 14 = a[t 1] a[t 4] = t 3 a[t 2] = t 14 goto B 2 a[t 1] = t 3

Thank You