Compiler Construction NFA DFA Construction Here our purpose

Compiler Construction

NFA → DFA Construction Here our purpose is not only to study therotical concepts but to see how they are implemented. The algorithm is called subset construction. In the transition table of an NFA, each entry is a set of states. In DFA, each entry is a single state The general idea behind NFA-to-DFA construction is that each DFA state corresponds to a set of NFA states. The DFA uses its state to keep track of all possible states the NFA can be in after reading each input symbol. 2

NFA → DFA Construction We will use the following operations. e-closure(T): set of NFA states reachable from some NFA state s in T on etransitions alone. move(T, a): set of NFA states to which there is a transition on input a from some NFA state s in set of states T. 3

NFA → DFA Construction Step 1: Before it sees the first input symbol, NFA can be in any of the state in the set e-closure(s 0), where s 0 is the start state of the NFA. Step 2: Suppose that exactly the states in set T are reachable from s 0 on a given sequence of input symbols(other than e). Let a be the next input symbol. 4

NFA → DFA Construction • On seeing a, the NFA can move to any of the states in the set move(T, a). • When we allow for e-transitions, NFA can be in any of the states in e-closure(move(T, a)) after seeing a. 5

Subset Construction Algorithm: Input: NFA N with state set S, alphabet S, start state s 0, final states F Output: DFA D with state set S’, alphabet S, start states s 0’ = e-closure(s 0), final states F’, transition table: S’ x S → S’ i. e. We remain in S’ by consuming any of the S 6

Algorithm // initially, e-closure(s 0) is the only // state in D states S’ and it is // unmarked s 0’ = e-closure(s 0) S’ = {s 0’ } (unmarked) We will keep on marking states as v move in the algo s 0’ is the first member of S’ Remember S’ has set of states as members 7

while there is some unmarked state T in S’ mark state T for all a in S do U = e-closure( move(T, a) ); //U is a set of states if U not already in S’ add U as an unmarked state to S’ Dtran(T, a) = U; // 2 d table Rows=T, Col=a end for end while 8

Algorithm F’: for each DFA state S if S contains an NFA final state mark S as DFA final state 9

Subset Construction Example 0 e e 2 a e 3 6 1 e e 4 b e 5 e 7 a 8 b 9 b 10 e NFA for (a | b )*abb 10

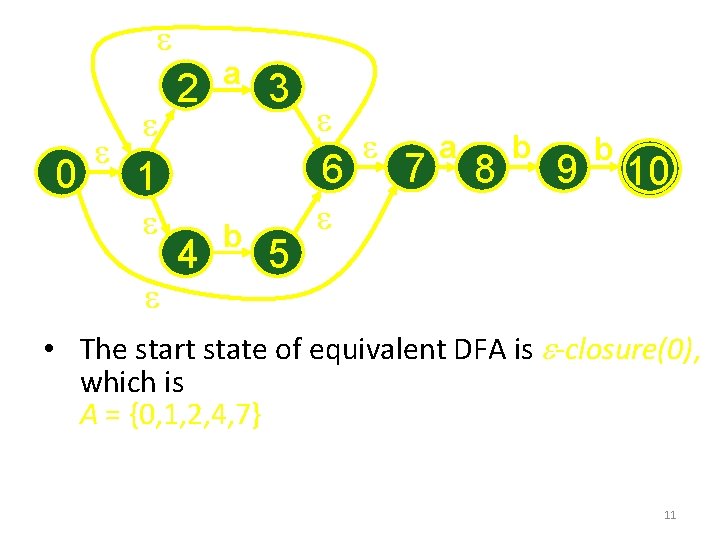
e 0 e e 2 e a 3 6 1 e e e 4 b 5 e e 7 a 8 b 9 b 10 • The start state of equivalent DFA is e-closure(0), which is A = {0, 1, 2, 4, 7} 11

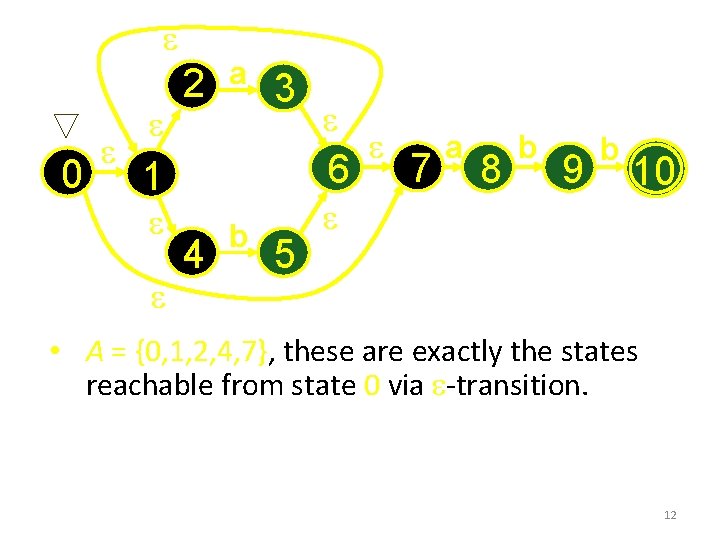
e 0 e e 2 e a 3 6 1 e e e 4 b 5 e e 7 a 8 b 9 b 10 • A = {0, 1, 2, 4, 7}, these are exactly the states reachable from state 0 via e-transition. 12

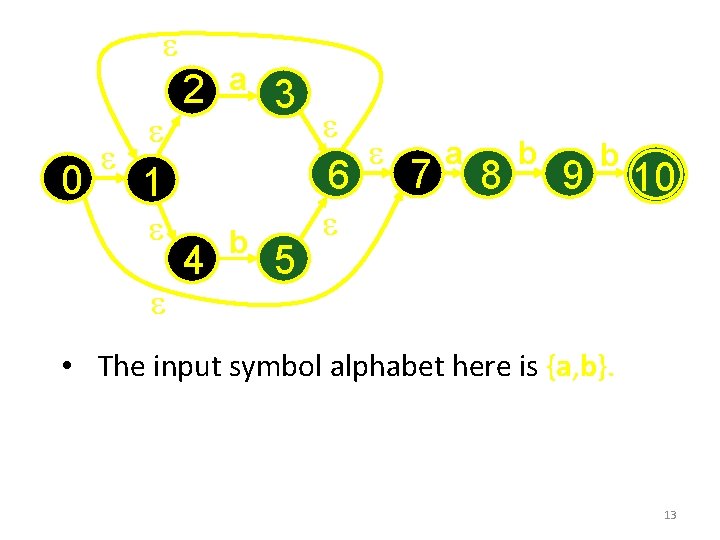
e 0 e e 2 e a 3 6 1 e e e 4 b 5 e 7 a 8 b 9 b e 10 • The input symbol alphabet here is {a, b}. 13

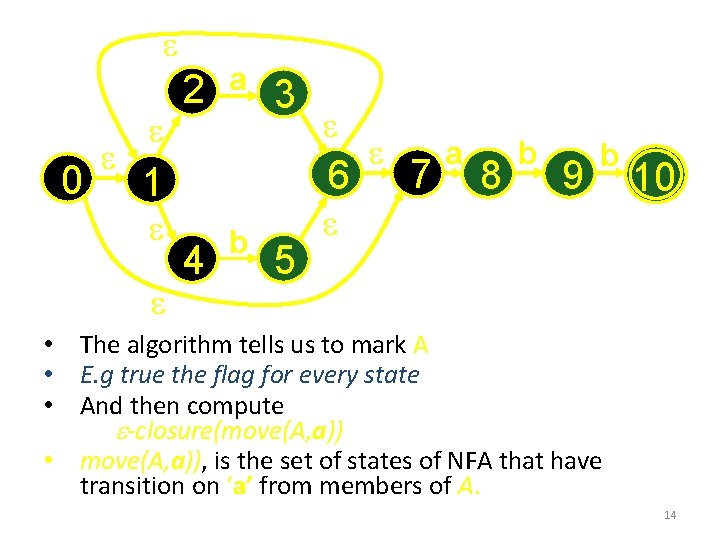
e 0 e e 2 e a 3 6 1 e e e 4 b 5 e 7 a 8 b 9 b e 10 • The algorithm tells us to mark A • E. g true the flag for every state • And then compute e-closure(move(A, a)) • move(A, a)), is the set of states of NFA that have transition on ‘a’ from members of A. 14

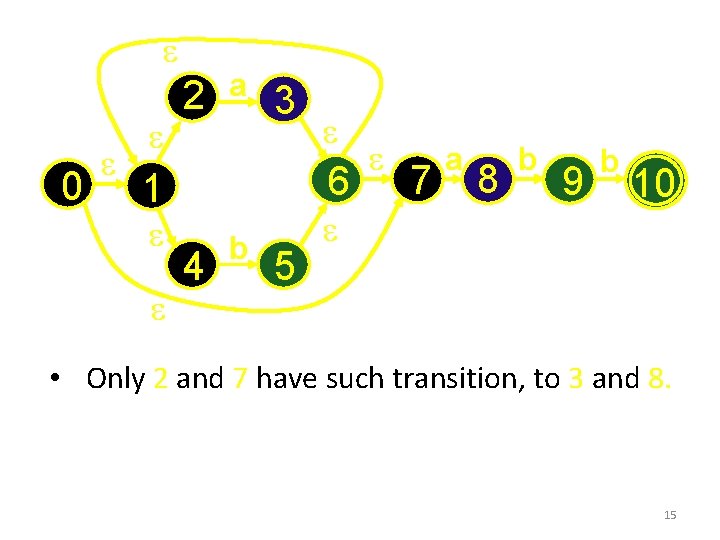
e 0 e e 2 e a 3 6 1 e e e 4 b 5 e e 7 a 8 b 9 b 10 • Only 2 and 7 have such transition, to 3 and 8. 15

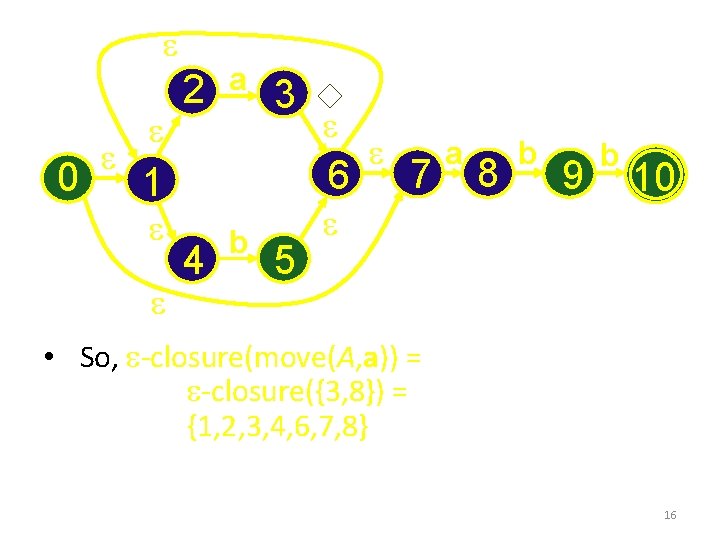
e 0 e e 2 e a 3 6 1 e e e 4 b 5 e 7 e a 8 b 9 b 10 • So, e-closure(move(A, a)) = e-closure({3, 8}) = {1, 2, 3, 4, 6, 7, 8} 16

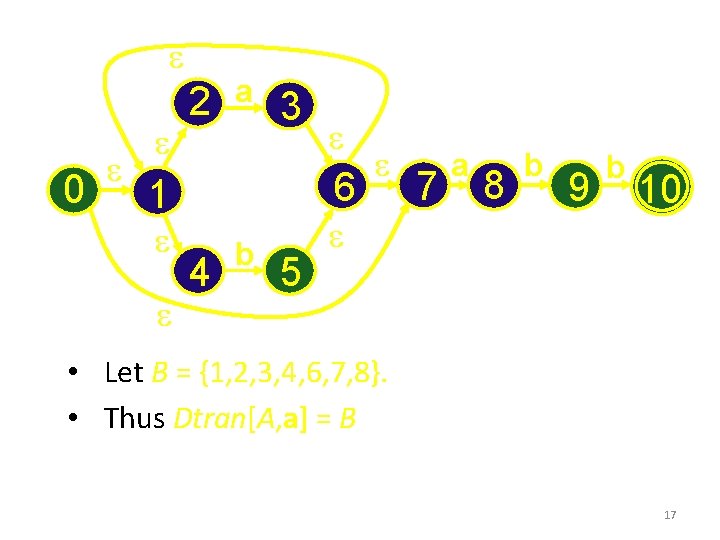
e 0 e e 2 e a 3 6 1 e e e 4 b 5 e e 7 a 8 b 9 b 10 • Let B = {1, 2, 3, 4, 6, 7, 8}. • Thus Dtran[A, a] = B 17

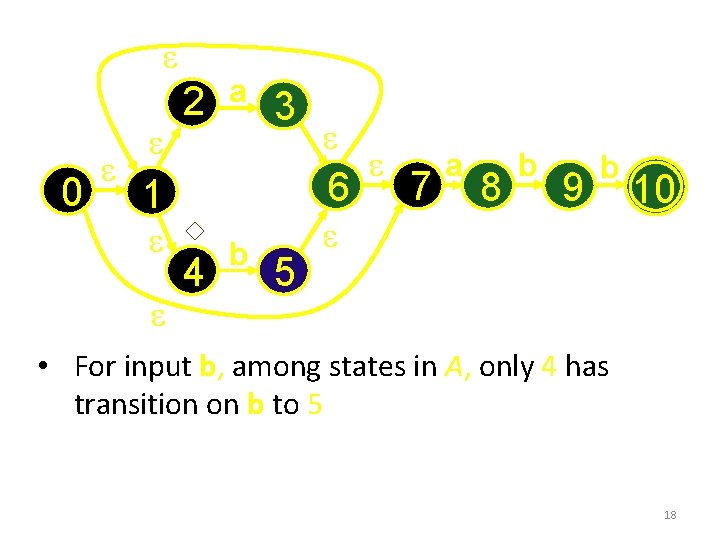
e 0 e e 2 e a 3 6 1 e e e 4 b 5 e 7 a 8 b 9 b e 10 • For input b, among states in A, only 4 has transition on b to 5 18

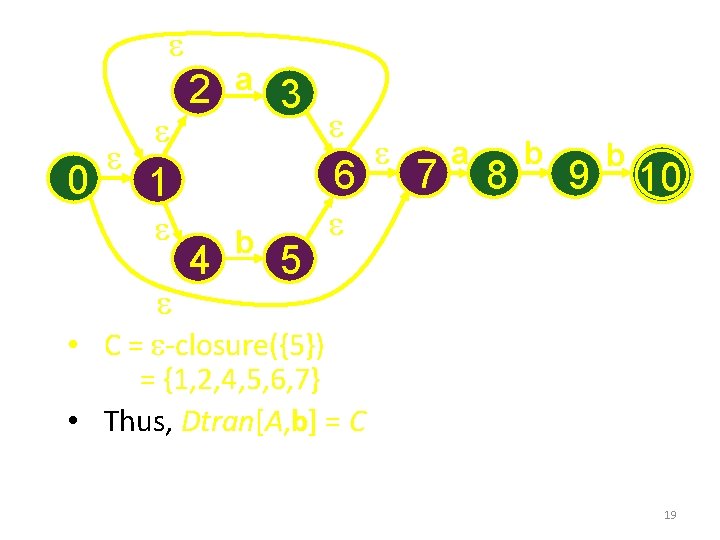
e 0 e e 2 e a 3 6 1 e e e 4 b 5 e e 7 a 8 b 9 b 10 • C = e-closure({5}) = {1, 2, 4, 5, 6, 7} • Thus, Dtran[A, b] = C 19

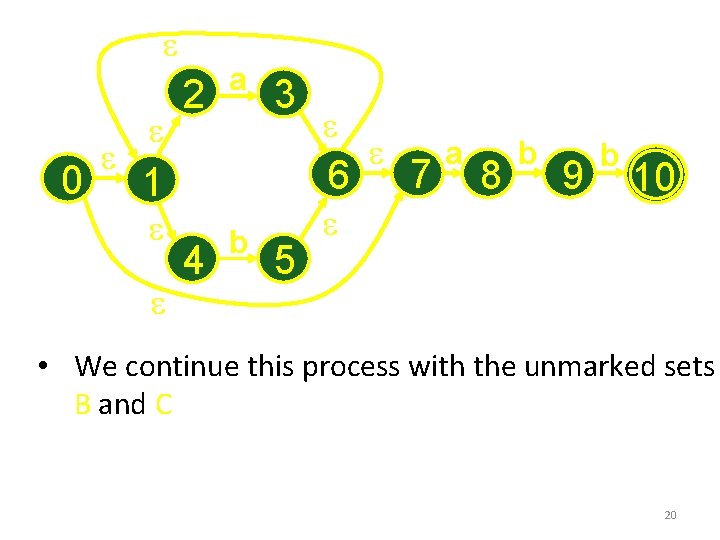
e 0 e e 2 e a 3 6 1 e e e 4 b 5 e e 7 a 8 b 9 b 10 • We continue this process with the unmarked sets B and C 20

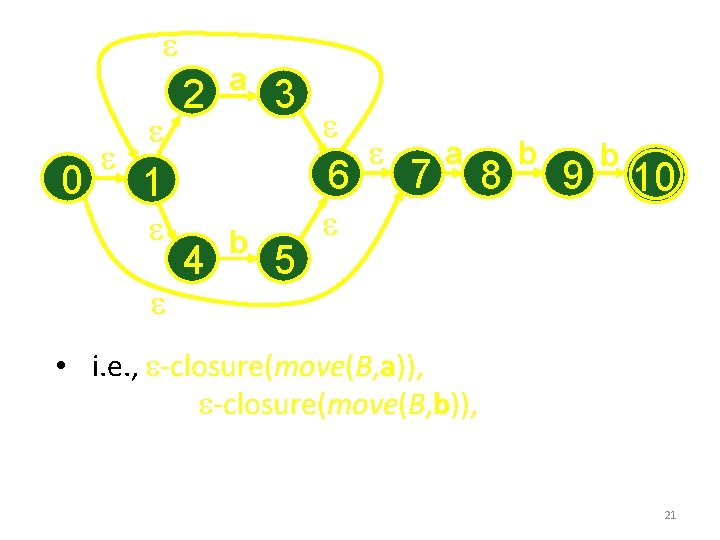
e 0 e e 2 e a 3 6 1 e e e 4 b 5 e 7 a e 8 b 9 b 10 • i. e. , e-closure(move(B, a)), e-closure(move(B, b)), 21

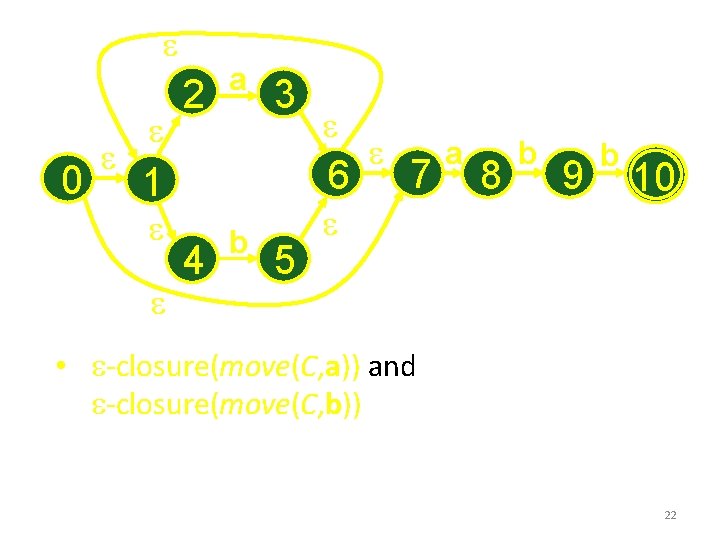
e 0 e e 2 e a 3 6 1 e e e 4 b 5 e 7 e a 8 b 9 b 10 • e-closure(move(C, a)) and e-closure(move(C, b)) 22

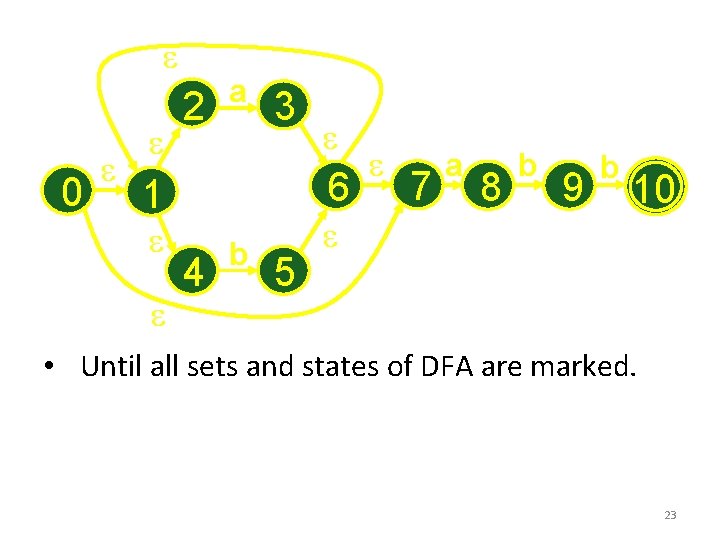
e 0 e e 2 e a 3 6 1 e e e 4 b 5 e e 7 a 8 b 9 b 10 • Until all sets and states of DFA are marked. 23

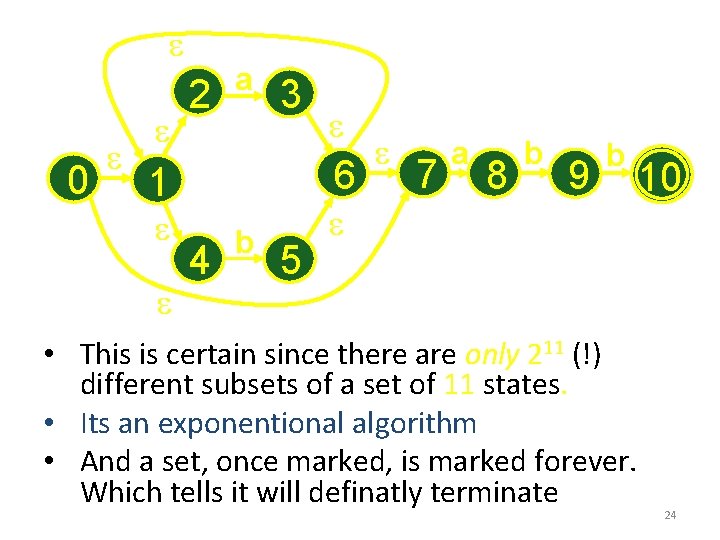
e 0 e e 2 e a 3 6 1 e e e 4 b 5 e 7 a 8 b 9 b e • This is certain since there are only 211 (!) different subsets of a set of 11 states. • Its an exponentional algorithm • And a set, once marked, is marked forever. Which tells it will definatly terminate 10 24

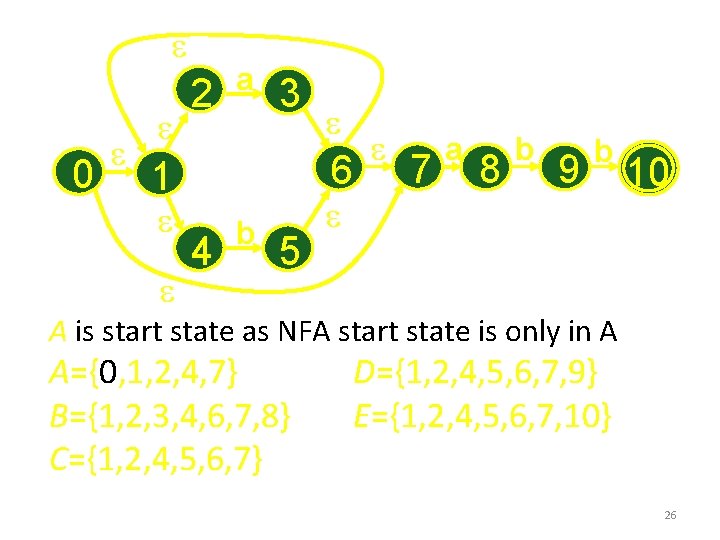
Subset Construction Eventually, the 5 sets are: A={0, 1, 2, 4, 7} B={1, 2, 3, 4, 6, 7, 8} C={1, 2, 4, 5, 6, 7} D={1, 2, 4, 5, 6, 7, 9} E={1, 2, 4, 5, 6, 7, 10} 25

e 0 e e 2 e a 3 6 1 e e e 4 b 5 e e 7 a 8 b 9 b 10 A is start state as NFA start state is only in A A={0, 1, 2, 4, 7} B={1, 2, 3, 4, 6, 7, 8} C={1, 2, 4, 5, 6, 7} D={1, 2, 4, 5, 6, 7, 9} E={1, 2, 4, 5, 6, 7, 10} 26

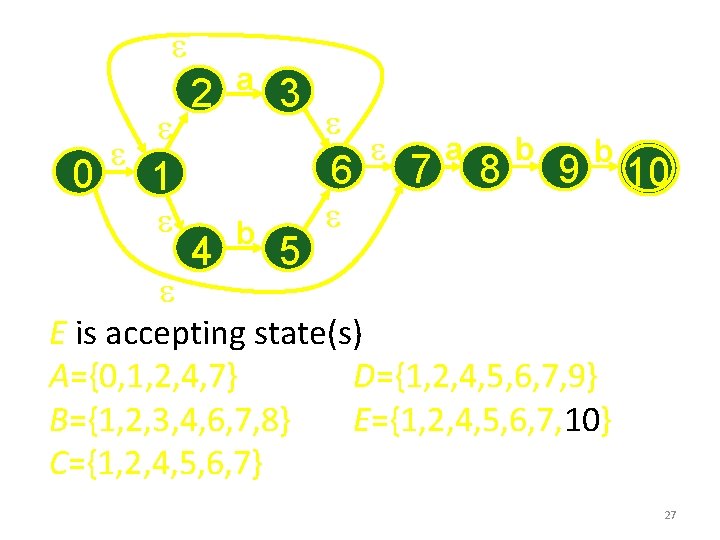
e 0 e e 2 e a 3 6 1 e e 4 b 5 e e 7 a 8 b 9 b 10 e E is accepting state(s) A={0, 1, 2, 4, 7} D={1, 2, 4, 5, 6, 7, 9} B={1, 2, 3, 4, 6, 7, 8} E={1, 2, 4, 5, 6, 7, 10} C={1, 2, 4, 5, 6, 7} 27

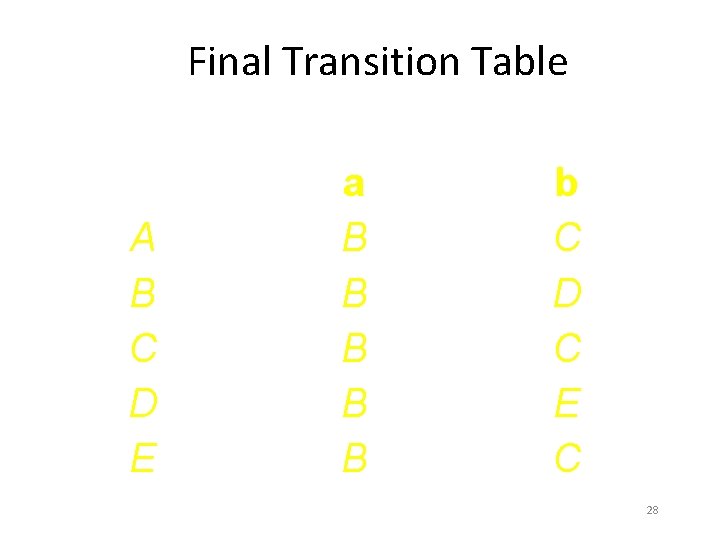
Final Transition Table State A B C D E Input symbol a b B C B D B C B E B C 28

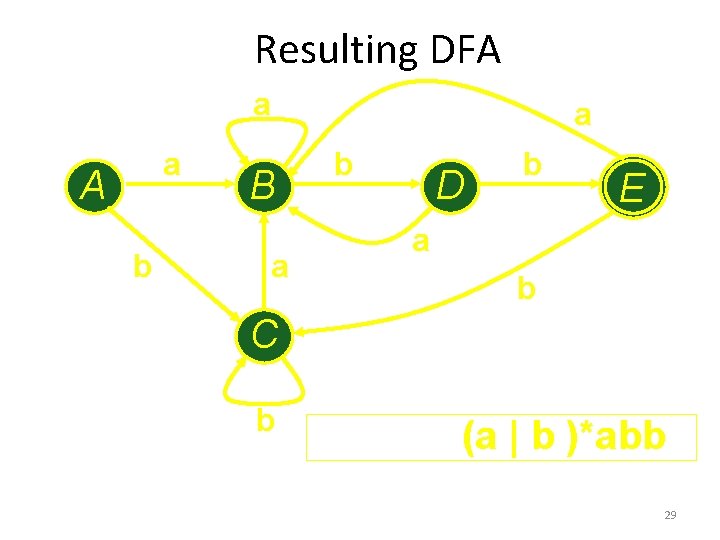
Resulting DFA a a A b a B a b D b E a b C b DFA for (a | b )*abb 29

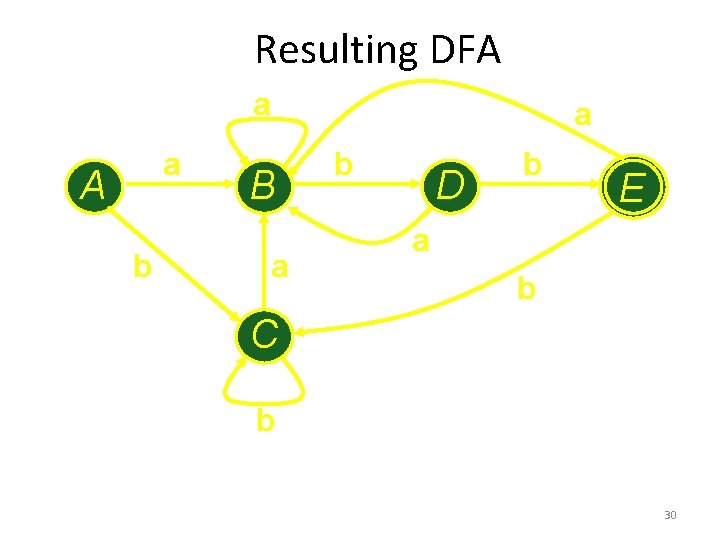
Resulting DFA a a A b a B a b D b E a b C b a a b b 30