Competitive behavior in multiagent systems EEL 5708 What

Competitive behavior in multi-agent systems EEL 5708

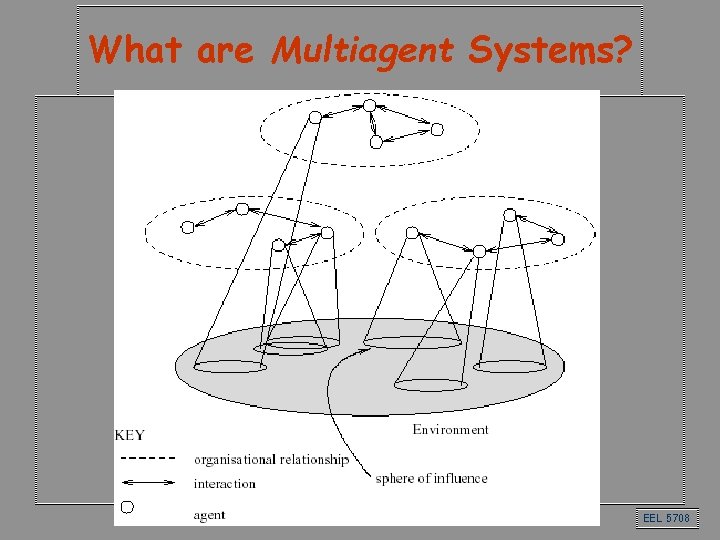
What are Multiagent Systems? EEL 5708

Multi. Agent Systems Thus a multiagent system contains a number • • of agents… …which interact through communication… …are able to act in an environment… …have different “spheres of influence” (which may coincide)… …will be linked by other (organizational) relationships EEL 5708

Utilities and Preferences • Assume we have just two agents: Ag = {i, j} • Agents are assumed to be self-interested: they have preferences over how the environment is • Assume W = {w 1, w 2, …}is the set of “outcomes” that agents have preferences over • We capture preferences by utility functions: ui = W ú uj = W ú • Utility functions lead to preference orderings over outcomes: w š i w’ means ui(w) $ ui(w’) w ™i w’ means ui(w) > ui(w’) EEL 5708

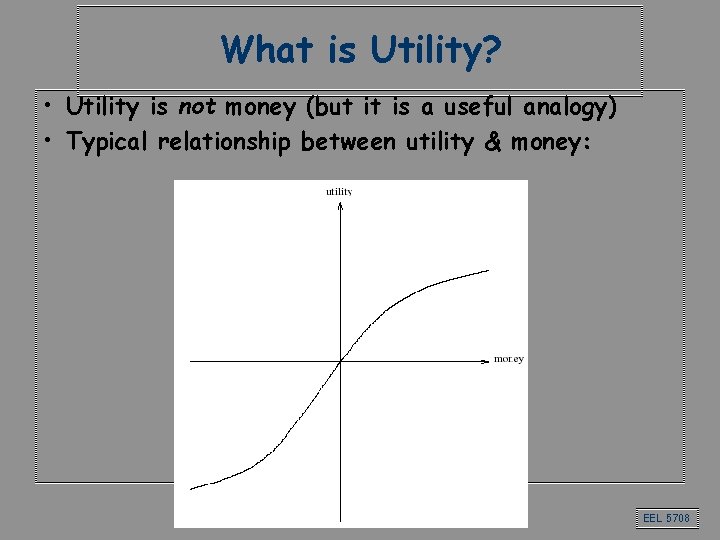
What is Utility? • Utility is not money (but it is a useful analogy) • Typical relationship between utility & money: EEL 5708

Multiagent Encounters • We need a model of the environment in which these agents will act… – agents simultaneously choose an action to perform, and as a result of the actions they select, an outcome in W will result – the actual outcome depends on the combination of actions – assume each agent has just two possible actions that it can perform, C (“cooperate”) and D (“defect”) • Environment behavior given by state transformer function: EEL 5708

Multiagent Encounters • Here is a state transformer function: (This environment is sensitive to actions of both agents. ) • Here is another: (Neither agent has any influence in this environment. ) • And here is another: (This environment is controlled by j. ) EEL 5708

Rational Action • Suppose we have the case where both agents can influence the outcome, and they have utility functions as follows: • With a bit of abuse of notation: • Then agent i’s preferences are: • “C” is the rational choice for i. (Because i prefers all outcomes that arise through C over all outcomes that arise through D. ) EEL 5708

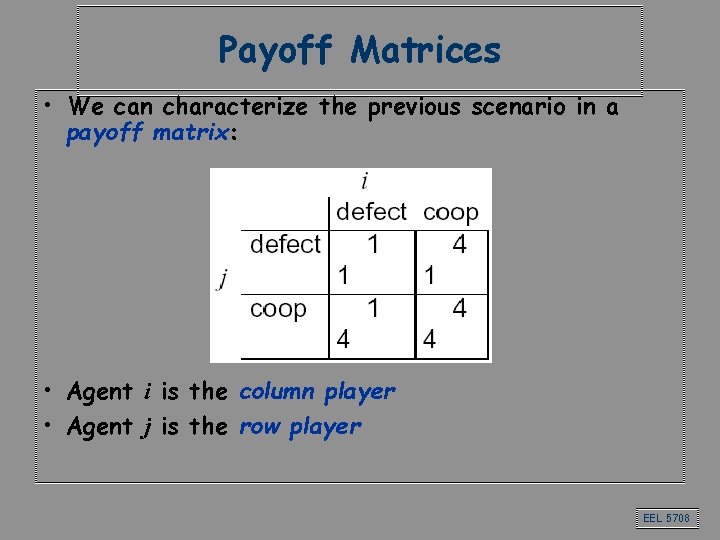
Payoff Matrices • We can characterize the previous scenario in a payoff matrix: • Agent i is the column player • Agent j is the row player EEL 5708

Dominant Strategies • Given any particular strategy (either C or D) of agent i, there will be a number of possible outcomes • We say s 1 dominates s 2 if every outcome possible by i playing s 1 is preferred over every outcome possible by i playing s 2 • A rational agent will never play a dominated strategy • So in deciding what to do, we can delete dominated strategies • Unfortunately, there isn’t always a unique undominated strategy EEL 5708

Nash Equilibrium • • • In general, we will say that two strategies s 1 and s 2 are in Nash equilibrium if: 1. under the assumption that agent i plays s 1, agent j can do no better than play s 2; and 2. under the assumption that agent j plays s 2, agent i can do no better than play s 1. Neither agent has any incentive to deviate from a Nash equilibrium Unfortunately: 1. Not every interaction scenario has a Nash equilibrium 2. Some interaction scenarios have more than one Nash equilibrium EEL 5708

Competitive and Zero-Sum Interactions • Where preferences of agents are diametrically opposed we have strictly competitive scenarios • Zero-sum encounters are those where utilities sum to zero: u i (w ) + u j (w ) = 0 for all w 0 W • Zero sum implies strictly competitive • Zero sum encounters in real life are very rare … but people tend to act in many scenarios as if they were zero sum EEL 5708

The Prisoner’s Dilemma • Two men are collectively charged with a crime and held in separate cells, with no way of meeting or communicating. They are told that: – if one confesses and the other does not, the confessor will be freed, and the other will be jailed for three years – if both confess, then each will be jailed for two years • Both prisoners know that if neither confesses, then they will each be jailed for one year EEL 5708

The Prisoner’s Dilemma • Payoff matrix for prisoner’s dilemma: • Top left: If both defect, then both get punishment for mutual defection • Top right: If i cooperates and j defects, i gets sucker’s payoff of 1, while j gets 4 • Bottom left: If j cooperates and i defects, j gets sucker’s payoff of 1, while i gets 4 • Bottom right: Reward for mutual cooperation EEL 5708

The Prisoner’s Dilemma • The individual rational action is defect This guarantees a payoff of no worse than 2, whereas cooperating guarantees a payoff of at most 1 • So defection is the best response to all possible strategies: both agents defect, and get payoff = 2 • But intuition says this is not the best outcome: Surely they should both cooperate and each get payoff of 3! EEL 5708

The Prisoner’s Dilemma • This apparent paradox is the fundamental problem of multi-agent interactions. It appears to imply that cooperation will not occur in societies of self-interested agents. • Real world examples: – nuclear arms reduction (“why don’t I keep mine. . . ”) – free rider systems — public transport; – in the UK — television licenses. • The prisoner’s dilemma is ubiquitous. • Can we recover cooperation? EEL 5708

Arguments for Recovering Cooperation • Conclusions that some have drawn from this analysis: – the game theory notion of rational action is wrong! – somehow the dilemma is being formulated wrongly • Arguments to recover cooperation: – We are not all Machiavelli! – The other prisoner is my twin! – The shadow of the future… EEL 5708

The Iterated Prisoner’s Dilemma • One answer: play the game more than once • If you know you will be meeting your opponent again, then the incentive to defect appears to evaporate • Cooperation is the rational choice in the infinititely repeated prisoner’s dilemma (Hurrah!) EEL 5708

Backwards Induction • But…suppose you both know that you will play the game exactly n times On round n - 1, you have an incentive to defect, to gain that extra bit of payoff… But this makes round n – 2 the last “real”, and so you have an incentive to defect there, too. This is the backwards induction problem. • Playing the prisoner’s dilemma with a fixed, finite, pre-determined, commonly known number of rounds, defection is the best strategy EEL 5708

Axelrod’s Tournament • Suppose you play iterated prisoner’s dilemma against a range of opponents… What strategy should you choose, so as to maximize your overall payoff? • Axelrod (1984) investigated this problem, with a computer tournament for programs playing the prisoner’s dilemma EEL 5708

• • – ALLD: Strategies in Axelrod’s Tournament “Always defect” — the hawk strategy; TIT-FOR-TAT: 1. On round u = 0, cooperate 2. On round u > 0, do what your opponent did on round u – 1 – – TESTER: On 1 st round, defect. If the opponent retaliated, then play TIT-FORTAT. Otherwise intersperse cooperation and defection. JOSS: As TIT-FOR-TAT, except periodically defect EEL 5708

Recipes for Success in Axelrod’s Tournament • Axelrod suggests the following rules for succeeding in his tournament: – Don’t be envious: Don’t play as if it were zero sum! – Be nice: Start by cooperating, and reciprocate cooperation – Retaliate appropriately: Always punish defection immediately, but use “measured” force — don’t overdo it – Don’t hold grudges: Always reciprocate cooperation immediately EEL 5708

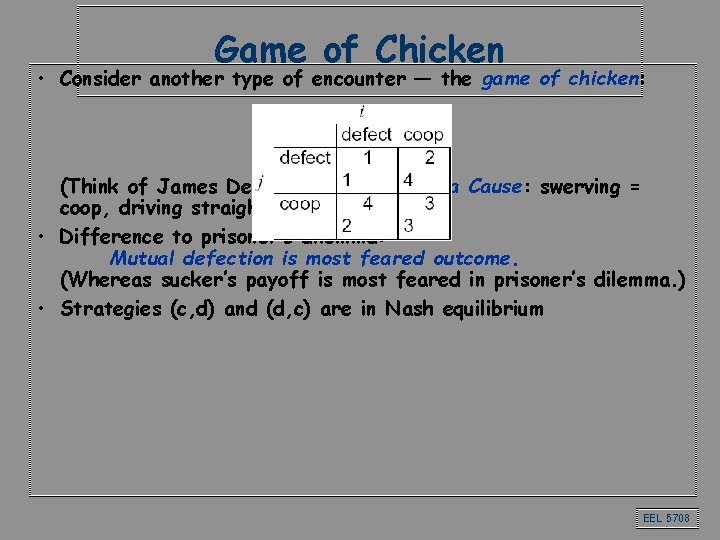
Game of Chicken • Consider another type of encounter — the game of chicken: (Think of James Dean in Rebel without a Cause: swerving = coop, driving straight = defect. ) • Difference to prisoner’s dilemma: Mutual defection is most feared outcome. (Whereas sucker’s payoff is most feared in prisoner’s dilemma. ) • Strategies (c, d) and (d, c) are in Nash equilibrium EEL 5708

Other Symmetric 2 x 2 Games • Given the 4 possible outcomes of (symmetric) cooperate/defect games, there are 24 possible orderings on outcomes – CC š i CD š i DC š i DD Cooperation dominates – DC š i DD š i CC š i CD Deadlock. You will always do best by defecting – DC š i CC š i DD š i CD Prisoner’s dilemma – DC š i CD š i DD Chicken – CC š i DD š i CD Stag hunt EEL 5708

Reaching Agreements • How do agents reaching agreements when they are self interested? • In an extreme case (zero sum encounter) no agreement is possible — but in most scenarios, there is potential for mutually beneficial agreement on matters of common interest • The capabilities of negotiation and argumentation are central to the ability of an agent to reach such agreements EEL 5708

Mechanisms, Protocols, and Strategies • Negotiation is governed by a particular mechanism, or protocol • The mechanism defines the “rules of encounter” between agents • Mechanism design is designing mechanisms so that they have certain desirable properties • Given a particular protocol, how can a particular strategy be designed that individual agents can use? EEL 5708

Mechanism Design • Desirable properties of mechanisms: – – – – Convergence/guaranteed success Maximizing social welfare Pareto efficiency Individual rationality Stability Simplicity Distribution EEL 5708

Auctions • An auction takes place between an agent known as the auctioneer and a collection of agents known as the bidders • The goal of the auction is for the auctioneer to allocate the good to one of the bidders • In most settings the auctioneer desires to maximize the price; bidders desire to minimize price EEL 5708

Auction Parameters • Goods can have – private value – public/common value – correlated value • Winner determination may be – first price – second price • Bids may be – open cry – sealed bid • Bidding may be – one shot – ascending – descending EEL 5708

English Auctions • Most commonly known type of auction: – first price – open cry – ascending • Dominant strategy is for agent to successively bid a small amount more than the current highest bid until it reaches their valuation, then withdraw • Susceptible to: – winner’s curse – shills EEL 5708

Dutch Auctions • Dutch auctions are examples of open-cry descending auctions: – auctioneer starts by offering good at artificially high value – auctioneer lowers offer price until some agent makes a bid equal to the current offer price – the good is then allocated to the agent that made the offer EEL 5708

First-Price Sealed-Bid Auctions • First-price sealed-bid auctions are one-shot auctions: – – there is a single round bidders submit a sealed bid for the good is allocated to agent that made highest bid winner pays price of highest bid • Best strategy is to bid less than true valuation EEL 5708

Vickrey Auctions • Vickrey auctions are: – second-price – sealed-bid • Good is awarded to the agent that made the highest bid; at the price of the second highest bid • Bidding to your true valuation is dominant strategy in Vickrey auctions • Vickrey auctions susceptible to antisocial behavior EEL 5708

Lies and Collusion • The various auction protocols are susceptible to lying on the part of the auctioneer, and collusion among bidders, to varying degrees • All four auctions (English, Dutch, First-Price Sealed Bid, Vickrey) can be manipulated by bidder collusion • A dishonest auctioneer can exploit the Vickrey auction by lying about the 2 nd-highest bid • Shills can be introduced to inflate bidding prices in English auctions EEL 5708

Negotiation • Auctions are only concerned with the allocation of goods: richer techniques for reaching agreements are required • Negotiation is the process of reaching agreements on matters of common interest • Any negotiation setting will have four components: – – A negotiation set: possible proposals that agents can make A protocol Strategies, one for each agent, which are private A rule that determines when a deal has been struck and what the agreement deal is • Negotiation usually proceeds in a series of rounds, with every agent making a proposal at every round EEL 5708

Negotiation in Task-Oriented Imagine that you have three Domains children, each of whom needs to be delivered to a different school each morning. Your neighbor has four children, and also needs to take them to school. Delivery of each child can be modeled as an indivisible task. You and your neighbor can discuss the situation, and come to an agreement that it is better for both of you (for example, by carrying the other’s child to a shared destination, saving him the trip). There is no concern about being able to achieve your task by yourself. The worst that can happen is that you and your neighbor won’t come to an agreement about setting up a car pool, in which case you are no worse off than if you were alone. You can only benefit (or do no worse) from your neighbor’s tasks. Assume, though, that one of my children and one of my neighbors’ children both go to the same school (that is, the cost of carrying out these two deliveries, or two tasks, is the same as the cost of carrying out one of them). It obviously makes sense for both children to be taken together, and only my neighbor or I will need to make the trip to carry out both tasks. --- Rules of Encounter, Rosenschein and Zlotkin, 1994 EEL 5708

Machines Controlling and Sharing Resources • Electrical grids (load balancing) • Telecommunications networks (routing) • PDA’s (schedulers) • Shared databases (intelligent access) • Traffic control (coordination) EEL 5708

Heterogeneous, Self-motivated Agents The systems: • are not centrally designed • do not have a notion of global utility • are dynamic (e. g. , new types of agents) • will not act “benevolently” unless it is in their interest to do so EEL 5708

The Aim of the Research • Social engineering for communities of machines – The creation of interaction environments that foster certain kinds of social behavior The exploitation of game theory tools for high-level protocol design EEL 5708

Broad Working Assumption • Designers (from different companies, countries, etc. ) come together to agree on standards for how their automated agents will interact (in a given domain) • Discuss various possibilities and their tradeoffs, and agree on protocols, strategies, and social laws to be implemented in their machines EEL 5708

Attributes of Standards ü Efficient: Pareto Optimal ü Stable: No incentive to deviate ü Simple: Low computational and communication cost ü Distributed: No central decision-maker ü Symmetric: Agents play equivalent roles Designing protocols for specific classes of domains that satisfy some or all of these attributes EEL 5708

Distributed Artificial Intelligence (DAI) • Distributed Problem Solving (DPS) – Centrally designed systems, built-in cooperation, have global problem to solve ü Multi-Agent Systems (MAS) ü Group of utility-maximizing heterogeneous agents co-existing in same environment, possibly competitive EEL 5708

Phone Call Competition Example • Customer wishes to place long-distance call • Carriers simultaneously bid, sending proposed prices • Phone automatically chooses the carrier (dynamically) MCI $0. 18 AT&T $0. 20 Sprint $0. 23 EEL 5708

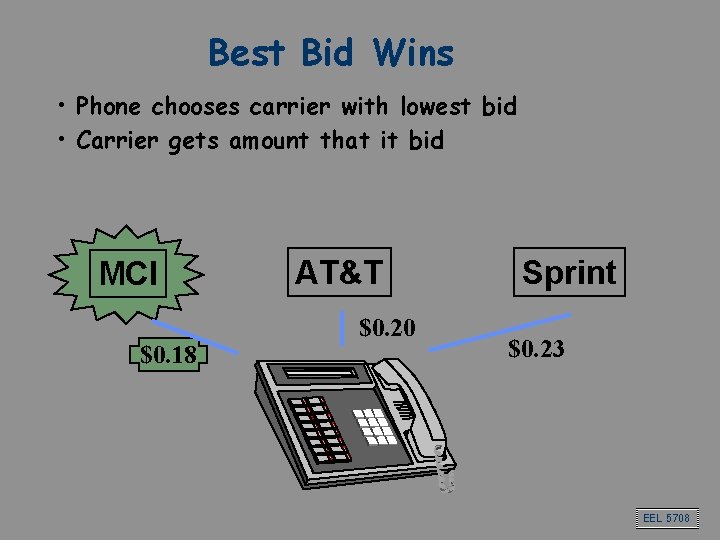
Best Bid Wins • Phone chooses carrier with lowest bid • Carrier gets amount that it bid MCI $0. 18 AT&T $0. 20 Sprint $0. 23 EEL 5708

Attributes of the Mechanism ü ü û û û Distributed Symmetric Stable Simple Efficient Carriers have an incentive to invest effort in strategic behavior MCI “Maybe I can bid as high as $0. 21. . . ” $0. 18 AT&T $0. 20 Sprint $0. 23 EEL 5708

Best Bid Wins, Gets Second Price (Vickrey Auction) • Phone chooses carrier with lowest bid • Carrier gets amount of second-best price MCI $0. 18 AT&T $0. 20 Sprint $0. 23 EEL 5708

Attributes of the Vickrey Mechanism ü ü ü Distributed Symmetric Stable Simple Efficient Carriers have no incentive to invest effort in strategic behavior MCI “I have no reason to overbid. . . ” $0. 18 AT&T $0. 20 Sprint $0. 23 EEL 5708

Domain Theory • Task Oriented Domains w Agents have tasks to achieve à Task redistribution • State Oriented Domains w Goals specify acceptable final states w Side effects à Joint plan and schedules • Worth Oriented Domains w Function rating states’ acceptability à Joint plan, schedules, and goal relaxation EEL 5708

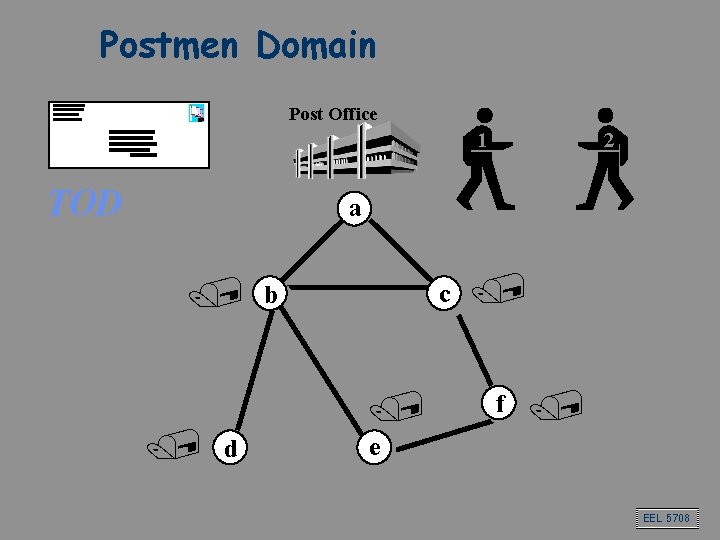
Postmen Domain Post Office 1 TOD 2 a / / c b / d / f / e EEL 5708

Database Domain TOD “All female employees making over $50, 000 a year. ” Common Database “All female employees with more than three children. ” 2 1 EEL 5708

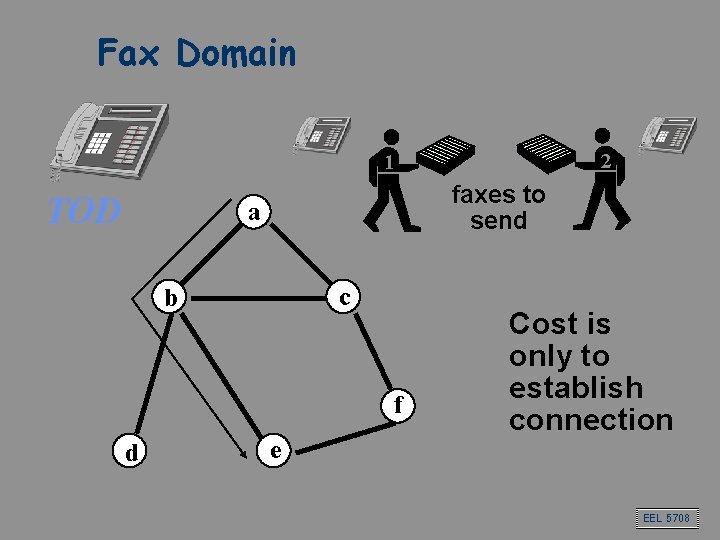
Fax Domain 2 1 TOD faxes to send a c b f d e Cost is only to establish connection EEL 5708

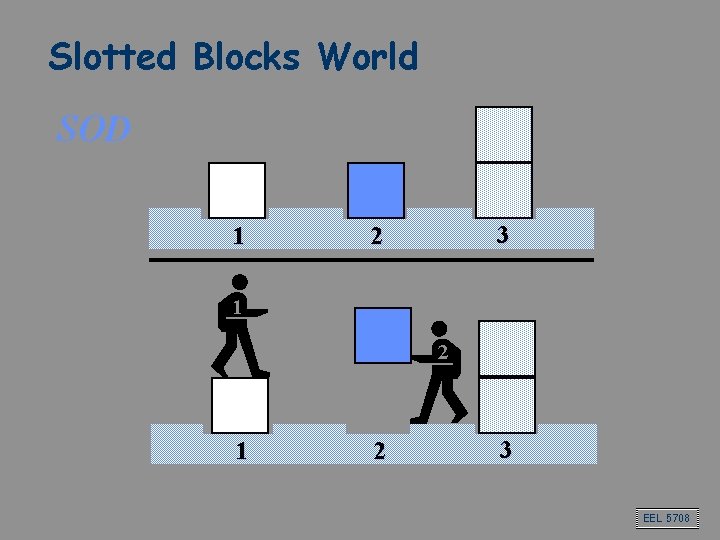
Slotted Blocks World SOD 1 3 2 1 2 3 EEL 5708

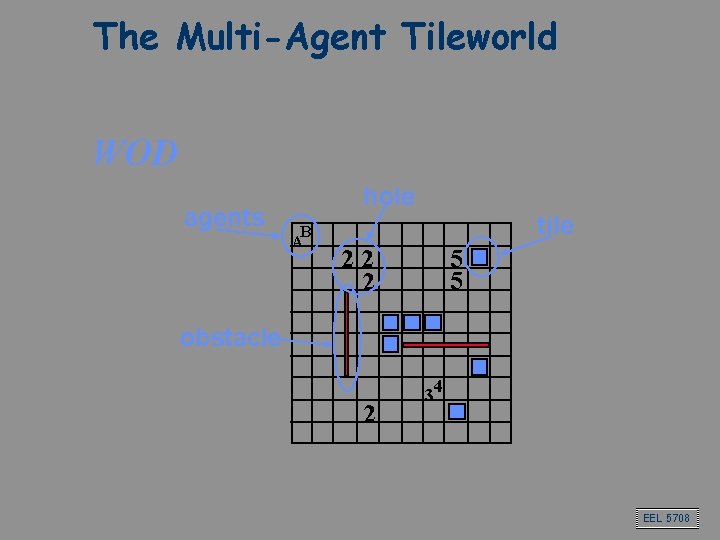
The Multi-Agent Tileworld WOD agents hole B A tile 22 2 5 5 obstacle 2 34 EEL 5708

TODs Defined • A TOD is a triple <T, Ag, c> where – T is the (finite) set of all possible tasks – Ag = {1, …, n} is the set of participating agents – c = Ã(T) ú + defines the cost of executing each subset of tasks • An encounter is a collection of tasks <T 1, …, Tn> where Ti Í T for each i Î Ag EEL 5708

Building Blocks ü Domain – A precise definition of what a goal is – Agent operations • Negotiation Protocol – A definition of a deal – A definition of utility – A definition of the conflict deal • Negotiation Strategy – In Equilibrium – Incentive-compatible EEL 5708

Deals in TODs • Given encounter <T 1, T 2>, a deal is an allocation of the tasks T 1 È T 2 to the agents 1 and 2 • The cost to i of deal d = <D 1, D 2> is c(Di), and will be denoted costi(d) • The utility of deal d to agent i is: utilityi(d) = c(Ti) – costi(d) • The conflict deal, Q, is the deal <T 1, T 2> consisting of the tasks originally allocated. Note that utilityi(Q) = 0 for all i Î Ag • Deal d is individual rational if it weakly dominates the conflict deal EEL 5708

The Negotiation Set • The set of deals over which agents negotiate are those that are: – individual rational – pareto efficient EEL 5708

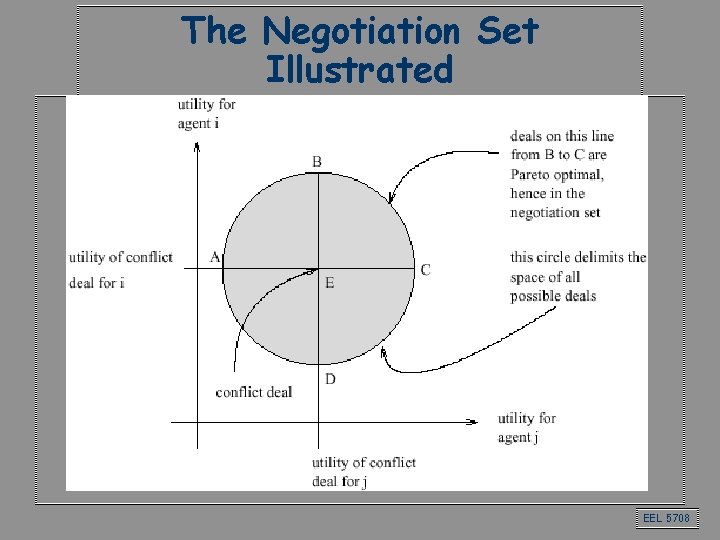
The Negotiation Set Illustrated EEL 5708

Negotiation Protocols • Agents use a product-maximizing negotiation protocol (as in Nash bargaining theory) • It should be a symmetric PMM (product maximizing mechanism) • Examples: 1 -step protocol, monotonic concession protocol… EEL 5708

The Monotonic Concession Protocol Rules of this protocol are as follows… • Negotiation proceeds in rounds • On round 1, agents simultaneously propose a deal from the negotiation set • Agreement is reached if one agent finds that the deal proposed by the other is at least as good or better than its proposal • If no agreement is reached, then negotiation proceeds to another round of simultaneous proposals • In round u + 1, no agent is allowed to make a proposal that is less preferred by the other agent than the deal it proposed at time u • If neither agent makes a concession in some round u > 0, then negotiation terminates, with the conflict deal EEL 5708

The Zeuthen Strategy Three problems: • What should an agent’s first proposal be? Its most preferred deal • On any given round, who should concede? The agent least willing to risk conflict • If an agent concedes, then how much should it concede? Just enough to change the balance of risk EEL 5708

Willingness to Risk Conflict • Suppose you have conceded a lot. Then: – Your proposal is now near the conflict deal – In case conflict occurs, you are not much worse off – You are more willing to risk confict • An agent will be more willing to risk conflict if the difference in utility between its current proposal and the conflict deal is low EEL 5708

Nash Equilibrium Again… • The Zeuthen strategy is in Nash equilibrium: under the assumption that one agent is using the strategy the other can do no better than use it himself… • This is of particular interest to the designer of automated agents. It does away with any need for secrecy on the part of the programmer. An agent’s strategy can be publicly known, and no other agent designer can exploit the information by choosing a different strategy. In fact, it is desirable that the strategy be known, to avoid inadvertent conflicts. EEL 5708

Building Blocks ü Domain – A precise definition of what a goal is – Agent operations ü Negotiation Protocol – A definition of a deal – A definition of utility – A definition of the conflict deal • Negotiation Strategy – In Equilibrium – Incentive-compatible EEL 5708

Deception in TODs • Deception can benefit agents in two ways: – Phantom and Decoy tasks Pretending that you have been allocated tasks you have not – Hidden tasks Pretending not to have been allocated tasks that you have been EEL 5708

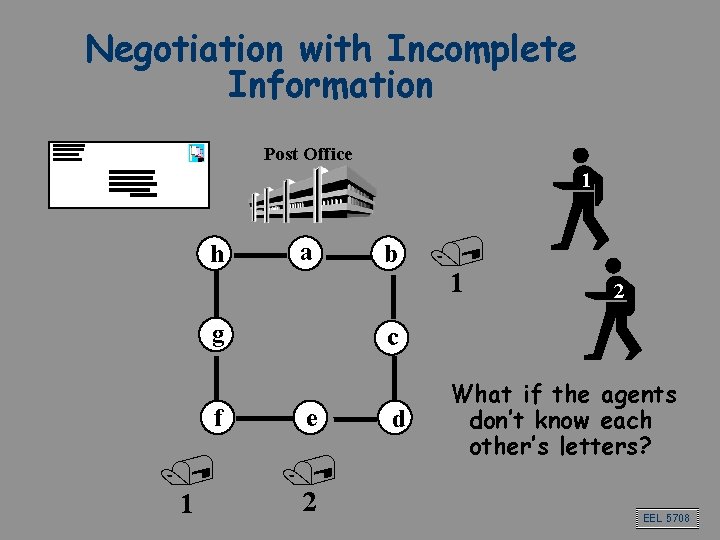
Negotiation with Incomplete Information Post Office 1 h a g f / 1 b / 1 2 c e / 2 d What if the agents don’t know each other’s letters? EEL 5708

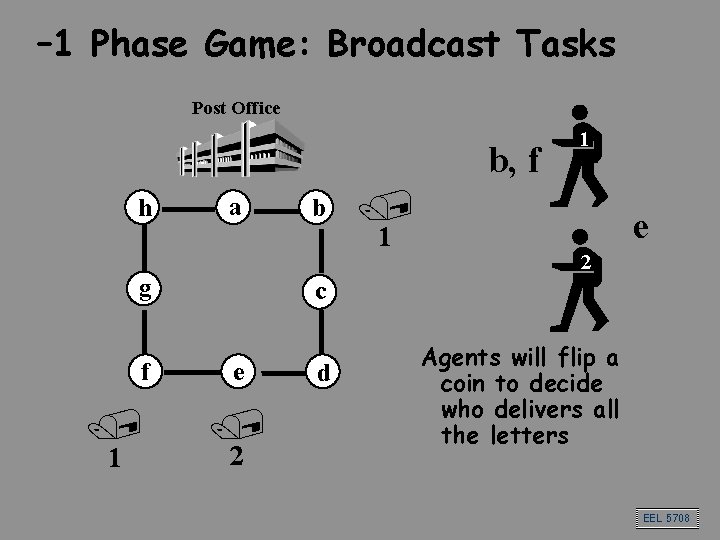
– 1 Phase Game: Broadcast Tasks Post Office b, f h a g f / 1 b 1 / 1 e 2 c e / 2 d Agents will flip a coin to decide who delivers all the letters EEL 5708

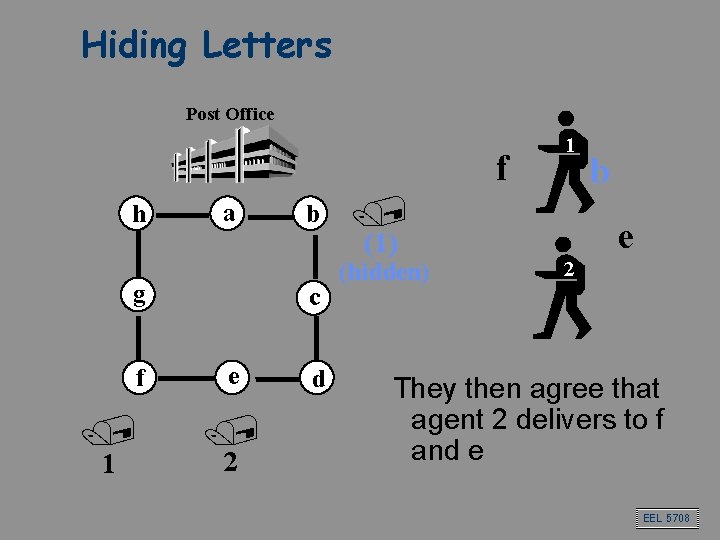
Hiding Letters Post Office h a g f / 1 b c e / 2 d / (1) (hidden) f 1 b e 2 They then agree that agent 2 delivers to f and e EEL 5708

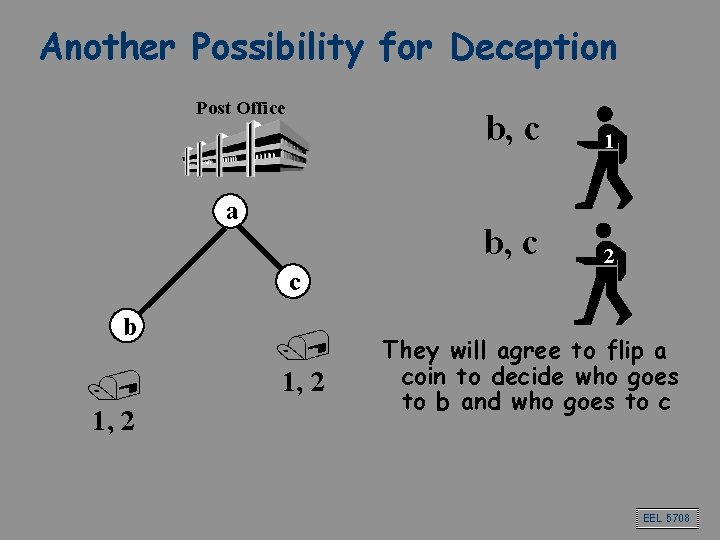
Another Possibility for Deception Post Office a b, c 1 b, c 2 c b / 1, 2 They will agree to flip a coin to decide who goes to b and who goes to c EEL 5708

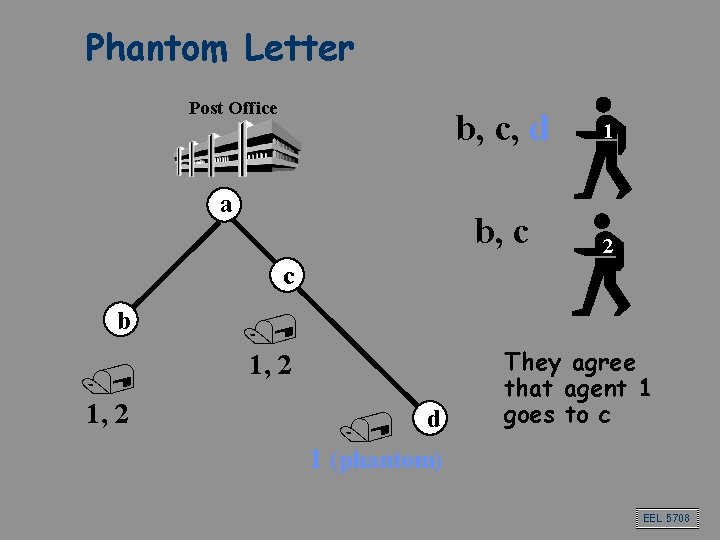
Phantom Letter Post Office a b, c, d 1 b, c 2 c b / 1, 2 / d They agree that agent 1 goes to c 1 (phantom) EEL 5708

Negotiation over Mixed Deals Mixed deal <D 1, D 2> : p The agents will perform <D 1, D 2> with probability p, and the symmetric deal <D 2, D 1> with probability 1 – p Theorem: With mixed deals, agents can always agree on the “all-ornothing” deal – where D 1 is T 1 È T 2 and D 2 is the empty set EEL 5708

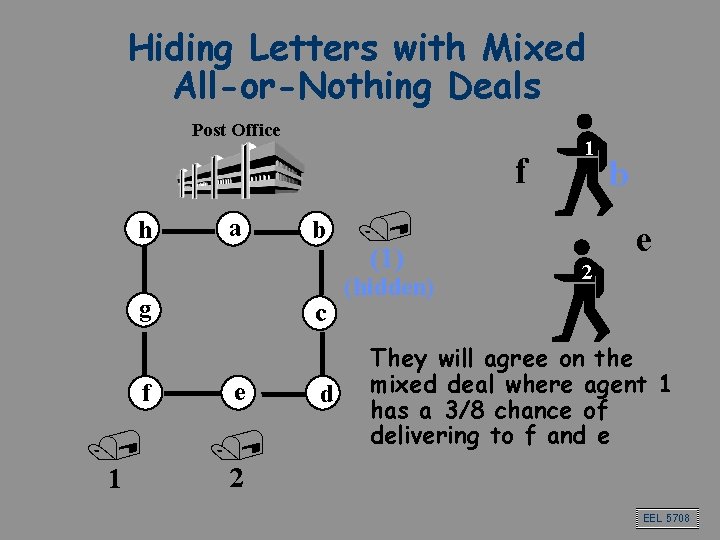
Hiding Letters with Mixed All-or-Nothing Deals Post Office f h a g f / 1 b c e / d 1 / (1) (hidden) b e 2 They will agree on the mixed deal where agent 1 has a 3/8 chance of delivering to f and e 2 EEL 5708

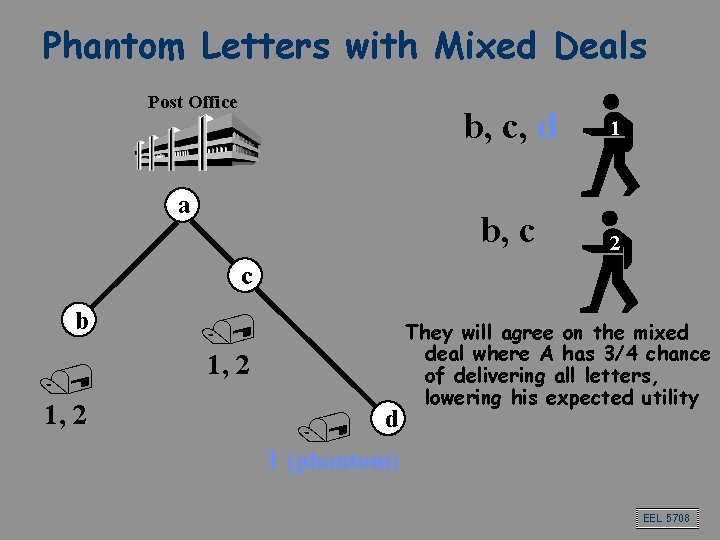
Phantom Letters with Mixed Deals Post Office a b, c, d 1 b, c 2 c b / 1, 2 / d They will agree on the mixed deal where A has 3/4 chance of delivering all letters, lowering his expected utility 1 (phantom) EEL 5708

Sub-Additive TODs TOD < T, Ag, c > is sub-additive if for all finite sets of tasks X, Y in T we have: c(X È Y) £ c(X) + c(Y) EEL 5708

Sub-Additivity X Y c(X È Y) £ c(X) + c(Y) EEL 5708

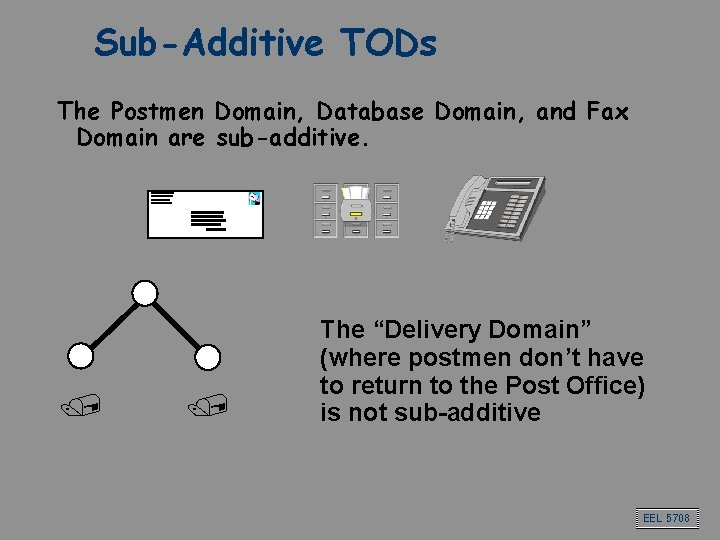
Sub-Additive TODs The Postmen Domain, Database Domain, and Fax Domain are sub-additive. / / The “Delivery Domain” (where postmen don’t have to return to the Post Office) is not sub-additive EEL 5708

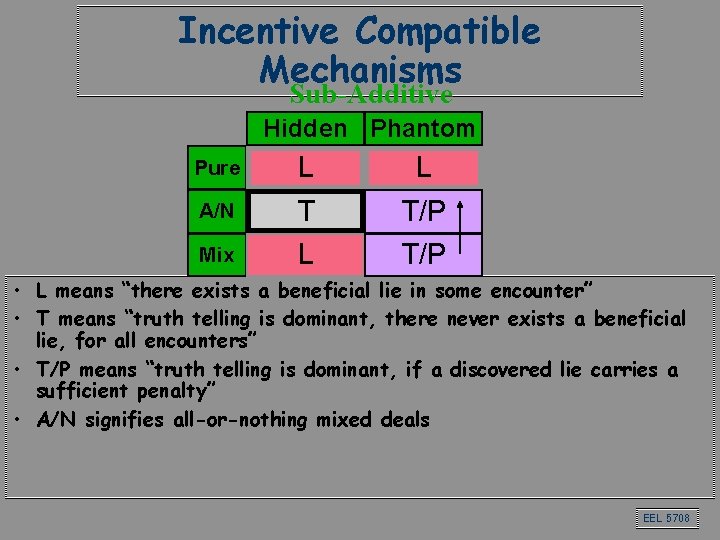
Incentive Compatible Mechanisms Sub-Additive Hidden Phantom A/N L T Mix L Pure L T/P • L means “there exists a beneficial lie in some encounter” • T means “truth telling is dominant, there never exists a beneficial lie, for all encounters” • T/P means “truth telling is dominant, if a discovered lie carries a sufficient penalty” • A/N signifies all-or-nothing mixed deals EEL 5708

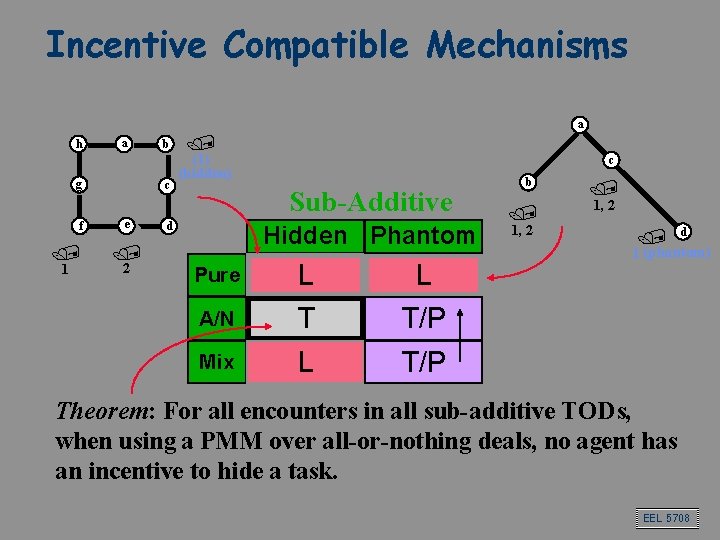
Incentive Compatible Mechanisms a h a g f / 1 b c e / 2 / (1) (hidden) c Sub-Additive d Hidden Phantom A/N L T Mix L Pure L b / 1, 2 / d 1 (phantom) T/P Theorem: For all encounters in all sub-additive TODs, when using a PMM over all-or-nothing deals, no agent has an incentive to hide a task. EEL 5708

Incentive Compatible Mechanisms Hidden Phantom A/N L T Mix L Pure L T/P • Explanation of the up-arrow: If it is never beneficial in a mixed deal encounter to use a phantom lie (with penalties), then it is certainly never beneficial to do so in an all-or-nothing mixed deal encounter (which is just a subset of the mixed deal encounters) EEL 5708

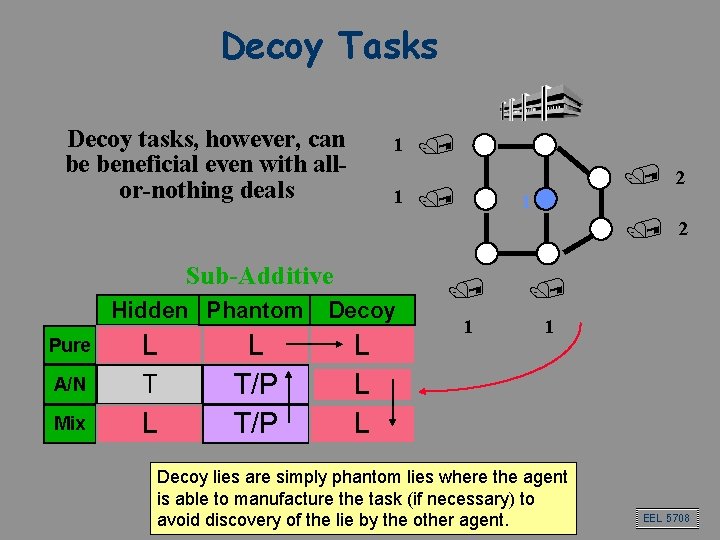
Decoy Tasks Decoy tasks, however, can be beneficial even with allor-nothing deals 1 1 Sub-Additive Hidden Phantom Pure L A/N T Mix L L T/P Decoy L L L / / / 2 1 / / 1 1 Decoy lies are simply phantom lies where the agent is able to manufacture the task (if necessary) to avoid discovery of the lie by the other agent. EEL 5708

Decoy Tasks Sub-Additive Hidden Phantom Pure L A/N T Mix L L T/P Decoy L L L • Explanation of the down arrow: If there exists a beneficial decoy lie in some all-or-nothing mixed deal encounter, then there certainly exists a beneficial decoy lie in some general mixed deal encounter (since all-ornothing mixed deals are just a subset of general mixed deals) EEL 5708

Decoy Tasks Sub-Additive Hidden Phantom Pure L A/N T Mix L L T/P Decoy L L L • Explanation of the horizontal arrow: If there exists a beneficial phantom lie in some pure deal encounter, then there certainly exists a beneficial decoy lie in some pure deal encounter (since decoy lies are simply phantom lies where the agent is able to manufacture the task if necessary) EEL 5708

Concave TODs TOD < T, Ag, c > is concave if for all finite sets of tasks Y and Z in T , and X Í Y, we have: c(Y È Z) – c(Y) £ c(X È Z) – c(X) Concavity implies sub-additivity EEL 5708

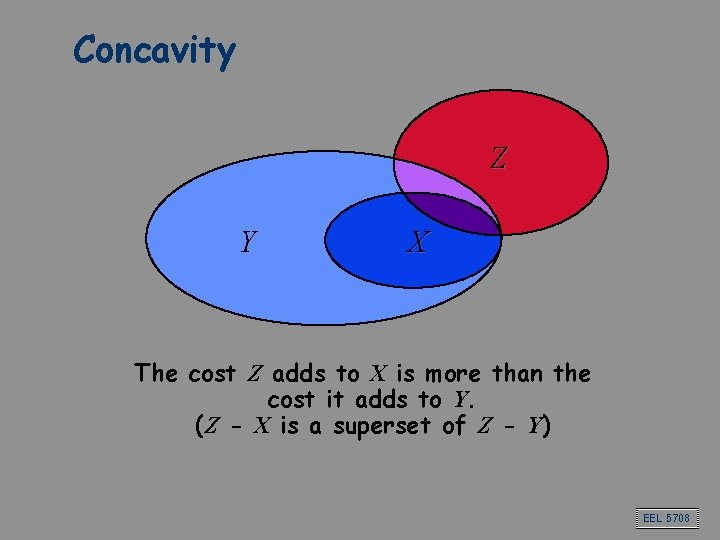
Concavity Z Y X The cost Z adds to X is more than the cost it adds to Y. (Z - X is a superset of Z - Y) EEL 5708

Concave TODs The Database Domain and Fax Domain are concave (not the Postmen Domain, unless restricted to trees). Z 1/ X 1/ / 2 1 /2 / / 1 1 This example was not concave; Z adds 0 to X, but adds 2 to its superset Y (all blue nodes) EEL 5708

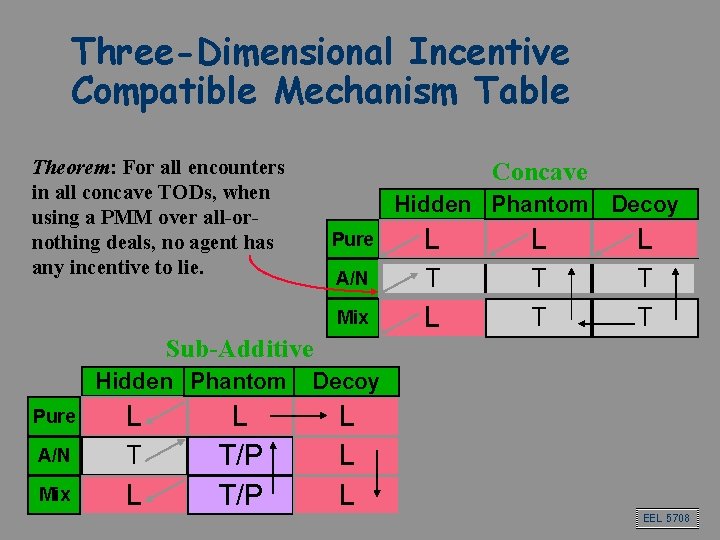
Three-Dimensional Incentive Compatible Mechanism Table Theorem: For all encounters in all concave TODs, when using a PMM over all-ornothing deals, no agent has any incentive to lie. Concave Hidden Phantom Decoy Pure L L L A/N T T T Mix L T T Sub-Additive Hidden Phantom Pure L A/N T Mix L L T/P Decoy L L L EEL 5708

Modular TODs TOD < T, Ag, c > is modular if for all finite sets of tasks X, Y in T we have: c(X È Y) = c(X) + c(Y) – c(X Ç Y) Modularity implies concavity EEL 5708

Modularity X Y c(X È Y) = c(X) + c(Y) – c(X Ç Y) EEL 5708

Modular TODs The Fax Domain is modular (not the Database Domain nor the Postmen Domain, unless restricted to a star topology). Even in modular TODs, hiding tasks can be beneficial in general mixed deals EEL 5708

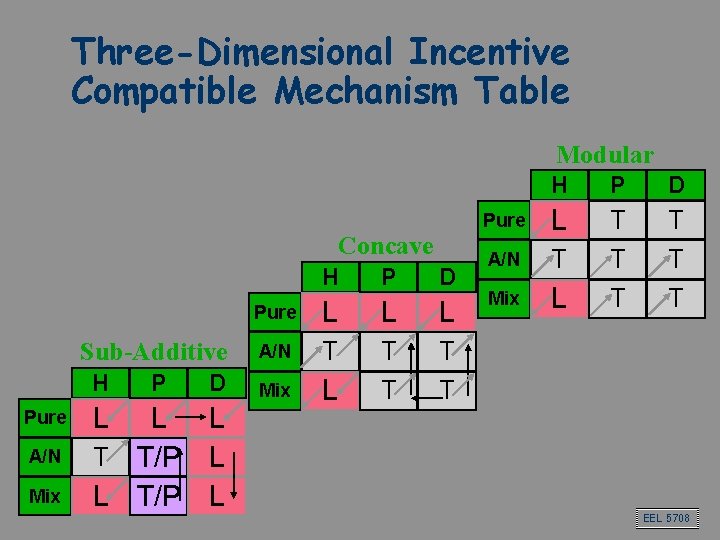
Three-Dimensional Incentive Compatible Mechanism Table Modular Concave Sub-Additive H Pure A/N Mix L P D L L T T/P L L T/P L H P D Pure L L L A/N T T T Mix L T T H P D Pure L T T A/N T T T Mix L T T EEL 5708

Related Work • Similar analysis made of State Oriented Domains, where situation is more complicated • Coalitions (more than two agents, Kraus, Shechory) • Mechanism design (Sandholm, Nisan, Tennenholtz, Ephrati, Kraus) • Other models of negotiation (Kraus, Sycara, Durfee, Lesser, Gasser, Gmytrasiewicz) • Consensus mechanisms, voting techniques, economic models (Wellman, Ephrati) EEL 5708

Conclusions • By appropriately adjusting the rules of encounter by which agents must interact, we can influence the private strategies that designers build into their machines • The interaction mechanism should ensure the efficiency of multi-agent systems Rules of Encounter Efficiency EEL 5708

Conclusions • To maintain efficiency over time of dynamic multi-agent systems, the rules must also be stable • The use of formal tools enables the design of efficient and stable mechanisms, and the precise characterization of their properties Stability Formal Tools EEL 5708

• • Argumentation is the process of attempting to convince others of something Gilbert (1994) identified 4 modes of argument: 1. 2. 3. 4. Logical mode “If you accept that A and that A implies B, then you must accept that B” Emotional mode “How would you feel if it happened to you? ” Visceral mode “Cretin!” Kisceral mode “This is against Christian teaching!” EEL 5708

Logic-based Argumentation Basic form of logical arguments is as follows: Database | (Sentence, Grounds) where: • Database is a (possibly inconsistent) set of logical formulae • Sentence is a logical formula known as the conclusion • Grounds is a set of logical formulae such that: 1. Grounds f Database; and 2. Sentence can be proved from Grounds EEL 5708

Attack and Defeat • Let (f 1, G 1) and (f 2, G 2) be arguments from some database D… Then (f 2, G 2) can be defeated (attacked) in one of two ways: • (f 1, G 1) rebuts (f 2, G 2) if f 1 / f 2 • (f 1, G 1) undercuts (f 2, G 2) if f 1 / y 2 for some y 0 G 2 A rebuttal or undercut is known as an attack EEL 5708

Abstract Argumentation • Concerned with the overall structure of the argument (rather than internals of arguments) • Write x y – “argument x attacks argument y” – “x is a counterexample of y” – “x is an attacker of y” where we are not actually concerned as to what x, y are • An abstract argument system is a collection or arguments together with a relation “ ” saying what attacks what • An argument is out if it has an undefeated attacker, and in if all its attackers are defeated EEL 5708

An Example Abstract Argument System EEL 5708