Comparisons of Measurements and Gyrokinetic Simulations of Turbulence

Comparisons of Measurements and Gyrokinetic Simulations of Turbulence and Transport in Alcator C-Mod EDA H-Mode Discharges M. B. Sampsell, R. V. Bravenec Fusion Research Center, The University of Texas at Austin J. Candy General Atomics D. R. Ernst, Alcator C-Mod Team Plasma Science and Fusion Center, MIT W. M. Nevins Lawrence Livermore National Laboratory

Motivation u Beam-emission spectroscopy (BES) has detected the “quasi-coherent mode” at the edge of enhanced D (EDA) H-mode plasmas. u However, it has not detected any broadband fluctuations at the top of the H-mode pedestal. Why? u No localized fluctuation measurements exist by any diagnostic. Approach: u Calculate the turbulence from a nonlinear gyrokinetic code (GYRO*). u Model the diagnostic and apply it to the computation results (“synthetic diagnostic”) * J. Candy, J. Comput. Phys. 186, 545 (2003).

C-Mod EDA Profiles EDA (enhanced D ) H-mode discharge at start of ITB u Radius of interest: R 0. 87 m, where density profile is very flat (if not inverted).

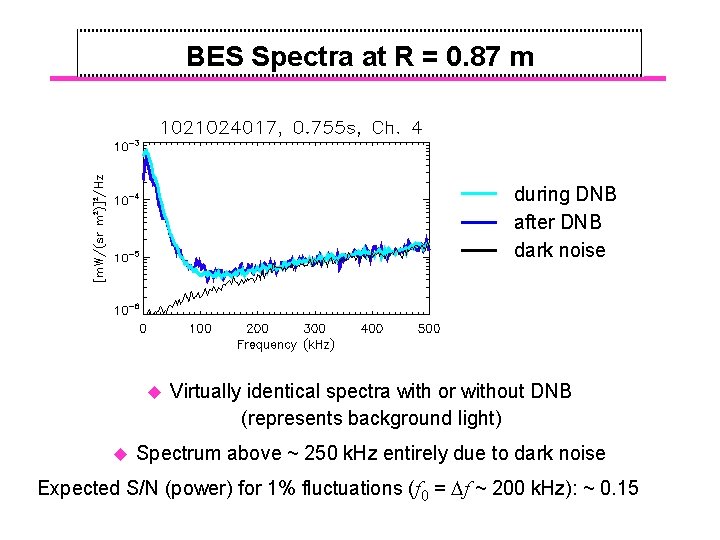
BES Spectra at R = 0. 87 m during DNB after DNB dark noise u u Virtually identical spectra with or without DNB (represents background light) Spectrum above ~ 250 k. Hz entirely due to dark noise Expected S/N (power) for 1% fluctuations (f 0 = f ~ 200 k. Hz): ~ 0. 15

GYRO Simulation u r 0 = 0. 825 a = 0. 192 m (ne 0 2 x 1020 m-3, Te 0 0. 540 ke. V, BT = 5. 5 T) u 16 toroidal modes n = 0 – 120 (k s = 0 – 0. 815) u Kinetic electrons u Periodic boundary conditions (no background E B shear) u 115 s x 115 s simulation domain, 128 radial grid points u One impurity: Boron u Length of run: 867 a/cs 1. 17 ms u Other parameters: = 0. 825 q = 3. 95 = 2. 70 R/a = 3. 07 = 1. 40 = 0. 28 = – 0. 12 Ti/Te = 0. 92 Lni/a = 200 LTi/a = 0. 23 LTe/a = 0. 37 * = 0. 0015 Zeff = 1. 61 ei = 1. 2 s

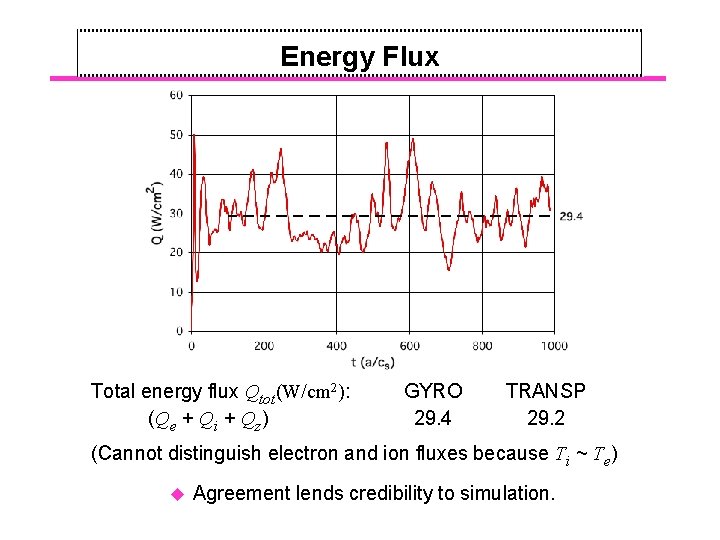
Energy Flux Total energy flux Qtot(W/cm 2): (Qe + Qi + Qz) GYRO 29. 4 TRANSP 29. 2 (Cannot distinguish electron and ion fluxes because Ti ~ Te) u Agreement lends credibility to simulation.

Spatial Density Fluctuation Distribution u Scale size 1 cm in nonlinear phase u Average “downward” propagation (electron diamagnetic direction) This and subsequent analysis performed using GKV (W. M. Nevins, LLNL Rept. UCRLTR-206016, August, 2004).

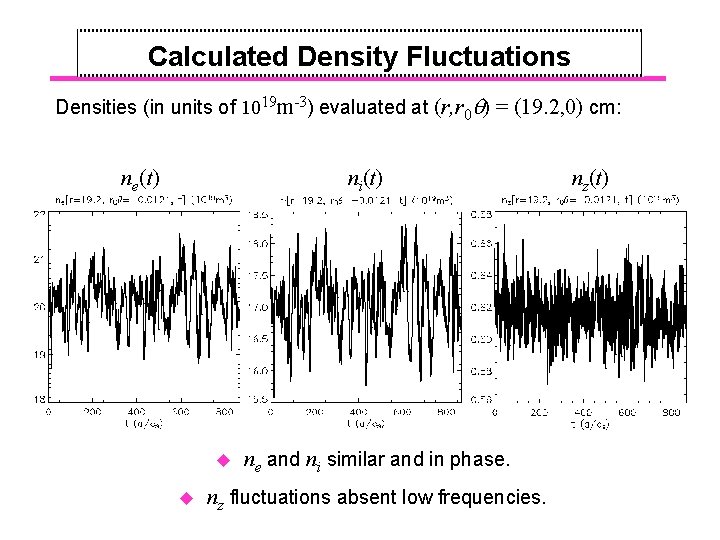
Calculated Density Fluctuations Densities (in units of 1019 m-3) evaluated at (r, r 0 ) = (19. 2, 0) cm: ne(t) ni(t) u u ne and ni similar and in phase. nz fluctuations absent low frequencies. nz(t)

Signal Fluctuations BES detects Doppler-shifted H emission from a neutral beam, which is a function of beam energy, impurity charge, and electron and ion densities. 1, 2 There are two diagnostic “filters”: u The emissivity rate ne v as a function of the densities. u The diagnostic’s spatial sensitivity function which averages over any fine structure. 1 W. M. Mandl, et al. , “Beam emission spectroscopy as a comprehensive plasma diagnostic tool, ” Plasma Phys. Control. Fusion 35 1373 (1993). 2 I. H. Hutchinson, ” Excited-state populations in neutral beam emission, ” Plasma Phys. Control. Fusion 44 71 (2002).

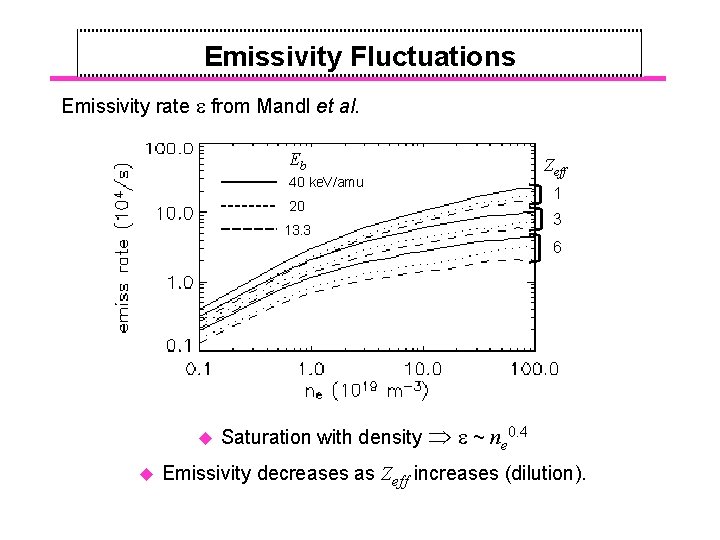
Emissivity Fluctuations Emissivity rate e from Mandl et al. Eb 40 ke. V/amu 20 13. 3 Zeff 1 3 6 u u Saturation with density e ~ ne 0. 4 Emissivity decreases as Zeff increases (dilution).

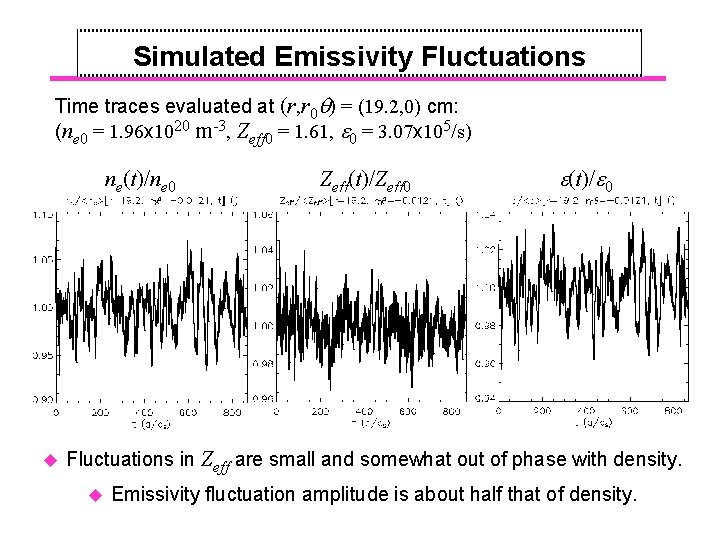
Simulated Emissivity Fluctuations Time traces evaluated at (r, r 0 ) = (19. 2, 0) cm: (ne 0 = 1. 96 x 1020 m-3, Zeff 0 = 1. 61, 0 = 3. 07 x 105/s) ne(t)/ne 0 u Zeff(t)/Zeff 0 (t)/ 0 Fluctuations in Zeff are small and somewhat out of phase with density. u Emissivity fluctuation amplitude is about half that of density.

BES Spatial Sensitivity Function f(x, y) = f 0 exp(-[(x-x 0)/dx]px) exp(-[(y-y 0)/dx]py) x 0 = 19. 2, y 0 = 0, dx = 0. 8, dy = 0. 5, px = 4, py = 6

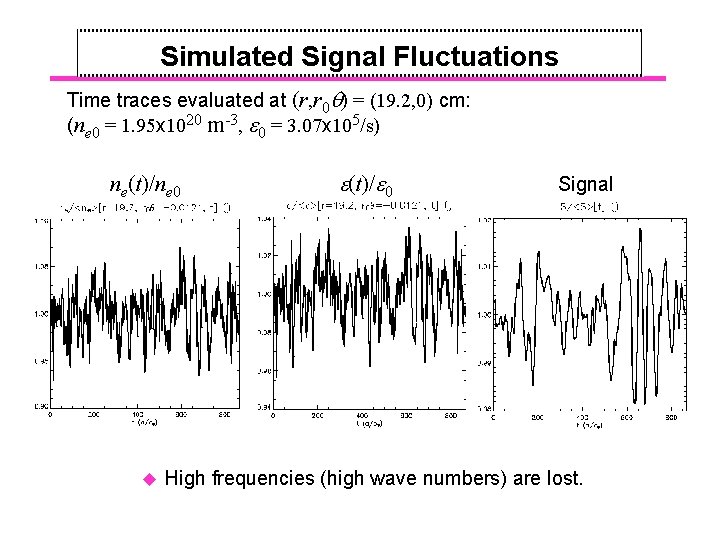
Simulated Signal Fluctuations Time traces evaluated at (r, r 0 ) = (19. 2, 0) cm: (ne 0 = 1. 95 x 1020 m-3, 0 = 3. 07 x 105/s) ne(t)/ne 0 u (t)/ 0 Signal High frequencies (high wave numbers) are lost.

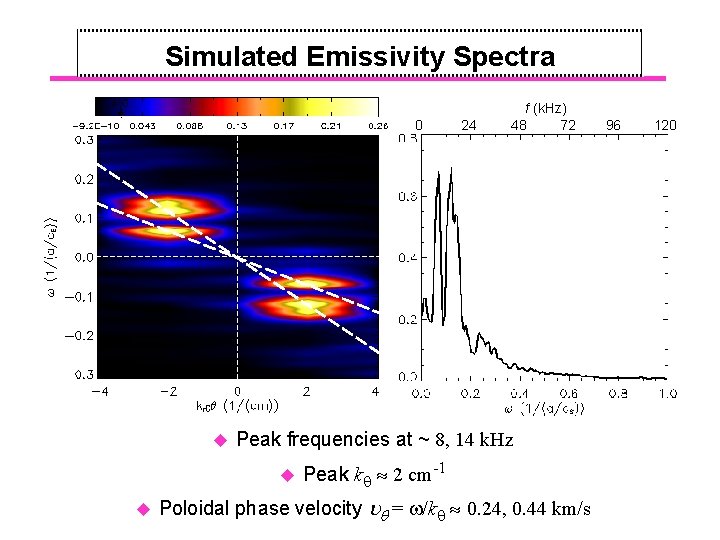
Simulated Emissivity Spectra 0 u Peak frequencies at ~ 8, 14 k. Hz u u 24 f (k. Hz) 48 72 Peak k 2 cm-1 Poloidal phase velocity = /k 0. 24, 0. 44 km/s 96 120

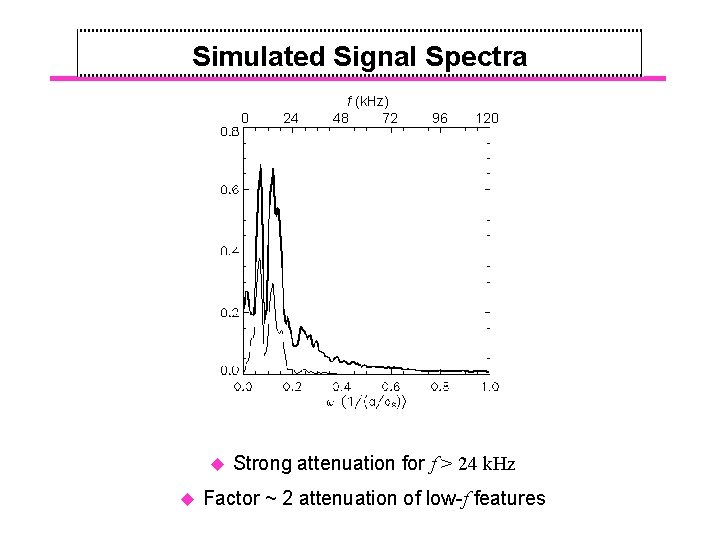
Simulated Signal Spectra 0 u u 24 f (k. Hz) 48 72 96 120 Strong attenuation for f > 24 k. Hz Factor ~ 2 attenuation of low-f features

Summary u GYRO simulation of top of EDA H-mode pedestal predicts correct total energy flux. u H emissivity fluctuations from DNB are about half density fluctuations. u Higher frequencies (> 25 k. Hz) in BES signal strongly attenuated by finite collection area, in apparent agreement with data.

Future Work u Factor ~2 reduction of measured fluctuations from density fluctuations a given. Reduce BES collection area: two 1 -mm optical fibers per channel instead of four Caveats: u F Will reduce signals by factor two. F Ultimate radial spatial resolution (~ 0. 9 cm) determined by optical aberrations and beam smearing. Decrease spacing between channels: Go to 6 x 6 densely packed fiber array rather than discrete four-fiber bundles separated by ~ 1 cm.