Comparison of the energy levels of an infinite

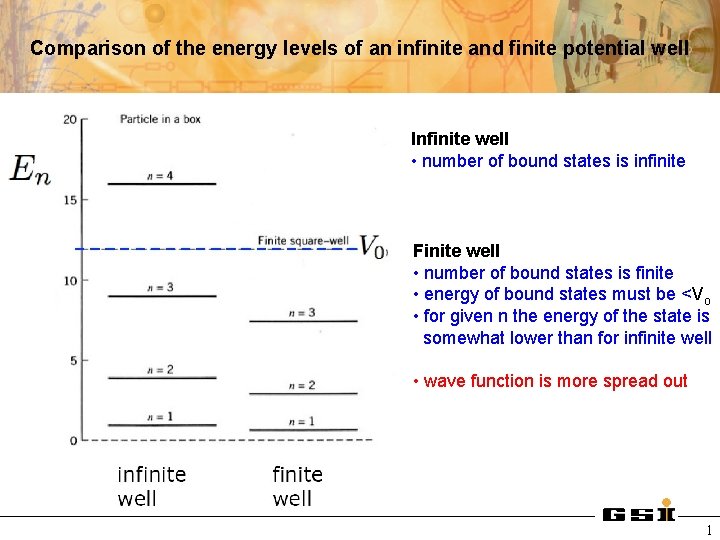
Comparison of the energy levels of an infinite and finite potential well Infinite well • number of bound states is infinite Finite well • number of bound states is finite • energy of bound states must be <Vo • for given n the energy of the state is somewhat lower than for infinite well • wave function is more spread out 1

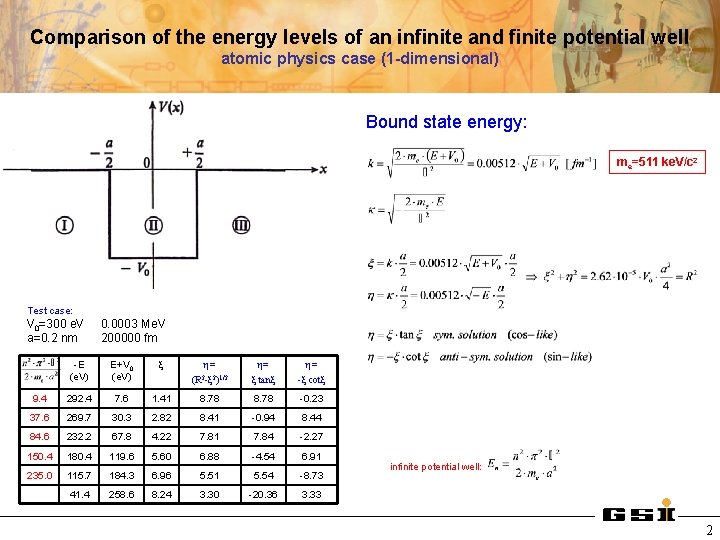
Comparison of the energy levels of an infinite and finite potential well atomic physics case (1 -dimensional) Bound state energy: me=511 ke. V/c 2 Test case: V 0=300 e. V a=0. 2 nm 0. 0003 Me. V 200000 fm -E (e. V) E+V 0 (e. V) ξ η= (R 2 -ξ 2)1/2 η= ξ tanξ η= -ξ cotξ 9. 4 292. 4 7. 6 1. 41 8. 78 -0. 23 37. 6 269. 7 30. 3 2. 82 8. 41 -0. 94 8. 44 84. 6 232. 2 67. 8 4. 22 7. 81 7. 84 -2. 27 150. 4 180. 4 119. 6 5. 60 6. 88 -4. 54 6. 91 235. 0 115. 7 184. 3 6. 96 5. 51 5. 54 -8. 73 41. 4 258. 6 8. 24 3. 30 -20. 36 3. 33 infinite potential well: 2

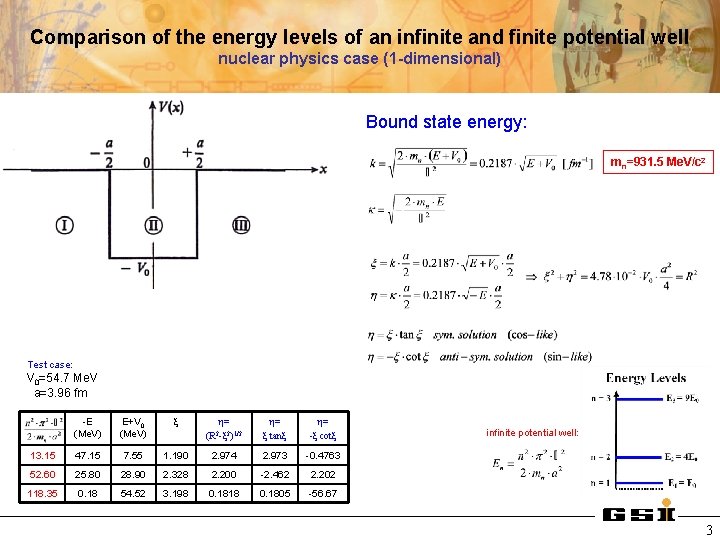
Comparison of the energy levels of an infinite and finite potential well nuclear physics case (1 -dimensional) Bound state energy: mn=931. 5 Me. V/c 2 Test case: V 0=54. 7 Me. V a=3. 96 fm -E (Me. V) E+V 0 (Me. V) ξ 13. 15 47. 15 7. 55 52. 60 25. 80 118. 35 0. 18 η= (R 2 -ξ 2)1/2 η= ξ tanξ η= -ξ cotξ 1. 190 2. 974 2. 973 -0. 4763 28. 90 2. 328 2. 200 -2. 462 2. 202 54. 52 3. 198 0. 1818 0. 1805 -56. 67 infinite potential well: 3

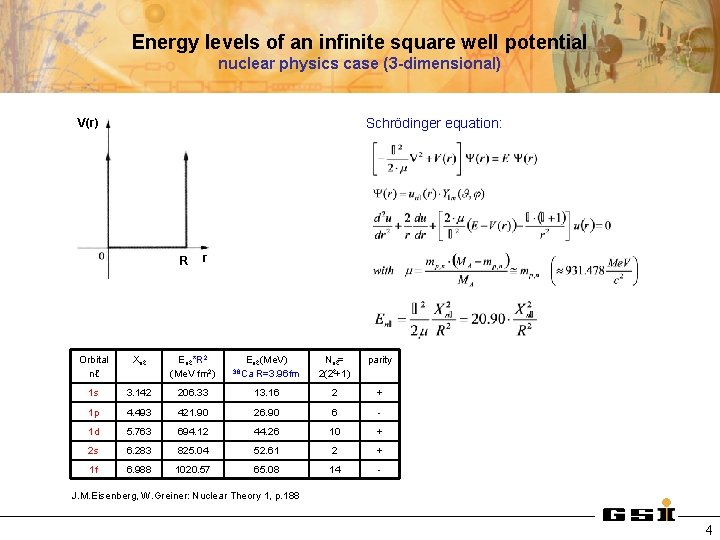
Energy levels of an infinite square well potential nuclear physics case (3 -dimensional) V(r) Schrödinger equation: R r Orbital nℓ Xnℓ Enℓ *R 2 (Me. V fm 2) Enℓ (Me. V) 36 Ca R=3. 96 fm Nnℓ= 2(2ℓ+1) parity 1 s 3. 142 206. 33 13. 16 2 + 1 p 4. 493 421. 90 26. 90 6 - 1 d 5. 763 694. 12 44. 26 10 + 2 s 6. 283 825. 04 52. 61 2 + 1 f 6. 988 1020. 57 65. 08 14 - J. M. Eisenberg, W. Greiner: Nuclear Theory 1, p. 188 4

Comparison of the energy levels of an infinite and finite potential well nuclear physics case: 36 Ca, 36 S (3 -dimensional) ℓ=0 energies: ℓ=1 energies: ℓ=2 energies: Orbital nℓ Enℓ (Me. V) 36 Ca R=3. 96 fm Enℓ (Me. V) V 0=54. 7 Me. V 1 s 13. 16 9. 75 9. 55 1 p 26. 90 19. 77 19. 31 1 d 44. 26 32. 20 31. 32 2 s 52. 61 37. 55 36. 25 1 f 65. 08 36 Ca 36 S Enℓ (Me. V) V 0=47. 3 Me. V 5

Depth of the potential square well deuteron case (3 -dimensional) ℓ=0 energies: 6

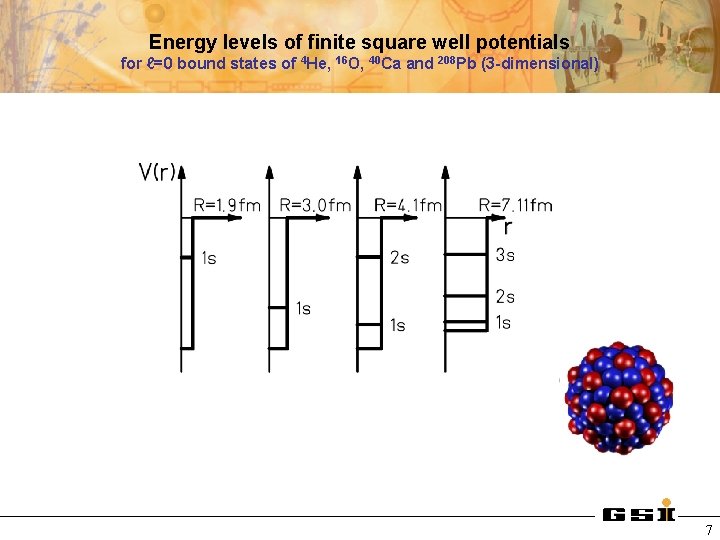
Energy levels of finite square well potentials for ℓ=0 bound states of 4 He, 16 O, 40 Ca and 208 Pb (3 -dimensional) 7

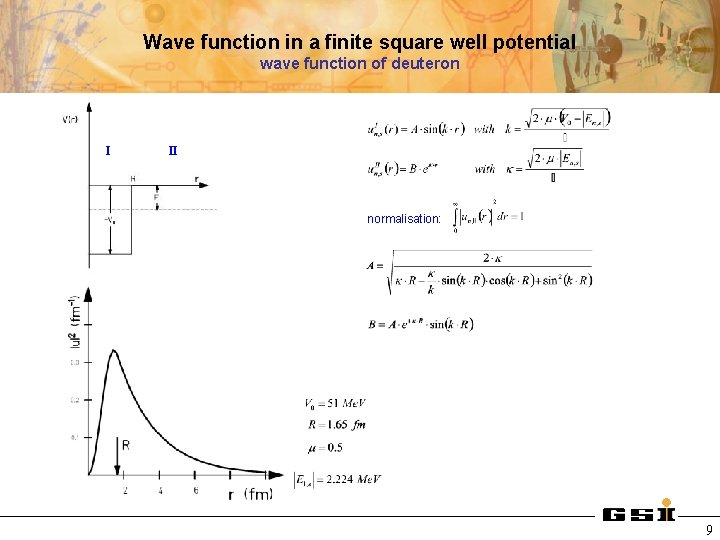
Wave function in a finite square well potential wave function of deuteron Ι ΙΙ normalisation: 9

Mean square radius – a measure of the nuclear size outer region inner region 10