Comparison of frequentist and Bayesian regularization in structural

Comparison of frequentist and Bayesian regularization in structural equation modeling. Ross Jacobucci, Kevin Grimm, & John J. Mc. Ardle IMPS 2016 – Asheville, NC

Overview • Regularization has become a popular tool in regression and graphical modeling for a number of reasons: • • Produces sparse solutions Can overcome collinearity P > N; Estimable and more efficient with large P Increased generalizability • Slight increase in bias for larger decrease in variance • Despite this, it has seen little application in psychometrics outside of sparse PCA or EFA • Although three recent applications to SEM: • Regularized Structural Equation Modeling (Jacobucci, Grimm, & Mc. Ardle, 2016) • Bayesian Factor Analysis with Spike-and-Slab Prior (Lu, Chow, & Loken, 2016) • Penalized Network Models (Epskamp, Rhemtulla, & Borsboom, Under Review)

Regularized Structural Equation Modeling (Reg. SEM) •

Bayesian SEM and Regularization • Bayesian SEM as implemented in Mplus (Muthen & Asparouhov; 2012) • Use of small variance priors on non-target parameters • Equivalent to the use of ridge penalties in frequentist framework • Only possible to use Normal distribution priors for factor loadings • Bayesian factor analysis with spike-and-slab prior • • Lu, Chow, & Loken (2016) “spike” for parameters set to 0 “slab” higher variance normal distribution for non-zero parameters Similar to SEM heuristic search algorithms (i. e. Marcoulides & Ing, 2011) in frequentist framework • BSEM Lasso • Use of the Laplace (double exponential) distribution on target parameters • By decreasing the variance of the prior, will move parameter estimates close to 0 • Shown similarity between Bayes and frequentist lasso in context of regression • E. g. Park & Casella (2008)

Purpose • Show equivalence with Reg. SEM Ridge and Mplus BSEM • To date, no work with Bayesian Lasso in SEM (BSEM Lasso) • As an illustrative example: • Show similarity between Reg. SEM Lasso and BSEM Lasso • Holzinger-Swineford (1939) • How do they compare in choosing “true” loadings of 0? • Small simulation comparing Reg. SEM and BSEM Lasso on choosing factor loadings = 0

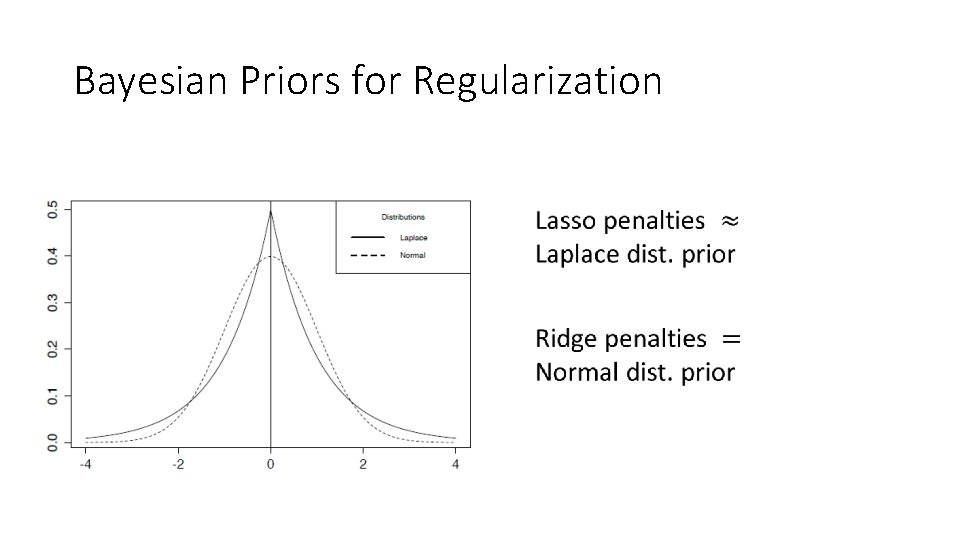
Bayesian Priors for Regularization

Ridge Equivalence • Lu, Chow, & Loken (2016) have already pointed out equivalence of BSEM w/ small variance priors and Ridge regularization • Requires putting small variance normal priors on specific parameters • Can be done in both Mplus and blavaan (JAGS) • Different default priors, but as long as they are noninformative there is close equivalence • Get same estimates and fit across Bayesian and frequentist implementations • Use type=“ridge” in regsem package • Simple Example: • First 6 scales from Holzinger Swineford (1939) dataset in lavaan package

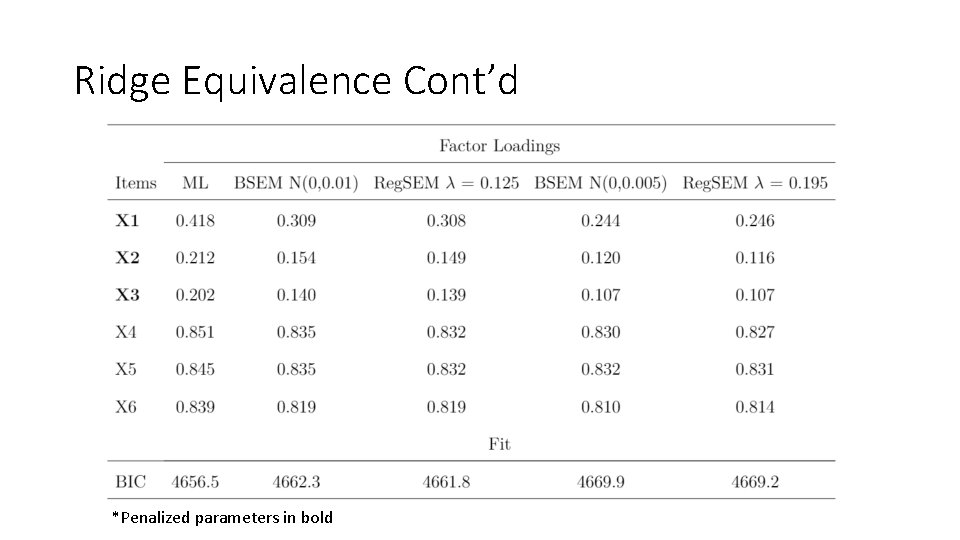
Ridge Equivalence Cont’d *Penalized parameters in bold

Lasso Comparison • One factor model with first 6 scales from Holzinger Swineford (1939) • Penalize all loadings while setting factor variance to 1 • Use cv_regsem function from the regsem package to test 65 penalty values • Bayes SEM Lasso implemented using the blavaan package in R • Uses JAGS in background and generates model scripts • Test 30 different values of precision

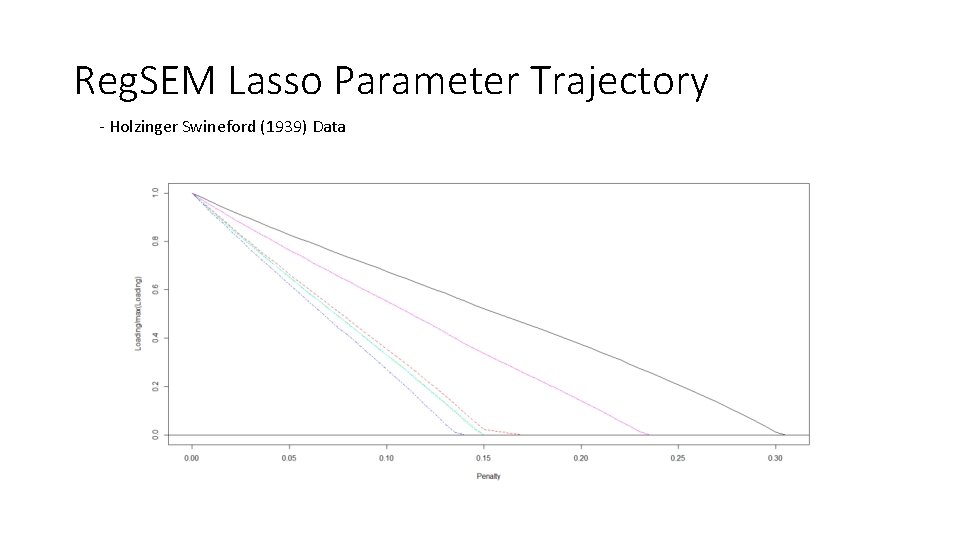
Reg. SEM Lasso Parameter Trajectory - Holzinger Swineford (1939) Data

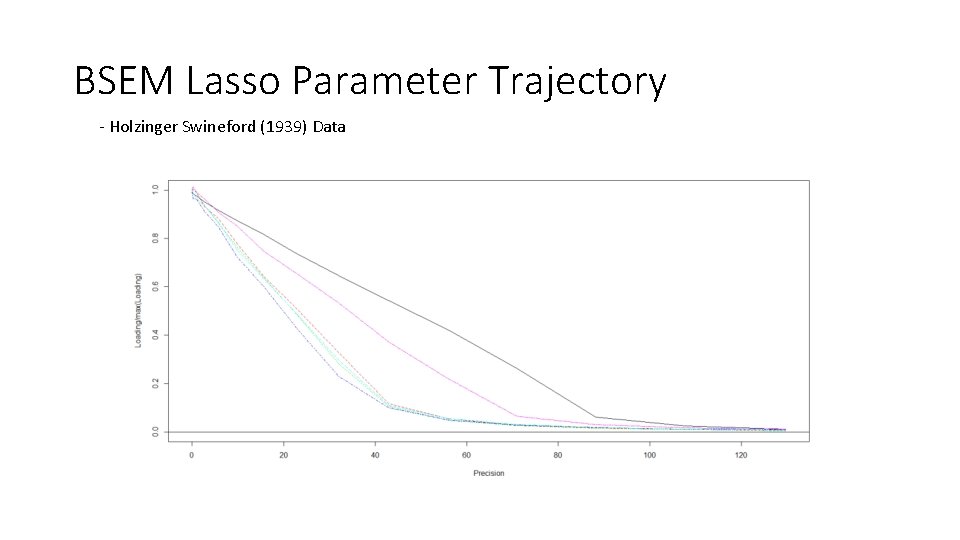
BSEM Lasso Parameter Trajectory - Holzinger Swineford (1939) Data

Simulation • Used simulate. Data() from lavaan • According to factor structure • N = 200 • 2 ways to record accuracy • Simulated loadings of 0 not measured as 0 in final model • Simulated loadings of 0. 2 measured as 0 in final model • Reg. SEM • Just use BIC to choose final model • BSEM Lasso • use posterior mode parameter estimates and whether credible interval includes 0 • BIC, DIC, WAIC, LOOIC, log likelihood and marginal log likelihood from blavaan package • Both methods used 30 -60 variances/penalties

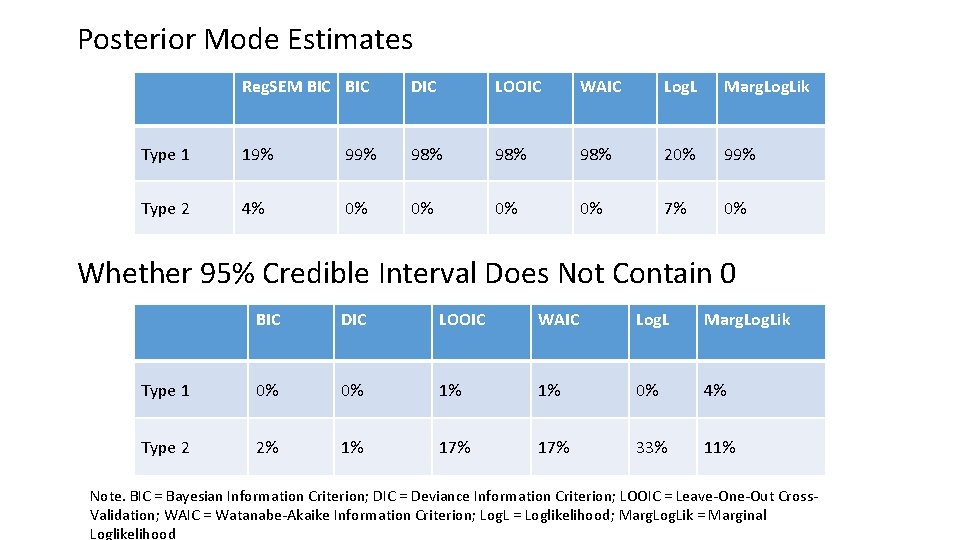
Posterior Mode Estimates Reg. SEM BIC DIC LOOIC WAIC Log. L Marg. Log. Lik Type 1 19% 98% 98% 20% 99% Type 2 4% 0% 0% 7% 0% Whether 95% Credible Interval Does Not Contain 0 BIC DIC LOOIC WAIC Log. L Marg. Log. Lik Type 1 0% 0% 1% 1% 0% 4% Type 2 2% 1% 17% 33% 11% Note. BIC = Bayesian Information Criterion; DIC = Deviance Information Criterion; LOOIC = Leave-One-Out Cross. Validation; WAIC = Watanabe-Akaike Information Criterion; Log. L = Loglikelihood; Marg. Log. Lik = Marginal Loglikelihood

Discussion • Just as in Regression, the BSEM Lasso seems to be a hybrid between frequentist Ridge and Lasso • Rarely will estimate posterior modes as close to 0 • However, using credible interval is highly accurate in determining “true” zero loadings • Didn’t compare to noninformative prior or Normal (Ridge) priors • Similar run times • Convergence slower for both methods when penalty/prior becomes more restrictive • However, every BSEM Lasso model converged • Advantage of BSEM Lasso is that standard errors are available • Both methods available in open-source software • Spike and Slab prior for SEM is not yet

Future Directions • Model Identification needs guidelines • Use of informative priors allows for fitting models that wouldn’t otherwise be identified • Same with use of penalties in Reg. SEM • Prior variance selection in BSEM • No guidelines • Standard errors in Reg. SEM • Not a problem in Ridge or Lasso BSEM • Worth investigating hierarchical Lasso priors for BSEM • Eliminates need to test multiple prior variances

Acknowledgements • Thanks to Ed Merkle for help in tailoring the blavaan package to the analyses used in this presentation • Ross Jacobucci was supported by funding through the National Institute on Aging Grant Number T 32 AG 0037.

References • Epskamp, S. , Rhemtulla, M. , & Borsboom, M. (Under Review). Generalized Network Psychometrics: Combining Network and Latent Variable Models. Psychometrika. Downloaded from first authors Researchgate • Jacobucci, R. , Grimm, K. J. , & Mc. Ardle, J. J. (2016). Regularized Structural Equation Modeling: A Multidisciplinary Journal, 23(4), 555 -566. • Lu, Z. H. , Chow, S. M. , & Loken, E. (2016). Bayesian factor analysis as a variable-selection problem: Alternative priors and consequences, 1 -21, doi: 10. 1080/00273171. 2016. 1168279 • Muthén, B. O. , & Asparouhov, T. (2012). Bayesian structural equation modeling: A more flexible representation of substantive theory. Psychological Methods, 17, 313– 335. doi: 10. 1037/a 0026802