Comparison of Fiber Reference and Zernike Filter Self

Comparison of Fiber Reference and Zernike Filter Self Referencing Interferometers Kavita Chand, M. S. , M. Tech, and Justin Mansell, Ph. D. MZA Associates Corporation Troy Rhoadarmer Air Force Research Laboratory Kirtland AFB, Albuquerque, NM 1

Introduction • Self-referencing interferometers (SRIs) have been proposed to provide feedback for adaptive optics systems in directed energy applications. • We performed wave-optics analysis in Wave. Train to compare two types of SRI: – Fiber-reference SRIs and – Zernike filter SRIs. 2
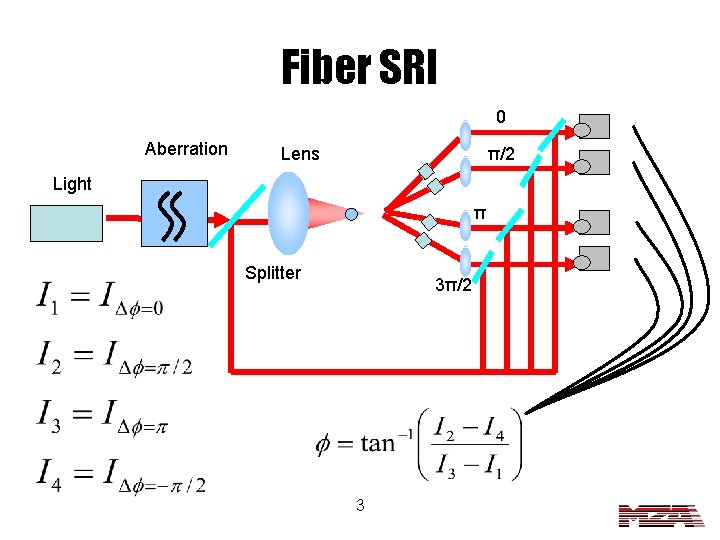
Fiber SRI 0 Aberration Lens π/2 Light π Splitter 3π/2 3
Wave. Train Fiber. SRI 4
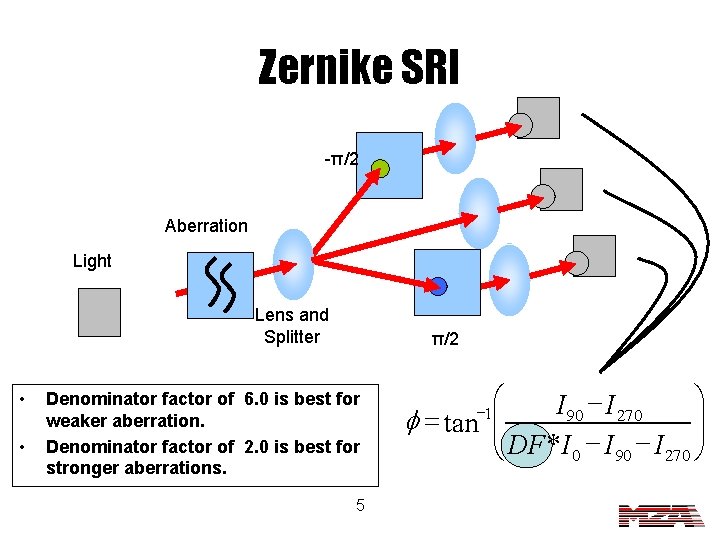
Zernike SRI -π/2 Aberration Light Lens and Splitter • • π/2 Denominator factor of 6. 0 is best for weaker aberration. Denominator factor of 2. 0 is best for stronger aberrations. 5 æ ö - I 270 I 90 ÷÷ f = tan çç è DF * I 0 - I 90 - I 270 ø -1

Wave. Train Zernike SRI 6

System-Level Parametric Studies • Types of Aberrations – Single Phase Screen Zernike Polynomials – Multi-Screen Distributed Atmosphere • Types of Tests – – Intensity Debalancing Image Misregistration Tilt Rejection Camera Signal to Noise Ratio (SNR) • Metric – Used measured wrapped wavefront to compensate the beam. – Measured Peak Strehl Ratio (PSR) • Ratio of peak intensity in the far-field for aberrated to that for a perfect beam 7
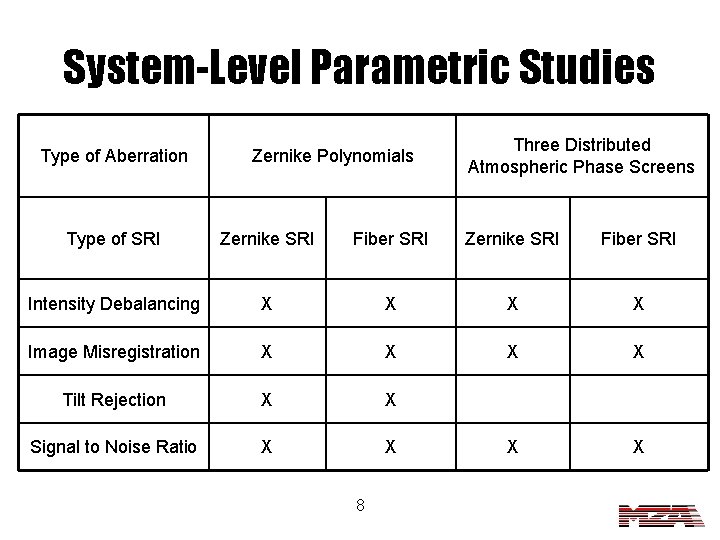
System-Level Parametric Studies Type of Aberration Zernike Polynomials Three Distributed Atmospheric Phase Screens Type of SRI Zernike SRI Fiber SRI Intensity Debalancing X X Image Misregistration X X Tilt Rejection X X Signal to Noise Ratio X X 8

System-Level Parametric Studies Type of Aberration Zernike Polynomials Three Distributed Atmospheric Phase Screens Type of SRI Zernike SRI Fiber SRI Intensity Debalancing X X Image Misregistration X X Tilt Rejection X X Signal to Noise Ratio X X 9

System Studies with Zernike Polynomial Phase Aberration Input 10
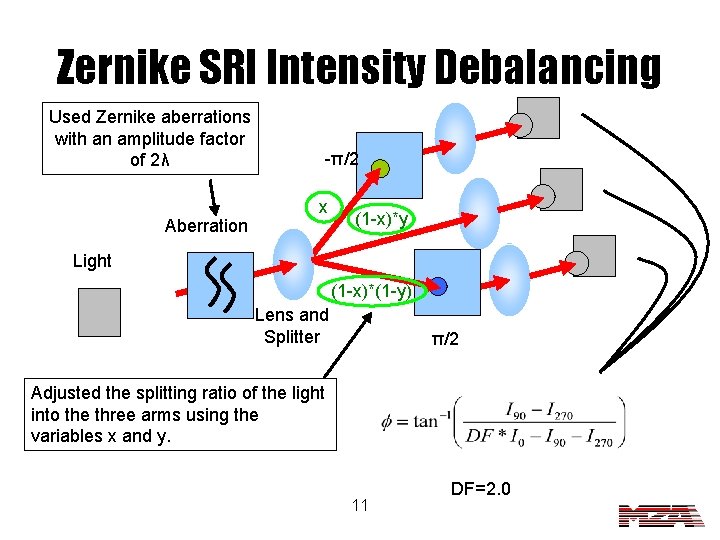
Zernike SRI Intensity Debalancing Used Zernike aberrations with an amplitude factor of 2λ Aberration -π/2 x (1 -x)*y Light (1 -x)*(1 -y) Lens and Splitter π/2 Adjusted the splitting ratio of the light into the three arms using the variables x and y. 11 DF=2. 0

Fiber SRI Intensity Debalancing 0 Lens π/2 Light π Aberration Splitter 3: 1 splitting ratio 3π/2 x Used Zernike aberrations with an amplitude factor of 0. 7λ (1 -x)*y (1 -x)*(1 -y)(1 -z) (1 -x)*(1 -y)*z Adjusted the splitting ratio of the input light into the four arms using the variables x, y, and z. 12
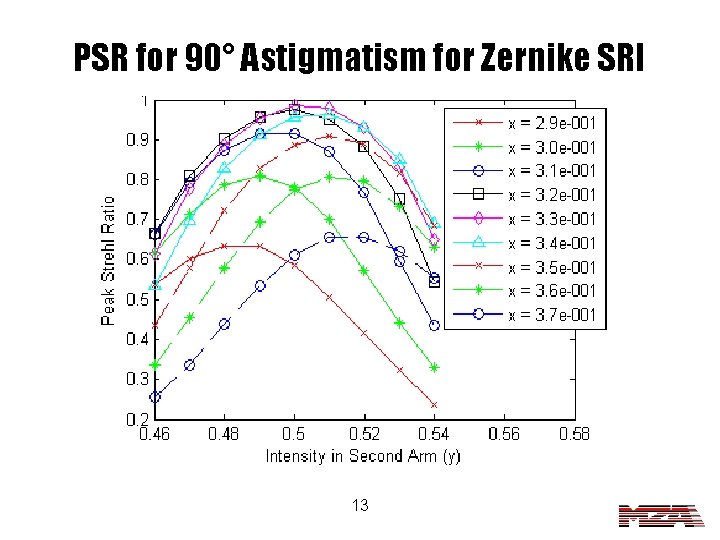
PSR for 90° Astigmatism for Zernike SRI 13
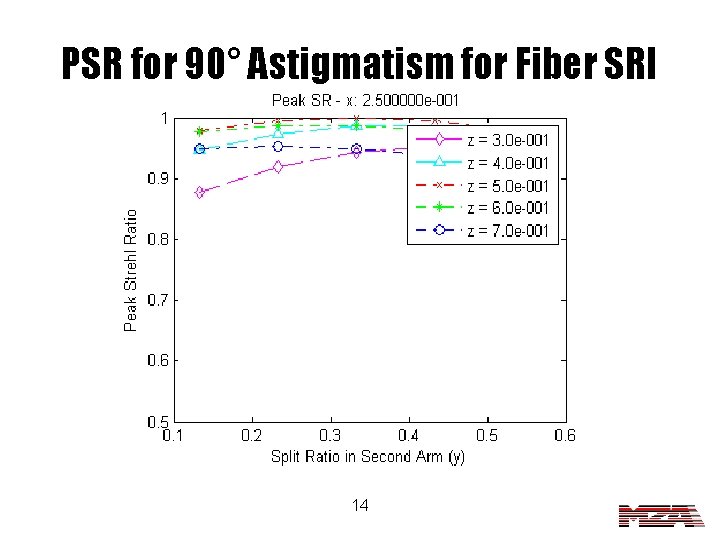
PSR for 90° Astigmatism for Fiber SRI 14
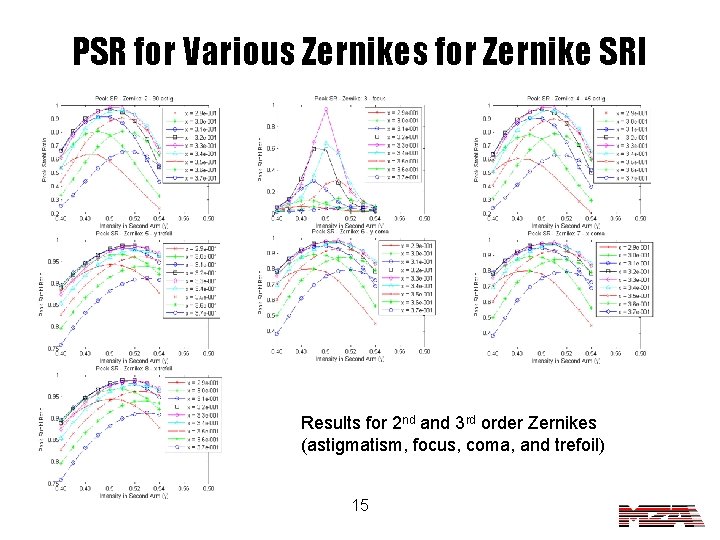
PSR for Various Zernikes for Zernike SRI Results for 2 nd and 3 rd order Zernikes (astigmatism, focus, coma, and trefoil) 15
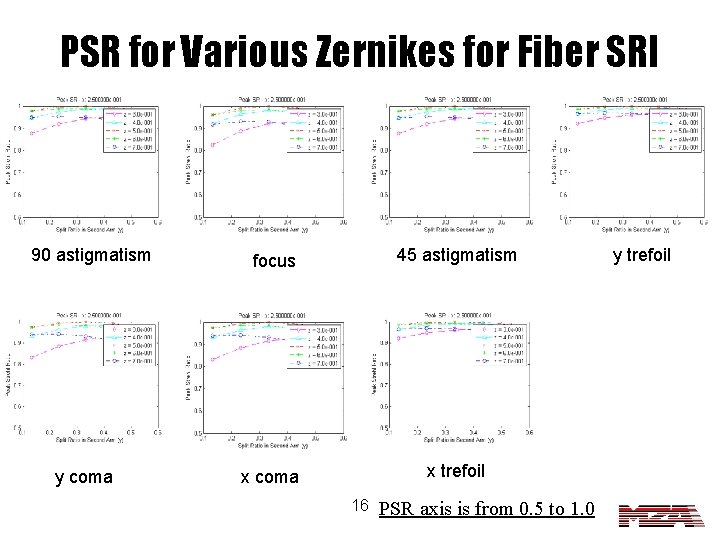
PSR for Various Zernikes for Fiber SRI 90 astigmatism y coma focus 45 astigmatism x coma x trefoil 16 PSR axis is from 0. 5 to 1. 0 y trefoil

Intensity Debalancing Conclusions • Zernike SRI is very sensitive to intensity debalancing – PSR varied by about 40% for a 4% change in the balancing of the 50/50 beam splitter. • Fiber SRI is fairly insensitive to intensity debalancing – PSR varied by about 1% for a 10% change in the balancing of the 50/50 beam splitter. 17
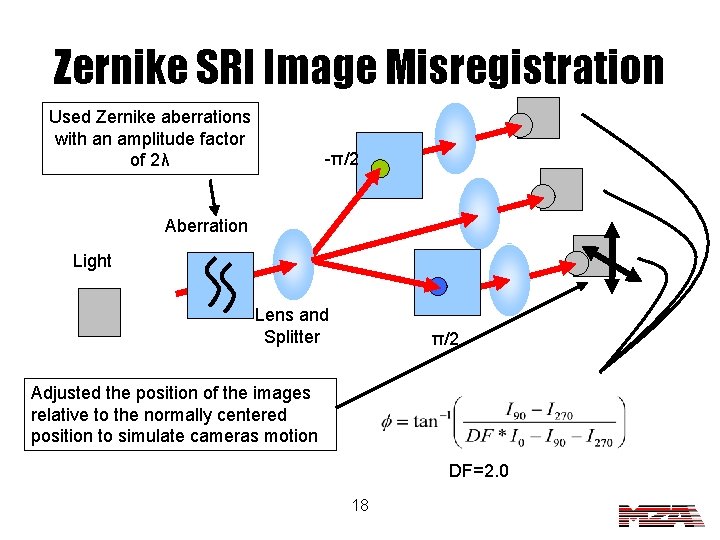
Zernike SRI Image Misregistration Used Zernike aberrations with an amplitude factor of 2λ -π/2 Aberration Light Lens and Splitter π/2 Adjusted the position of the images relative to the normally centered position to simulate cameras motion DF=2. 0 18
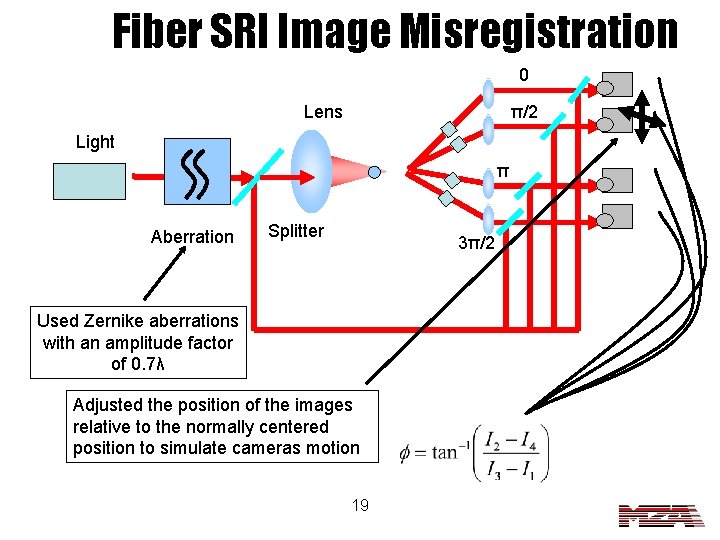
Fiber SRI Image Misregistration 0 Lens π/2 Light π Aberration Splitter 3π/2 Used Zernike aberrations with an amplitude factor of 0. 7λ Adjusted the position of the images relative to the normally centered position to simulate cameras motion 19
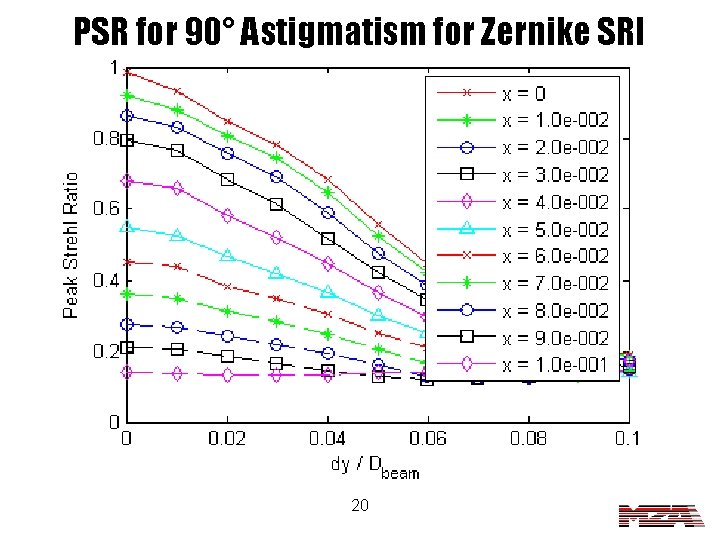
PSR for 90° Astigmatism for Zernike SRI 20
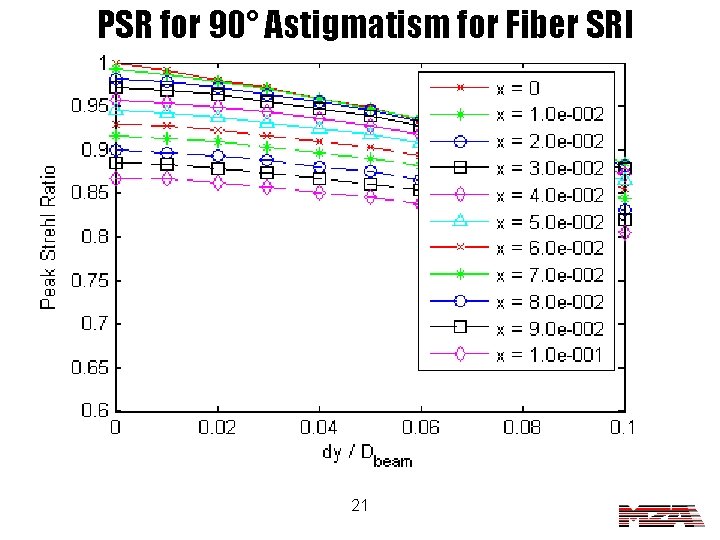
PSR for 90° Astigmatism for Fiber SRI 21
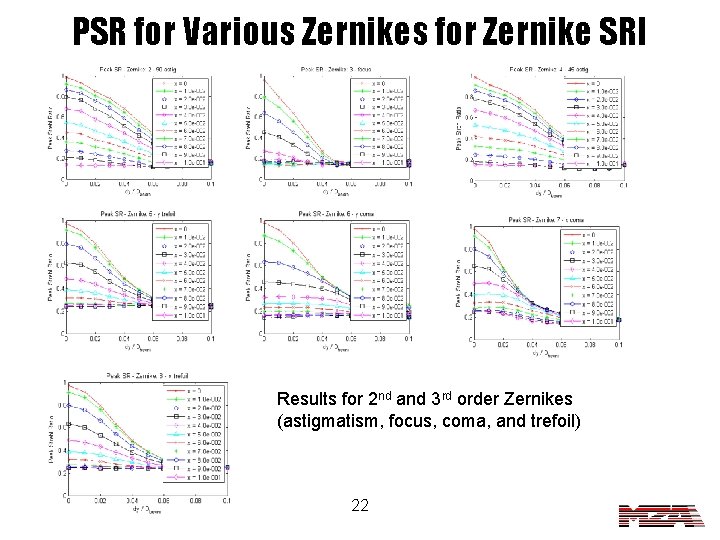
PSR for Various Zernikes for Zernike SRI Results for 2 nd and 3 rd order Zernikes (astigmatism, focus, coma, and trefoil) 22
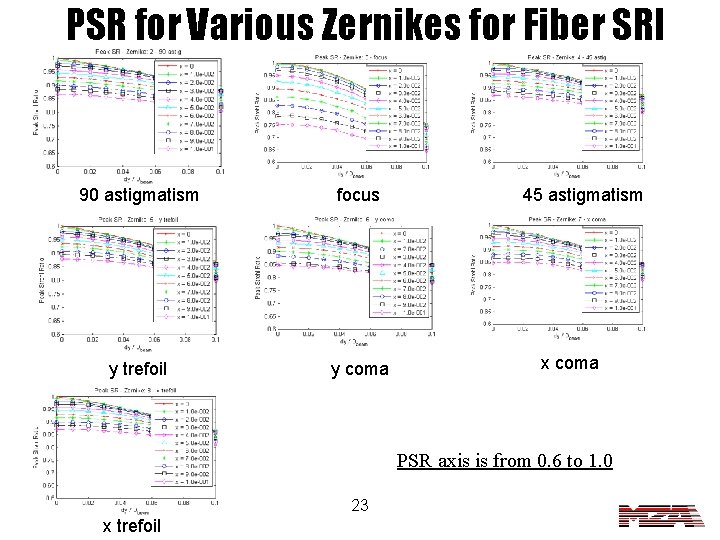
PSR for Various Zernikes for Fiber SRI 90 astigmatism focus y trefoil y coma 45 astigmatism x coma PSR axis is from 0. 6 to 1. 0 23 x trefoil

Image Misregistration Conclusions • Zernike SRI is sensitive to image misregistration of a single image. – Although some Zernike aberrations seemed to be more robust, most of the Zernikes saw a 20% reduction in Strehl ratio for a motion of 2% of the beam diameter • The Fiber SRI is fairly insensitive to image misregistration of a single image for all the Zernikes. – Most of the Zernikes saw a 2% reduction in Strehl ratio for a motion of 2% of the beam diameter. – 2% of the beam diameter corresponds to 160 μm on an 8 -mm diameter beam 24

Setup with Camera Noise • Number of Realizations = 30 • Input Aberration is 90 degree astigmatism • Maximum Count Value = 10 e 9 – Eliminates effect of discretization 25
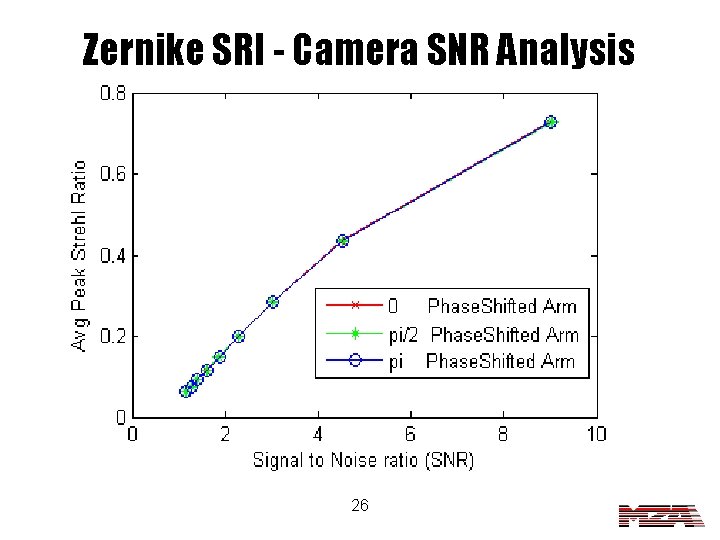
Zernike SRI - Camera SNR Analysis 26
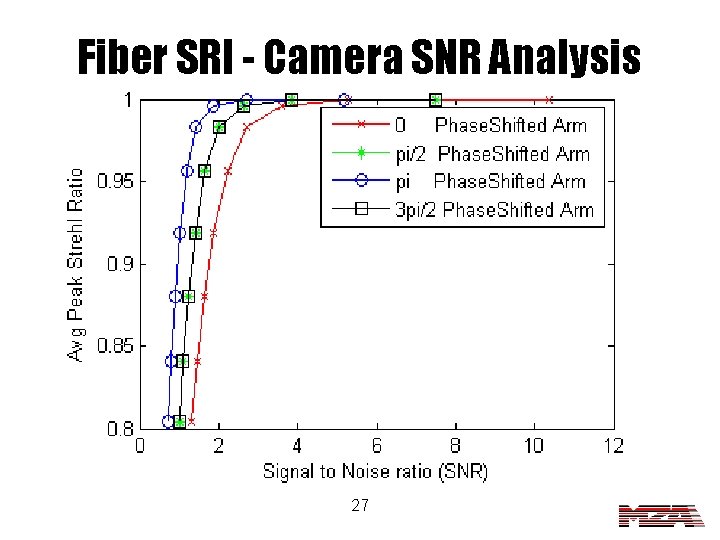
Fiber SRI - Camera SNR Analysis 27

SNR Conclusions • Zernike SRI seems to be very sensitive to camera noise. – The result might be due to the lack of frames over which to average – Maybe a 4 -bin Zernike SRI would have better noise performance • The fiber SRI seems to be very tolerant of noise. – The PSR dropped to 80% when the SNR was around 1. 0 28

System Studies with Distributed Atmosphere 29

Zernike SRI Image Misregistration for Atmospheric Aberrations Setup • We are using tilt-removed model of the atmosphere. • D / r 0 = {1, 2, 3, 4, 5} • Range = 2. 0 m • Fresnel Number = 5 • Denominator Factor – 6 for D / r 0 = 1, 2, and 3. – 2 for D / r 0 = 4, and 5. • Number of screens = 3 • Number of Realizations =9 30
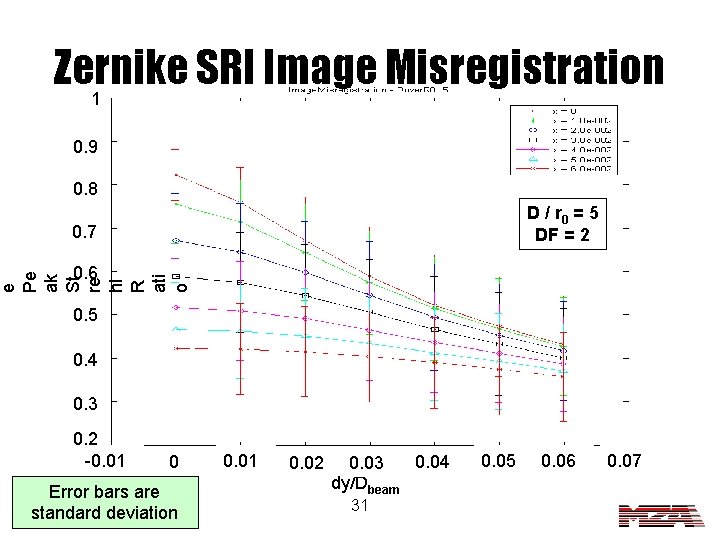
Zernike SRI Image Misregistration 1 0. 9 0. 8 D / r 0 = 5 DF = 2 0. 7 e Pe ak St re hl R ati o 0. 6 0. 5 0. 4 0. 3 0. 2 -0. 01 0 Error bars are standard deviation 0. 01 0. 02 0. 04 0. 03 dy/Dbeam 31 0. 05 0. 06 0. 07
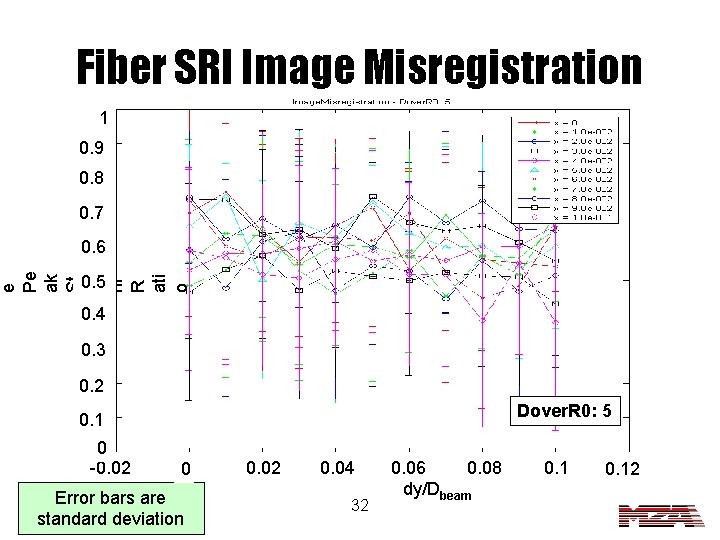
Fiber SRI Image Misregistration 1 0. 9 0. 8 0. 7 e Pe ak St re hl R ati o 0. 6 0. 5 0. 4 0. 3 0. 2 Dover. R 0: 5 0. 1 0 -0. 02 0 Error bars are standard deviation 0. 02 0. 04 32 0. 06 0. 08 dy/Dbeam 0. 12
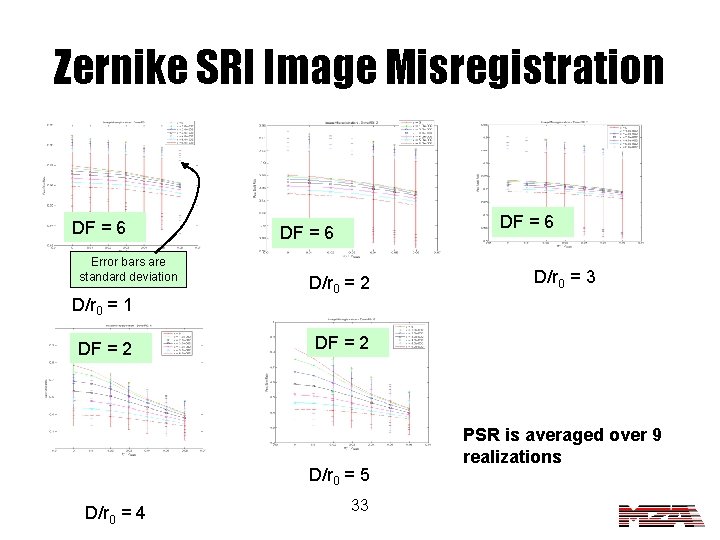
Zernike SRI Image Misregistration DF = 6 Error bars are standard deviation D/r 0 = 1 DF = 2 DF = 6 D/r 0 = 2 DF = 2 D/r 0 = 5 D/r 0 = 4 D/r 0 = 3 33 PSR is averaged over 9 realizations
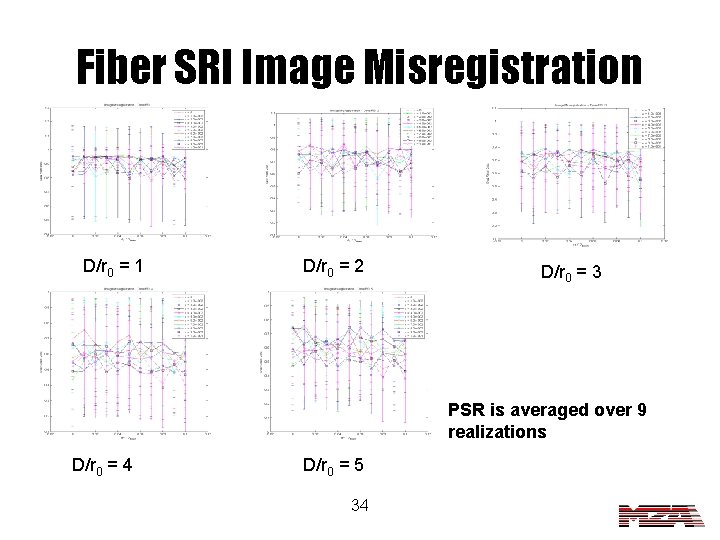
Fiber SRI Image Misregistration D/r 0 = 1 D/r 0 = 2 D/r 0 = 3 PSR is averaged over 9 realizations D/r 0 = 4 D/r 0 = 5 34

Image Misregistration Conclusions • For Zernike SRI, image misregistration effect increases with increasing turbulence. • Again, the fiber SRI seems to be very insensitive to the misalignment of a single detector. 35

Zernike SRI Setup with Camera Noise • • • Number of Realizations = 30 D/r 0 = 5 Range = 2 m Fresnel number = 5 Maximum Count Value = 10 e 9 – Eliminates the effect of discretization 36
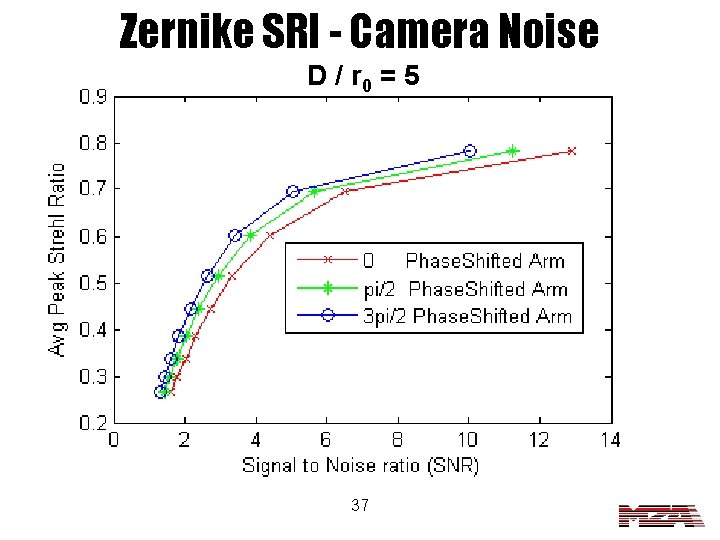
Zernike SRI - Camera Noise D / r 0 = 5 37
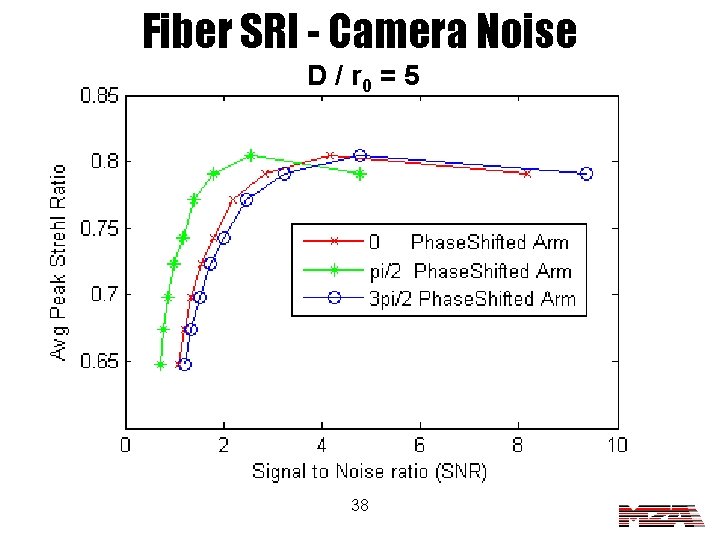
Fiber SRI - Camera Noise D / r 0 = 5 38

Atm. Camera Noise Conclusions • The Zernike SRI is sensitive to noise, but not as bad as with the astigmatism term tested earlier. • Again the noise performance seems to be better for the fiber SRI than for the Zernike SRI. 39
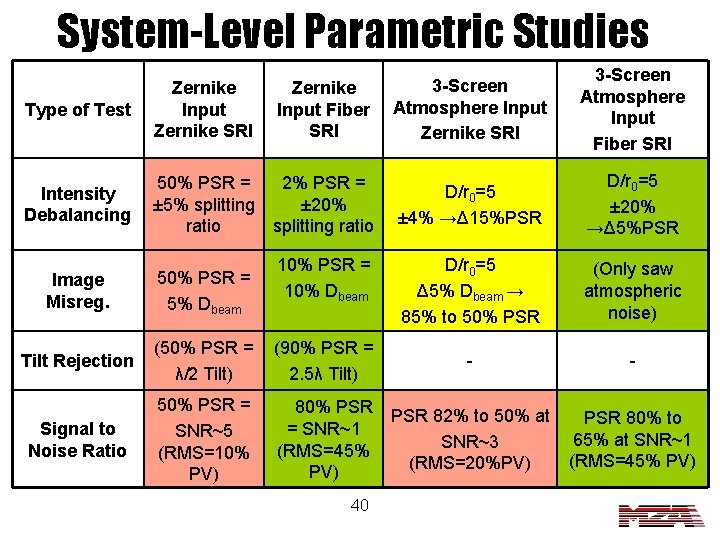
System-Level Parametric Studies Type of Test Zernike Input Zernike SRI Zernike Input Fiber SRI 3 -Screen Atmosphere Input Zernike SRI 3 -Screen Atmosphere Input Fiber SRI Intensity Debalancing 50% PSR = ± 5% splitting ratio 2% PSR = ± 20% splitting ratio D/r 0=5 ± 4% →Δ 15%PSR D/r 0=5 ± 20% →Δ 5%PSR Image Misreg. 50% PSR = 5% Dbeam 10% PSR = 10% Dbeam D/r 0=5 Δ 5% Dbeam → 85% to 50% PSR (Only saw atmospheric noise) Tilt Rejection (50% PSR = λ/2 Tilt) (90% PSR = 2. 5λ Tilt) - - Signal to Noise Ratio 50% PSR = SNR~5 (RMS=10% PV) 80% PSR = SNR~1 (RMS=45% PV) PSR 82% to 50% at SNR~3 (RMS=20%PV) PSR 80% to 65% at SNR~1 (RMS=45% PV) 40

SRI Comparison Overview • In almost every comparison between the 3 -bin Zernike SRI and the 4 -bin fiber SRI, the fiber SRI had better performance. • Future Work: – Compare a 4 -bin fiber SRI to a 4 -bin Zernike SRI. – Complete rigorous AO study with both devices. 41

Questions? (505) 245 -9970 x 137 42

Backup Slides 43
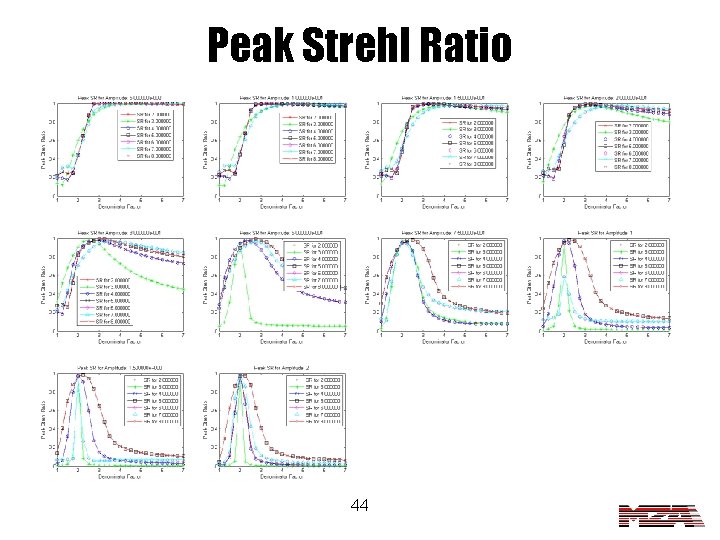
Peak Strehl Ratio 44
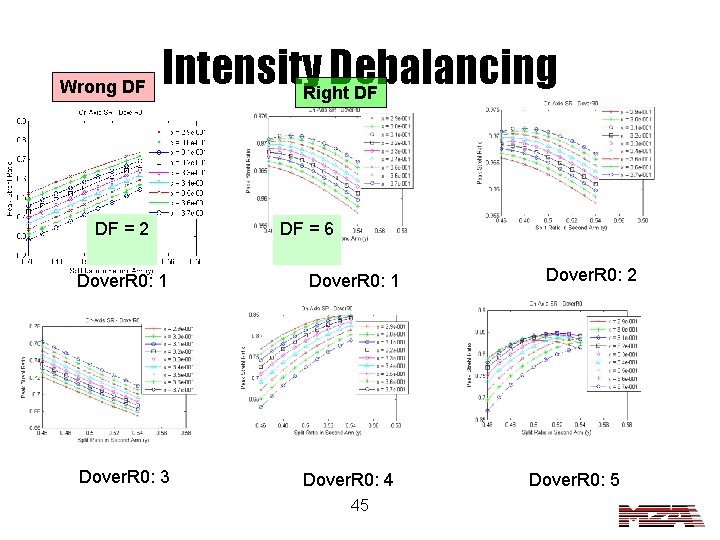
Wrong DF Intensity. Right. Debalancing DF DF = 2 Dover. R 0: 1 Dover. R 0: 3 DF = 6 Dover. R 0: 1 Dover. R 0: 4 45 Dover. R 0: 2 Dover. R 0: 5
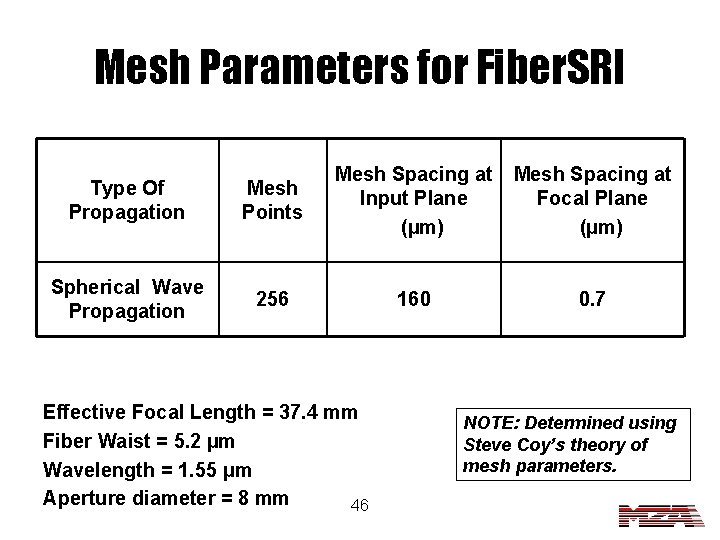
Mesh Parameters for Fiber. SRI Type Of Propagation Mesh Points Mesh Spacing at Input Plane (µm) Mesh Spacing at Focal Plane (µm) Spherical Wave Propagation 256 160 0. 7 Effective Focal Length = 37. 4 mm Fiber Waist = 5. 2 µm Wavelength = 1. 55 μm Aperture diameter = 8 mm 46 NOTE: Determined using Steve Coy’s theory of mesh parameters.
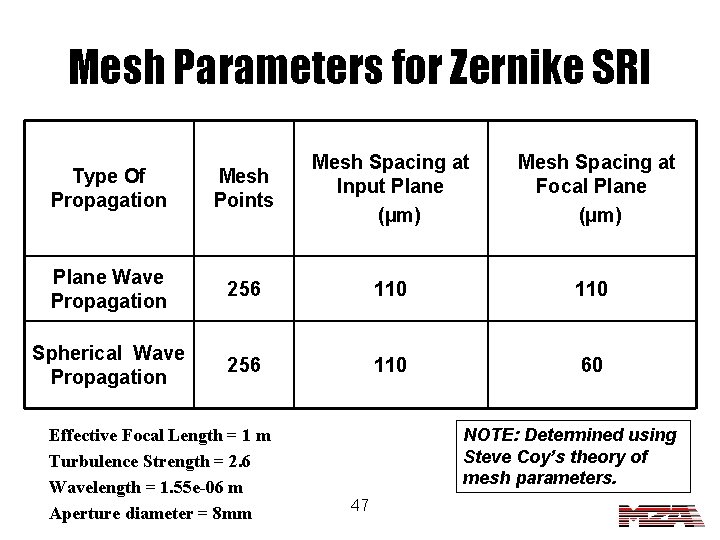
Mesh Parameters for Zernike SRI Type Of Propagation Mesh Points Mesh Spacing at Input Plane (µm) Mesh Spacing at Focal Plane (µm) Plane Wave Propagation 256 110 Spherical Wave Propagation 256 110 60 Effective Focal Length = 1 m Turbulence Strength = 2. 6 Wavelength = 1. 55 e-06 m Aperture diameter = 8 mm NOTE: Determined using Steve Coy’s theory of mesh parameters. 47

New Test System Components • Ideal Compensator – Used to apply the conjugate of the measured phase to the beam. – Operates like an ideal deformable mirror. • Peak Strehl Ratio Meter – Used to calculate the ratio of the peak intensity of the far-field spot with the residual aberration remaining after ideal compensation to that without any aberration. – We also used on-axis Strehl ratio which was calculated using the discrete version of the integral form. 48

Fiber SRI Intensity Debalancing for Atmospheric Aberrations Setup • We are using tilt-removed model of atmosphere • Range = 3. 45 m • Frenel number = 3 • Number of Screens = 3 • Number of Realizations = 8 • Data is recorded for low , medium and high turbulence. - D/r 0 = {1, 2, 3, 4, 5} 49

Fiber SRI Intensity Debalancing Conclusions • Often saw increase in performance by adjusting splitting ratios. – Saw a similar result with Zernike SRI • More investigation needs to be done here to determine the reason for this effect. 50

Image Misregistration Setup • We are using tilt-removed model of the atmosphere. • D / r 0 = {1, 2, 3, 4, 5} • Denominator Factor – 6 for D / r 0 = 1, 2, and 3. – 2 for D / r 0 = 4, and 5. • Moving Image at 4 bin processing from 0 to 0. 6 times input beam diameter. • Number of Screens = 3 51
- Slides: 51