Comparison Networks Sorting Sorting binary values Sorting arbitrary

Comparison Networks Sorting • Sorting binary values • Sorting arbitrary numbers • Implementing symmetric functions
![Sorting Algorithms Example Mergesort(array[1, …, n] of Integers): begin Mergesort(array[1, …, n/2]); Mergesort(array[n/2+1, …, Sorting Algorithms Example Mergesort(array[1, …, n] of Integers): begin Mergesort(array[1, …, n/2]); Mergesort(array[n/2+1, …,](http://slidetodoc.com/presentation_image_h2/75af33da1caa26212336f6330f4af402/image-2.jpg)
Sorting Algorithms Example Mergesort(array[1, …, n] of Integers): begin Mergesort(array[1, …, n/2]); Mergesort(array[n/2+1, …, n]); Merge(array[1, …, n/2], array[n/2+1, …, n]); end comparisons required to merge two arrays of size m/2 comparisons to sort n elements Order of comparisons not fixed in advance. Not readily implementable in hardware.
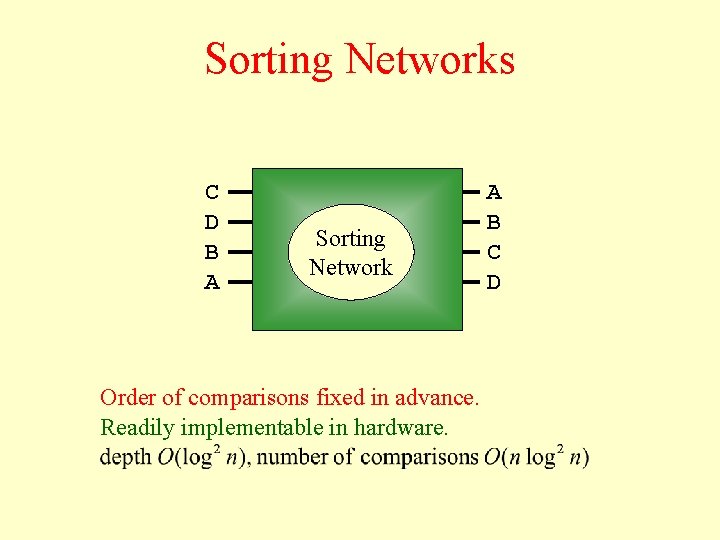
Sorting Networks C D B A Sorting Network Order of comparisons fixed in advance. Readily implementable in hardware. A B C D
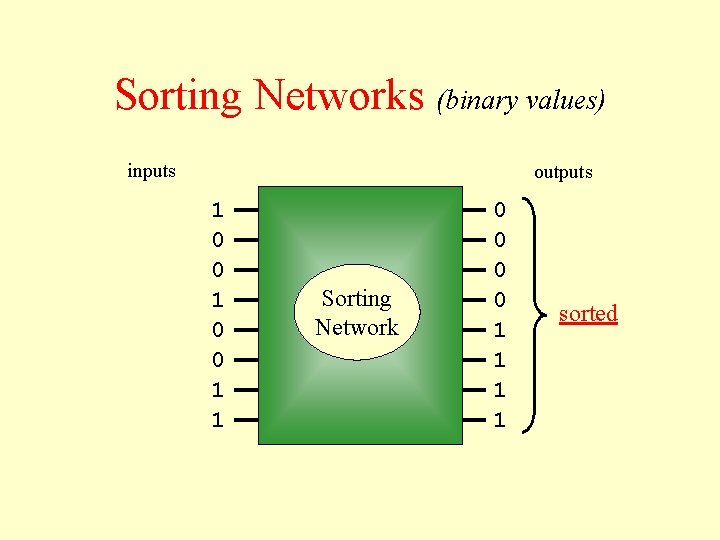
Sorting Networks (binary values) inputs outputs 1 0 0 1 1 Sorting Network 0 0 1 1 sorted
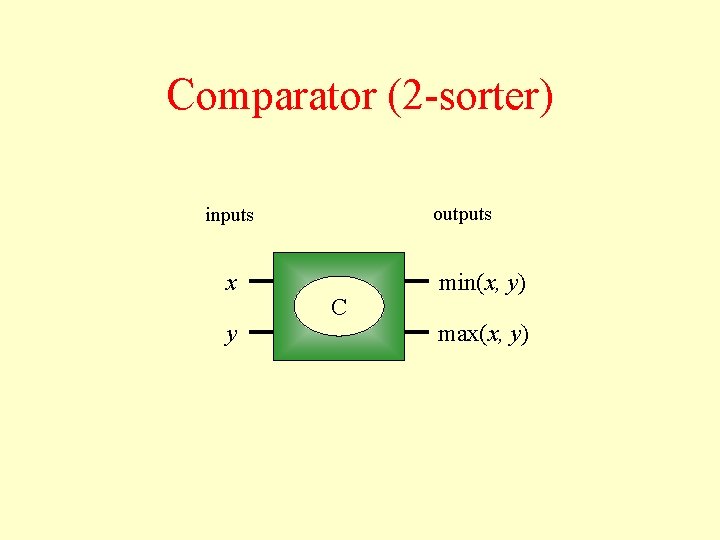
Comparator (2 -sorter) outputs inputs x y C min(x, y) max(x, y)
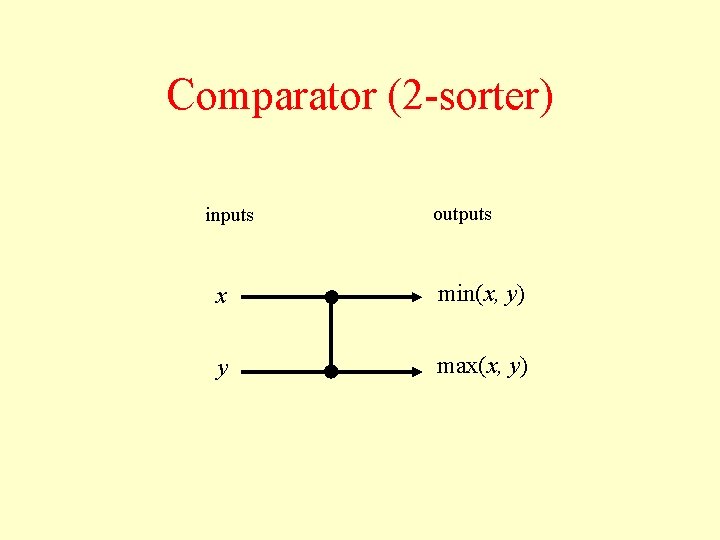
Comparator (2 -sorter) inputs outputs x min(x, y) y max(x, y)
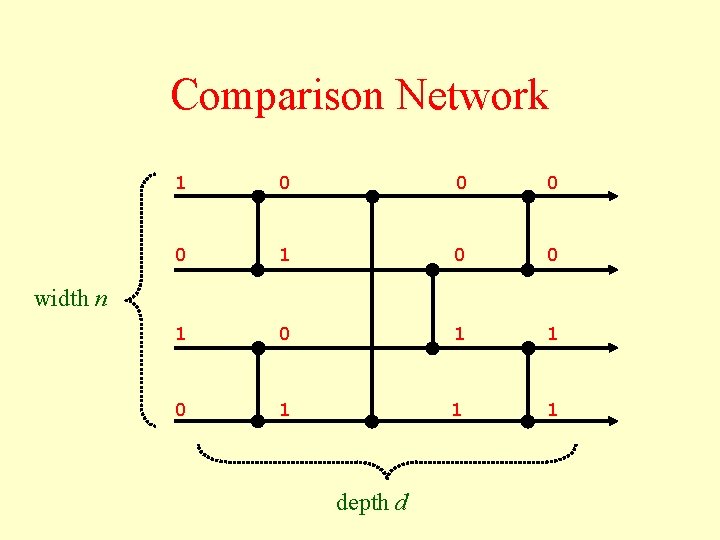
Comparison Network 1 0 0 1 1 0 1 1 1 width n depth d
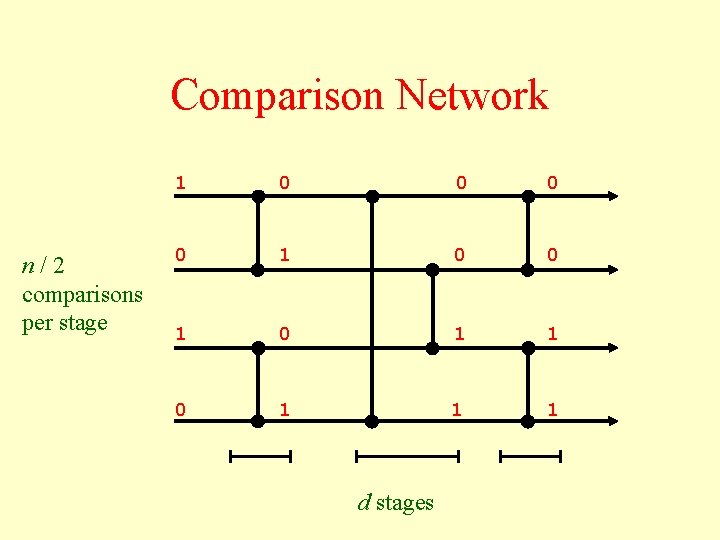
Comparison Network n/2 comparisons per stage 1 0 0 1 1 0 1 1 1 d stages

Sorting Network Any ideas?
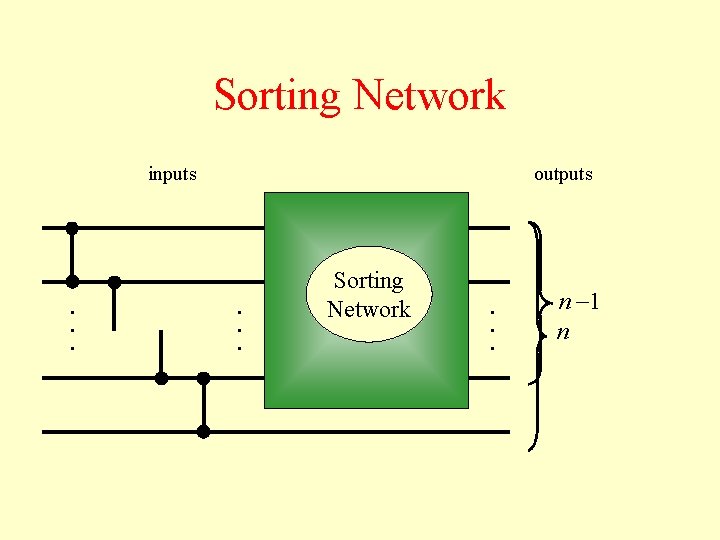
Sorting Network inputs . . . outputs . . . Sorting Network . . . n 1 n
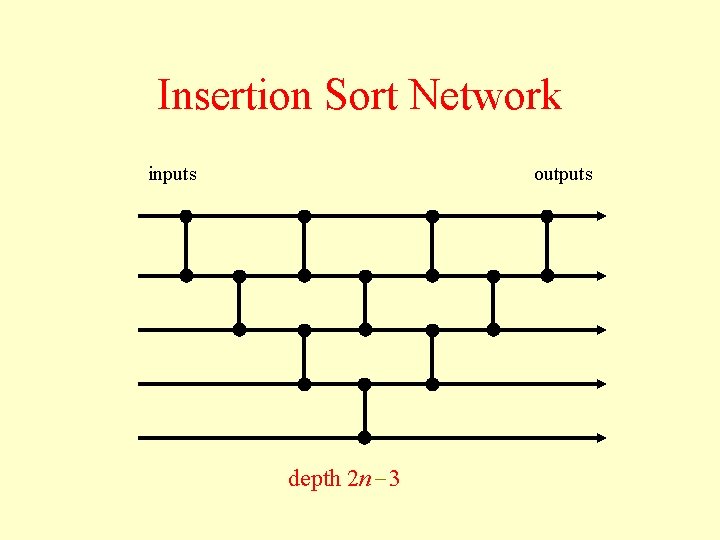
Insertion Sort Network inputs outputs depth 2 n 3
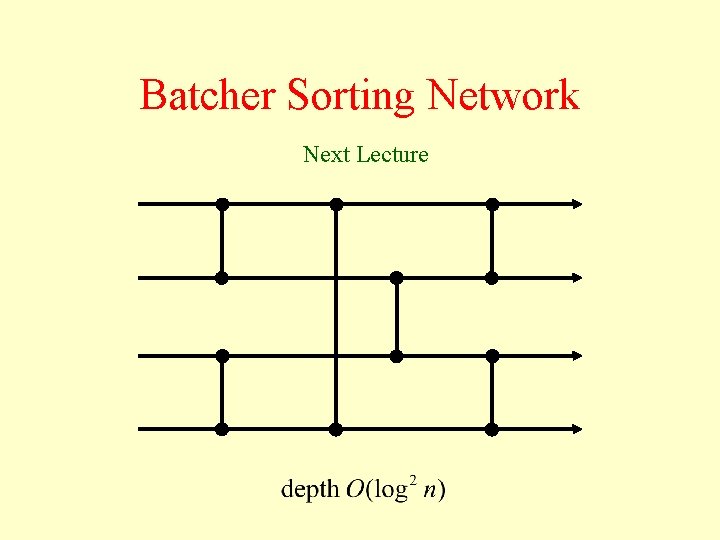
Batcher Sorting Network Next Lecture
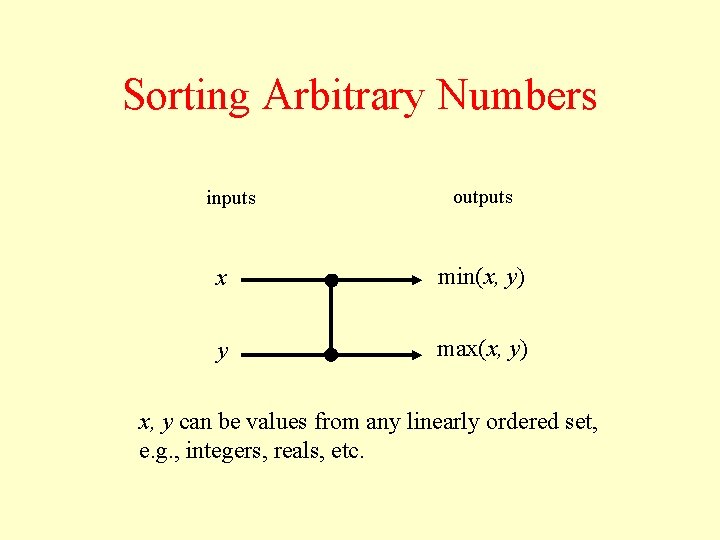
Sorting Arbitrary Numbers inputs outputs x min(x, y) y max(x, y) x, y can be values from any linearly ordered set, e. g. , integers, reals, etc.

Integer Comparator X, Y: integers represented as m-bit binary strings. Comparison function: C(X, Y) = 1 if X > Y, 0 otherwise. Idea: use C(X, Y) to select the min and the max of X and Y.
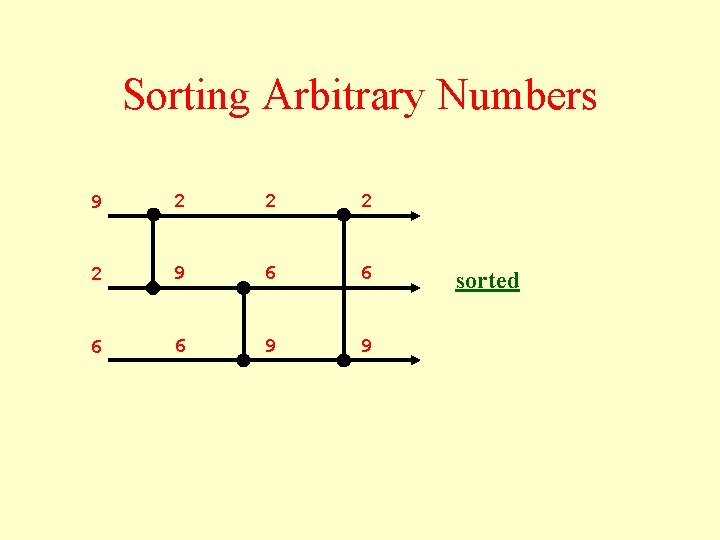
Sorting Arbitrary Numbers 9 2 2 9 6 6 9 9 sorted
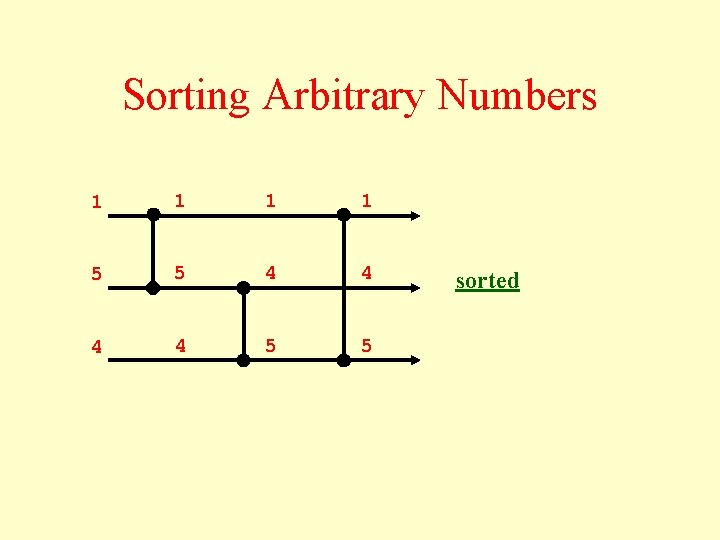
Sorting Arbitrary Numbers 1 1 5 5 4 4 5 5 sorted
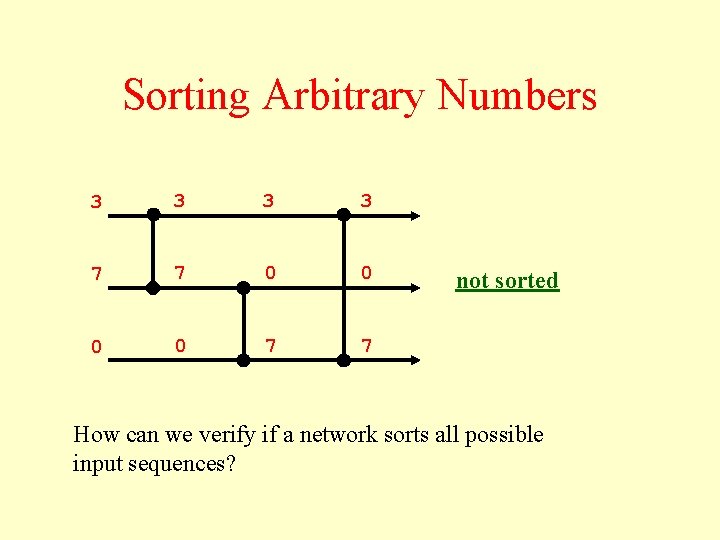
Sorting Arbitrary Numbers 3 3 7 7 0 0 7 7 not sorted How can we verify if a network sorts all possible input sequences?
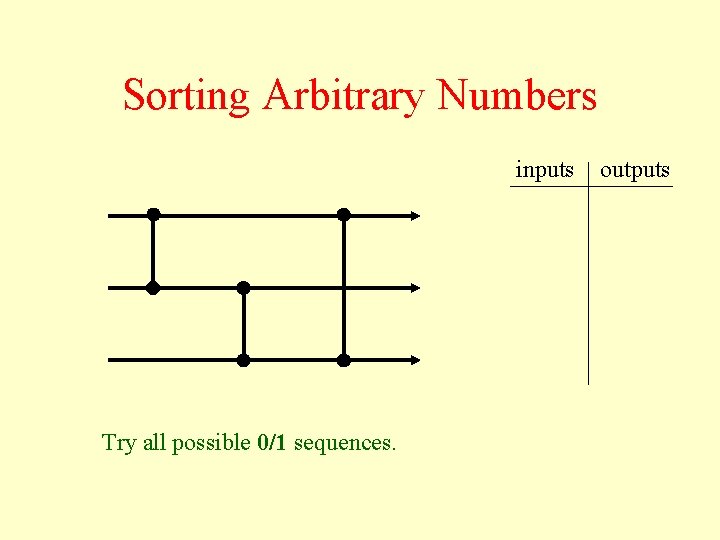
Sorting Arbitrary Numbers inputs Try all possible 0/1 sequences. outputs
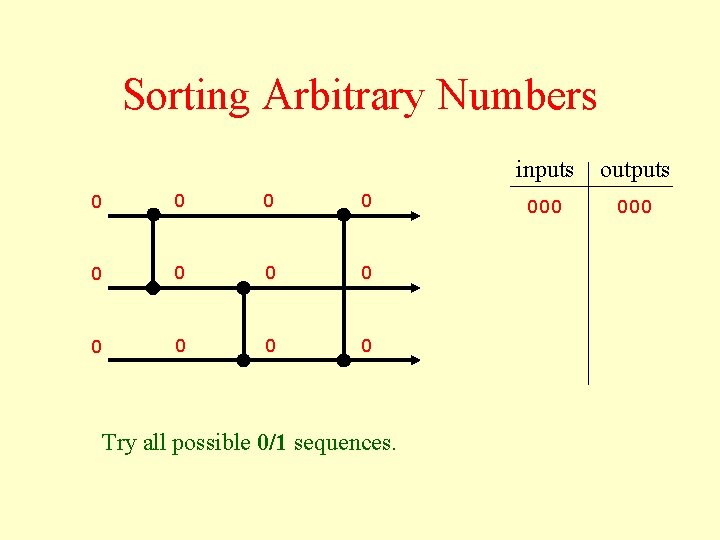
Sorting Arbitrary Numbers 0 0 0 Try all possible 0/1 sequences. inputs outputs 000
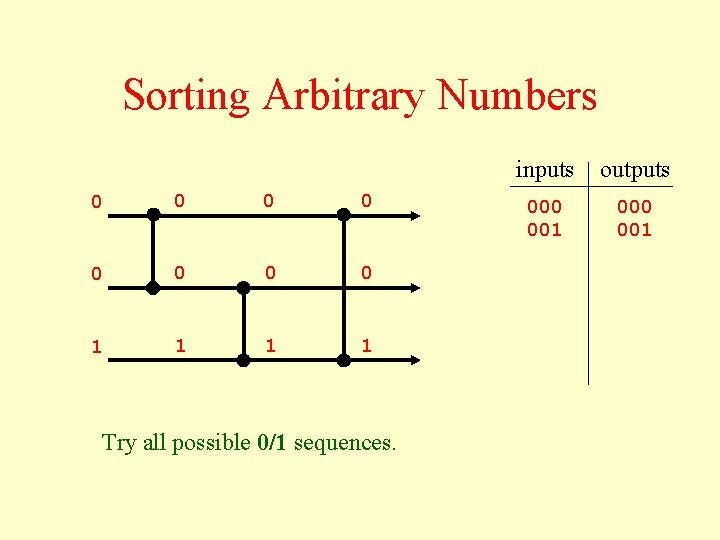
Sorting Arbitrary Numbers 0 0 0 0 1 1 Try all possible 0/1 sequences. inputs outputs 000 001
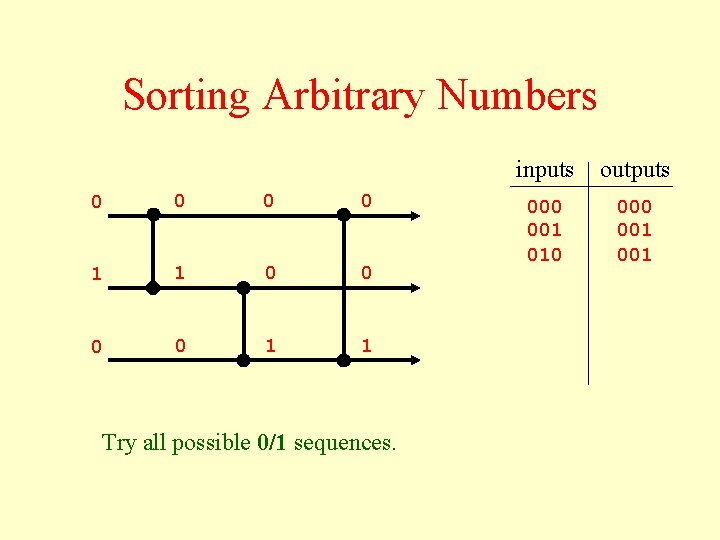
Sorting Arbitrary Numbers 0 0 0 0 1 1 Try all possible 0/1 sequences. inputs outputs 000 001 010 001 001
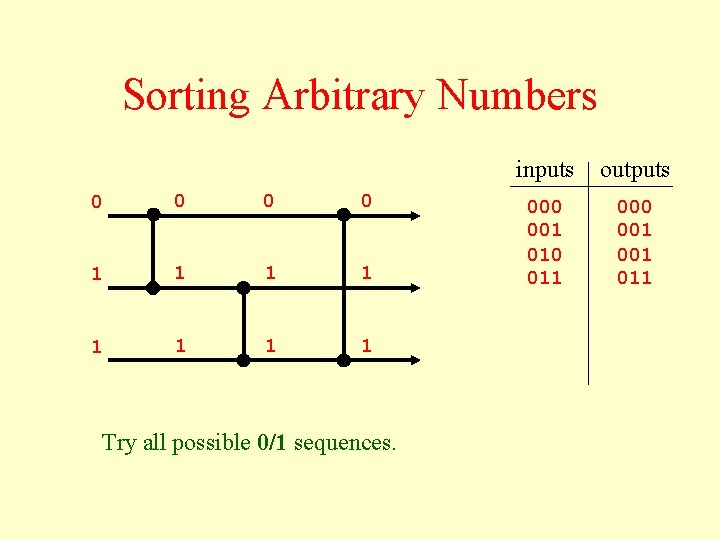
Sorting Arbitrary Numbers 0 0 1 1 1 1 Try all possible 0/1 sequences. inputs outputs 000 001 010 011 000 001 011
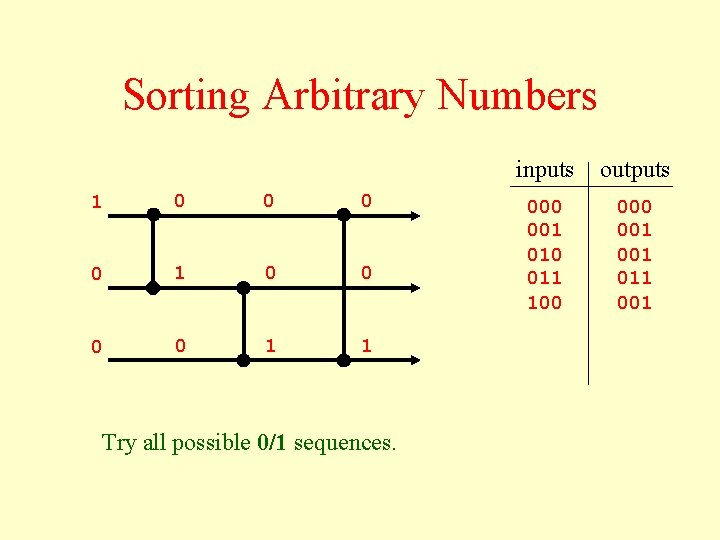
Sorting Arbitrary Numbers 1 0 0 0 0 1 1 Try all possible 0/1 sequences. inputs outputs 000 001 010 011 100 001 011 001
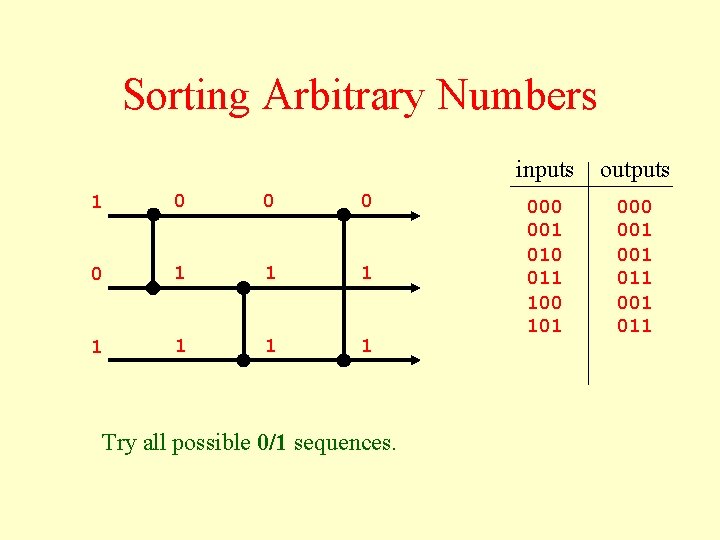
Sorting Arbitrary Numbers 1 0 0 1 1 1 1 Try all possible 0/1 sequences. inputs outputs 000 001 010 011 100 101 000 001 011
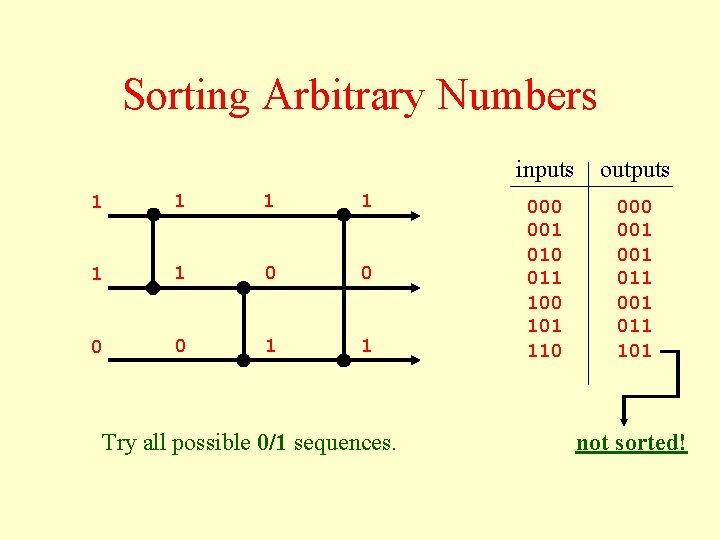
Sorting Arbitrary Numbers 1 1 1 0 0 1 1 Try all possible 0/1 sequences. inputs outputs 000 001 010 011 100 101 110 001 001 011 101 not sorted!
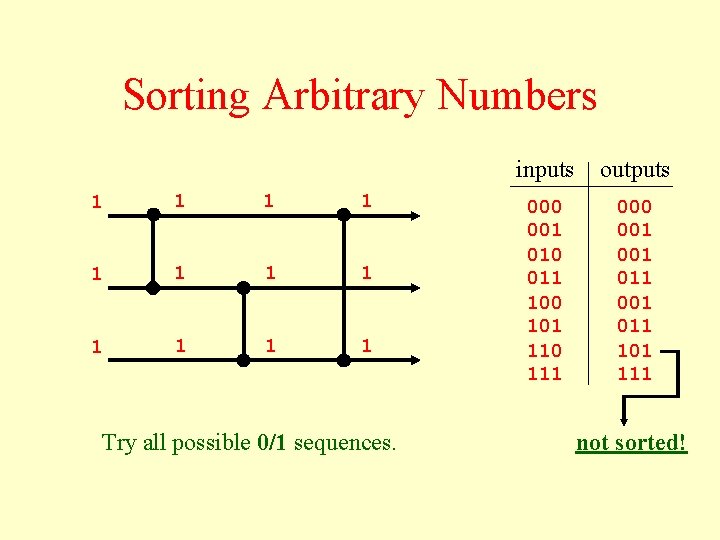
Sorting Arbitrary Numbers 1 1 1 Try all possible 0/1 sequences. inputs outputs 000 001 010 011 100 101 110 111 000 001 011 101 111 not sorted!
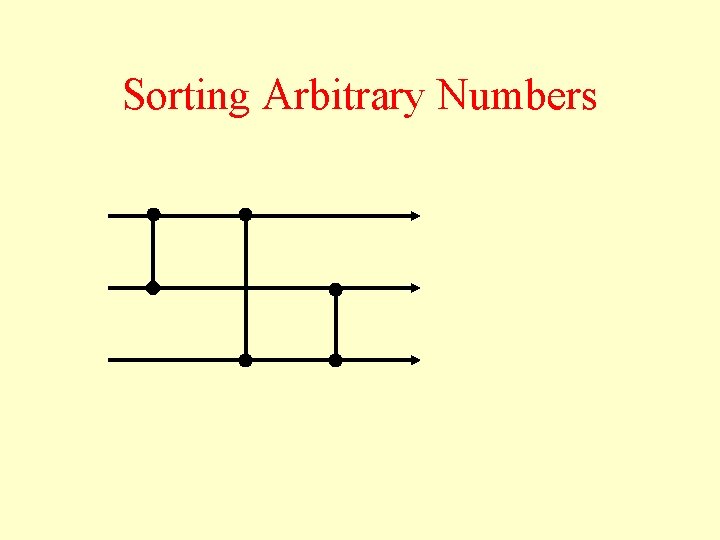
Sorting Arbitrary Numbers
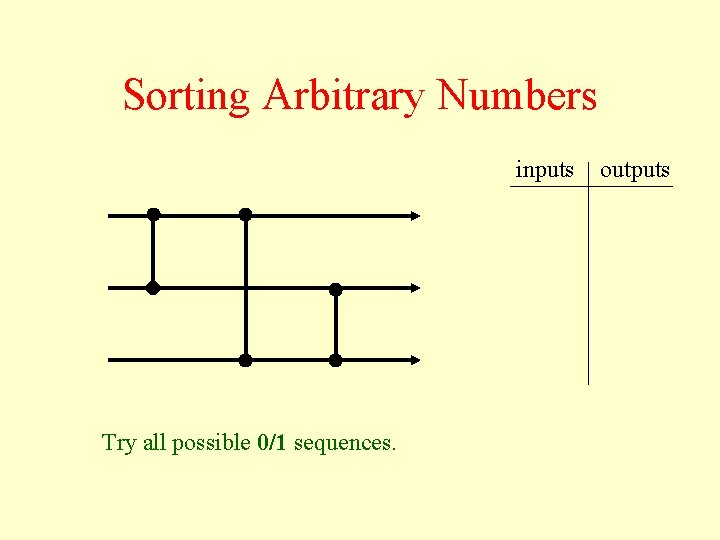
Sorting Arbitrary Numbers inputs Try all possible 0/1 sequences. outputs
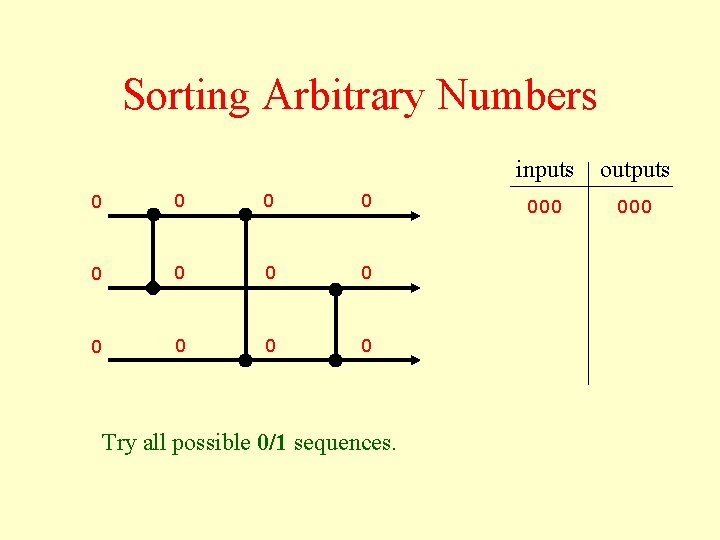
Sorting Arbitrary Numbers 0 0 0 Try all possible 0/1 sequences. inputs outputs 000
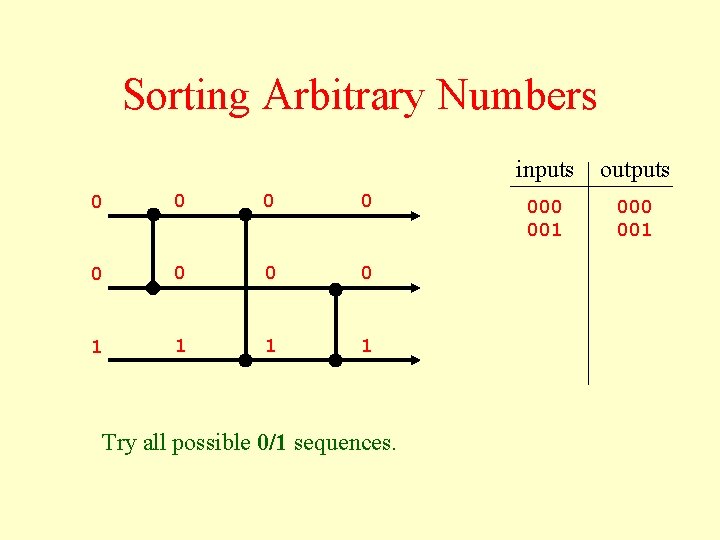
Sorting Arbitrary Numbers 0 0 0 0 1 1 Try all possible 0/1 sequences. inputs outputs 000 001
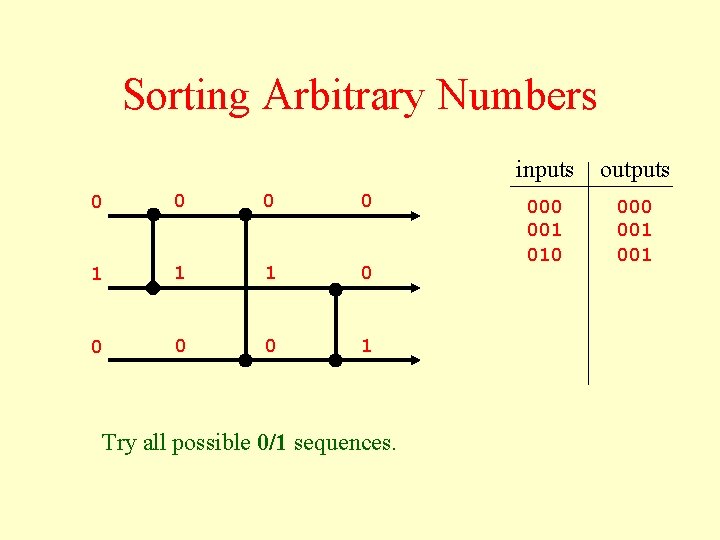
Sorting Arbitrary Numbers 0 0 1 1 1 0 0 1 Try all possible 0/1 sequences. inputs outputs 000 001 010 001 001
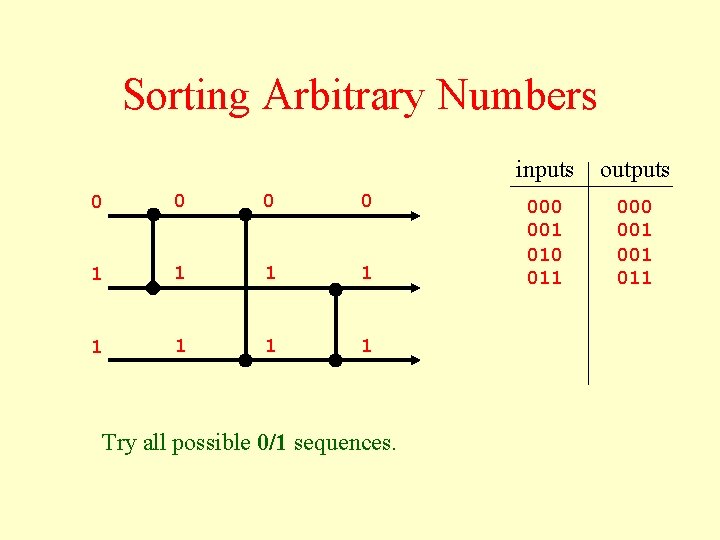
Sorting Arbitrary Numbers 0 0 1 1 1 1 Try all possible 0/1 sequences. inputs outputs 000 001 010 011 000 001 011
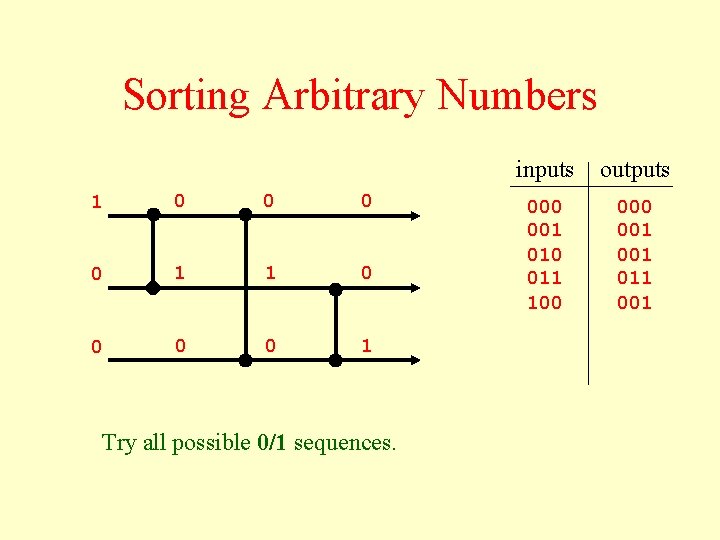
Sorting Arbitrary Numbers 1 0 0 0 0 1 Try all possible 0/1 sequences. inputs outputs 000 001 010 011 100 001 011 001
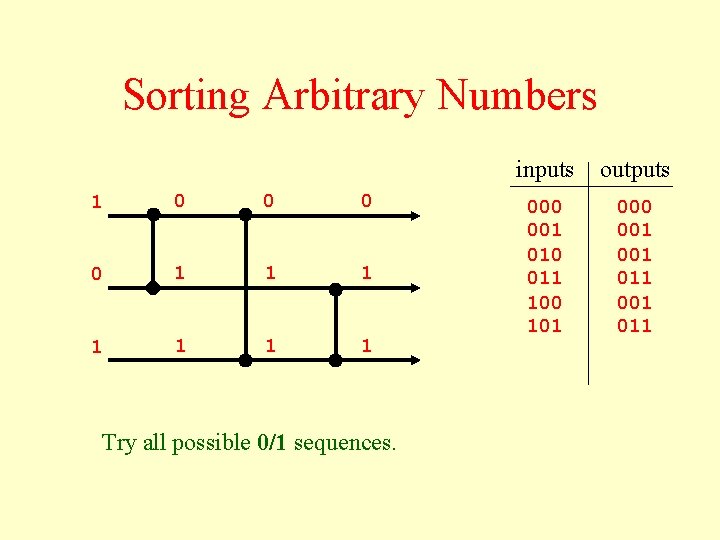
Sorting Arbitrary Numbers 1 0 0 1 1 1 1 Try all possible 0/1 sequences. inputs outputs 000 001 010 011 100 101 000 001 011
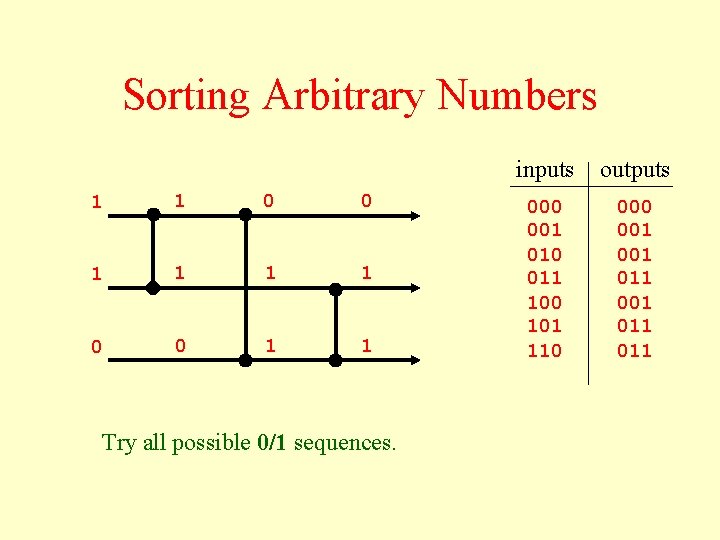
Sorting Arbitrary Numbers 1 1 0 0 1 1 Try all possible 0/1 sequences. inputs outputs 000 001 010 011 100 101 110 001 001 011 011
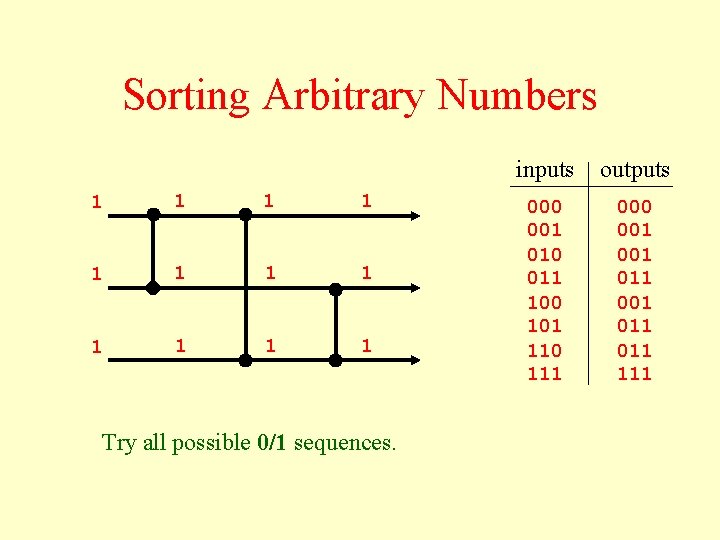
Sorting Arbitrary Numbers 1 1 1 Try all possible 0/1 sequences. inputs outputs 000 001 010 011 100 101 110 111 000 001 011 111

Sorting Arbitrary Numbers Try all possible 0/1 sequences. inputs outputs 000 001 010 011 100 101 110 111 000 001 011 111 all sorted!

Zero-One Principle If a comparison network sorts all possible sequences of 0’s and 1’s correctly, then it sorts all sequences of arbitrary numbers correctly.

Lemma Given For a monotonically increasing function f,

Lemma Given For a monotonically increasing function f,

Proof: Lemma

Proof: Lemma

Proof: Lemma f is monotonically increasing:

Proof: Lemma f is monotonically increasing:

Proof: Lemma f is monotonically increasing:
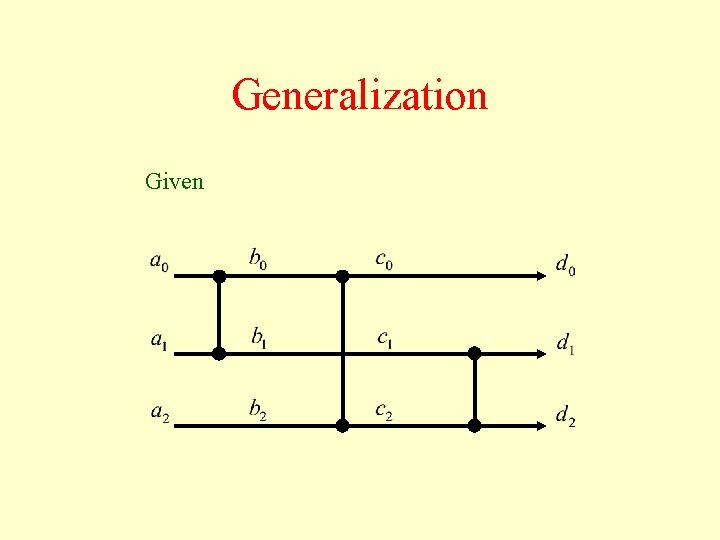
Generalization Given
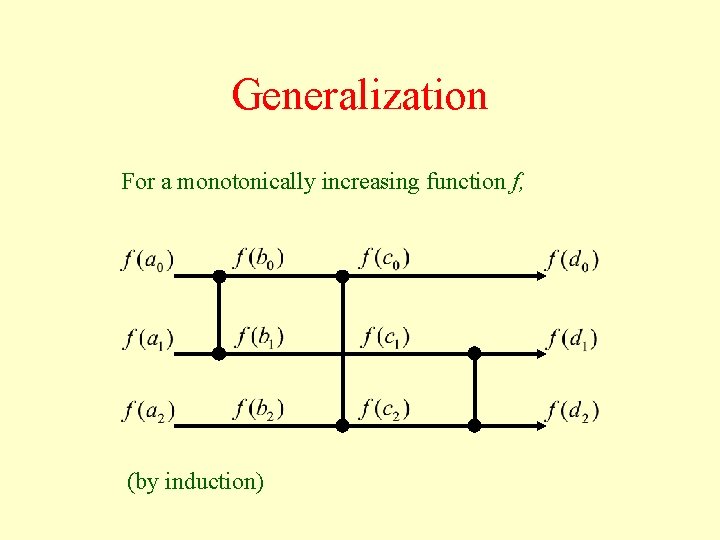
Generalization For a monotonically increasing function f, (by induction)

Proof: Zero-One Principle Suppose a) the network sorts all sequences of 0’s and 1’s, b) there exists a sequence that it doesn’t sort, i. e. , but such that is placed before Define f (x) = 0 if 1 otherwise in the output.

Proof: Zero-One Principle . . . Sorting Network . . .
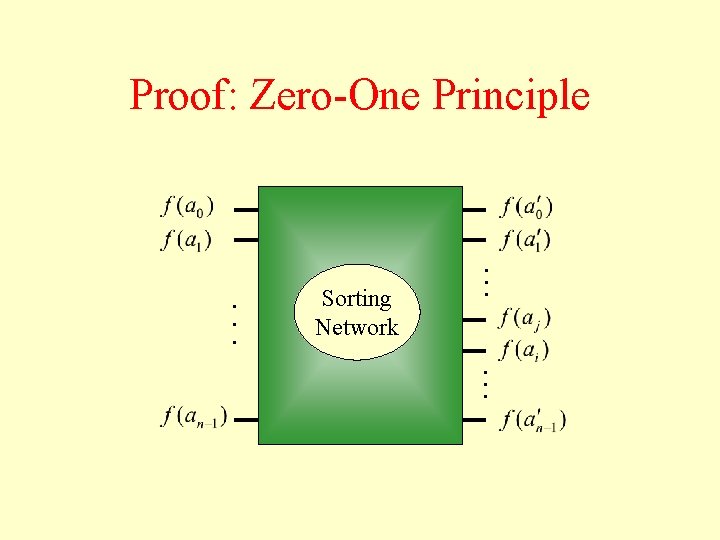
Proof: Zero-One Principle . . . Sorting Network . . .
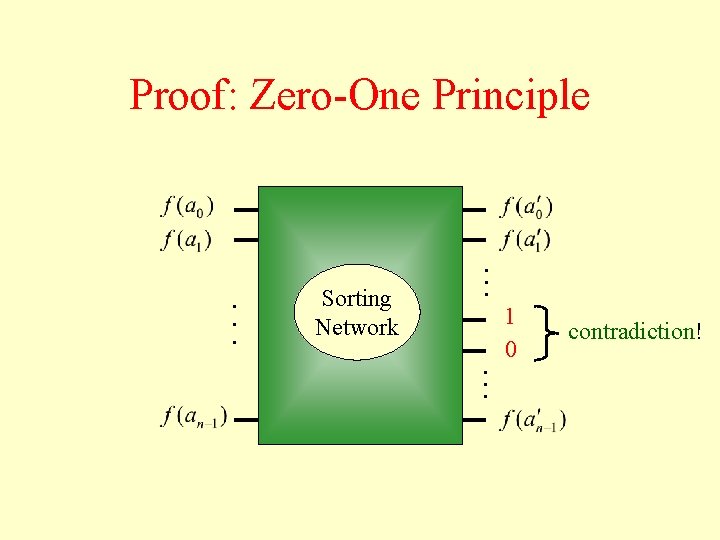
Proof: Zero-One Principle . . . Sorting Network . . . 1 0 contradiction!
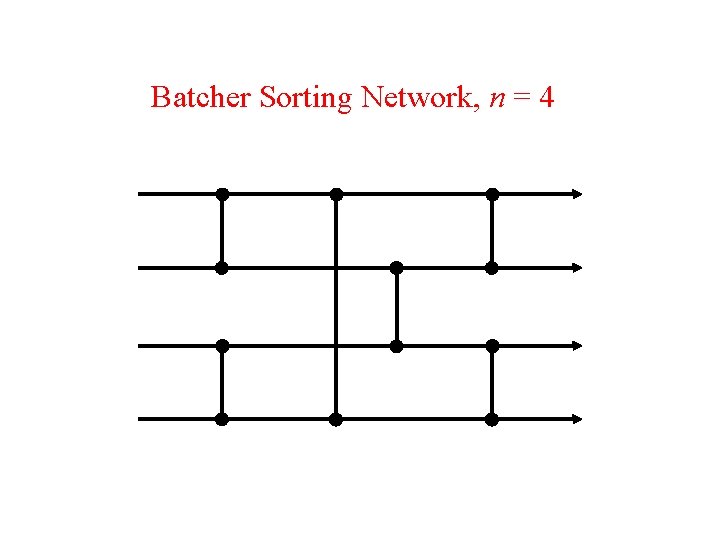
Batcher Sorting Network, n = 4
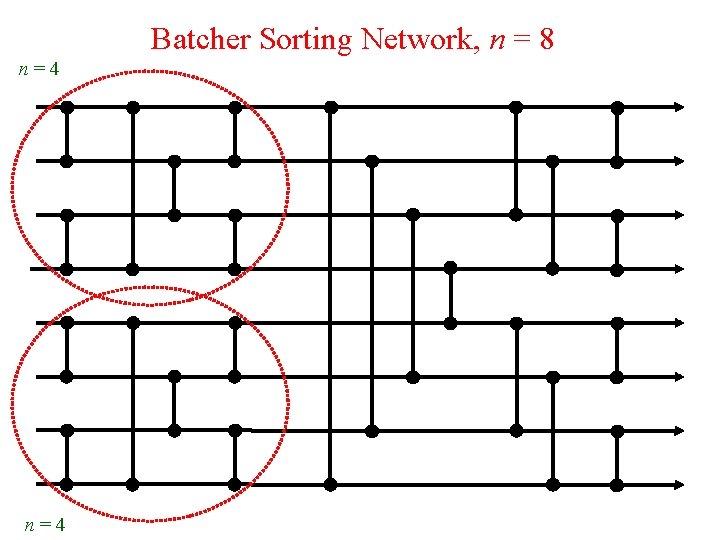
Batcher Sorting Network, n = 8 n=4
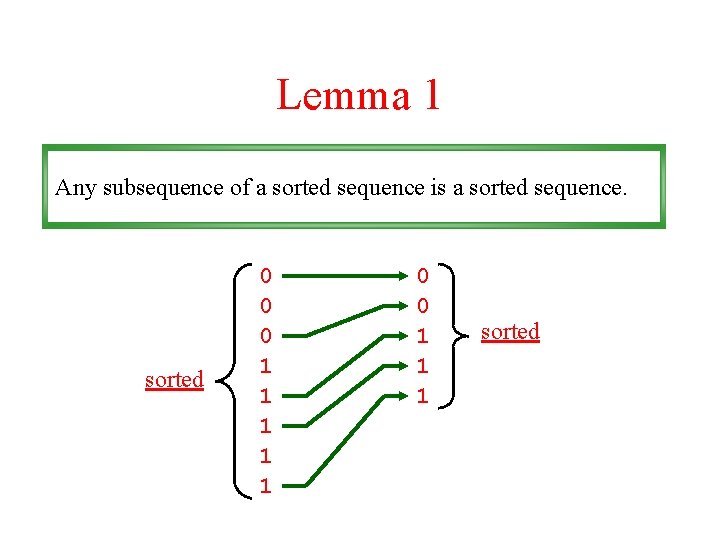
Lemma 1 Any subsequence of a sorted sequence is a sorted sequence. sorted 0 0 0 1 1 1 sorted

Lemma 2 For a sorted sequence, the number of 0’s in the even subsequence is either equal to, or one greater than, the number of 0’s in the odd subsequence. sorted 0 0 0 0 0 1 1 1 even odd

Lemma 3 For two sorted sequences and : denotes the number of 0’s in denotes the even subsequence of denotes the odd subsequence of
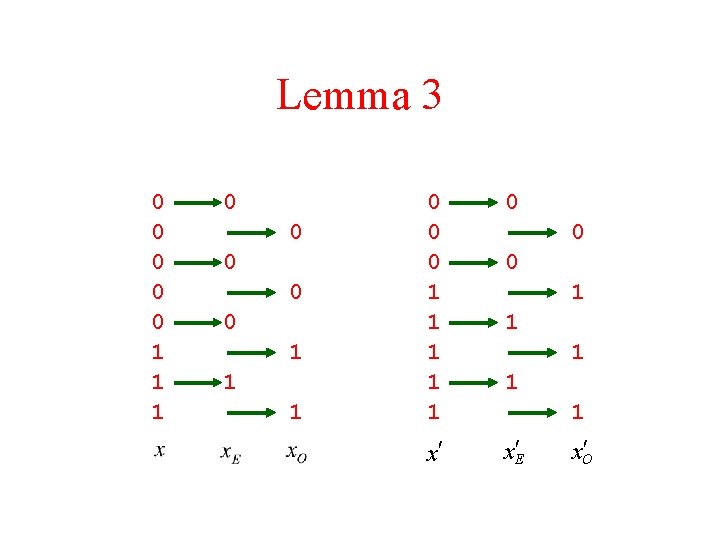
Lemma 3 0 0 0 0 0 1 1 1 0 x¢ x¢E 0 0 1 1 1 x. O¢

Lemma 3 For two sorted sequences and (by Lemma 2) :
![Merge Network sorted Merge[4] Merge Network sorted Merge[4]](http://slidetodoc.com/presentation_image_h2/75af33da1caa26212336f6330f4af402/image-59.jpg)
Merge Network sorted Merge[4]
![Merge Network (pf. ) sorted Merge[4] sorted (by Lemma 1) Merge Network (pf. ) sorted Merge[4] sorted (by Lemma 1)](http://slidetodoc.com/presentation_image_h2/75af33da1caa26212336f6330f4af402/image-60.jpg)
Merge Network (pf. ) sorted Merge[4] sorted (by Lemma 1)
![Merge Network (pf. ) Merge[4] sorted By Lemma 3 and differ by at most Merge Network (pf. ) Merge[4] sorted By Lemma 3 and differ by at most](http://slidetodoc.com/presentation_image_h2/75af33da1caa26212336f6330f4af402/image-61.jpg)
Merge Network (pf. ) Merge[4] sorted By Lemma 3 and differ by at most 1
![Merge Network (pf. ) Merge[4] By Lemma 3 and differ by at most 1 Merge Network (pf. ) Merge[4] By Lemma 3 and differ by at most 1](http://slidetodoc.com/presentation_image_h2/75af33da1caa26212336f6330f4af402/image-62.jpg)
Merge Network (pf. ) Merge[4] By Lemma 3 and differ by at most 1 sorted Merge[4]
![Merge Network (pf. ) 0 0 Merge[4] 1 1 By Lemma 3 and differ Merge Network (pf. ) 0 0 Merge[4] 1 1 By Lemma 3 and differ](http://slidetodoc.com/presentation_image_h2/75af33da1caa26212336f6330f4af402/image-63.jpg)
Merge Network (pf. ) 0 0 Merge[4] 1 1 By Lemma 3 and differ by at most 1 0 0 Merge[4] 0 1 0 0 0 1 1 1
![Batcher Sorting Network Sort[4] Merge[8] Sort[4] sorted Batcher Sorting Network Sort[4] Merge[8] Sort[4] sorted](http://slidetodoc.com/presentation_image_h2/75af33da1caa26212336f6330f4af402/image-64.jpg)
Batcher Sorting Network Sort[4] Merge[8] Sort[4] sorted
![Batcher Sorting Network, n = 4 Sort[2] Merge[4] Batcher Sorting Network, n = 4 Sort[2] Merge[4]](http://slidetodoc.com/presentation_image_h2/75af33da1caa26212336f6330f4af402/image-65.jpg)
Batcher Sorting Network, n = 4 Sort[2] Merge[4]
![Sort[4] Batcher Sorting Network, n = 8 Merge[8] Sort[4] Batcher Sorting Network, n = 8 Merge[8]](http://slidetodoc.com/presentation_image_h2/75af33da1caa26212336f6330f4af402/image-66.jpg)
Sort[4] Batcher Sorting Network, n = 8 Merge[8]

Sorting Networks AKS (Ajtai, Komlós, Szemerédi) Network: based on expander graphs. AKS (Chvátal) AKS better for Batcher
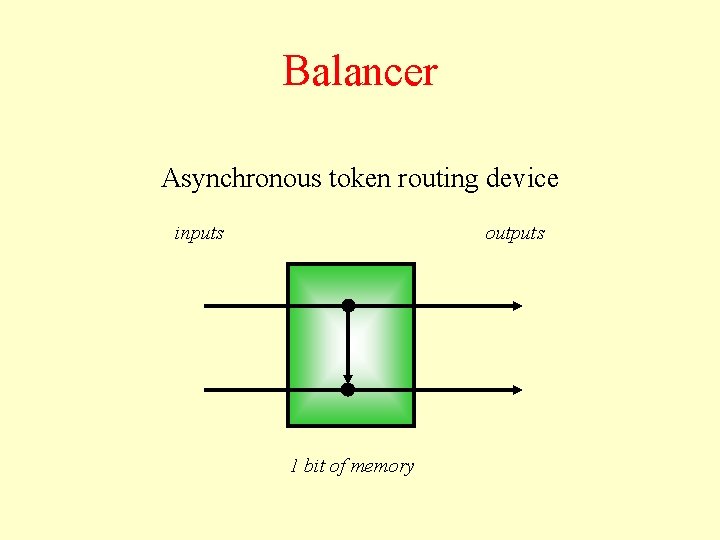
Balancer Asynchronous token routing device inputs outputs 1 bit of memory
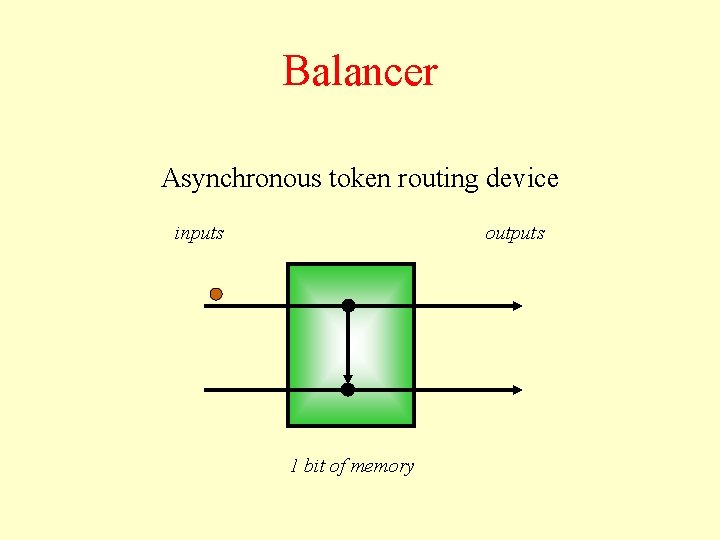
Balancer Asynchronous token routing device inputs outputs 1 bit of memory
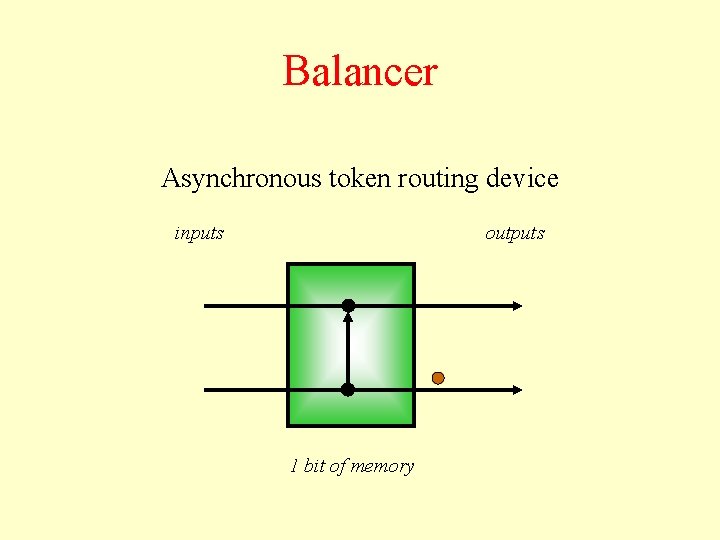
Balancer Asynchronous token routing device inputs outputs 1 bit of memory
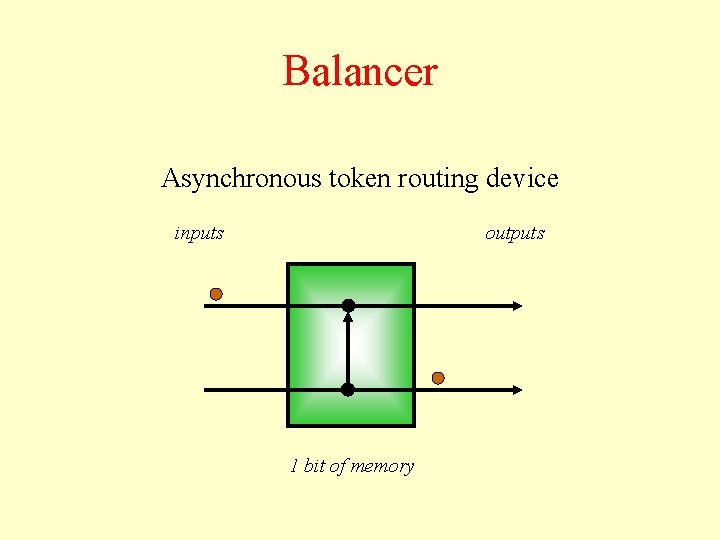
Balancer Asynchronous token routing device inputs outputs 1 bit of memory
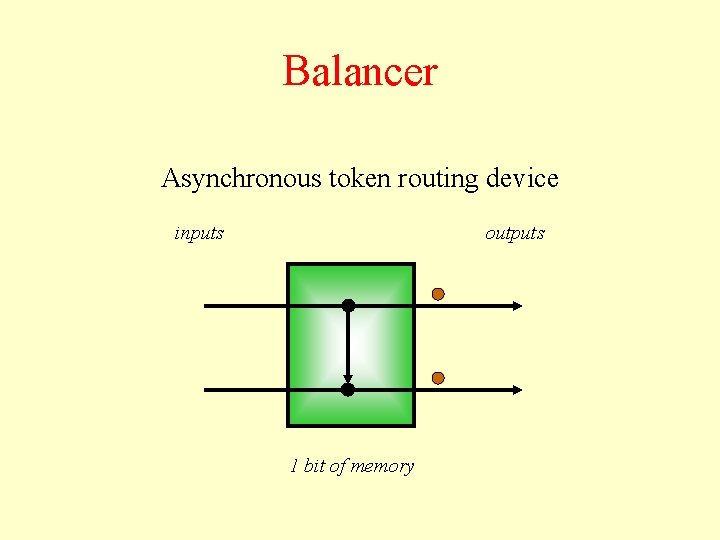
Balancer Asynchronous token routing device inputs outputs 1 bit of memory
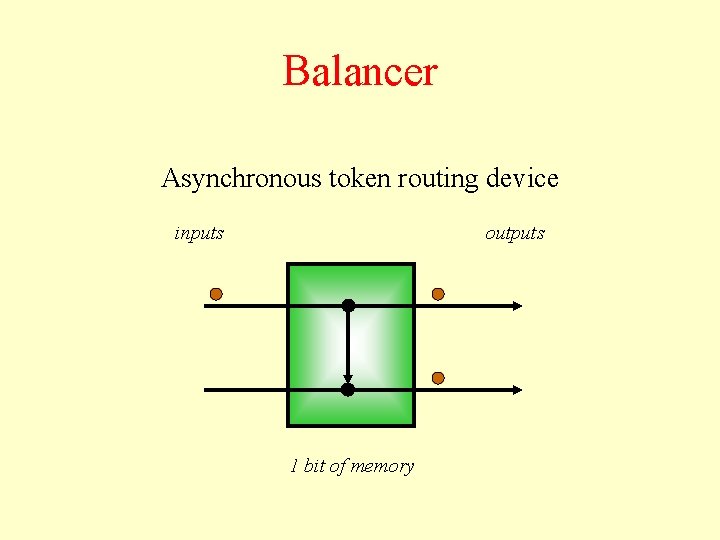
Balancer Asynchronous token routing device inputs outputs 1 bit of memory
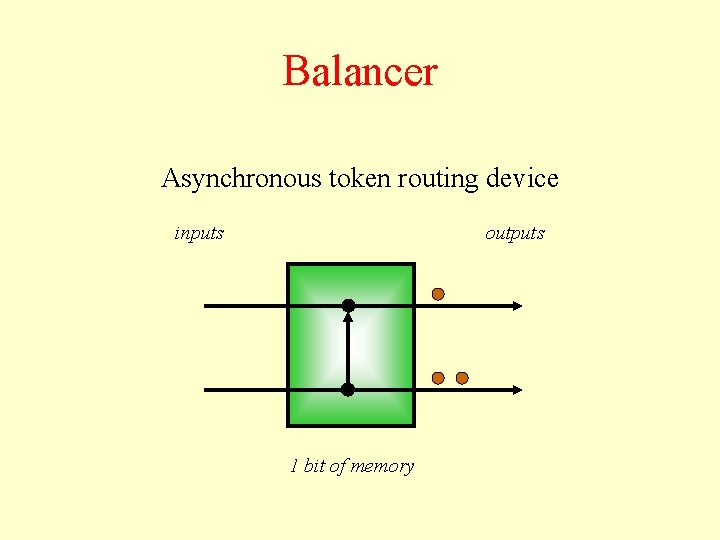
Balancer Asynchronous token routing device inputs outputs 1 bit of memory
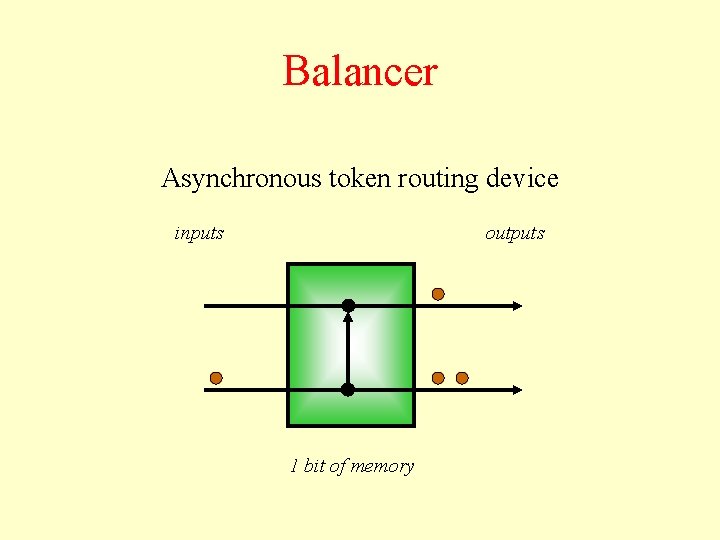
Balancer Asynchronous token routing device inputs outputs 1 bit of memory
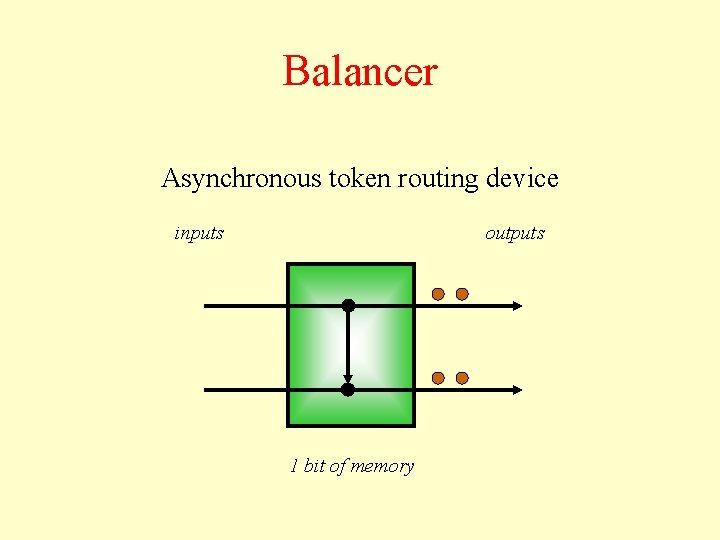
Balancer Asynchronous token routing device inputs outputs 1 bit of memory
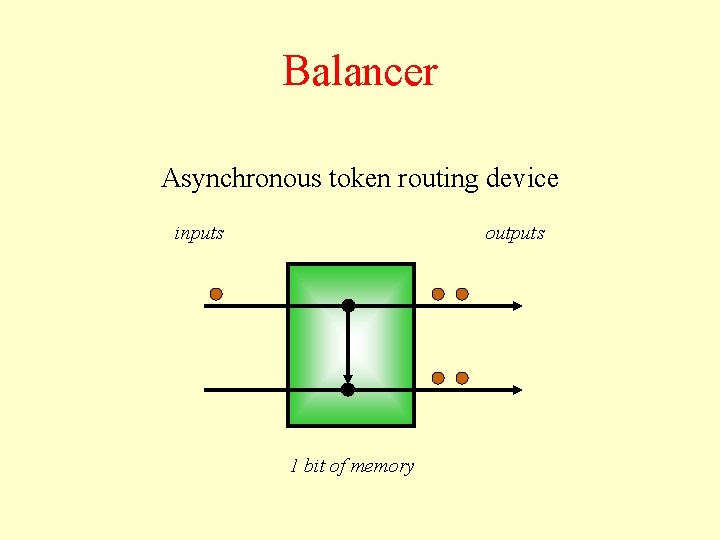
Balancer Asynchronous token routing device inputs outputs 1 bit of memory
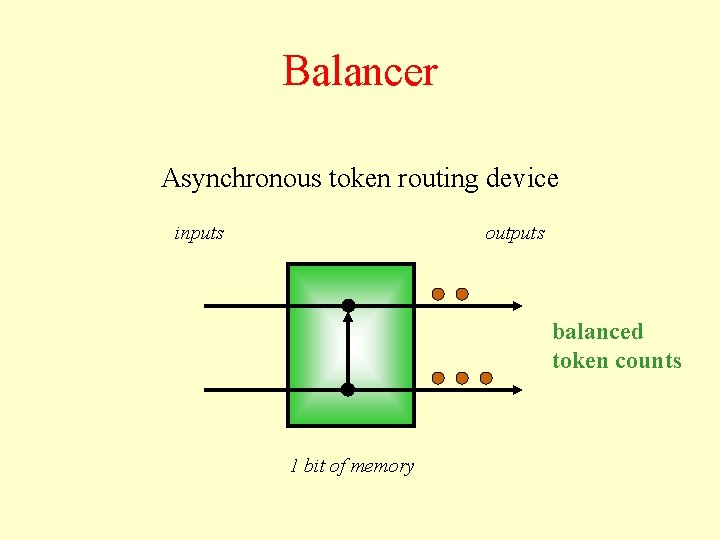
Balancer Asynchronous token routing device inputs outputs balanced token counts 1 bit of memory
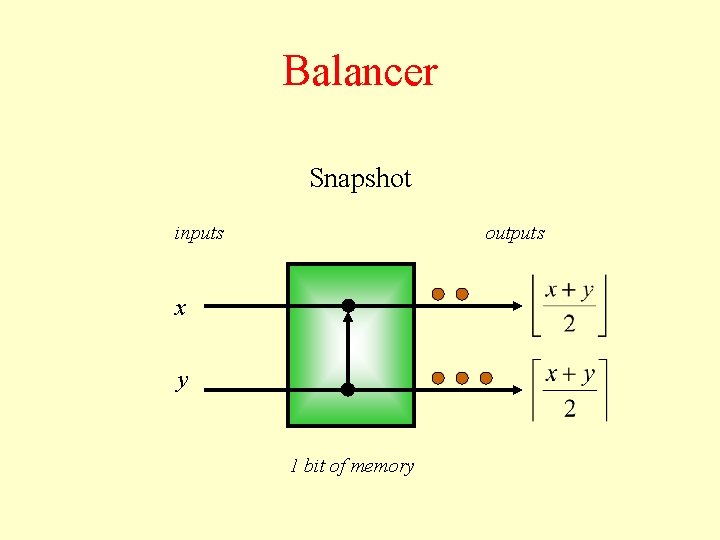
Balancer Snapshot inputs outputs x y 1 bit of memory
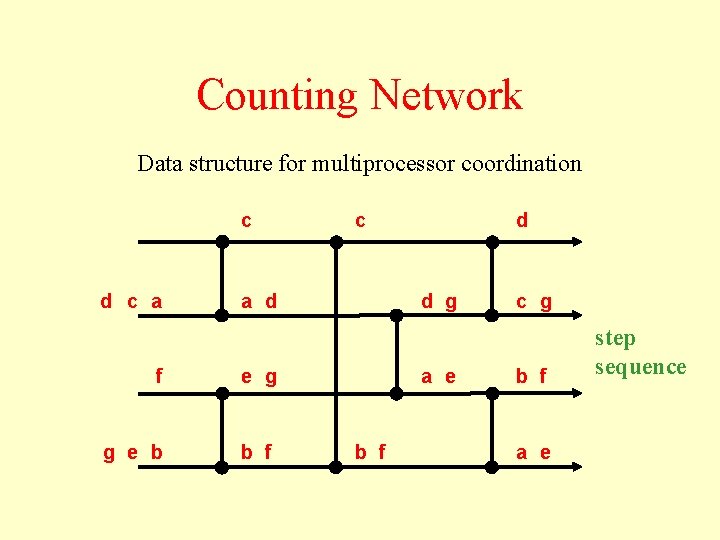
Counting Network Data structure for multiprocessor coordination c d c a d f e g g e b b f d d g a e b f c g b f a e step sequence
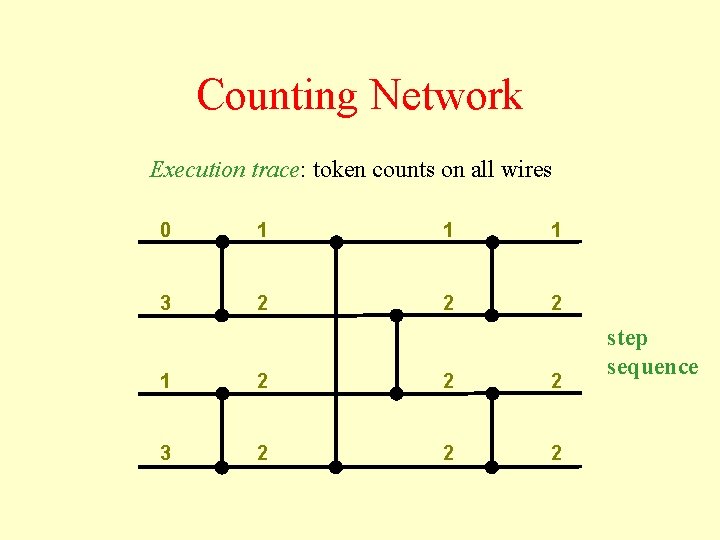
Counting Network Execution trace: token counts on all wires 0 1 1 1 3 2 2 2 1 2 2 2 3 2 2 2 step sequence

Counting Network Tokens are assigned value based on the output wire number. 4, 8, 12, 16, . . . Counting Network 3, 7, 11, 15, . . . Advantages 2, 6, 10, 14, . . . • High throughput • Low contention 1, 5, 9, 13, . . .
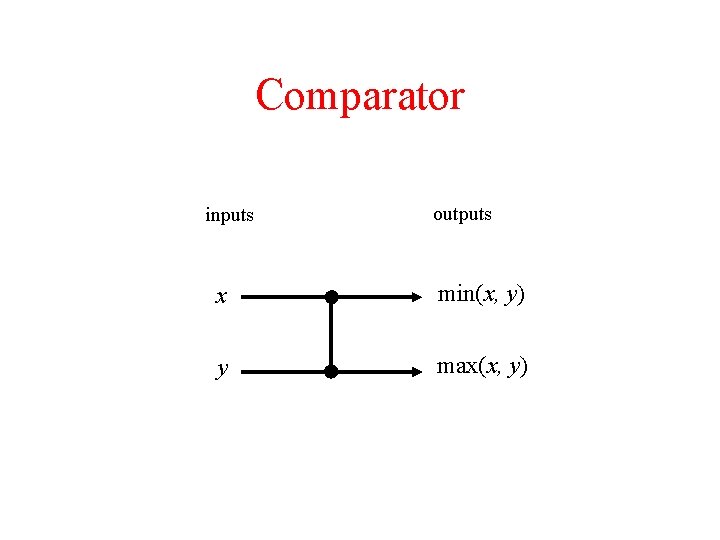
Comparator inputs outputs x min(x, y) y max(x, y)
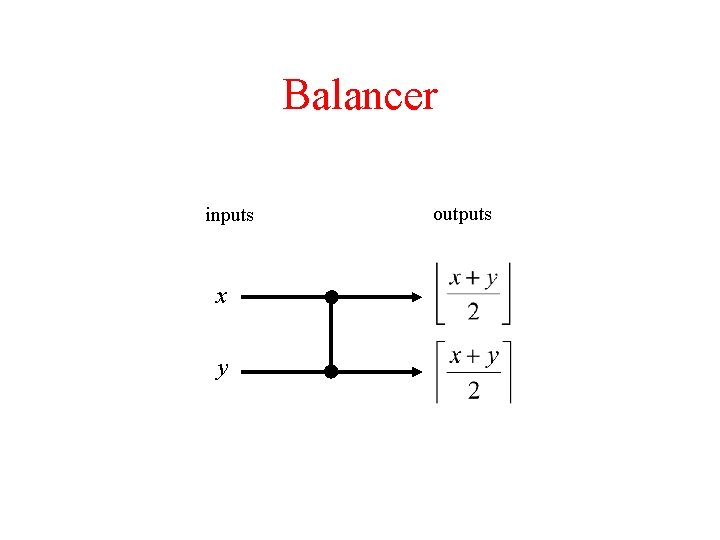
Balancer inputs x y outputs
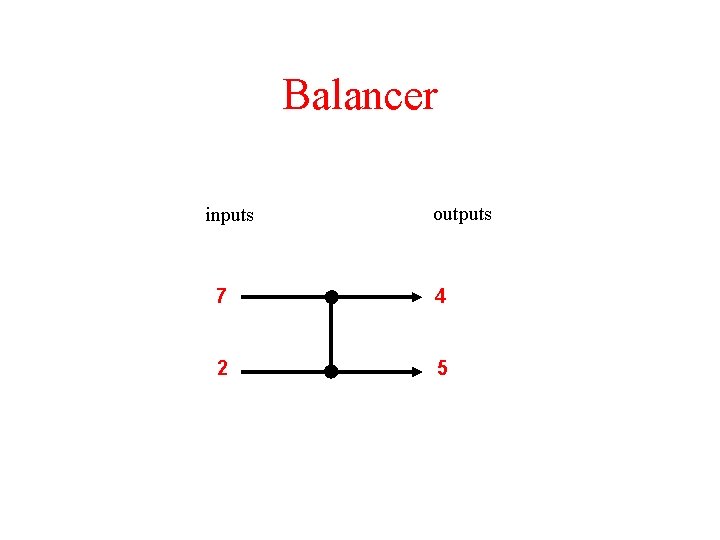
Balancer inputs outputs 7 4 2 5
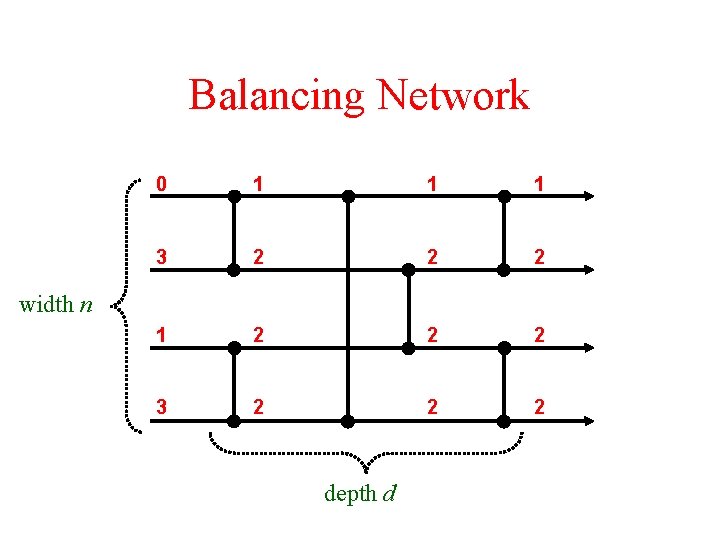
Balancing Network 0 1 1 1 3 2 2 2 1 2 2 2 3 2 2 2 width n depth d
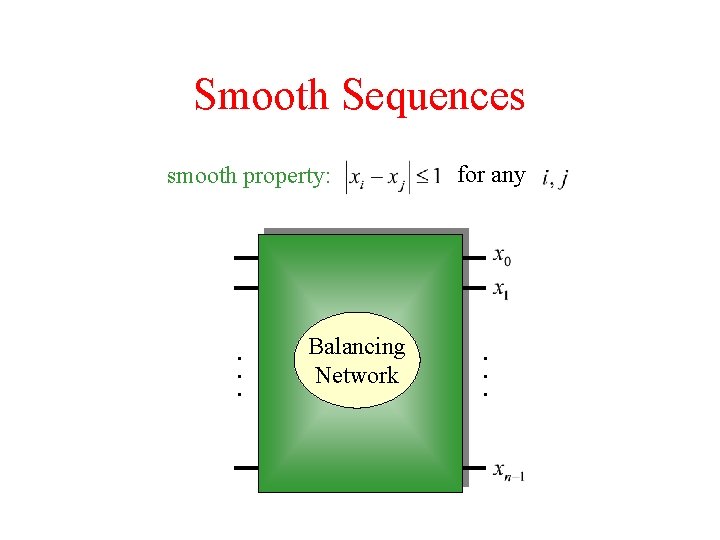
Smooth Sequences smooth property: . . . Balancing Network for any . . .
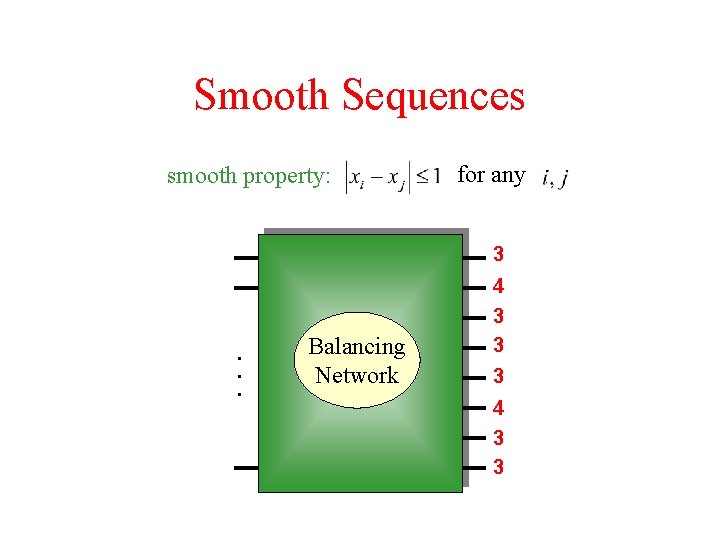
Smooth Sequences smooth property: for any 3 . . . Balancing Network 4 3 3 3 4 3 3
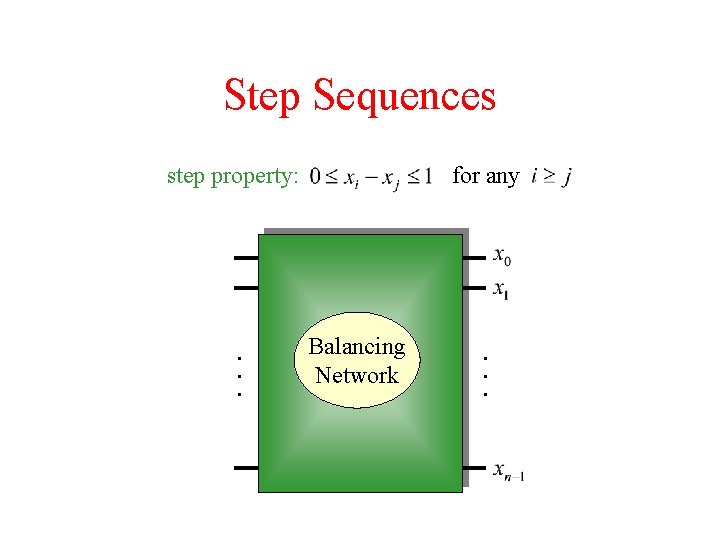
Step Sequences step property: . . . for any Balancing Network . . .
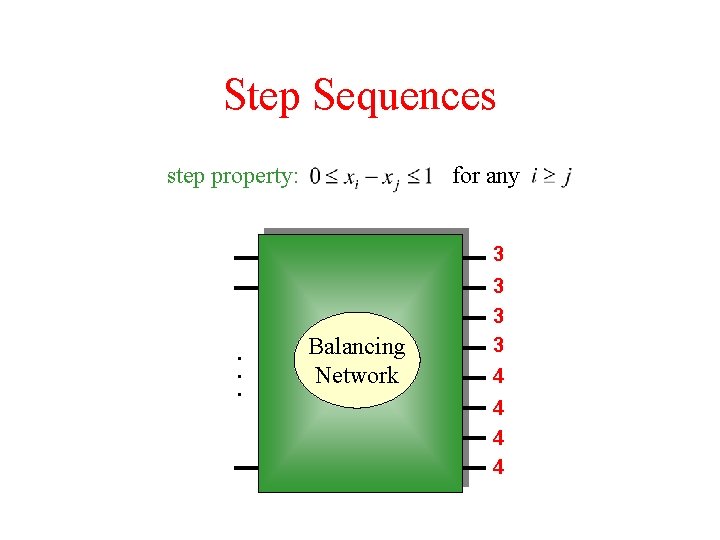
Step Sequences step property: for any 3 . . . Balancing Network 3 3 3 4 4
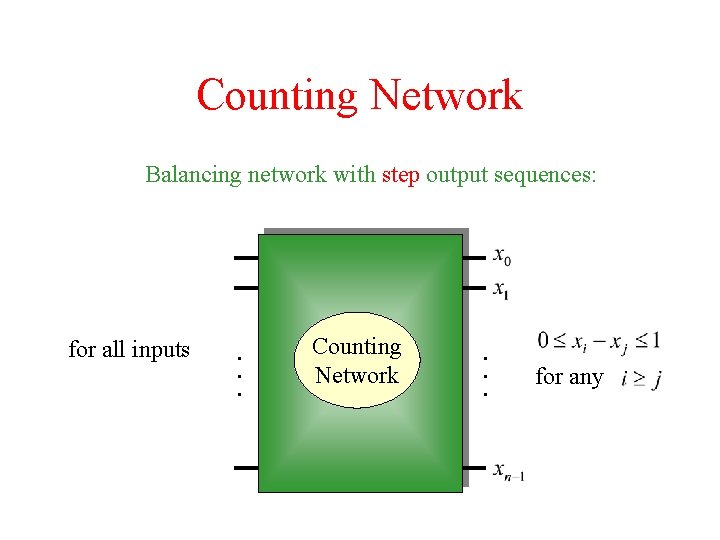
Counting Network Balancing network with step output sequences: for all inputs . . . Counting Network . . . for any

Sorting vs. Counting ? Counts . . . Balancing Network Sorts . . . isomorphic . . . Comparison Network . . .

Sorting vs. Counting ? Counts . . . Balancing Network Sorts . . . isomorphic . . . Comparison Network . . .

Sorting vs. Counting ? Counts . . . Balancing Network Sorts . . . isomorphic . . . Comparison Network . . .

Sorting vs. Counting Theorem If a balancing network counts, then its isomorphic comparison network sorts, but not vice-versa.
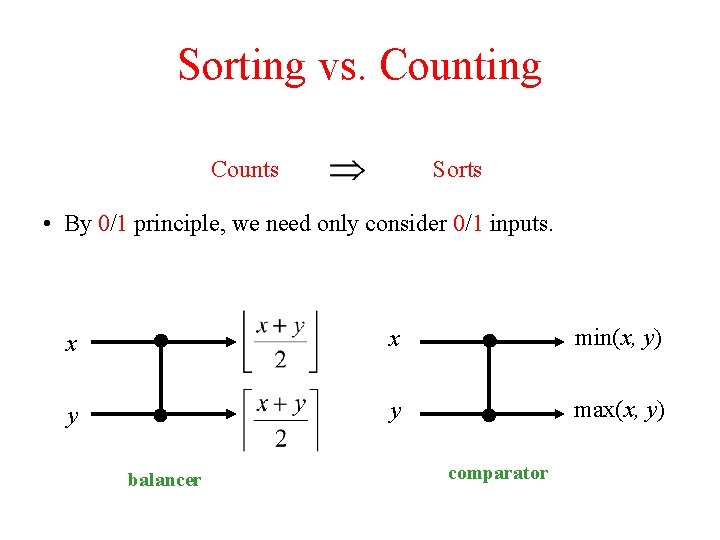
Sorting vs. Counting Counts Sorts • By 0/1 principle, we need only consider 0/1 inputs. x x min(x, y) y y max(x, y) balancer comparator
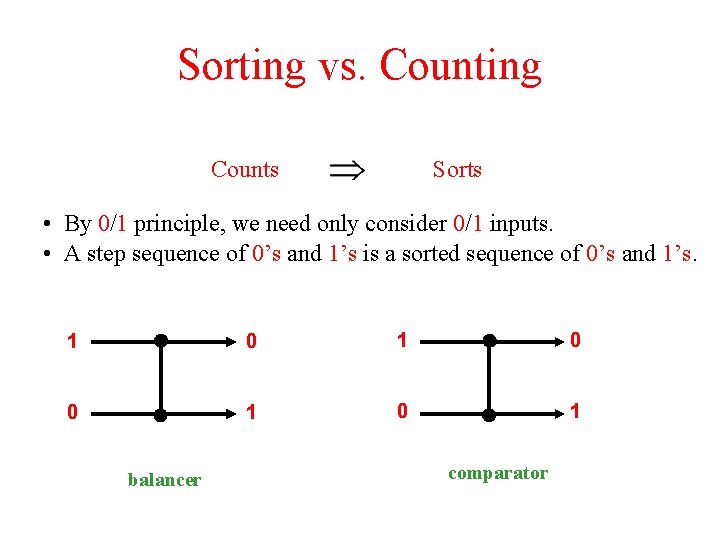
Sorting vs. Counting Counts Sorts • By 0/1 principle, we need only consider 0/1 inputs. • A step sequence of 0’s and 1’s is a sorted sequence of 0’s and 1’s. 1 0 0 1 balancer comparator
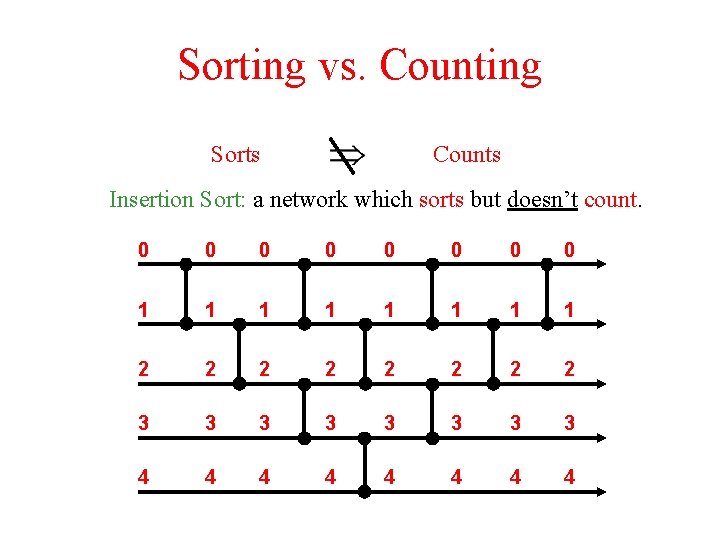
Sorting vs. Counting Sorts Counts Insertion Sort: a network which sorts but doesn’t count. 0 0 0 0 1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4
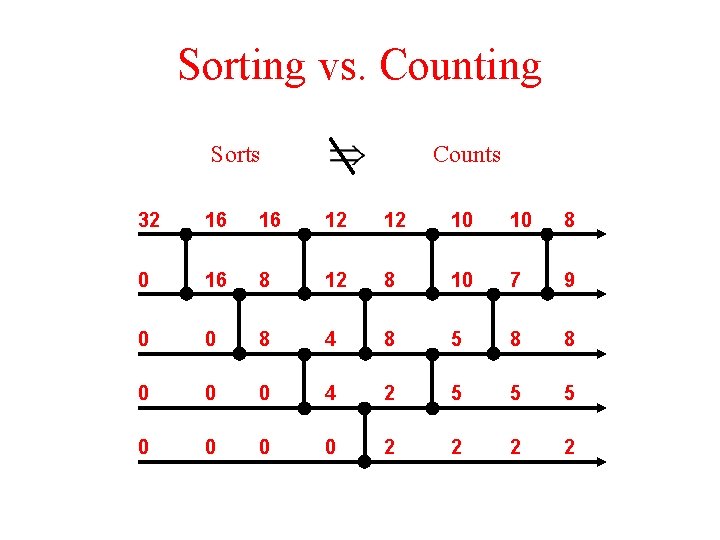
Sorting vs. Counting Sorts Counts 32 16 16 12 12 10 10 8 0 16 8 12 8 10 7 9 0 0 8 4 8 5 8 8 0 0 0 4 2 5 5 5 0 0 2 2
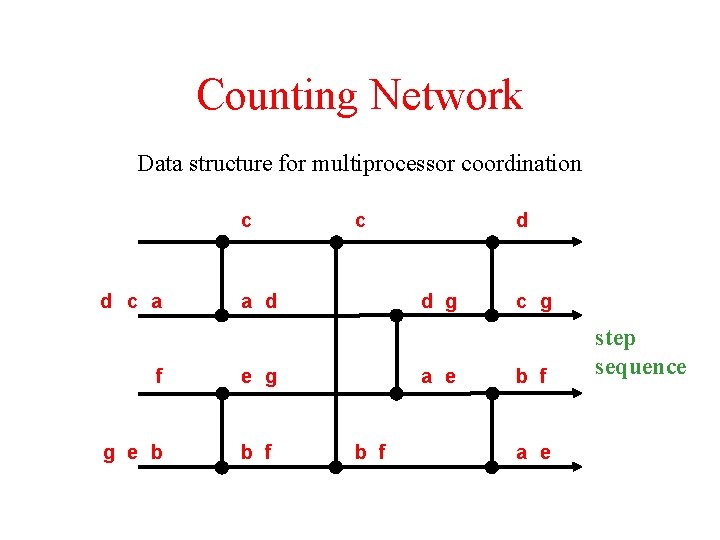
Counting Network Data structure for multiprocessor coordination c d c a d f e g g e b b f d d g a e b f c g b f a e step sequence
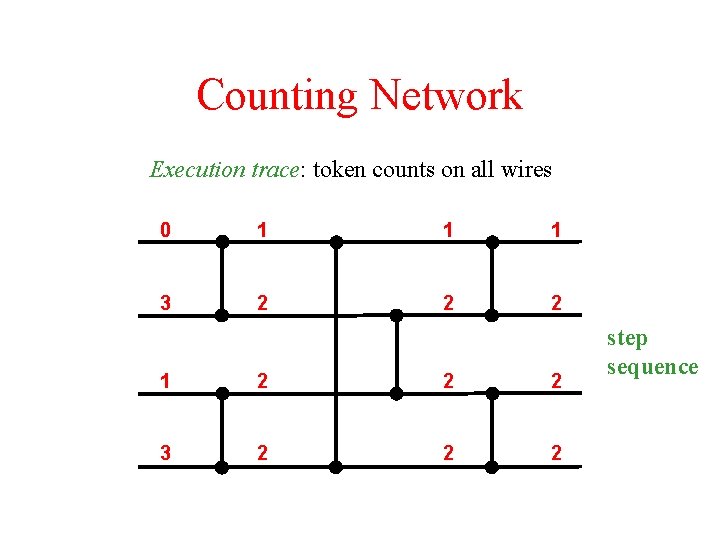
Counting Network Execution trace: token counts on all wires 0 1 1 1 3 2 2 2 1 2 2 2 3 2 2 2 step sequence

Counting Network Tokens are assigned value based on the output wire number. 4, 8, 12, 16, . . . Counting Network 3, 7, 11, 15, . . . Advantages 2, 6, 10, 14, . . . • High throughput • Low contention 1, 5, 9, 13, . . .
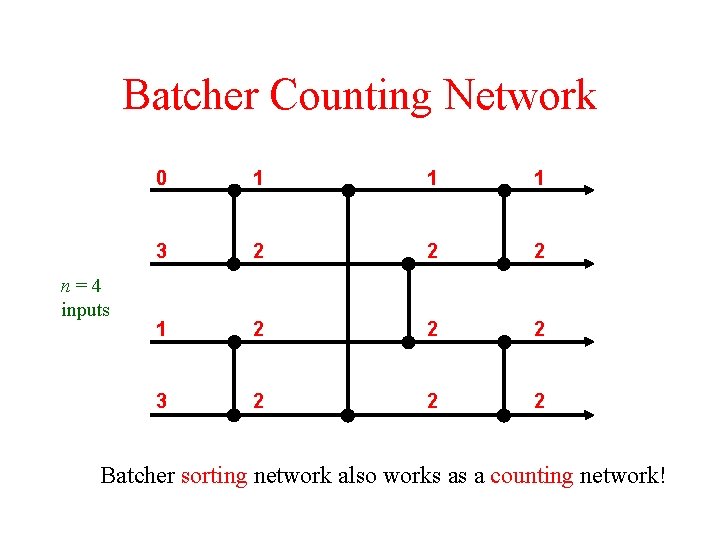
Batcher Counting Network n=4 inputs 0 1 1 1 3 2 2 2 1 2 2 2 3 2 2 2 Batcher sorting network also works as a counting network!
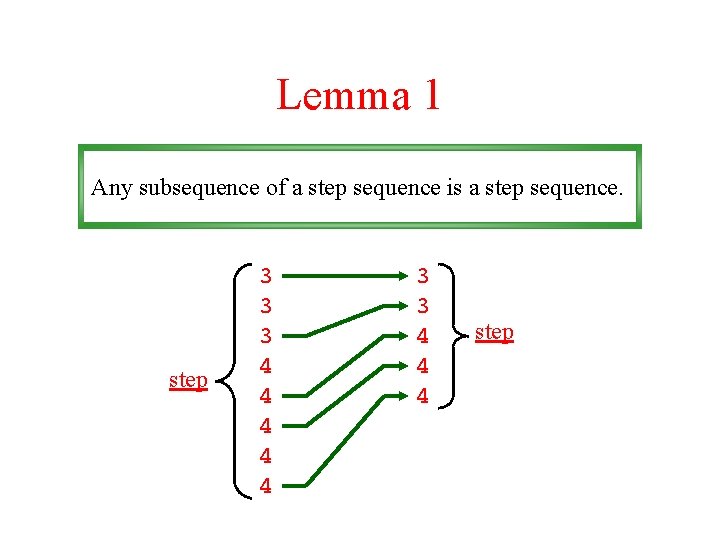
Lemma 1 Any subsequence of a step sequence is a step sequence. step 3 3 3 4 4 4 step

Lemma 2 For a step sequence, the sum of the even subsequence is either equal to, or one less than, the sum of the odd subsequence. step 3 3 3 4 4 4 4 4 even odd Sum of even subseq. : 3+3+4+4=14 Sum of odd subseq. : 3+4+4+4=15

Lemma 3 For two step sequences and : denotes the sum of denotes the even subsequence of denotes the odd subsequence of Follows from: (by Lemma 2)
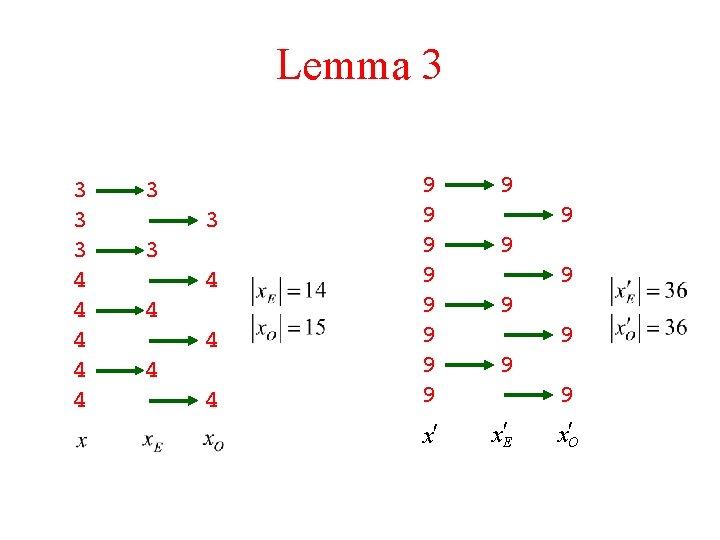
Lemma 3 3 4 4 4 3 3 3 4 4 4 9 9 9 9 9 x¢ x¢E 9 9 9 9 x. O¢
![Merge Network step Merge[4] Merge Network step Merge[4]](http://slidetodoc.com/presentation_image_h2/75af33da1caa26212336f6330f4af402/image-108.jpg)
Merge Network step Merge[4]
![Merge Network (pf. ) step Merge[4] step Merge Network (pf. ) step Merge[4] step](http://slidetodoc.com/presentation_image_h2/75af33da1caa26212336f6330f4af402/image-109.jpg)
Merge Network (pf. ) step Merge[4] step
![Merge Network (pf. ) Merge[4] step By Lemma 3 and differ by at most Merge Network (pf. ) Merge[4] step By Lemma 3 and differ by at most](http://slidetodoc.com/presentation_image_h2/75af33da1caa26212336f6330f4af402/image-110.jpg)
Merge Network (pf. ) Merge[4] step By Lemma 3 and differ by at most 1
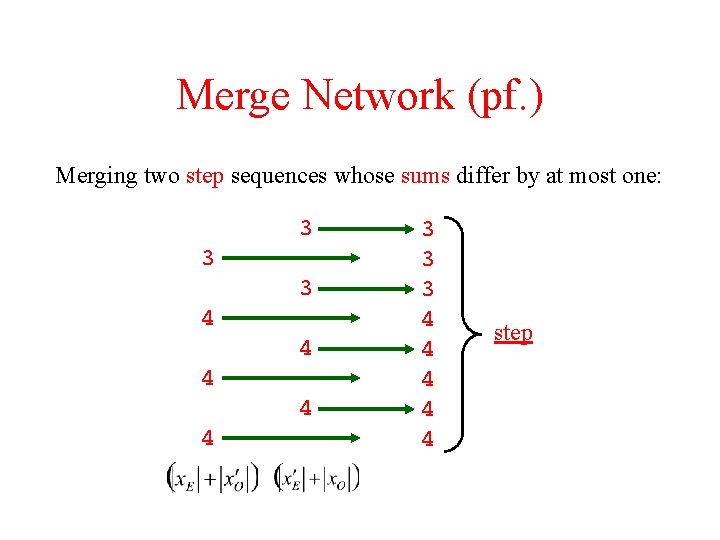
Merge Network (pf. ) Merging two step sequences whose sums differ by at most one: 3 3 3 4 4 4 4 4 step

Merge Network (pf. ) Merging two step sequences whose sums differ by at most one: 3 3 4 3 4 4 4 4 not quite step
![Merge Network (pf. ) Merge[4] step Merge[4] Merge Network (pf. ) Merge[4] step Merge[4]](http://slidetodoc.com/presentation_image_h2/75af33da1caa26212336f6330f4af402/image-113.jpg)
Merge Network (pf. ) Merge[4] step Merge[4]
![Batcher Counting Network Count[4] Merge[8] Count[4] step Batcher Counting Network Count[4] Merge[8] Count[4] step](http://slidetodoc.com/presentation_image_h2/75af33da1caa26212336f6330f4af402/image-114.jpg)
Batcher Counting Network Count[4] Merge[8] Count[4] step

Verifying that a Network Counts Theorem A balancing network with m balancers is a counting network if and only if it satisfies the step property for all input sequences with sum.
- Slides: 115