Comparing Two Motions Jehee Lee Seoul National University

Comparing Two Motions Jehee Lee Seoul National University

Distance Metric for Motion Sequences • How can we measure the difference between two stylistic walking motions? • How do we represent motion sequences? – Rotation/orientation makes problems • We do we compare two time-series data? – What if the duration of one series differ from the other?

Affine Geometry Jehee Lee Seoul National University

Geometric Programming • A way of handling geometric entities such as vectors, points, and transforms. • Traditionally, computer graphics packages are implemented using homogeneous coordinates. • We will review affine geometry and coordinate-invariant geometric programming.

Example of coordinate-dependence Point p Point q • What is the “sum” of these two positions ?

If you assume coordinates, … p = (x 1, y 1) q = (x 2, y 2) • The sum is (x 1+x 2, y 1+y 2) – Is it correct ? – Is it geometrically meaningful ?

If you assume coordinates, … p = (x 1, y 1) (x 1+x 2, y 1+y 2) q = (x 2, y 2) Origin • Vector sum – (x 1, y 1) and (x 2, y 2) are considered as vectors from the origin to p and q, respectively.

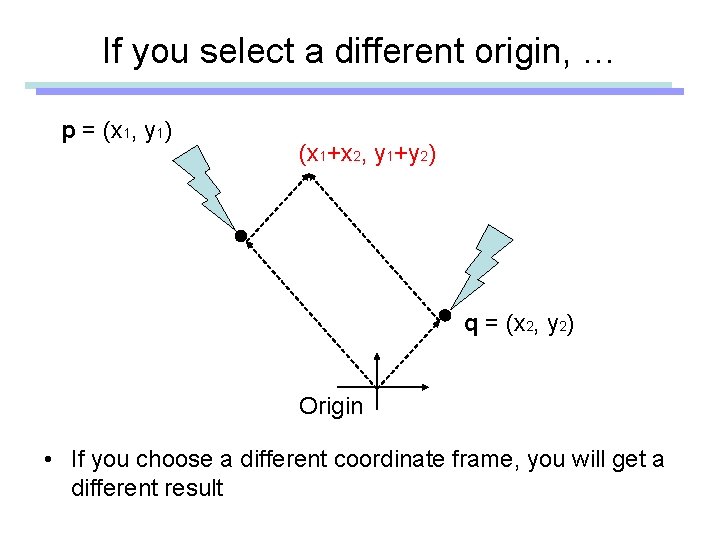
If you select a different origin, … p = (x 1, y 1) (x 1+x 2, y 1+y 2) q = (x 2, y 2) Origin • If you choose a different coordinate frame, you will get a different result

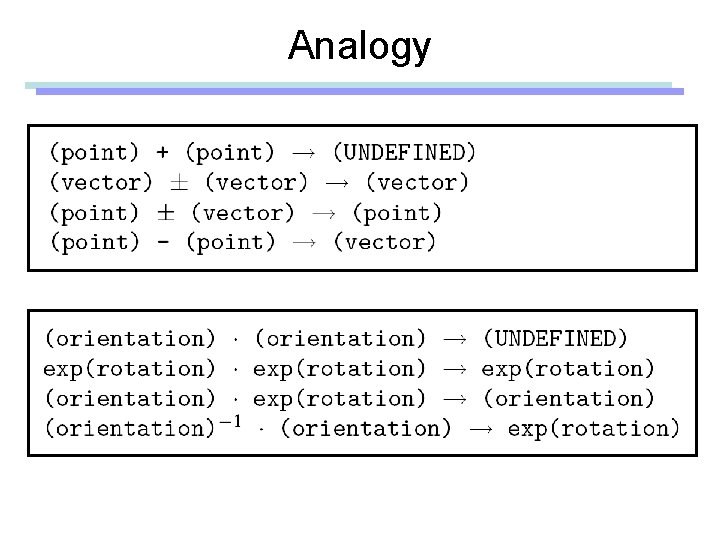
Vector and Affine Spaces • Vector space – Includes vectors and related operations – No points • Affine space – Superset of vector space – Includes vectors, points, and related operations

Points and Vectors vector (p-q) Point q Point p • A point is a position specified with coordinate values. • A vector is specified as the difference between two points. • If an origin is specified, then a point can be represented by a vector from the origin. • But, a point is still not a vector in a coordinate-free point of view.

Vector spaces • A vector space consists of – Set of vectors, together with – Two operations: addition of vectors and multiplication of vectors by scalar numbers • A linear combination of vectors is also a vector

Affine Spaces • An affine space consists of – Set of points, an associated vector space, and – Two operations: the difference between two points and the addition of a vector to a point

Coordinate-Invariant Geometric Operations • • • Addition Subtraction Scalar multiplication Linear combination Affine combination

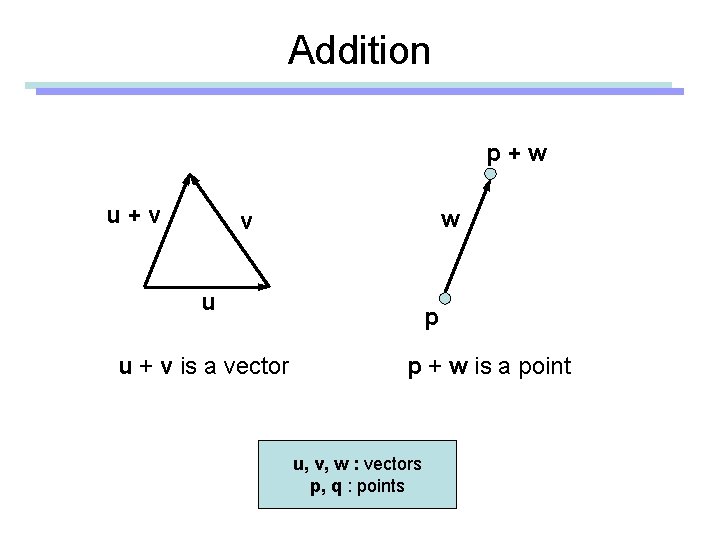
Addition p+w u+v w v u u + v is a vector p p + w is a point u, v, w : vectors p, q : points

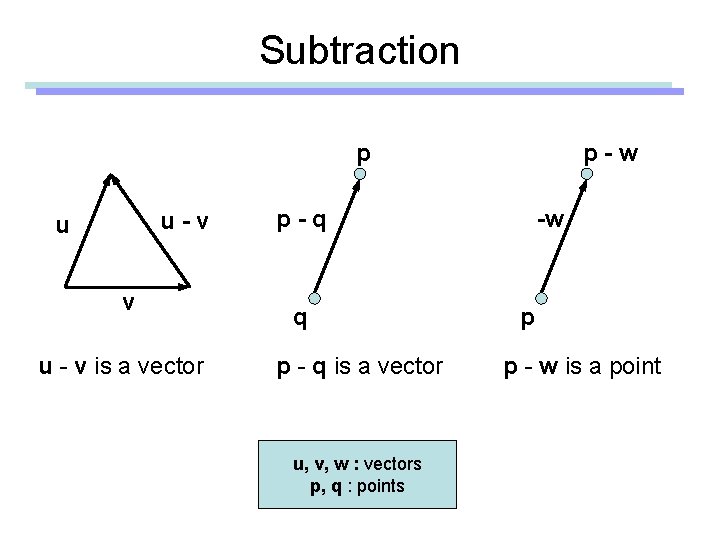
Subtraction p u-v u - v is a vector p-w p-q q p - q is a vector u, v, w : vectors p, q : points -w p p - w is a point

Scalar Multiplication scalar • vector = vector 1 • point = point 0 • point = vector c • point = (undefined) if (c≠ 0, 1)

Linear Combination • A linear space is spanned by a set of bases – Any vector in the space can be represented as a linear combination of bases

Affine Combination

Example • (p + q) / 2 : midpoint of line pq • (p + q) / 3 : Can you find a geometric meaning ? • (p + q + r) / 3 : center of gravity of ∆pqr • (p/2 + q/2 – r) : a vector from r to the midpoint of q and p

Summary

Rotation and Orientation: Fundamentals Jehee Lee Seoul National University

What is Rotation ? • Not intuitive – Formal definitions are also confusing • Many different ways to describe – – – Rotation (direction cosine) matrix Euler angles Axis-angle Rotation vector Helical angles Unit quaternions

Orientation vs. Rotation • Rotation – Circular movement • Orientation – The state of being oriented – Given a coordinate system, the orientation of an object can be represented as a rotation from a reference pose

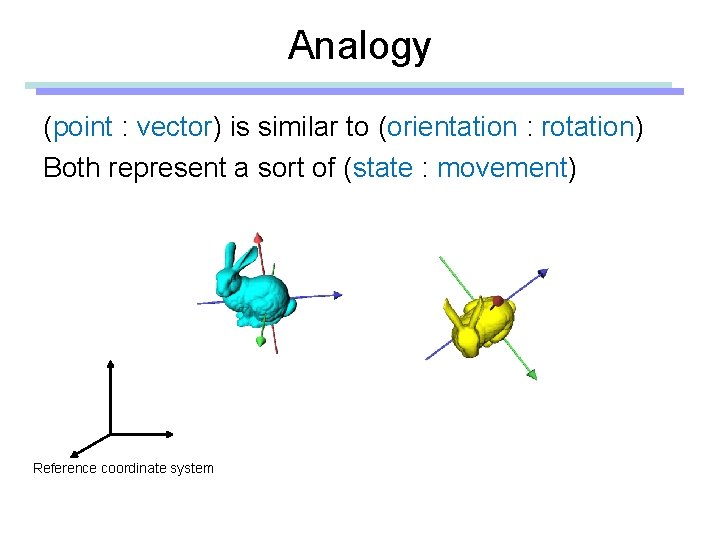
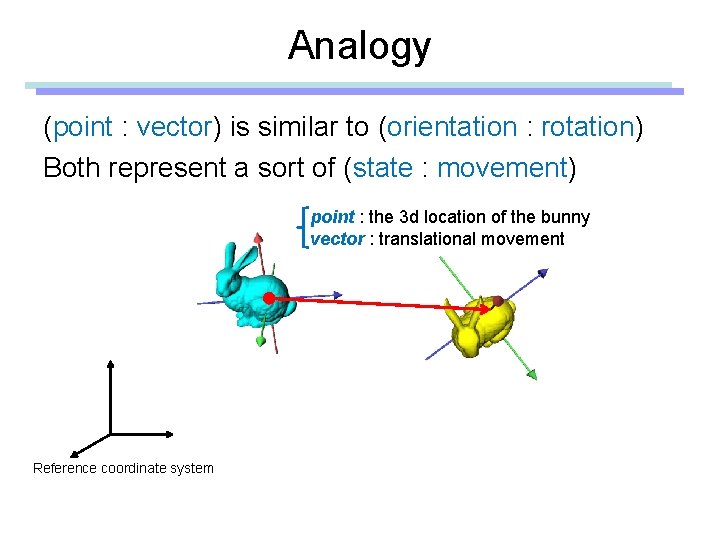
Analogy (point : vector) is similar to (orientation : rotation) Both represent a sort of (state : movement) Reference coordinate system

Analogy (point : vector) is similar to (orientation : rotation) Both represent a sort of (state : movement) point : the 3 d location of the bunny vector : translational movement Reference coordinate system

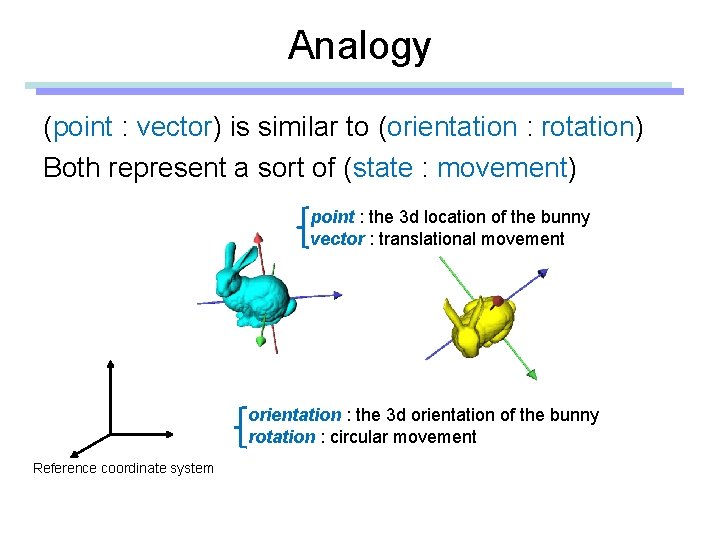
Analogy (point : vector) is similar to (orientation : rotation) Both represent a sort of (state : movement) point : the 3 d location of the bunny vector : translational movement orientation : the 3 d orientation of the bunny rotation : circular movement Reference coordinate system

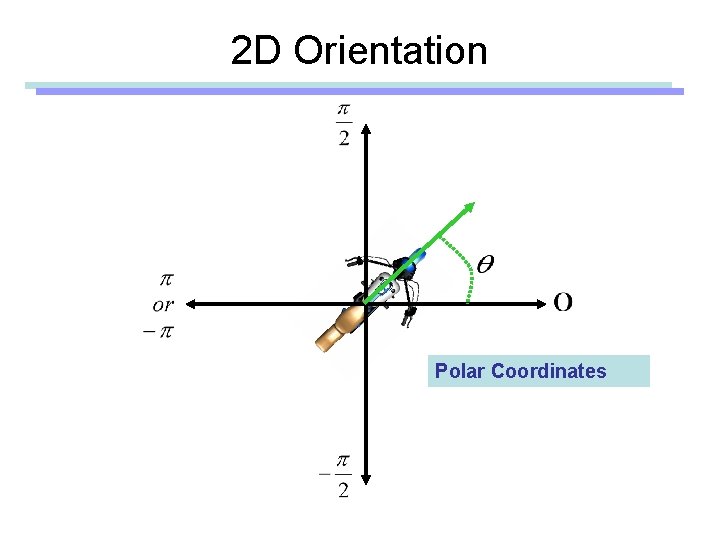
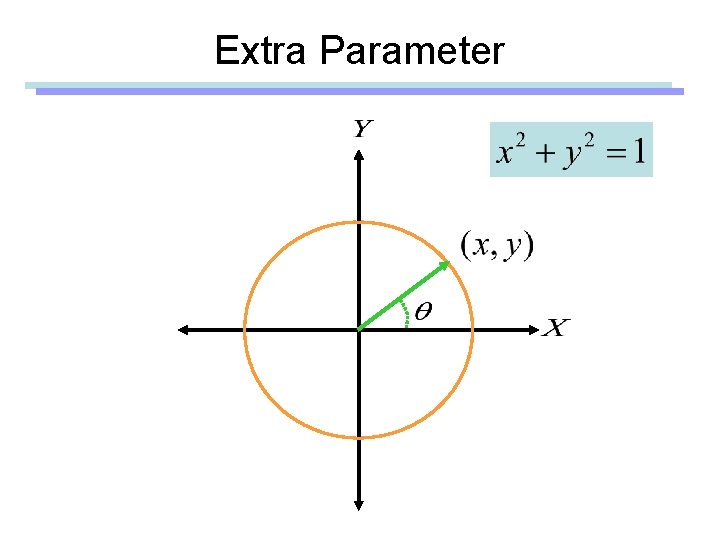
2 D Orientation Polar Coordinates

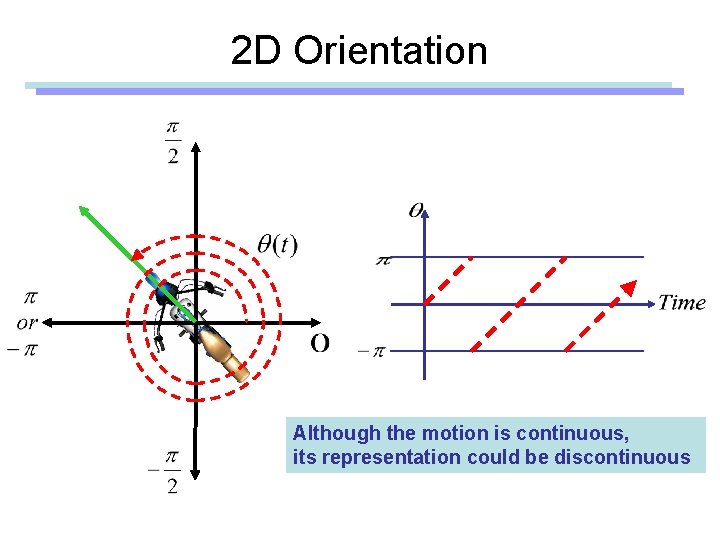
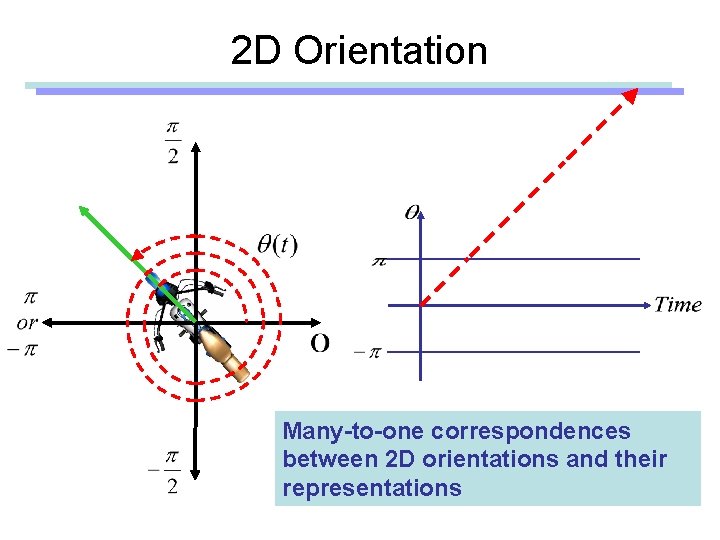
2 D Orientation Although the motion is continuous, its representation could be discontinuous

2 D Orientation Many-to-one correspondences between 2 D orientations and their representations

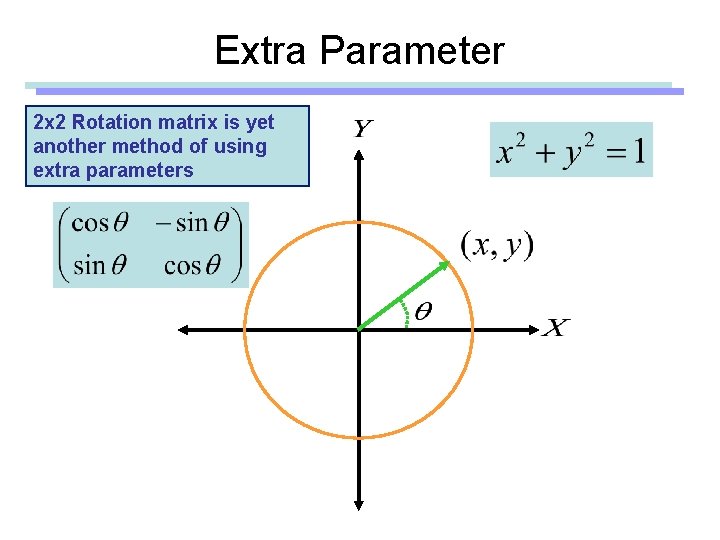
Extra Parameter

Extra Parameter 2 x 2 Rotation matrix is yet another method of using extra parameters

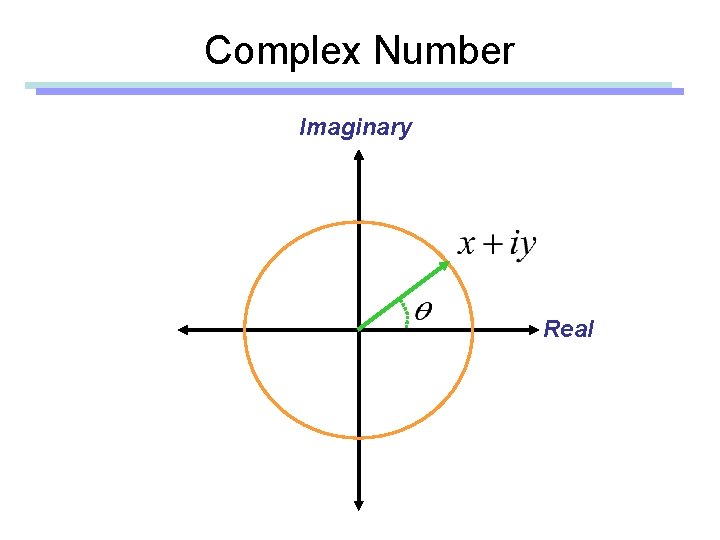
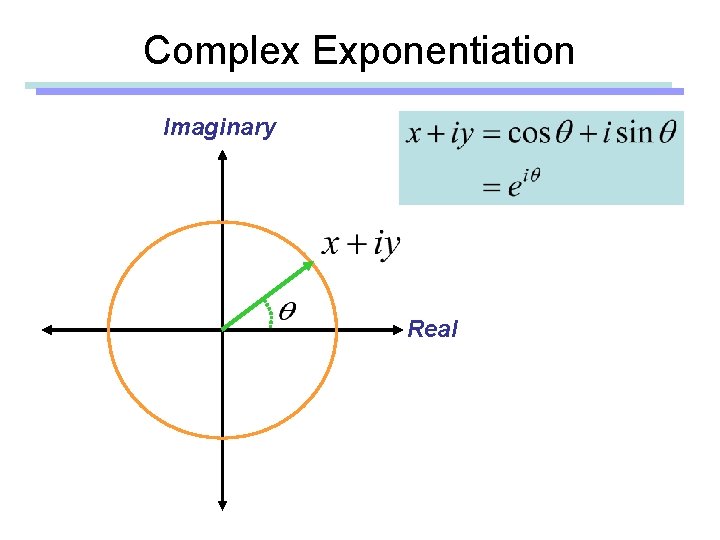
Complex Number Imaginary Real

Complex Exponentiation Imaginary Real

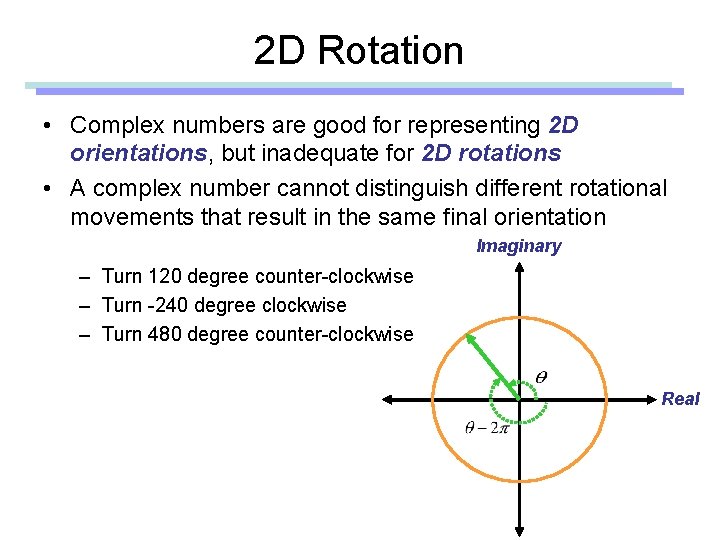
2 D Rotation • Complex numbers are good for representing 2 D orientations, but inadequate for 2 D rotations • A complex number cannot distinguish different rotational movements that result in the same final orientation Imaginary – Turn 120 degree counter-clockwise – Turn -240 degree clockwise – Turn 480 degree counter-clockwise Real

2 D Rotation and Orientation • 2 D Rotation – The consequence of any 2 D rotational movement can be uniquely represented by a turning angle • 2 D Orientation – The non-singular parameterization of 2 D orientations requires extra parameters • Eg) Complex numbers, 2 x 2 rotation matrices

Operations in 2 D • (orientation) : complex number • (rotation) : scalar value • exp(rotation) : complex number

2 D Rotation and Displacement Imaginary Real

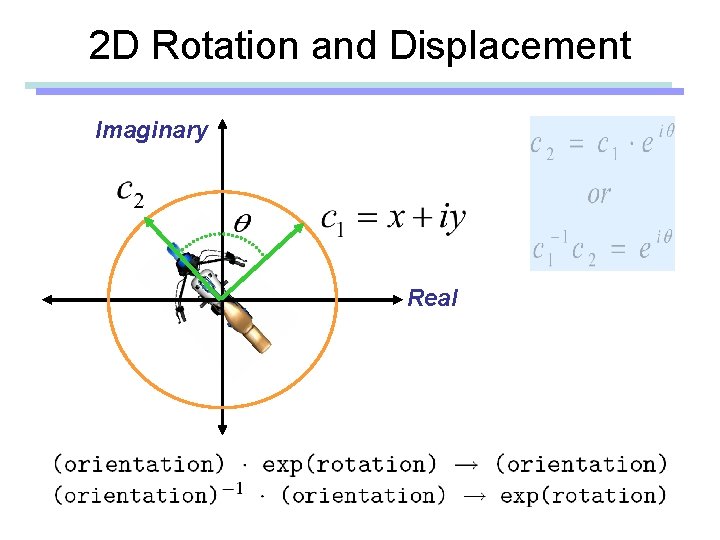
2 D Rotation and Displacement Imaginary Real

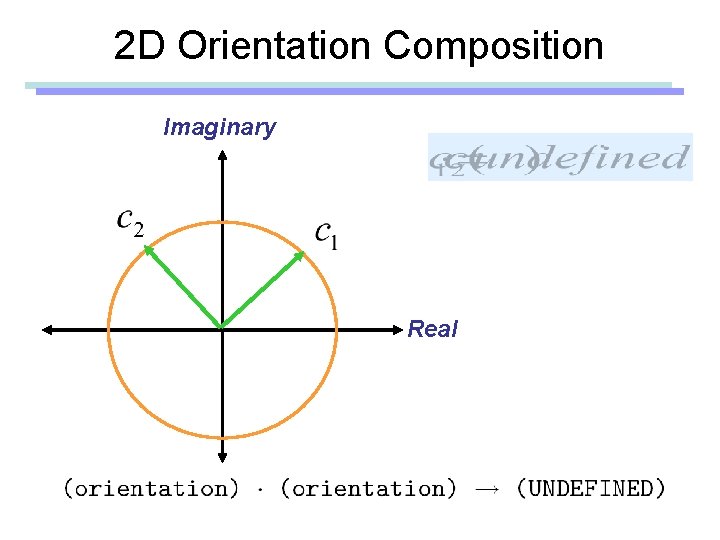
2 D Orientation Composition Imaginary Real

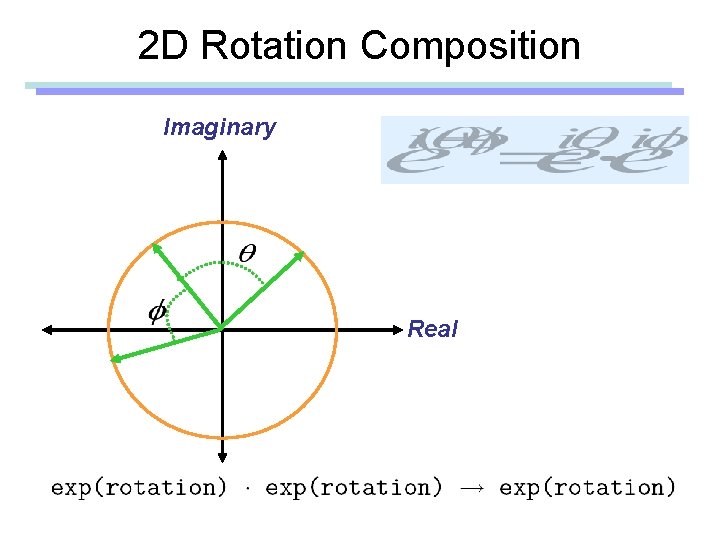
2 D Rotation Composition Imaginary Real

Analogy

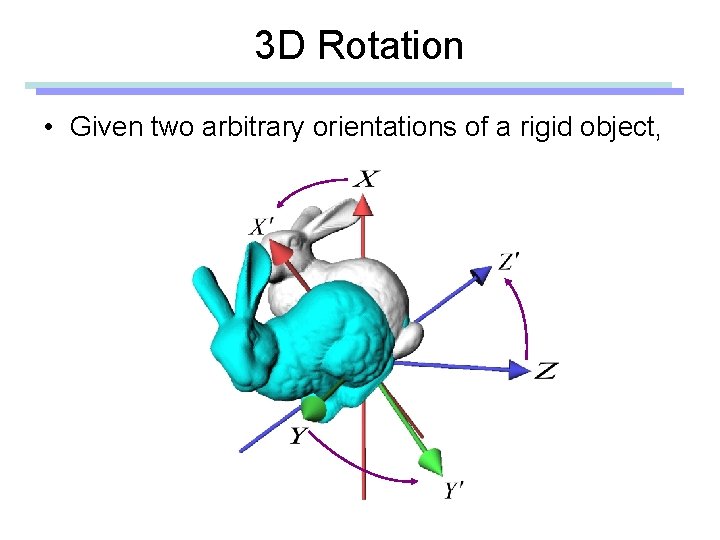
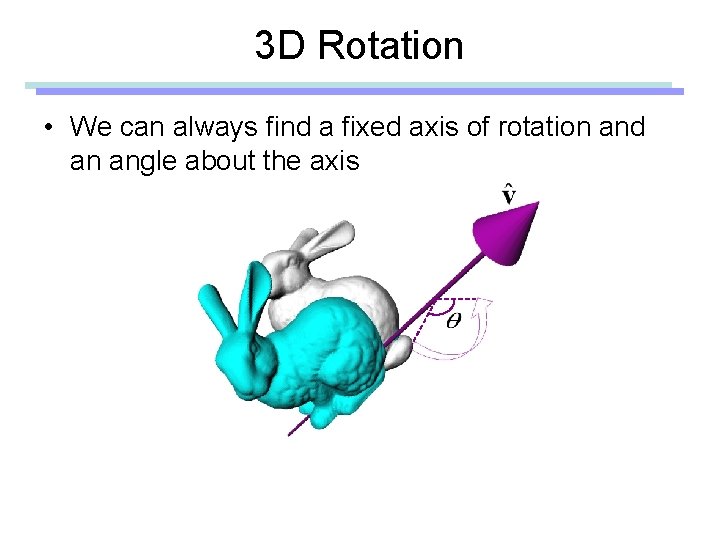
3 D Rotation • Given two arbitrary orientations of a rigid object,

3 D Rotation • We can always find a fixed axis of rotation and an angle about the axis

Euler’s Rotation Theorem The general displacement of a rigid body with one point fixed is a rotation about some axis Leonhard Euler (1707 -1783) In other words, • Arbitrary 3 D rotation equals to one rotation around an axis • Any 3 D rotation leaves one vector unchanged

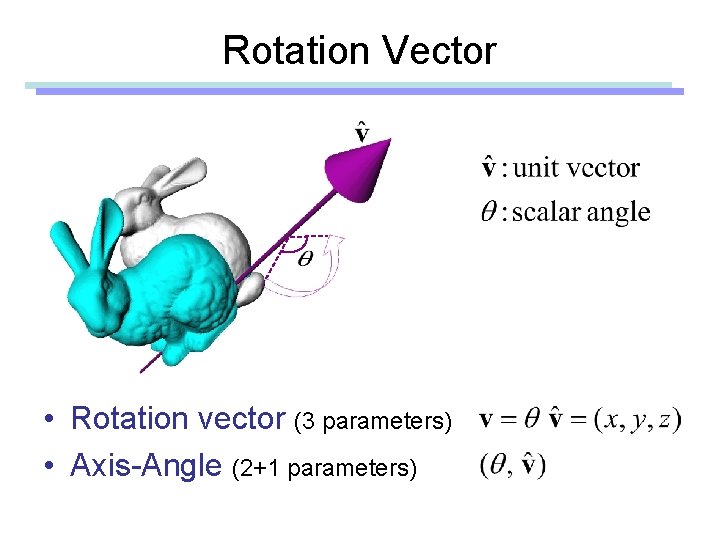
Rotation Vector • Rotation vector (3 parameters) • Axis-Angle (2+1 parameters)

3 D Orientation • Unhappy with three parameters – Euler angles • Discontinuity (or many-to-one correspondences) • Gimble lock – Rotation vector (a. k. a Axis/Angle) • Discontinuity (or many-to-one correspondences)

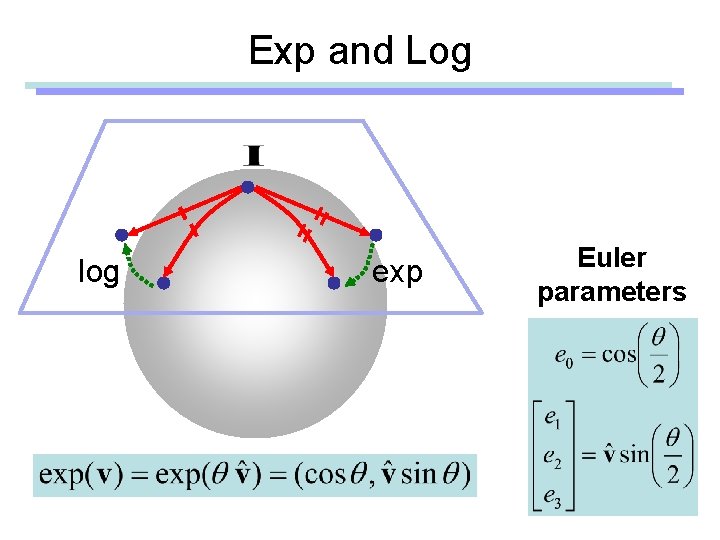
Using an Extra Parameter • Euler parameters

Quaternions • William Rowan Hamilton (1805 -1865) – Algebraic couples (complex number) 1833 where

Quaternions • William Rowan Hamilton (1805 -1865) – Algebraic couples (complex number) 1833 where – Quaternions 1843 where

Unit Quaternions • Unit quaternions represent 3 D rotations

Rotation about an Arbitrary Axis • Rotation about axis by angle where Purely Imaginary Quaternion

Unit Quaternion Algebra • Identity • Multiplication • Inverse – Opposite axis or negative angle • Unit quaternion space is – closed under multiplication and inverse, – but not closed under addition and subtraction

Unit Quaternion Algebra • Antipodal equivalence – q and –q represent the same rotation – ex) rotation by p-q about opposite direction – 2 -to-1 mapping between S 3 and SO(3) – Twice as fast as in SO(3)

3 D Orientations and Rotations Orientations and rotations are different in coordinate-invariant geometric programming Use unit quaternions for orientation representation – 3 x 3 orthogonal matrix is theoretically identical Use 3 -vectors for rotation representation

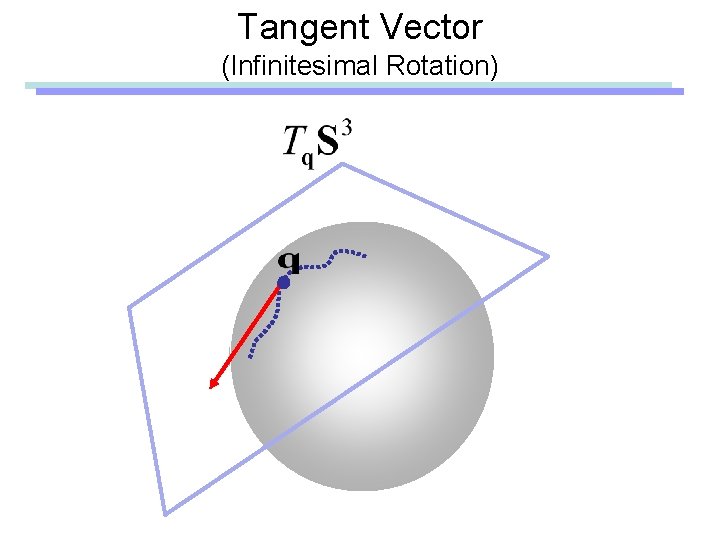
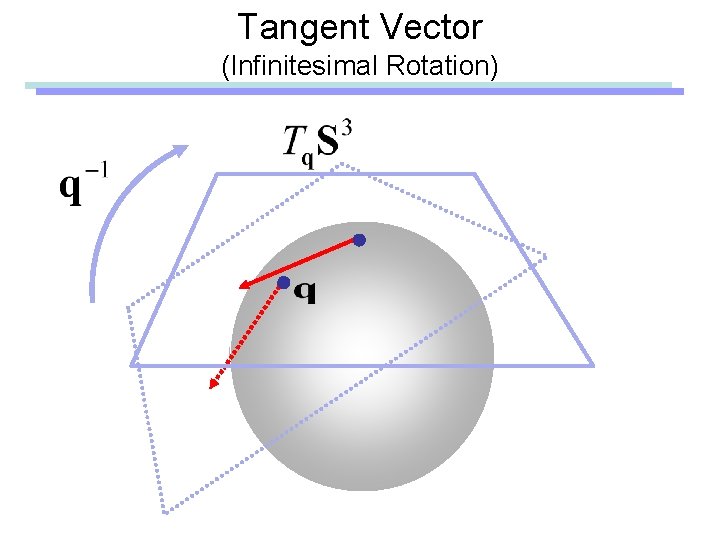
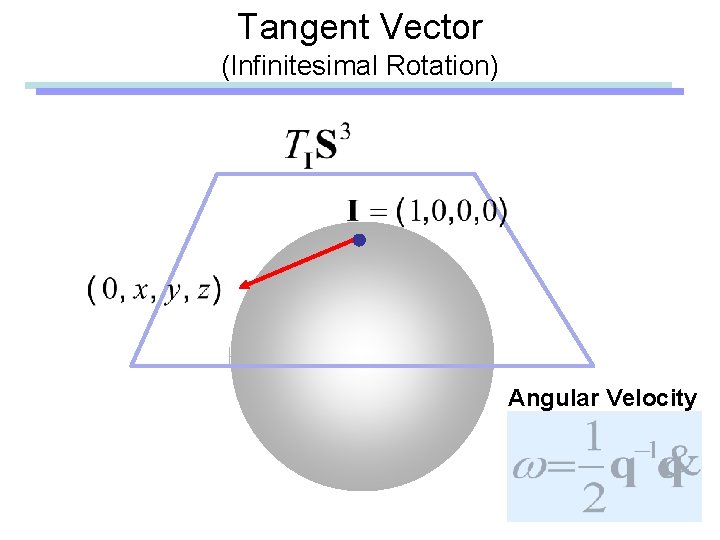
Tangent Vector (Infinitesimal Rotation)

Tangent Vector (Infinitesimal Rotation)

Tangent Vector (Infinitesimal Rotation) Angular Velocity

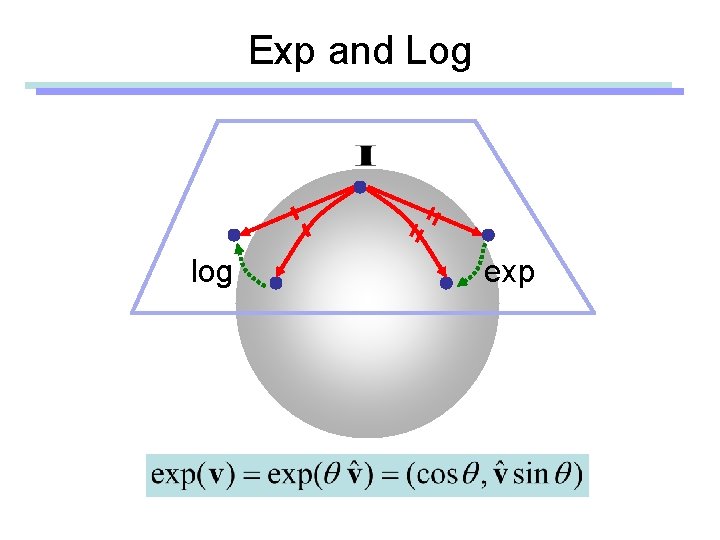
Exp and Log log exp

Exp and Log log exp Euler parameters

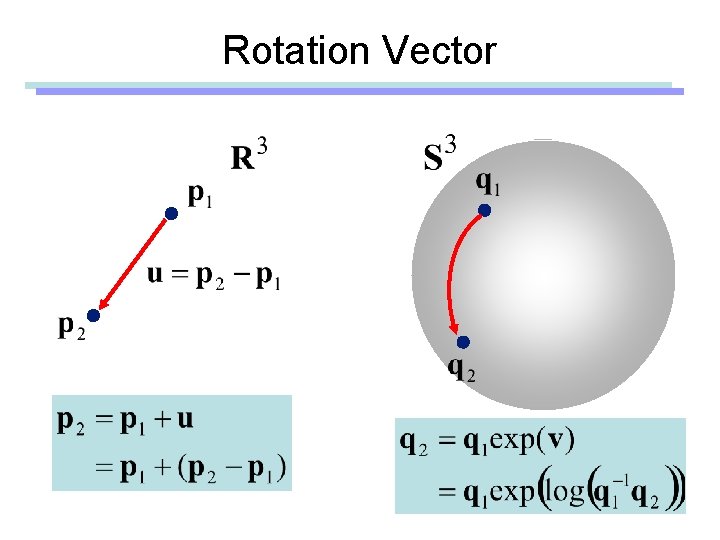
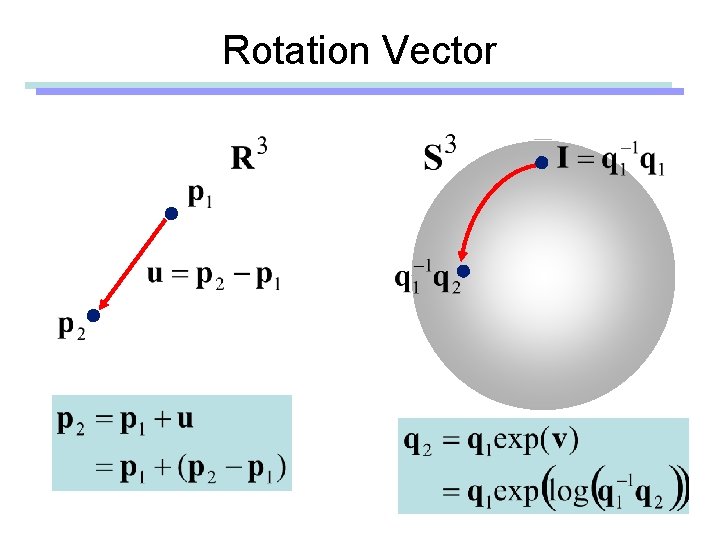
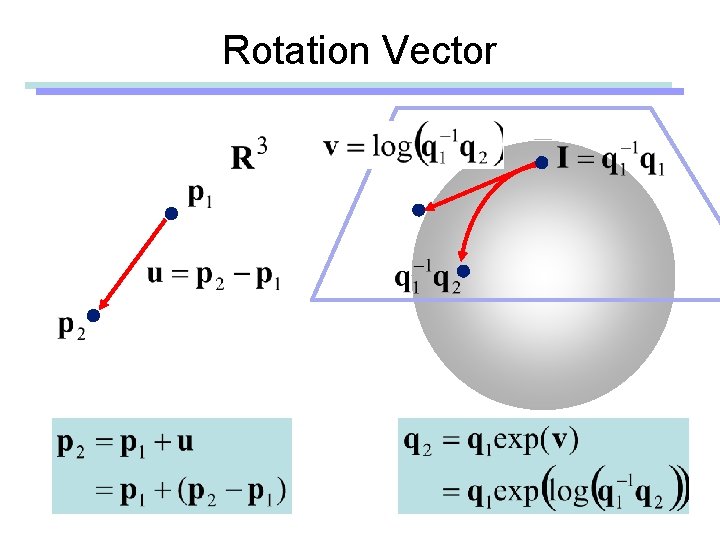
Rotation Vector

Rotation Vector

Rotation Vector

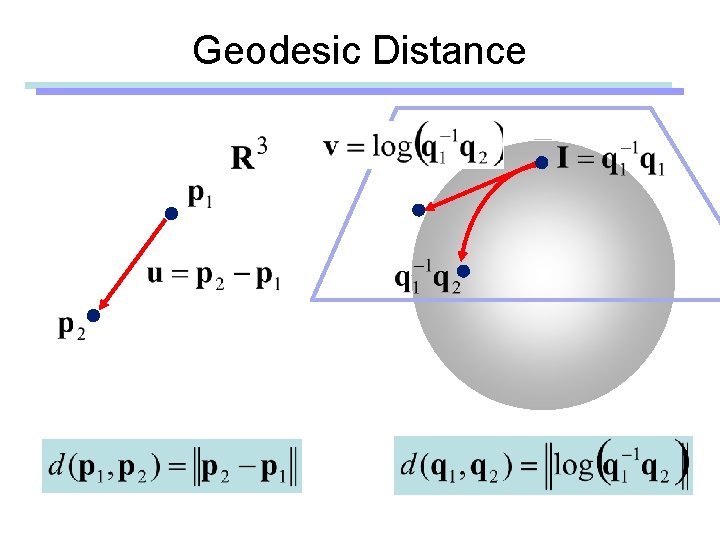
Geodesic Distance

Coordinate-Invariant Operations

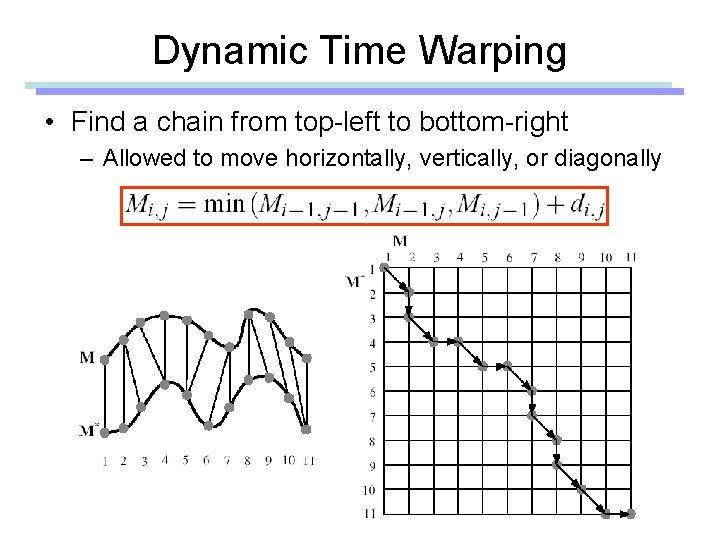
Dynamic Time Warping • The vertex correspondence problem – Minimize the sum of distances between corresponding vertices – The correspondence must be continuous • No missing vertices • No cross edges (No turning back in time) Signal A Signal B

Dynamic Time Warping • Find a chain from top-left to bottom-right – Allowed to move horizontally, vertically, or diagonally