Comparing Means from Two Data Sets The ttest

Comparing Means from Two Data Sets The t-test 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 1

Research Questions • To improve muscular power, should an athlete perform heavy resistance exercises, or light plyometric exercises? • Is it better to imagine the flight of the ball or the actions of your swing prior to striking a golf ball? • Is running 5 km or walking 5 km better for burning calories? • Do golfers sink more putts if they focus on the hole or on the ball during a putt? • Will squatting to a lower depth during a vertical jump improve performance? 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 2

The t-test • All of the questions posed on the previous slide can be statistically addressed using the t-test. • A t-test determines if two groups of data are significantly different (not meaningfully different). • A t-test is the ratio of the actual difference between two means to the difference that is expected due to chance alone. • The bigger the actual difference is compared to the expected difference due to chance, the more statistically significant the t-test. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 3

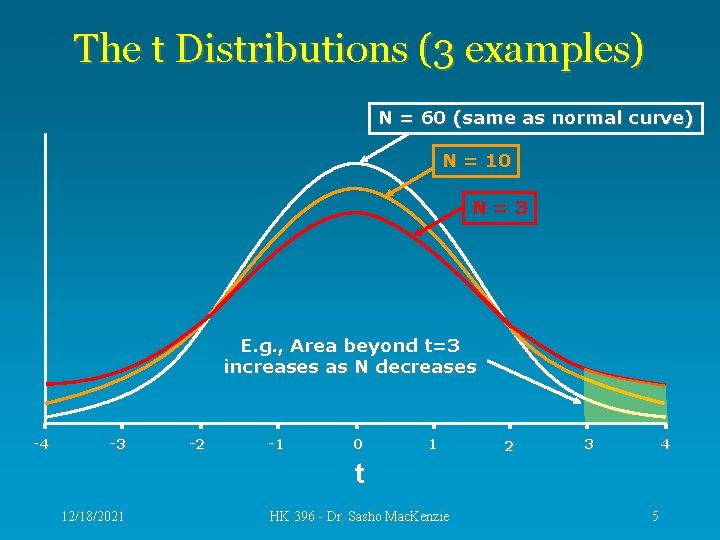
The t-test • A t-test calculation produces a value (t-statistic) that is similar to a z-score. • The t-distributions, are also very similar to the z -score distribution (normal distribution). • The t-distribution changes depending on the sample size. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 4

The t Distributions (3 examples) N = 60 (same as normal curve) N = 10 N=3 E. g. , Area beyond t=3 increases as N decreases -4 -3 -2 -1 0 1 2 4 3 t 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 5

Let’s use an Example • Question: Do HK students drink more or less alcohol than the average St. FX student? • Assumptions: – Every student on campus honestly completed a form and the average drinks/week is known. – Therefore, we know the mean of the population. • Methods: – Determine the drinks/week for a sample of HK students. – Determine if the sample mean is “different” than the population mean (perform a t-test). 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 6

What is “different”? • Before the t-test, we must set a standard for statistical significance. • This means determining the chance of error we are willing to have in our final decision. • I. e. , How confident do we want to be in our decision that HK students drink a different amount? • This decision is represented by alpha ( ), which is typically set at. 05 (5%). This value is arbitrary. • Assume no difference and that the study is repeated 100 times. On 5 occasions, due to chance, we would incorrectly find that HK students drink more. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 7

One-sample t-test • We will use what’s called a one-sample t-test. • This compares the mean of a sample to the mean of a population. Actual difference Expected difference due to chance • X • • SEM 12/18/2021 = sample mean = population mean = standard error of the mean HK 396 - Dr. Sasho Mac. Kenzie 8

The Hypothesis • In statistics you must clearly state a testable hypothesis. • Typically the hypothesis tested is opposite to what you expect and is referred to as the null hypothesis. • Our null hypothesis is that HK students do not drink a different amount than the average university student. • X = or X - = 0 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 9

The Calculation • University Population – Average drinks per week = 10 • HK Sample of students – Mean = 12, SD = 5, N = 30 • The odds of getting a t stat this big, or bigger, due to chance would then be determined by calculating a p-value. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 10

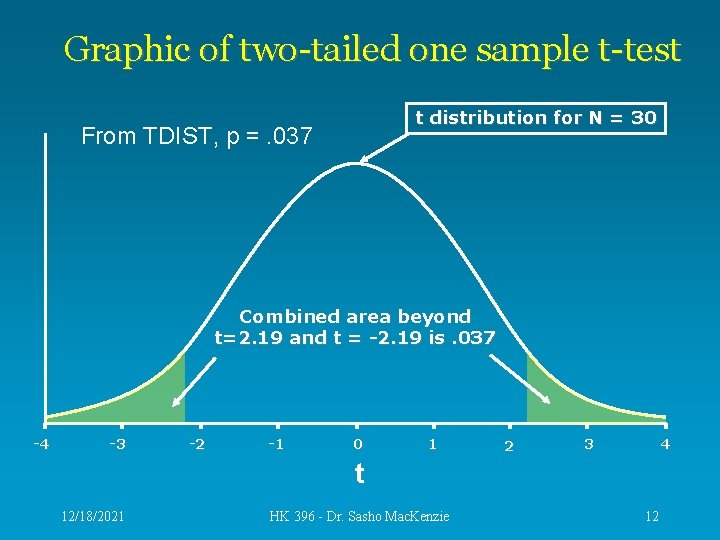
The P-value • In Excel, the function TDIST() can be used to calculate the p-value. • The degrees of freedom are N-1. • Our example is a two-tailed test because HK students may drink more, or less, than the average. I. e. , the sample mean could be either more or less than the population. • Since we set alpha =. 05, if the p-value is less than. 05, we will state HK students are statistically different. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 11

Graphic of two-tailed one sample t-test t distribution for N = 30 From TDIST, p =. 037 Combined area beyond t=2. 19 and t = -2. 19 is. 037 -4 -3 -2 -1 0 1 2 4 3 t 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 12

Conclusion • Since p=. 037 is less than alpha =. 05, we reject the null hypothesis and conclude that HK students consume significantly more drinks per week. • The following shows how this would be explained in a study. • It was determined that the average number of alcoholic drinks consumed by HK students (12 drinks), per week, was significantly more than the typical university student (10 drinks), t(29) = 2. 19, p =. 037. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 13

Independent t-test • Determines if two sample means are statistically different. • The null hypothesis is that the means come from the same population, X 1 - X 2 = 0. • The bottom part of the t-stat now reflects the SEM for both samples, but is still a measure of how much you could expect the means of two samples from the same population to differ due to chance. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 14

The Equation • The stuff on the bottom of the equation is called the standard error of the difference. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 15

Independent t-test example • Do HK students drink more or less than Chemistry students? • Null Hypothesis: HK students and Chemistry students drink the same amount of alcohol per week. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 16

The Calculation • HK sample of students – Mean = 12, SD = 5, N = 30 • Chemistry sample of students – Mean = 10, SD = 3, N = 30 • The odds of getting a t stat this big, or bigger, due to chance would then be determined by calculating a p-value. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 17

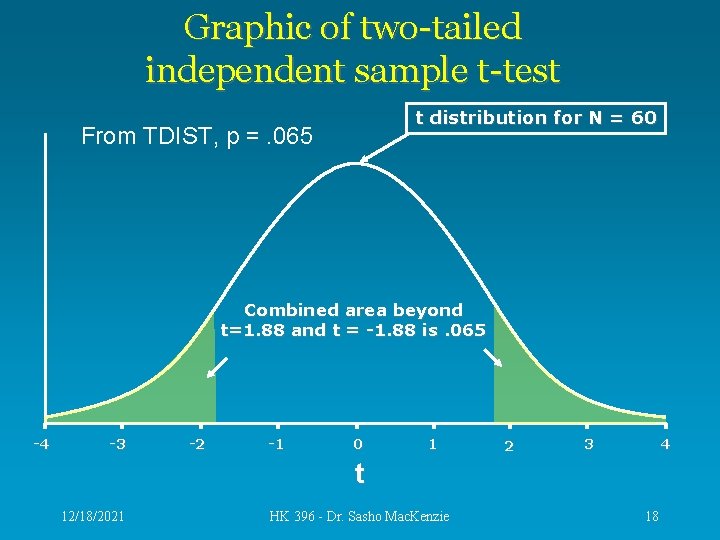
Graphic of two-tailed independent sample t-test t distribution for N = 60 From TDIST, p =. 065 Combined area beyond t=1. 88 and t = -1. 88 is. 065 -4 -3 -2 -1 0 1 2 4 3 t 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 18

Conclusion • Since p=. 065 is greater than alpha =. 05, we cannot reject the null hypothesis. There is not enough evidence to suggest HK students drink more or less than Chemistry students • In a study it would be written as: • It was determined that the average number of alcoholic drinks consumed by HK students (12 drinks), per week, was not significantly different than the Chemistry students (10 drinks), t(58) = 1. 88, p =. 065. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 19

Dependent (Paired) t-test • Determines if two correlated sample means are statistically different. • Required when the same subjects are measured twice. E. g. , Pre-test, Post-test study. • Adjustments are made in how the variability (SD) in the sample data is calculated. This reduces the denominator in the t-statistic and therefore increases the t-statistic. • This accounts for reduction in the t-statistic due to the fact that the same subjects measured twice will show a smaller mean difference than two completely separate groups. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 20

The Difference • Before any group means or standard deviations are calculated, the difference scores between the two measurement times is determined. • For example, if you have a column of pre-test scores and a column of post-test scores, then generate a third column of post minus pre scores. • The t-statistic is then calculated using information from the column of difference scores. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 21

The Equation • The variables in this equations come from a single column of difference scores. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 22

Dependent t-test example • Do HK students drink more alcohol on the Saturday prior to a Biomechanics midterm, or on the following Saturday? • Null Hypothesis: HK students drink the same amount or less on the following Saturday, compared to the Saturday preceding a Biomechanics midterm. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 23

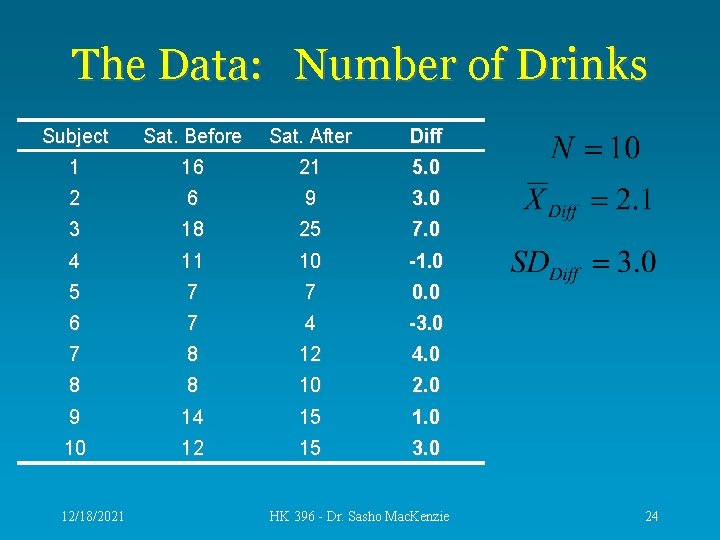
The Data: Number of Drinks Subject Sat. Before Sat. After Diff 1 16 21 5. 0 2 6 9 3. 0 3 18 25 7. 0 4 11 10 -1. 0 5 7 7 0. 0 6 7 4 -3. 0 7 8 12 4. 0 8 8 10 2. 0 9 14 15 1. 0 10 12 15 3. 0 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 24

The Calculation • Difference Scores (Before – After) – Mean = 2. 1, SD = 3. 0, N = 10 • The odds of getting a t stat this big, or bigger, due to chance would then be determined by calculating a p-value. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 25

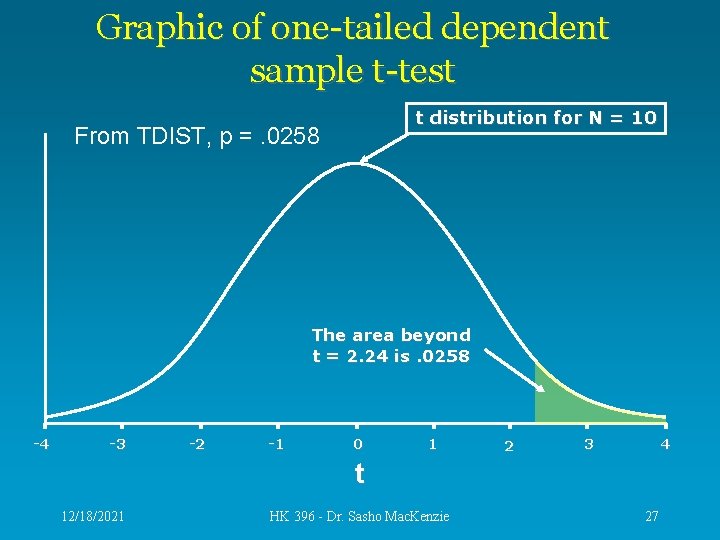
The P-value • In Excel, the function TDIST() can be used to calculate the p-value. • The degrees of freedom are (Npairs - 1). • Our example is a one-tailed test because we are assuming HK students drink more following a midterm. This may not be a good assumption, but I needed a one-tailed example. • Set alpha =. 05, if the p-value is less than. 05, we will state HK students drink significantly more following a biomechanics midterm. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 26

Graphic of one-tailed dependent sample t-test t distribution for N = 10 From TDIST, p =. 0258 The area beyond t = 2. 24 is. 0258 -4 -3 -2 -1 0 1 2 4 3 t 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 27

Conclusion • Since p=. 0258 is less than alpha =. 05, we reject the null hypothesis and conclude that HK students consume significantly more drinks on the Saturday following a midterm. • The following shows how this would be explained in a study. • It was determined that HK students consume significantly more alcoholic drinks (2. 1 more) on a Saturday after a midterm than on a Saturday before a midterm, t(9) = 2. 24, p =. 0258. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 28

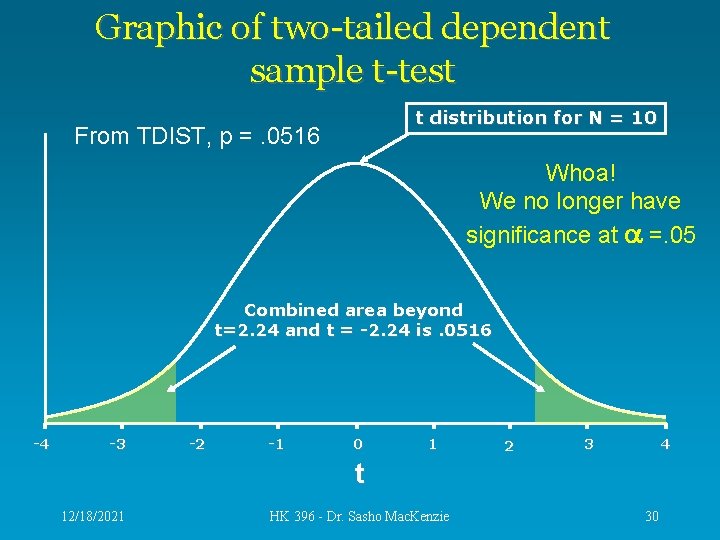
What if the t-test was two-tailed? • The null hypothesis would not be: HK students drink the same amount or less on the following Saturday, compared to the Saturday preceding a Biomechanics midterm. • But rather it would be: HK students drink the same amount on the following Saturday, compared to the Saturday preceding a Biomechanics midterm. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 29

Graphic of two-tailed dependent sample t-test t distribution for N = 10 From TDIST, p =. 0516 Whoa! We no longer have significance at =. 05 Combined area beyond t=2. 24 and t = -2. 24 is. 0516 -4 -3 -2 -1 0 1 2 4 3 t 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 30

Interpreting the P-value • In an experiment of this size, if the populations really have the same mean, what is the probability of observing at least as large a difference between sample means as was, in fact, observed? • There is a p% chance of observing a difference as large as you observed even if the two population means are identical (the null hypothesis is true). • Random sampling from identical populations would lead to a difference smaller than you observed in 1 -p% of experiments, and larger than you observed in p% of experiments. 12/18/2021 HK 396 - Dr. Sasho Mac. Kenzie 31