Comparing Functions Represented in Different ways Graphs vs

Comparing Functions Represented in Different ways Graphs vs. Equations vs. Tables vs. Verbal Descriptions 1. Look at the problem 2. Complete the following for each problem: • Determine if the functions are linear or nonlinear • Compare the slopes of the functions • Compare the y-intercepts of the functions 3. Click to see the answers 4. Follow prompts to see explanations

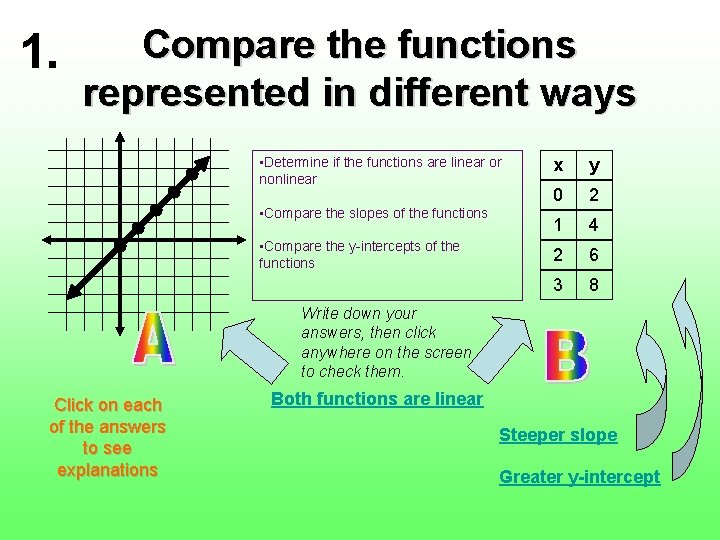
1. Compare the functions represented in different ways • Determine if the functions are linear or nonlinear • Compare the slopes of the functions • Compare the y-intercepts of the functions x y 0 2 1 4 2 6 3 8 Write down your answers, then click anywhere on the screen to check them. Click on each of the answers to see explanations Both functions are linear Steeper slope Greater y-intercept

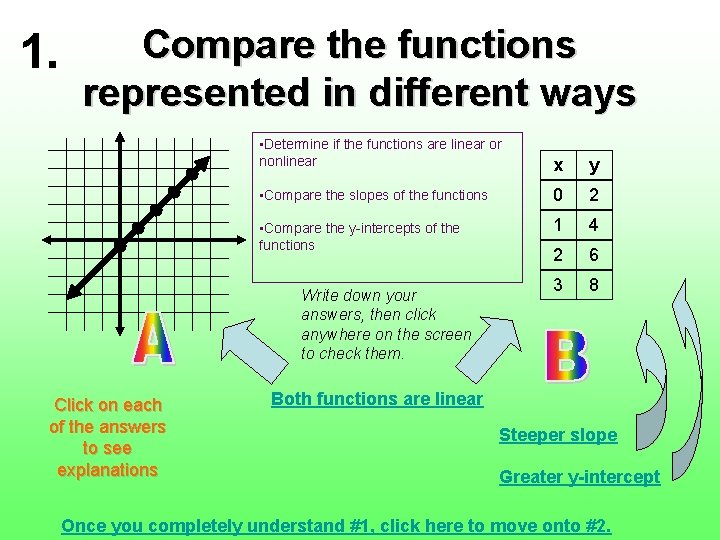
1. Compare the functions represented in different ways • Determine if the functions are linear or nonlinear x y • Compare the slopes of the functions 0 2 • Compare the y-intercepts of the functions 1 4 2 6 3 8 Write down your answers, then click anywhere on the screen to check them. Click on each of the answers to see explanations Both functions are linear Steeper slope Greater y-intercept Once you completely understand #1, click here to move onto #2.

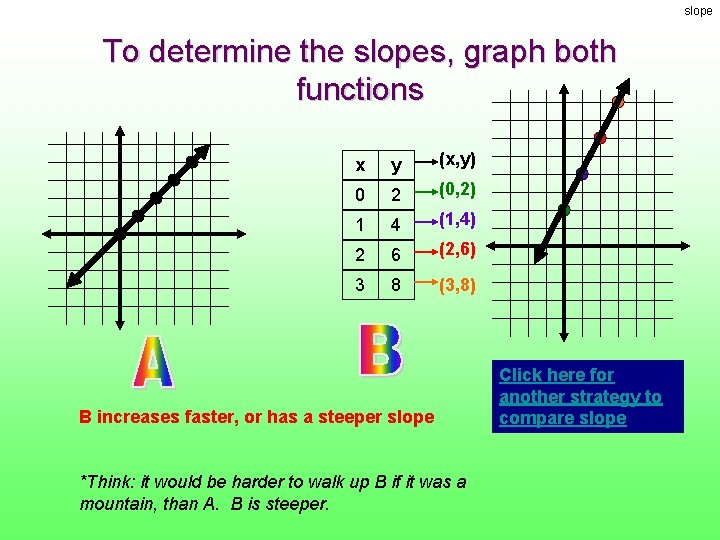
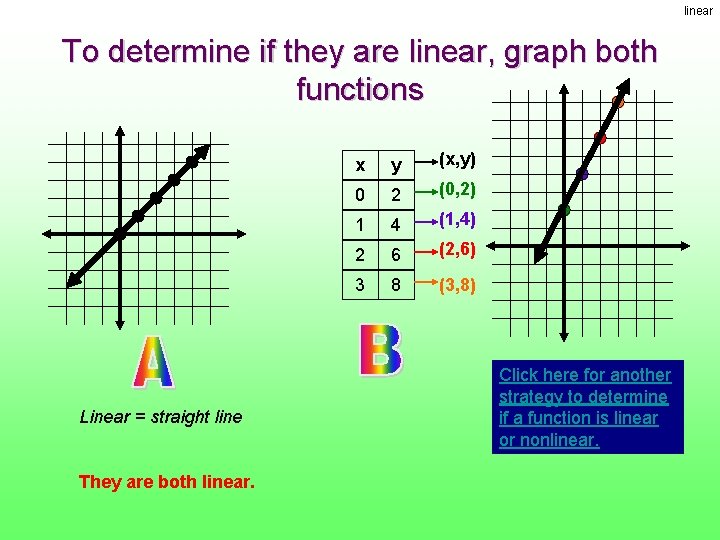
slope To determine the slopes, graph both functions x y (x, y) 0 2 (0, 2) 1 4 (1, 4) 2 6 (2, 6) 3 8 (3, 8) B increases faster, or has a steeper slope *Think: it would be harder to walk up B if it was a mountain, than A. B is steeper. Click here for another strategy to compare slope

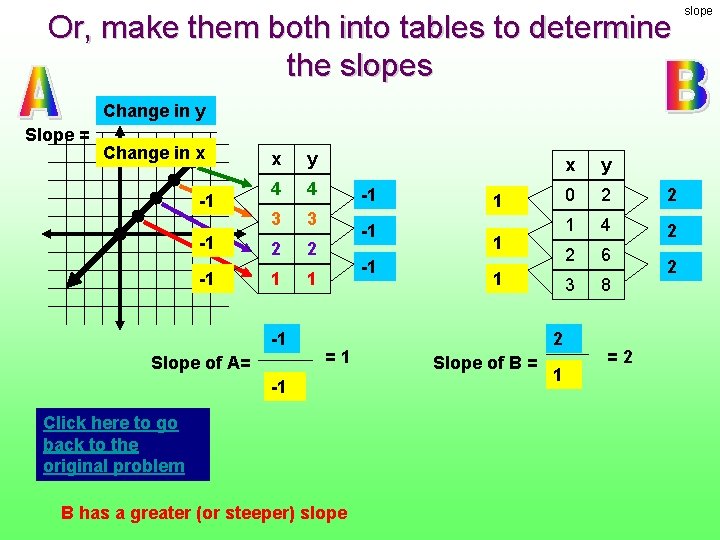
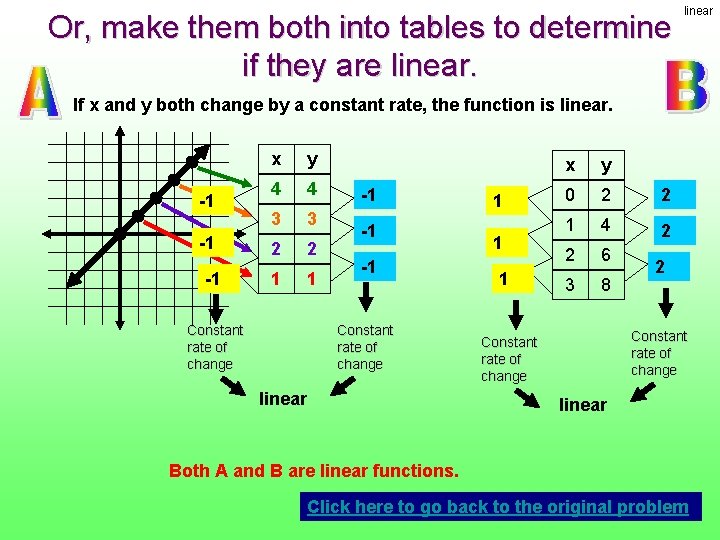
Or, make them both into tables to determine the slopes Change in y Slope = Change in x -1 -1 -1 x y 4 4 3 3 2 2 1 1 -1 Slope of A= -1 -1 -1 =1 -1 Click here to go back to the original problem B has a greater (or steeper) slope 1 1 1 2 Slope of B = 1 x y 0 2 2 1 4 2 2 6 3 8 =2 2 slope

linear To determine if they are linear, graph both functions Linear = straight line They are both linear. x y (x, y) 0 2 (0, 2) 1 4 (1, 4) 2 6 (2, 6) 3 8 (3, 8) Click here for another strategy to determine if a function is linear or nonlinear.

Or, make them both into tables to determine if they are linear If x and y both change by a constant rate, the function is linear. -1 -1 -1 x y 4 4 3 3 2 2 1 1 Constant rate of change -1 -1 -1 Constant rate of change linear 1 1 1 x y 0 2 2 1 4 2 2 6 3 8 2 Constant rate of change linear Both A and B are linear functions. Click here to go back to the original problem

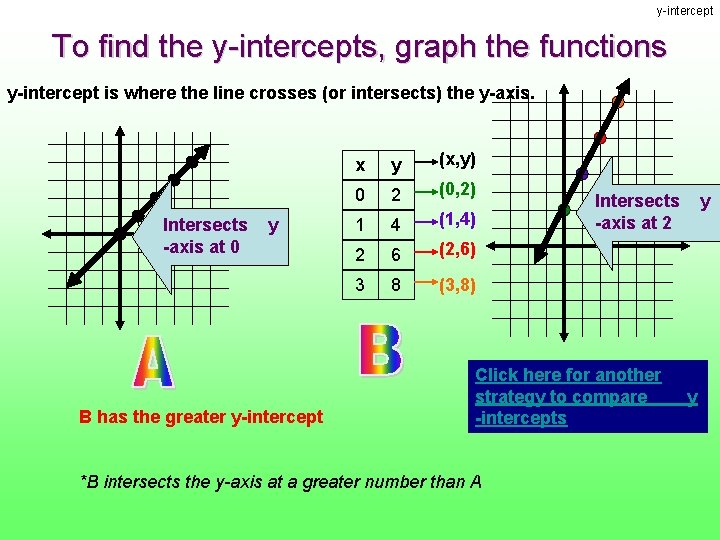
y-intercept To find the y-intercepts, graph the functions y-intercept is where the line crosses (or intersects) the y-axis. Intersects -axis at 0 y B has the greater y-intercept x y (x, y) 0 2 (0, 2) 1 4 (1, 4) 2 6 (2, 6) 3 8 (3, 8) Intersects -axis at 2 Click here for another strategy to compare -intercepts *B intersects the y-axis at a greater number than A y y

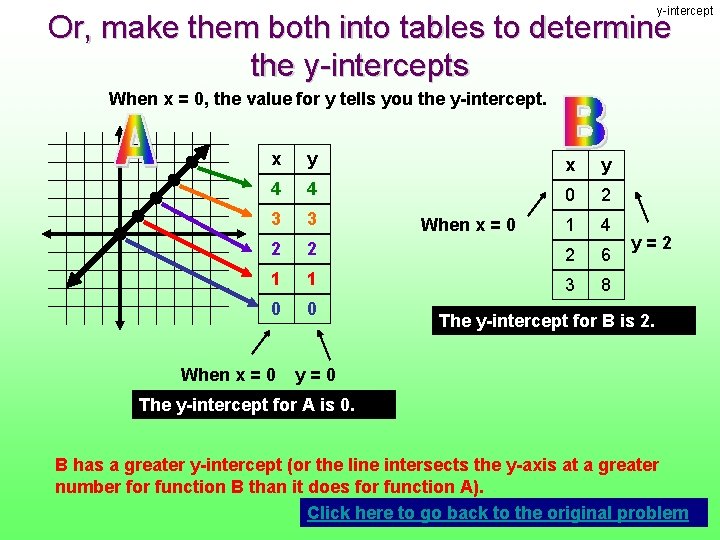
y-intercept Or, make them both into tables to determine the y-intercepts When x = 0, the value for y tells you the y-intercept. x y 4 4 0 2 3 3 1 4 2 2 2 6 1 1 3 8 0 0 When x = 0 y=2 The y-intercept for B is 2. y=0 The y-intercept for A is 0. B has a greater y-intercept (or the line intersects the y-axis at a greater number for function B than it does for function A). Click here to go back to the original problem

2. Compare the functions represented in different ways y = 3 x +4 • Determine if the functions are linear or nonlinear • Compare the slopes of the functions • Compare the y-intercepts of the functions Write down your answers, then click anywhere on the screen to check them. C has a greater y-intercept than D Click on each answer to see the explanations x y 0 0 2 3 4 4 6 5 8 6 C is linear; D is nonlinear C has a slope of 3; D does not have a slope because it is nonlinear

2. Compare the functions represented in different ways y = 3 x +4 • Determine if the functions are linear or nonlinear • Compare the slopes of the functions • Compare the y-intercepts of the functions Write down your answers, then click anywhere on the screen to check them. C has a greater y-intercept than D Click on each answer to see the explanations x y 0 0 2 3 4 4 6 5 8 6 C is linear; D is nonlinear C has a slope of 3; D does not have a slope because it is nonlinear Once you completely understand #2, click here to move onto #3.

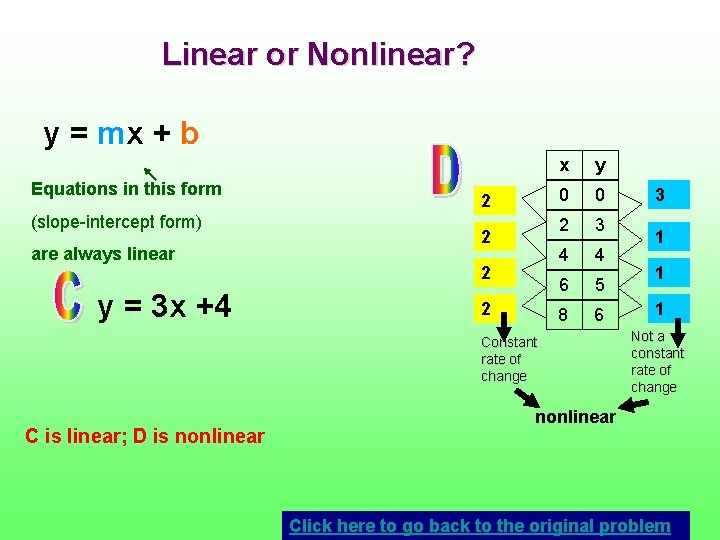
Linear or Nonlinear? y = mx + b Equations in this form (slope-intercept form) are always linear y = 3 x +4 2 2 x y 0 0 2 3 4 4 6 5 8 6 Constant rate of change C is linear; D is nonlinear 3 1 1 1 Not a constant rate of change nonlinear Click here to go back to the original problem

Compare the slopes y = mx + b m = slope 2 2 2 y = 3 x +4 2 x y 0 0 2 3 4 4 6 5 8 6 Constant rate of change slope = 3 3 1 1 1 Not a constant rate of change nonlinear C has a slope of 3; D does not have a slope because it is nonlinear No slope Click here to go back to the original problem

Compare the y-intercepts y-intercept = the y value when x = 0 y = mx + b b = y-intercept when x = 0 y = 3 x +4 y-intercept = 4 x y 0 0 2 3 4 4 6 5 8 6 y-intercept = 0 C has a greater y-intercept than D Click here to go back to the original problem y=0

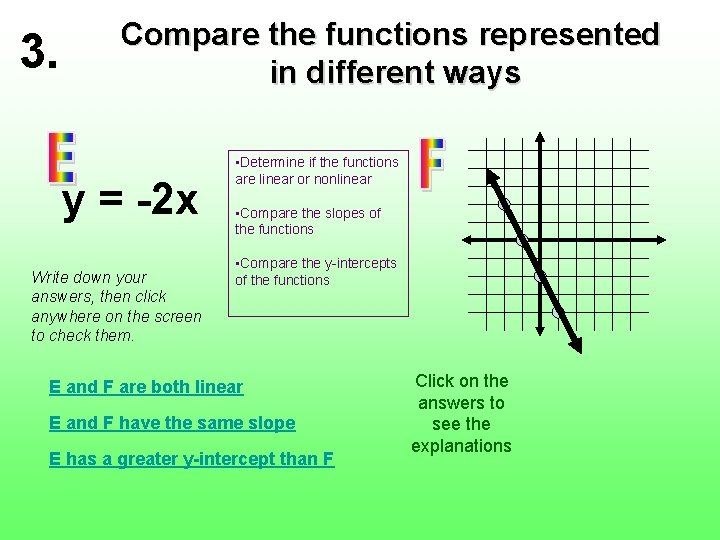
3. Compare the functions represented in different ways y = -2 x Write down your answers, then click anywhere on the screen to check them. • Determine if the functions are linear or nonlinear • Compare the slopes of the functions • Compare the y-intercepts of the functions E and F are both linear E and F have the same slope E has a greater y-intercept than F Click on the answers to see the explanations

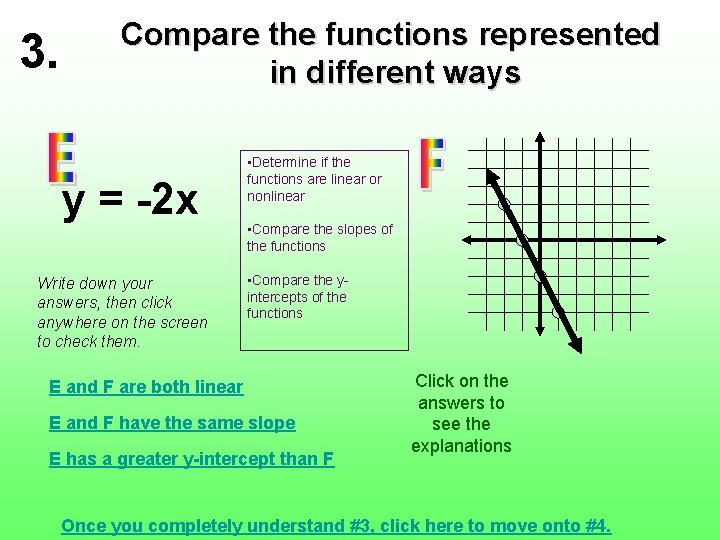
3. Compare the functions represented in different ways y = -2 x Write down your answers, then click anywhere on the screen to check them. • Determine if the functions are linear or nonlinear • Compare the slopes of the functions • Compare the yintercepts of the functions E and F are both linear E and F have the same slope E has a greater y-intercept than F Click on the answers to see the explanations Once you completely understand #3, click here to move onto #4.

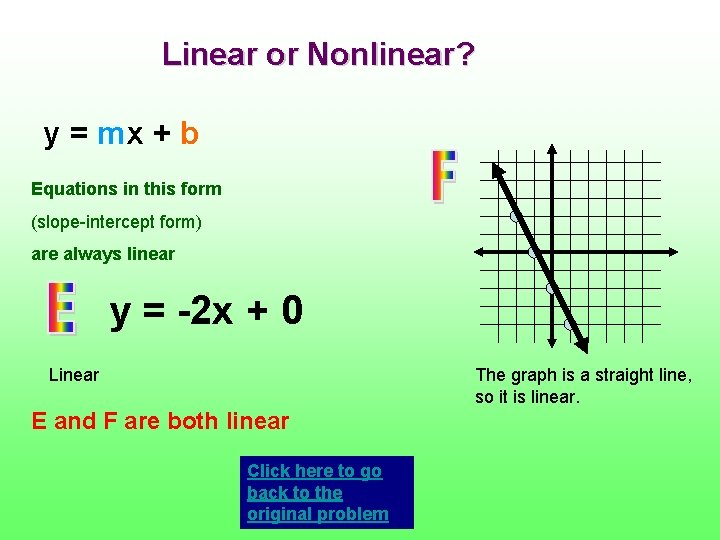
Linear or Nonlinear? y = mx + b Equations in this form (slope-intercept form) are always linear y = -2 x + 0 Linear The graph is a straight line, so it is linear. E and F are both linear Click here to go back to the original problem

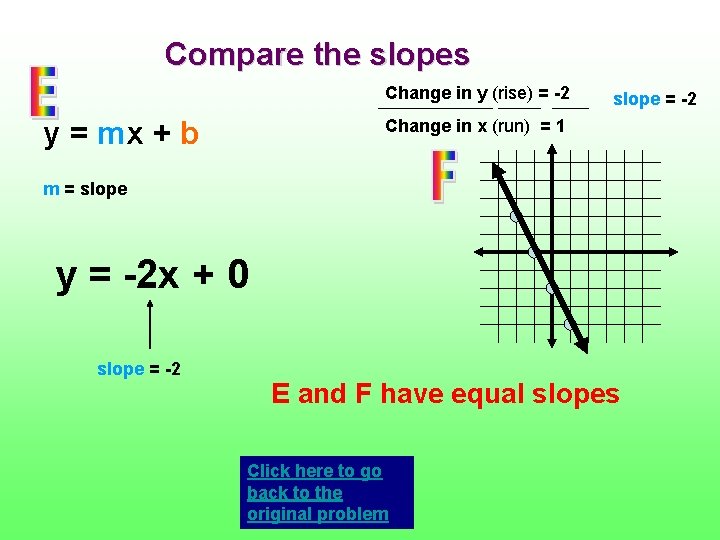
Compare the slopes Change in y (rise) = -2 slope = -2 Change in x (run) = 1 y = mx + b m = slope y = -2 x + 0 slope = -2 E and F have equal slopes Click here to go back to the original problem

Compare the y-intercepts y = mx + b b = y-intercept y = -2 x + 0 y-intercept = 0 E has a greater y-intercept than F Click here to go back to the original problem Intersects y-axis at -2 y-intercept = -2

4 Compare the functions represented in different ways Maggie puts $5 in the bank every • Determine if the functions are linear or week. nonlinear • Compare the slopes of the functions Write down your answers, then click anywhere on the screen to check them. • Compare the y-intercepts of the functions G and H are both linear. G and H have the same y-intercept. G has a greater slope. Click on the answers to see the explanations x y 0 0 1 4 2 8 3 12 4 16

4 Compare the functions represented in different ways Maggie puts $5 in the bank every • Determine if the functions are linear or week. nonlinear Write down your answers, then click anywhere on the screen to check them. x y 0 0 1 4 2 8 • Compare the slopes of the functions 3 12 • Compare the y-intercepts of the functions 4 16 G and H are both linear. G and H have the same y-intercept. Click on the answers to see the explanations G has a greater slope. Once you completely understand #4, click here to move on.

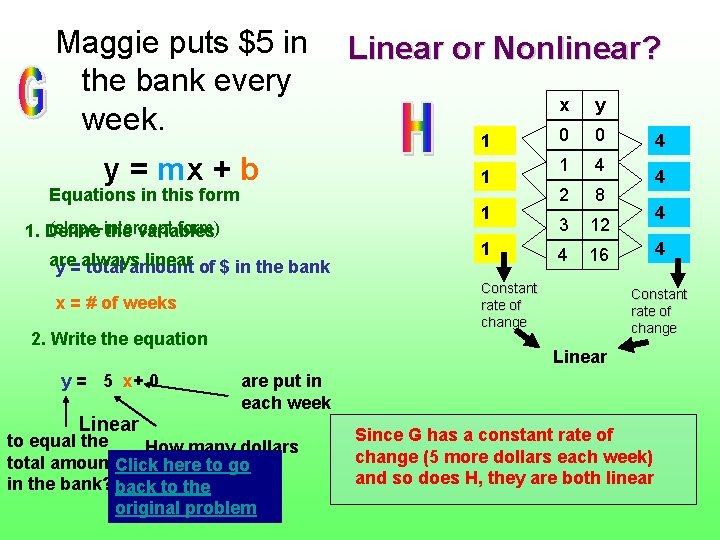
Maggie puts $5 in the bank every week. y = mx + b Equations in this form are linear of $ in the bank y =always total amount 1 1 x y 0 0 1 4 2 8 3 12 4 16 Constant rate of change x = # of weeks 2. Write the equation Linear 1 1 (slope-intercept form) 1. Define the variables y = 5 x+ 0 Linear or Nonlinear? 4 4 Constant rate of change Linear are put in each week to equal the How many dollars total amount. Click here to go in the bank? back to the original problem Since G has a constant rate of change (5 more dollars each week) and so does H, they are both linear

Maggie puts $5 in the bank every week. Compare the slopes 1 y = mx + b 1 m = slope 1. Define the variables 1 1 y = total amount of $ in the bank x y 0 0 1 4 2 8 3 12 4 16 4 4 x = # of weeks 2. Write the equation y = 5 x+ 0 Slope = Change in y Change in x are put in each week. G has a greater slope than H to equal the How many dollars Click here to go total amount slope = 5 back to the in the bank? original problem = 4 1 = 4

Maggie puts $5 in the bank every week. Compare the y-intercepts y = mx + b b = y-intercept 1. Define the variables y = total amount of $ in the bank when x = 0 x y 0 0 1 4 2 8 3 12 4 16 y=0 x = # of weeks 2. Write the equation y = 5 x+ 0 y-intercept = 0 are put in each week to equal the How many dollars total amount y-intercept = 0 Click to go in thehere bank? back to the original problem y – intercepts are equal

Great work! • Now, move on to _____