Comparing Crash Prediction Techniques for Ranking of Sites

Comparing Crash Prediction Techniques for Ranking of Sites in a Network Screening Process Presented by Lalita Thakali University of Waterloo Co-authors Dr. Liping Fu, Professor Dr. Tao Chen, Assistant Professor 1

Outline § Background • Road safety problems • Role of network screening § Research Objectives § Proposed Methods § A Case study § Findings and Conclusions

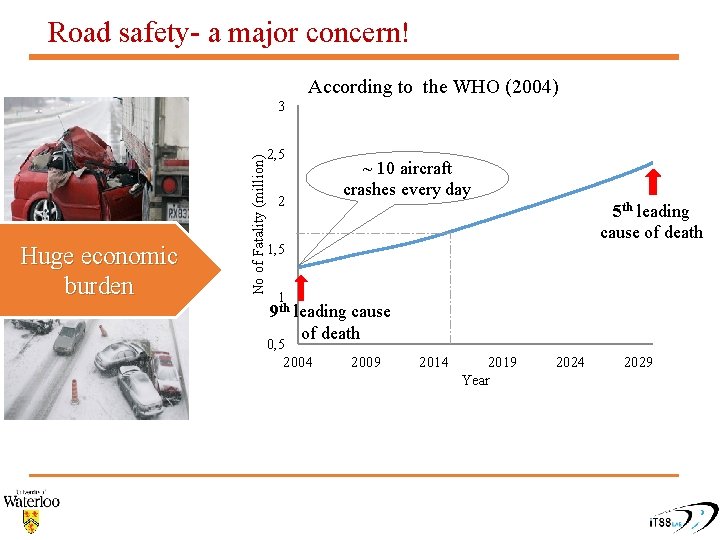
Road safety- a major concern! According to the WHO (2004) Huge economic burden No of Fatality (million) 3 2, 5 2 ~ 10 aircraft crashes every day 5 th leading cause of death 1, 5 1 9 th leading cause of death 0, 5 2004 2009 2014 2019 Year 2024 2029

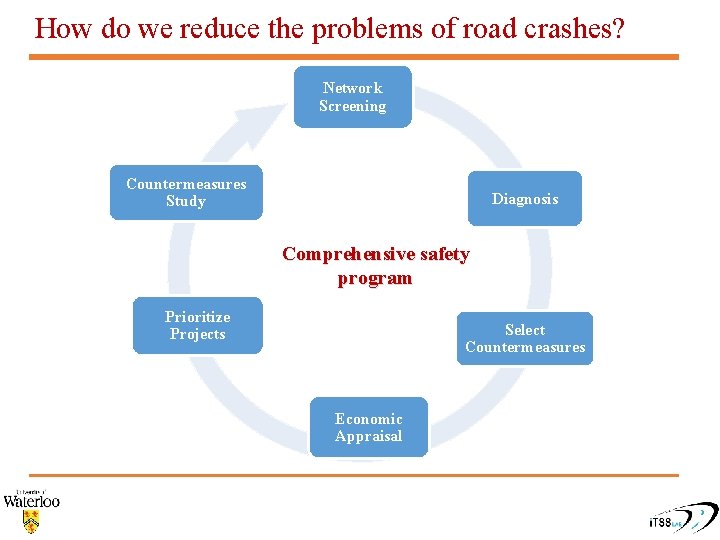
How do we reduce the problems of road crashes? Network Screening Countermeasures Study Diagnosis Comprehensive safety program Prioritize Projects Select Countermeasures Economic Appraisal

Why network screening? Waterloo Limited safety improvement budget! Kitchener Hotspot locations Waterloo Kitchener

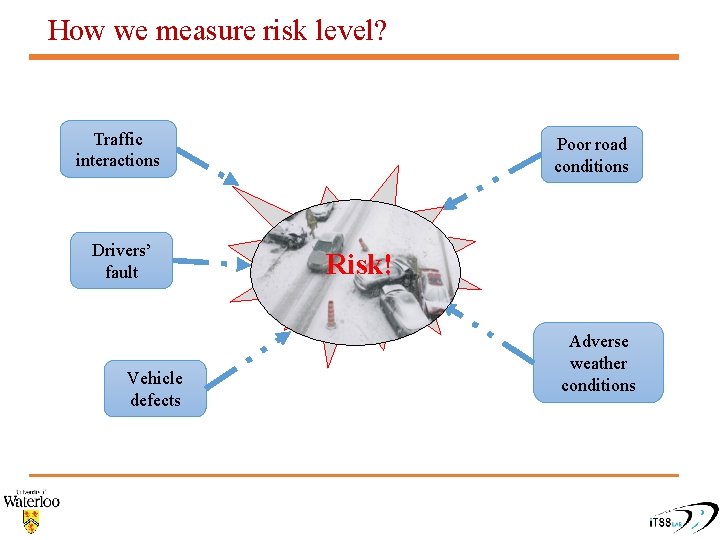
Selecting hotspots in Network Screening needs a risk measuring tool

How we measure risk level? Traffic interactions Drivers’ fault Vehicle defects Poor road conditions Risk! Adverse weather conditions

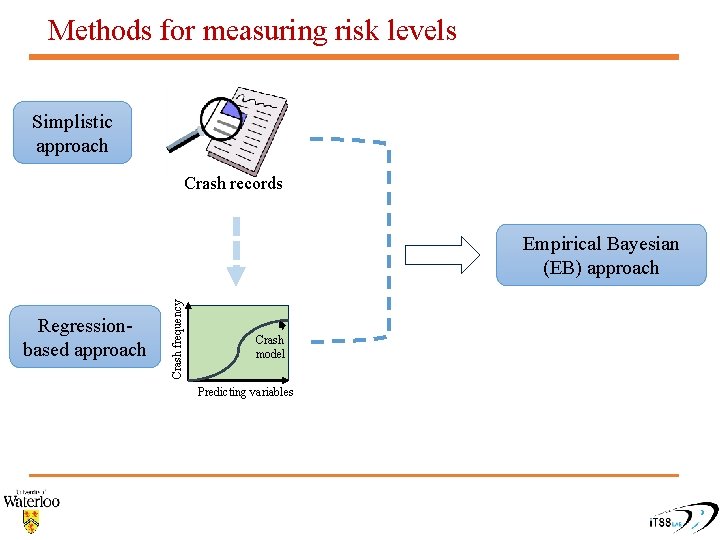
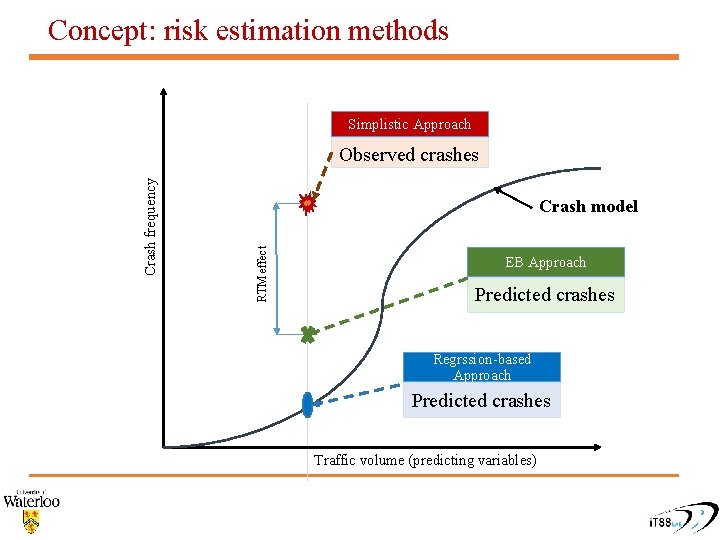
Methods for measuring risk levels Simplistic approach Crash records Regressionbased approach Crash frequency Empirical Bayesian (EB) approach Crash model Predicting variables

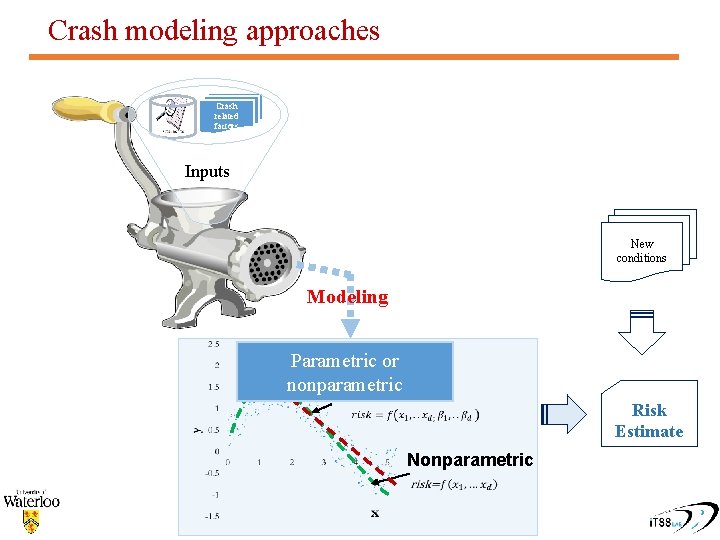
Crash modeling approaches Crash related factors Inputs New conditions Modeling Parametric or nonparametric Parametric Nonparametric Risk Estimate

Research objectives • To propose alternative, nonparametric techniques for modeling crashes. • To compare the performance of nonparametric and parametric models in network screening

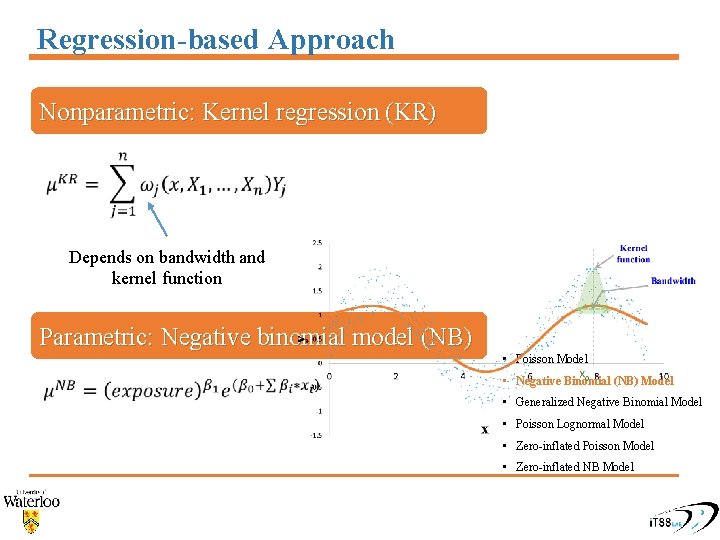
Regression-based Approach Nonparametric: Kernel regression (KR) Depends on bandwidth and kernel function Parametric: Negative binomial model (NB) • Poisson Model • Negative Binomial (NB) Model • Generalized Negative Binomial Model • Poisson Lognormal Model • Zero-inflated Poisson Model • Zero-inflated NB Model

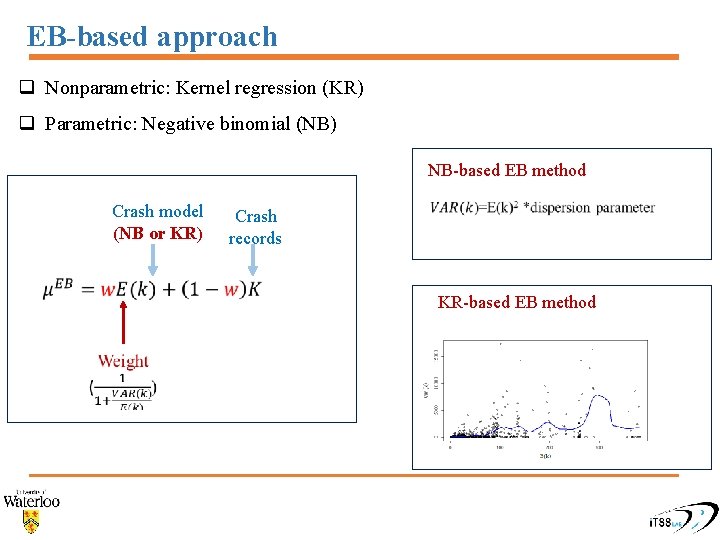
EB-based approach q Nonparametric: Kernel regression (KR) q Parametric: Negative binomial (NB) NB-based EB method Crash model (NB or KR) Crash records KR-based EB method

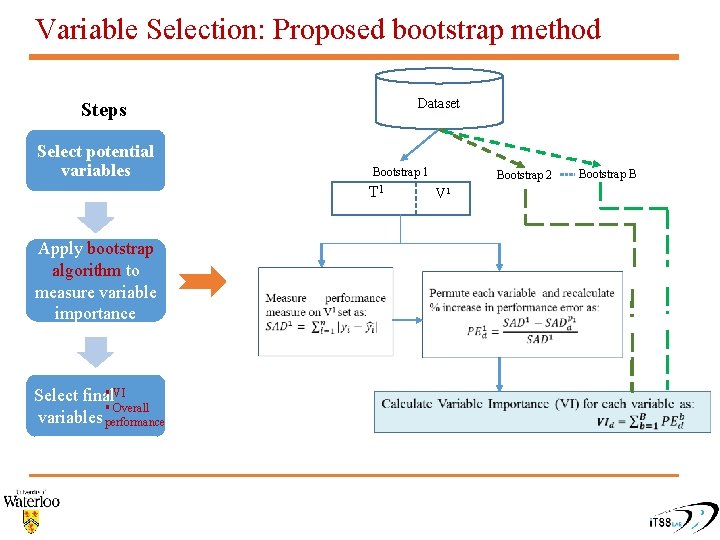
Variable Selection: Proposed bootstrap method Dataset Steps Select potential variables Bootstrap 1 T 1 Apply bootstrap algorithm to measure variable importance § VI Select final § Overall variables performance Bootstrap 2 V 1 Bootstrap B

A Case Study

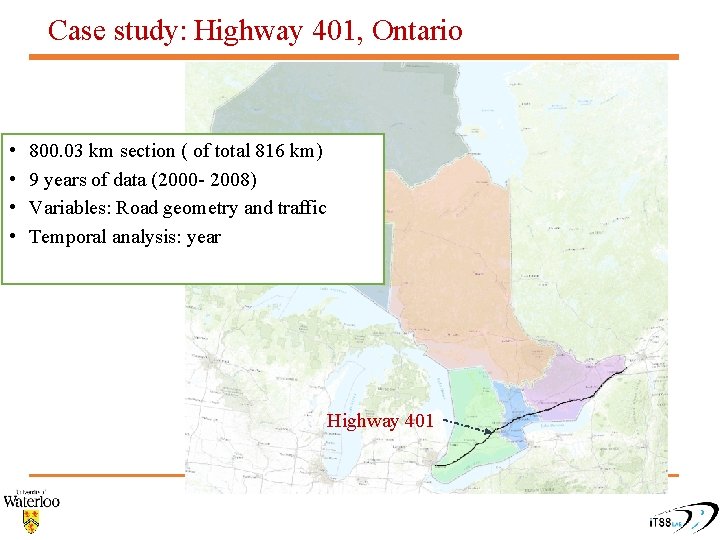
Case study: Highway 401, Ontario • • 800. 03 km section ( of total 816 km) 9 years of data (2000 - 2008) Variables: Road geometry and traffic Temporal analysis: year Highway 401

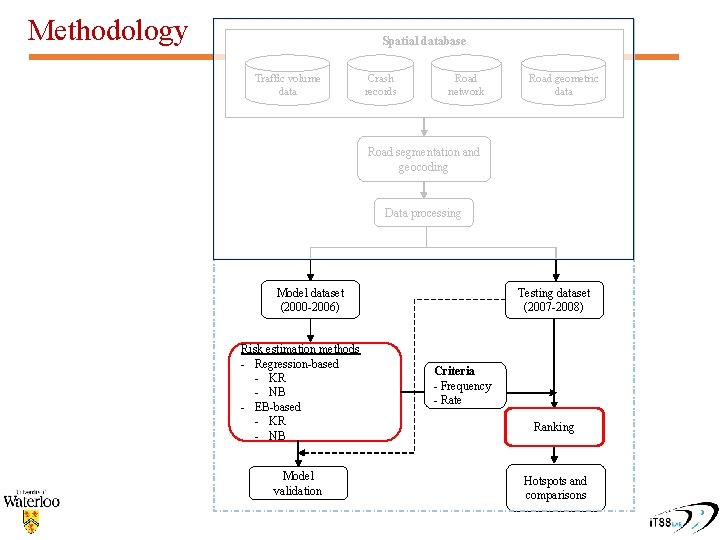
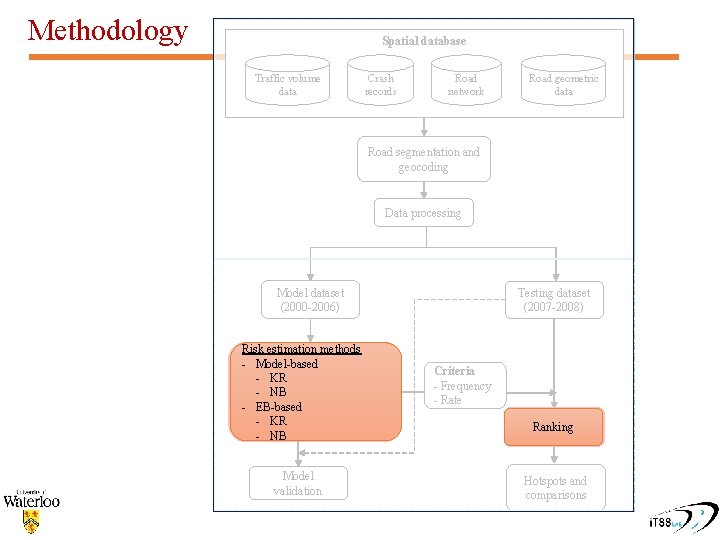
Methodology Spatial database Traffic volume data Crash records Road network Road geometric data Road segmentation and geocoding Data processing Model dataset (2000 -2006) Risk estimation methods - Regression-based - KR - NB - EB-based - KR - NB Model validation Testing dataset (2007 -2008) Criteria - Frequency - Rate Ranking Hotspots and comparisons

Distribution of traffic levels

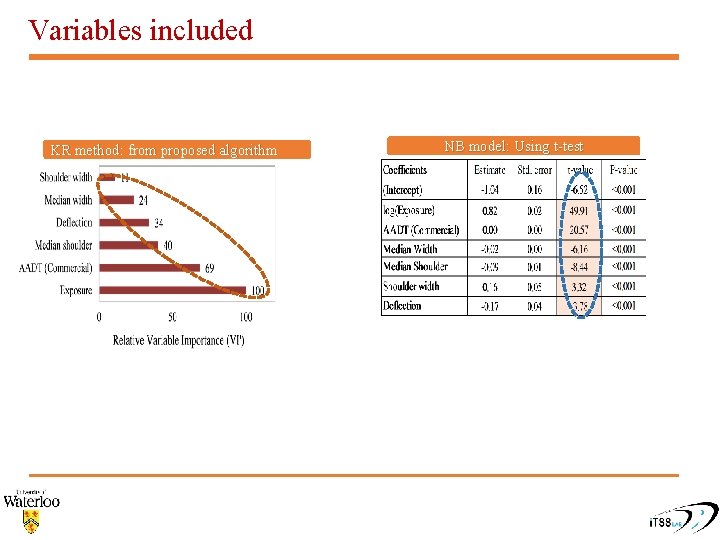
Variables included KR method: from proposed algorithm NB model: Using t-test

Comparison Results (Parametric & Nonparametric)

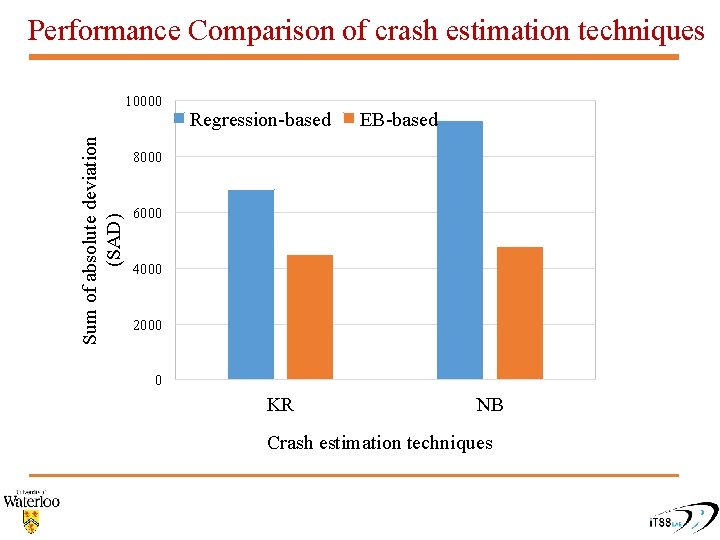
Performance Comparison of crash estimation techniques Sum of absolute deviation (SAD) 10000 Regression-based EB-based 8000 6000 4000 2000 0 KR NB Crash estimation techniques

Methodology Spatial database Traffic volume data Crash records Road network Road geometric data Road segmentation and geocoding Data processing Model dataset (2000 -2006) Risk estimation methods - Model-based - KR - NB - EB-based - KR - NB Model validation Testing dataset (2007 -2008) Criteria - Frequency - Rate Ranking Hotspots and comparisons

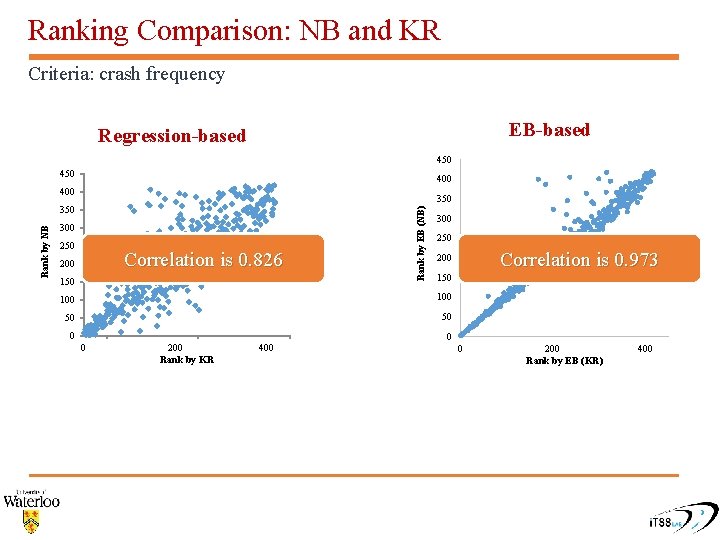
Ranking Comparison: NB and KR Criteria: crash frequency EB-based Regression-based 450 400 Rank by NB 300 250 Correlation is 0. 826 200 150 Rank by EB (NB) 350 300 250 100 100 50 50 0 Correlation is 0. 973 200 0 0 200 Rank by KR 400 0 200 Rank by EB (KR) 400

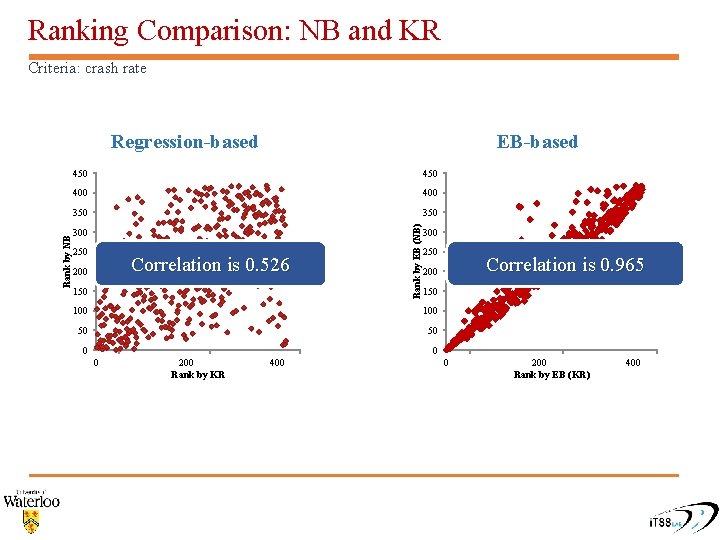
Ranking Comparison: NB and KR Criteria: crash rate EB-based 450 400 350 300 250 Correlation is 0. 526 200 150 Rank by EB (NB) Rank by NB Regression-based 300 250 100 100 50 50 0 Correlation is 0. 965 200 0 0 200 Rank by KR 400 0 200 Rank by EB (KR) 400

Conclusions Ø Introduced an algorithm for selecting variables to KR method. Ø Introduced nonparametric methods (regression-based and EB-based) Ø Performance comparison showed that the nonparametric approach performed better than the parametric. Ø Deviations in crash estimation methods were observed in one to one ranking of sites in network screening. Future works Ø More case studies are recommended to support the study findings

Thank you!

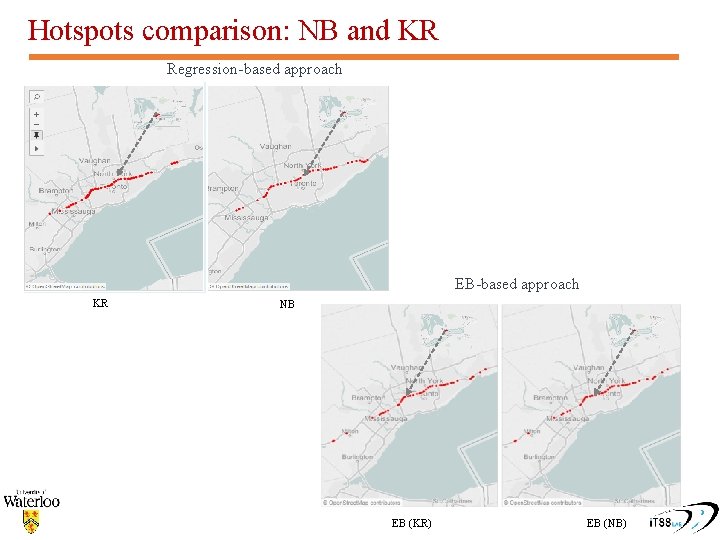
Hotspots comparison: NB and KR Regression-based approach EB-based approach KR NB EB (KR) EB (NB)

Concept: risk estimation methods Simplistic Approach Crash model RTM effect Crash frequency Observed crashes EB Approach Predicted crashes Regrssion-based Approach Predicted crashes Traffic volume (predicting variables)