Comparators Combinational Design Comparators Equality and Magnitude Comparators

Comparators Combinational Design

Comparators • Equality and Magnitude Comparators – CSE 171 (Designed using CUPL) • TTL Comparators • Comparator Networks • Cascading 1 -bit Comparators – Design using VHDL
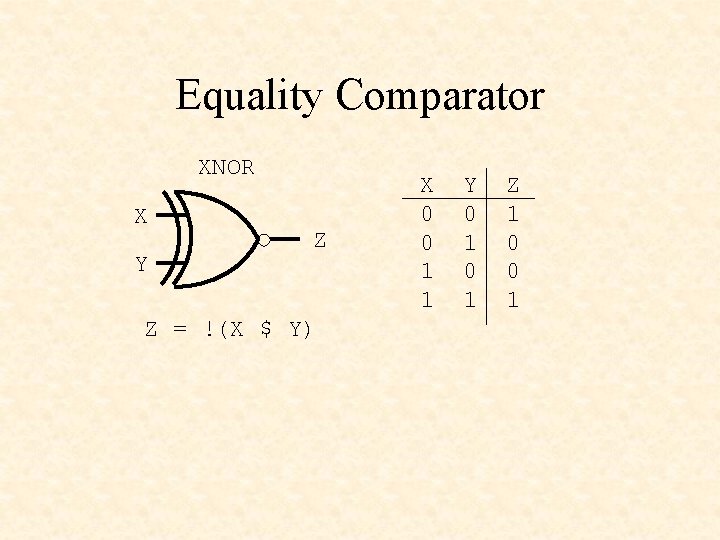
Equality Comparator XNOR X Y Z Z = !(X $ Y) X 0 0 1 1 Y 0 1 Z 1 0 0 1
![4 -Bit Equality Comparator FIELD A = [A 0. . 3]; FIELD B = 4 -Bit Equality Comparator FIELD A = [A 0. . 3]; FIELD B =](http://slidetodoc.com/presentation_image_h2/df27adb1fc628f1c13b87e2c4e0a965d/image-4.jpg)
4 -Bit Equality Comparator FIELD A = [A 0. . 3]; FIELD B = [B 0. . 3]; FIELD C = [C 0. . 3];
![4 -bit Equality Detector A[3. . 0] B[3. . 0] Equality Detector A_EQ_B 4 -bit Equality Detector A[3. . 0] B[3. . 0] Equality Detector A_EQ_B](http://slidetodoc.com/presentation_image_h2/df27adb1fc628f1c13b87e2c4e0a965d/image-5.jpg)
4 -bit Equality Detector A[3. . 0] B[3. . 0] Equality Detector A_EQ_B
![4 -bit Magnitude Comparator A[3. . 0] B[3. . 0] Magnitude Detector A_LT_B A_EQ_B 4 -bit Magnitude Comparator A[3. . 0] B[3. . 0] Magnitude Detector A_LT_B A_EQ_B](http://slidetodoc.com/presentation_image_h2/df27adb1fc628f1c13b87e2c4e0a965d/image-6.jpg)
4 -bit Magnitude Comparator A[3. . 0] B[3. . 0] Magnitude Detector A_LT_B A_EQ_B A_GT_B
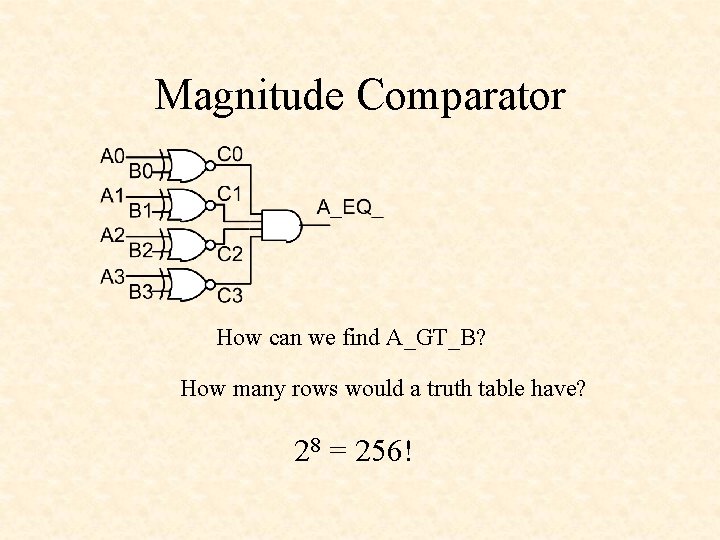
Magnitude Comparator How can we find A_GT_B? How many rows would a truth table have? 28 = 256!

Magnitude Comparator Find A_GT_B If A = 1001 and B = 0111 is A > B? Why? Because A 3 > B 3 i. e. A 3 & !B 3 = 1 Therefore, one term in the logic equation for A_GT_B is A 3 & !B 3

Magnitude Comparator A_GT_B = A 3 & !B 3 # …. . If A = 1101 and B = 1011 is A > B? Why? Because A 3 = B 3 and A 2 > B 2 i. e. C 3 = 1 and A 2 & !B 2 = 1 Therefore, the next term in the logic equation for A_GT_B is C 3 & A 2 & !B 2

Magnitude Comparator A_GT_B = A 3 & !B 3 # C 3 & A 2 & !B 2 # …. . Because A 3 = B 3 and A 2 = B 2 and A 1 > B 1 i. e. C 3 = 1 and C 2 = 1 and A 1 & !B 1 = 1 If A = 1010 and B = 1001 is A > B? Therefore, the next term in the Why? logic equation for A_GT_B is C 3 & C 2 & A 1 & !B 1

Magnitude Comparator A_GT_B = A 3 & !B 3 # C 3 & A 2 & !B 2 # C 3 & C 2 & A 1 & !B 1 # …. . Because A 3 = B 3 and A 2 = B 2 and A 1 = B 1 and If A = 1011 and A 0 > B 0 B = 1010 i. e. C 3 = 1 and C 2 = 1 and is A > B? C 1 = 1 and A 0 & !B 0 = 1 Why? Therefore, the last term in the logic equation for A_GT_B is C 3 & C 2 & C 1 & A 0 & !B 0

Magnitude Comparator A_GT_B = A 3 & !B 3 # C 3 & A 2 & !B 2 # C 3 & C 2 & A 1 & !B 1 # C 3 & C 2 & C 1 & A 0 & !B 0
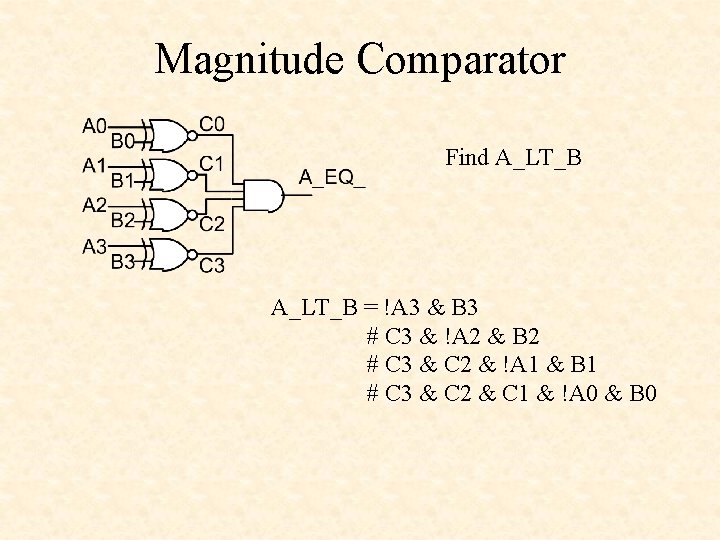
Magnitude Comparator Find A_LT_B = !A 3 & B 3 # C 3 & !A 2 & B 2 # C 3 & C 2 & !A 1 & B 1 # C 3 & C 2 & C 1 & !A 0 & B 0

Comparators • Equality and Magnitude Comparators – CSE 171 (Designed using CUPL) • TTL Comparators • Comparator Networks • Cascading 1 -bit Comparators – Design using VHDL - Lab 3

TTL Comparators 1 B 3 16 Vcc 2 A<Bin A 3 15 3 B 2 14 A=Bin 4 A>Bin A 2 13 5 12 A>Bout A 1 6 A=Bout B 1 11 7 A<Bout A 0 10 8 GND B 0 9 74 LS 85 1 P>Q 2 P 0 3 Q 0 4 P 1 5 Q 1 6 P 2 7 Q 2 8 P 3 9 Q 3 10 GND 20 Vcc P=Q 19 Q 7 18 17 P 7 Q 6 16 15 P 6 Q 5 14 P 5 13 Q 4 12 P 4 11 74 LS 682

Cascading two 74 LS 85 s

Comparators • Equality and Magnitude Comparators – CSE 171 (Designed using CUPL) • TTL Comparators • Comparator Networks • Cascading 1 -bit Comparators – Design using VHDL - Lab 3
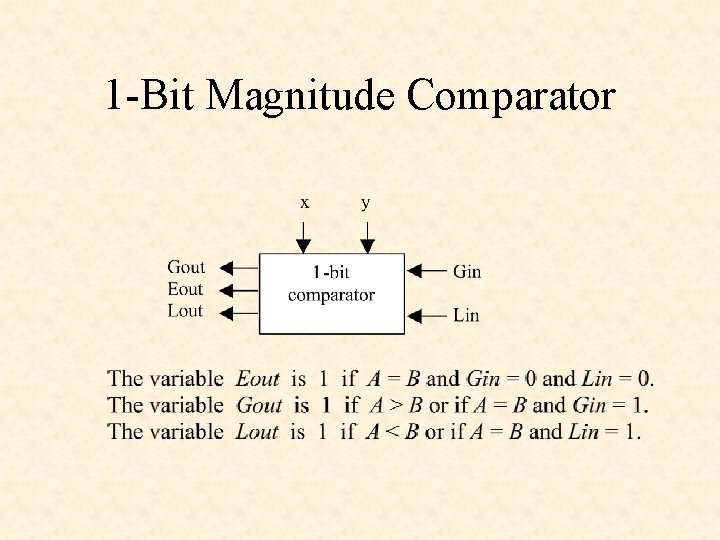
1 -Bit Magnitude Comparator
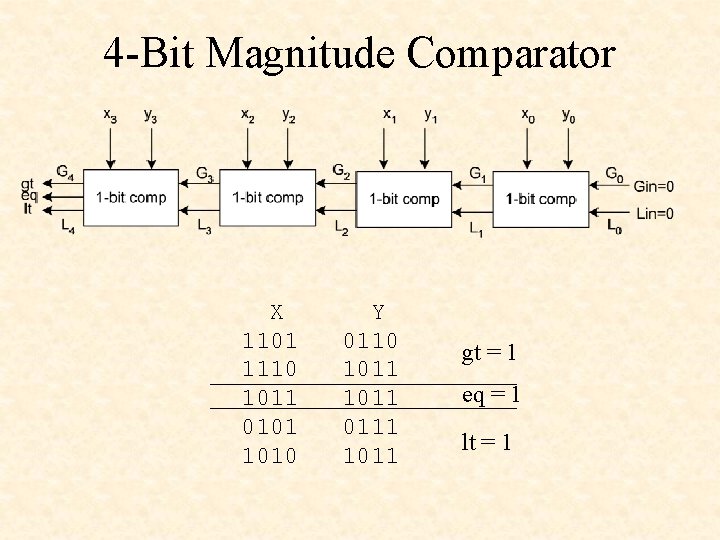
4 -Bit Magnitude Comparator X 1101 1110 1011 0101 1010 Y 0110 1011 0111 1011 gt = 1 eq = 1 lt = 1
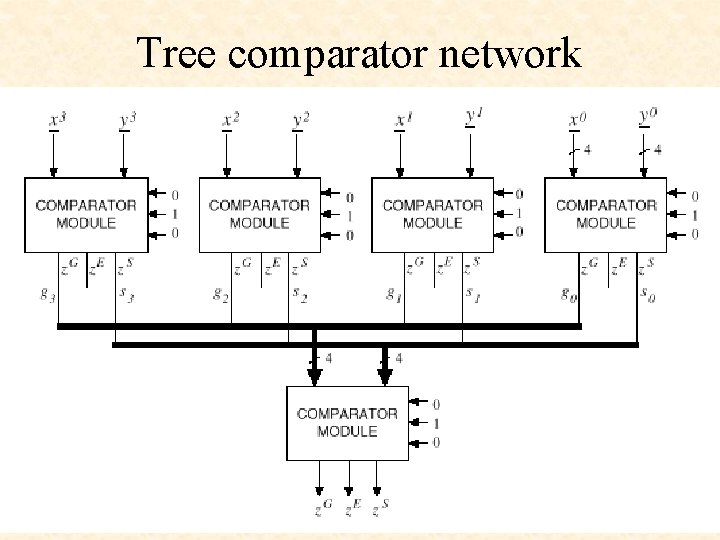
Tree comparator network

Comparators • Equality and Magnitude Comparators – CSE 171 (Designed using CUPL) • TTL Comparators • Comparator Networks • Comparator Design using VHDL

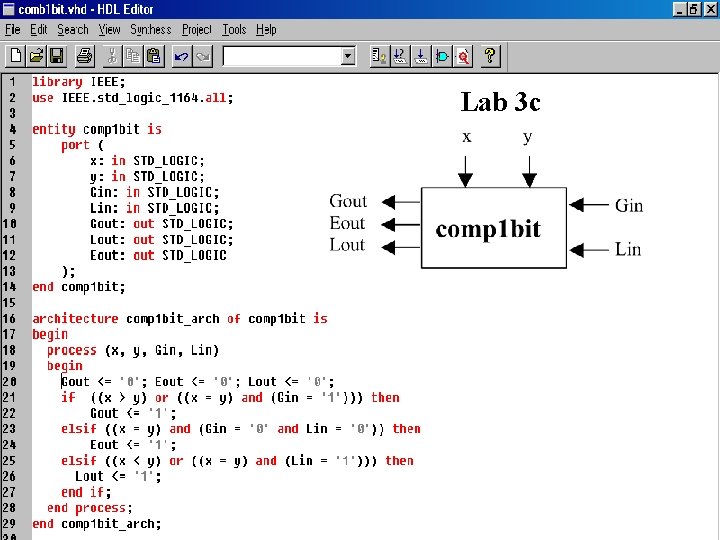
Lab 3 c
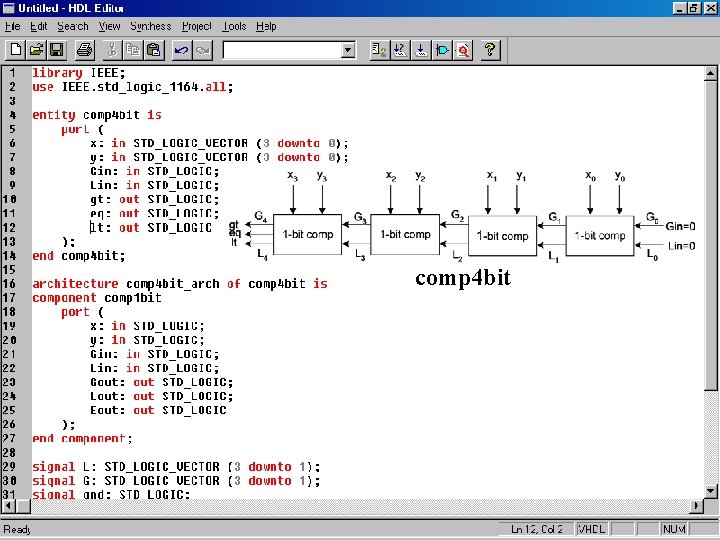
comp 4 bit
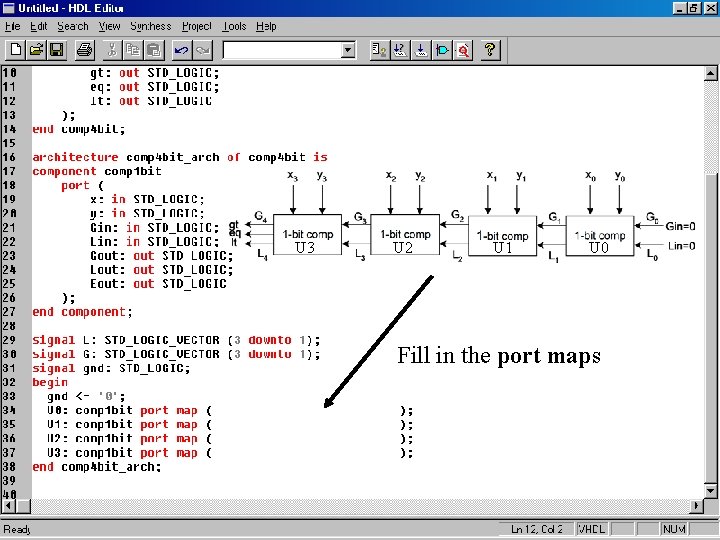
U 3 U 2 U 1 U 0 Fill in the port maps
- Slides: 25